Delta 1/2024

Klub 44

Marcin E. Kuczma i Elżbieta Zawistowska

Errata do wersji w druku: W rozwiązaniu zadania 762 w wyśrodkowanej równości po prawej stronie powinno być $3 \sqrt{p_{f}^{2} c^{2} / 9 + m^{2} c^{4}} .$

Zadania z matematyki nr 873, 874

Redaguje Marcin E. KUCZMA

873. Dany jest trójkąt ostrokątny $A B C .$ Niech $ℓ$ będzie dowolną prostą przecinającą boki $A B$ i $A C$ odpowiednio w takich punktach $P$ i $Q,$ że $∡ A C P + ∡ A P Q = 90^{\circ},$ i niech $X$ będzie rzutem prostokątnym punktu $C$ na prostą $ℓ .$ Udowodnić, że (dla ustalonego trójkąta $A B C$ ) wszystkie punkty $X,$ uzyskane w ten sposób przy różnych dopuszczalnych położeniach prostej $ℓ,$ leżą na jednej prostej.

874. Liczba $\sqrt{7}$ została zapisana w systemie dwójkowym jako $10, c_{1} c_{2} c_{3} \dots$ ; to znaczy $\sqrt{7} = 2^{1} + \sum_{i = 1}^{\infty} c_{i} 2^{- i},$ $c_{i} \in {0, 1} .$ Dowieść, że dla każdej liczby naturalnej $n \geq 1$ suma $\sum_{i = n}^{2 n} c_{i}$ jest dodatnia.

Zadanie 874 zaproponował pan Paweł Kubit z Krakowa.

Rozwiązania zadań z numeru 9/2023

Przypominamy treść zadań:

865. W czworokącie wypukłym $A B C D$ kąty przy wierzchołkach $A$ i $C$ są proste (ale nie przy wierzchołkach $B$ i $D$ ). Punkt $M$ jest środkiem przekątnej $A C .$ Punkt $E$ jest symetryczny do $B$ względem $M .$ Dowieść, że okręgi opisane na trójkątach $A B C$ i $A D E$ są przystające.

Rozwiązanie

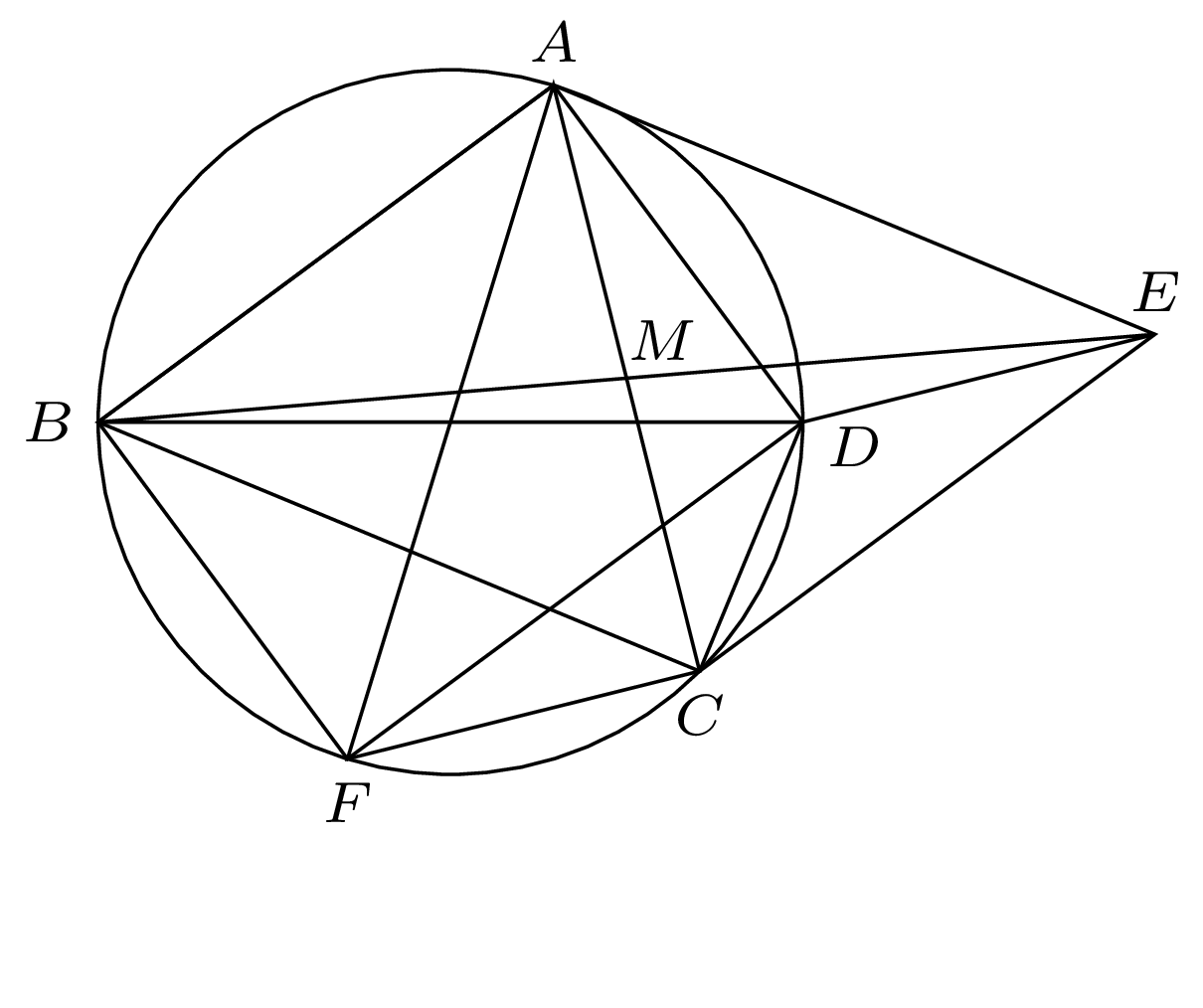
Punkty $A$ i $C$ leżą na okręgu o średnicy $B D .$ Niech $F$ będzie punktem antypodycznym do $A$ na tym okręgu; odcinek $A F$ też jest jego średnicą, więc czworokąt $A B F D$ jest prostokątem. Odcinki $A C$ i $B E$ mają wspólny środek $M,$ co oznacza, że czworokąt $A B C E$ jest równoległobokiem. Zatem $A E = B C,$ $A D = B F$ ; dostajemy też związki równoległości $A E ‖ B C$ oraz $A D ‖ B F .$ Wynika z nich, że $∡ D A E = ∡ F B C$ (punkty $C$ i $F$ nie pokrywają się, bowiem – z założenia – kąty $A B C$ i $C D A$ nie są proste; z tego samego powodu nie pokrywają się punkty $D$ i $E$ ).

Z uzyskanych zależności wnosimy, że trójkąty $D A E$ i $F B C$ są przystające; zatem i okręgi na nich opisane są przystające. Pozostaje zauważyć, że okrąg $F B C$ jest też opisany na trójkącie $A B C .$

866. Dane są dwie różne liczby pierwsze $p,$ $q$ takie, że $2^{p} - 1$ oraz $2^{q} - 1$ też są liczbami pierwszymi, a ponadto każda z liczb $2^{p - 1} - 1$ oraz $2^{q - 1} - 1$ dzieli się przez iloczyn $p q .$ Udowodnić, że jeżeli liczba całkowita dodatnia $d$ jest dzielnikiem liczby $2^{p q} - 1,$ to liczba $d - 1$ dzieli się przez $p q .$

Rozwiązanie

Rozważmy najpierw przypadek, gdy $d$ jest liczbą pierwszą (nieparzystą, skoro dzieli liczbę $2^{p q} - 1$ ). Niech $t$ będzie najmniejszą liczbą całkowitą dodatnią, dla której $2^{t} \equiv 1$ (mod $d$ ). Ponieważ (z założenia) $2^{p q} \equiv 1$ (mod $d$ ), zatem $p q$ dzieli się przez $t .$

Możliwe są trzy podprzypadki: $t = p q$ lub $t = p$ lub $t = q .$ W myśl małego twierdzenia Fermata $2^{d - 1} \equiv 1$ (mod $d$ ), zatem także wykładnik $d - 1$ dzieli się przez $t .$ W podprzypadku $t = p q$ jest to teza zadania.

W podprzypadku $t = p$ liczba $d$ jest dzielnikiem liczby $2^{p} - 1$ (która z założenia jest pierwsza); to znaczy, że $d = 2^{p} - 1 .$ Stąd $d - 1 = 2 (2^{p - 1} - 1) .$ To znów daje tezę, bo czynnik w nawiasie jest (z założenia) podzielny przez $p q .$ Dla $t = q$ rozumowanie biegnie tak samo.

Pozostaje przypadek ogólny – gdy $d = d_{1} \dots d_{n}$ (iloczyn liczb pierwszych, niekoniecznie różnych). Założenie $d ∣ 2^{p q} - 1$ implikuje, że $d_{i} ∣ 2^{p q} - 1$ dla wszystkich $i .$ Na mocy przypadku już rozpatrzonego: $d_{i} \equiv 1$ (mod $p q$ ) dla wszystkich $i .$ Stąd $d \equiv 1$ (mod $p q$ ) – czyli teza w przypadku ogólnym.

Zadania z fizyki nr 770, 771

Redaguje Elżbieta ZAWISTOWSKA

770. Z izolowanego cieplnie naczynia o objętości wewnętrznej $V$ odpompowano wypełniający je gaz, osiągając wysoką próżnię. Otaczające powietrze ma temperaturę $T_{0}$ i ciśnienie $p_{0} .$ W pewnym momencie otworzono kran zamykający naczynie, i nastąpiło jego szybkie napełnienie powietrzem atmosferycznym. Jaką temperaturę $T$ miało powietrze w naczyniu po jego napełnieniu i zamknięciu kranu? Powietrze traktujemy jako gaz doskonały, którego wykładnik adiabaty $γ = c_{p} / c_{V}$ jest dany, pojemności cieplnej ścianek naczynia nie uwzględniamy.

771. Cząstkę punktową o masie $m$ i ładunku $Q$ umieszczono w odległości $R$ od nieskończonej płaszczyzny przewodzącej i puszczono swobodnie. Po jakim czasie cząstka doleci do płaszczyzny? Siły ciężkości nie uwzględniamy.

Rozwiązania zadań z numeru 9/2023

Przypominamy treść zadań:

762. Przekształcenie fotonu w parę elektron–pozyton w próżni jest niemożliwe, ze względu na zasadę zachowania pędu. Znaleźć minimalną energię, jaką powinien posiadać foton, aby mogła powstać para elektron–pozyton w pobliżu spoczywającego elektronu.

Rozwiązanie

Rozważmy układ odniesienia, w którym spoczywa środek masy wszystkich trzech cząstek – wyjściowego elektronu i tworzącej się pary elektron–pozyton. W tym układzie energia całkowita będzie najmniejsza, jeśli wszystkie te cząstki będą spoczywały. W układzie laboratoryjnym odpowiada to sytuacji, gdy wszystkie cząstki po utworzeniu się pary mają jednakowe wektory prędkości. Masy cząstek są jednakowe, zatem jednakowe są też ich wektory pędu. Pęd fotonu przed powstaniem pary zostaje rozdzielony równo pomiędzy trzy cząstki w stanie końcowym: $p_{f} = 3 p,$ gdzie $p$ jest pędem każdej z nich. Z zasady zachowania energii: $p_{f} c + m c^{2} = 3 \sqrt{p_{f}^{2} c^{2} / 9 + m^{2} c^{4}},$ gdzie $m$ jest masą elektronu. Stąd szukana energia progowa fotonu wynosi $4 m c^{2} .$

763. Na poziomej powierzchni lodu narysowany jest okrąg o promieniu $R = 10$ m. W chwili początkowej zając Z znajduje się w środku okręgu, a wilk W na okręgu, jak na rysunku 1. Zając porusza się po prostej z prędkością $v_{0} = 2$ m/s. Wilk powinien poruszać się po okręgu tak, aby odległość między nim a zającem nie zmieniała się. Do jakiego punktu na okręgu uda mu się w ten sposób dotrzeć? Współczynnik tarcia wilka o lód: $μ = 0, 05.$ Wilk nie podskakuje.

Rozwiązanie

Załóżmy, że w pewnej chwili zając znajduje się w punkcie $A$ (rys. 2).

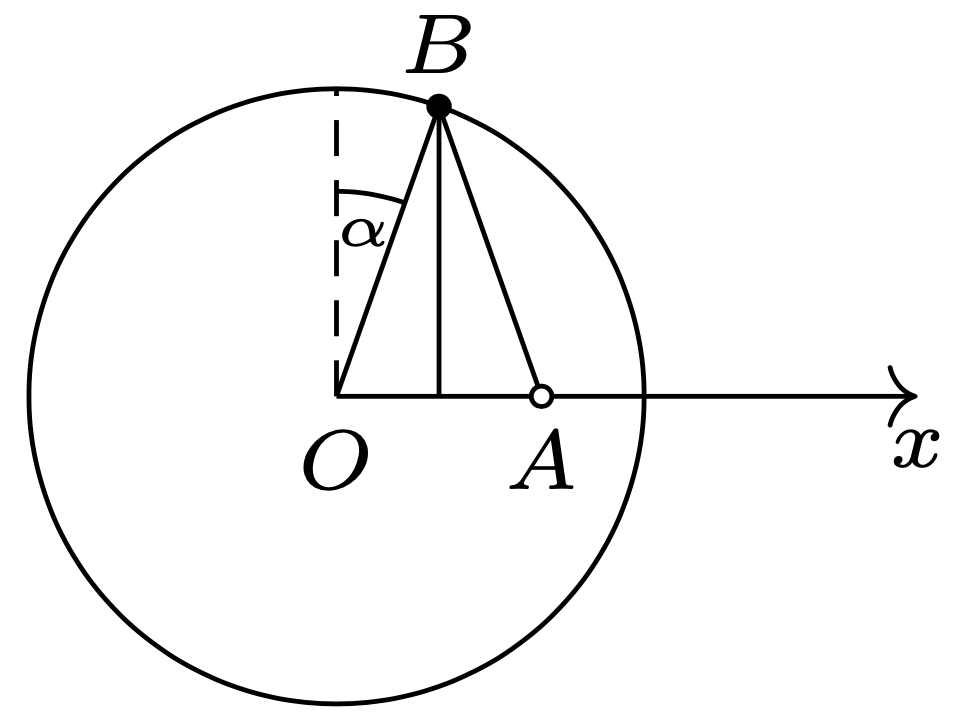Rys. 2

Zgodnie z treścią zadania wilk powinien znajdować się w tej chwili w punkcie $B$ – wierzchołku trójkąta równoramiennego $O A B .$ Wilk przemieszcza się w kierunku osi $O X$ ze stałą prędkością $v_{0} / 2,$ zatem jego przyspieszenie $a$ ma kierunek wysokości trójkąta $O A B,$ a jego prędkość wypadkowa jest styczna do okręgu i wynosi $V = (v_{0} / 2) \cos α .$ Przyspieszenie dośrodkowe $a_{d} = V^{2} / R = a \cos α,$ stąd $a = v_{0}^{2} / 4 R \cos^{3} α .$ Z drugiej strony $a = T / M \leq μ g,$ gdzie $M$ jest masą wilka, a $T$ siłą tarcia statycznego. Maksymalny kąt opisujący punkt na okręgu, do którego może dotrzeć wilk, określa równanie $\cos α_{0} = \sqrt[3]{v_{0}^{2} / 4 R μ g} \approx 0, 59,$ stąd $α_{0} \approx 54^{\circ} .$

Termin nadsyłania rozwiązań: 31 III 2024

Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
863 ( $W T = 2, 33$ ) i 864 ( $W T = 2, 40$ )
z numeru 6/2023

Krzysztof Maziarz Londyn 44,68

Radosław Kujawa Wrocław 43,57

Paweł Najman Kraków 43,16

Adam Woryna Ruda Śl. 40,91

Marek Spychała Warszawa 40,20

Janusz Fiett Warszawa 39,62

Jerzy Cisło Wrocław 37,70

Paweł Kubit Kraków 36,11

Szymon Tur 35,35

Piotr Kumor Olsztyn 35,26

Pan Krzysztof Maziarz (niegdyś z Jasła, potem z Krakowa, teraz z Londynu) zgromadził był do końca roku 2021 saldo 40,67p., po czym się chwilowo z nami rozstał; jego nazwisko wkrótce znikło z publikowanej czołówki. Ale oto wrócił – i od razu zgrabnym ruchem przeskoczył 44 p., dołączając tym samym do matematycznego Klubu 44.

Termin nadsyłania rozwiązań: 31 III 2024

Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
760 ( $W T = 2, 6$ ), 761 ( $W T = 1, 83$ )
z numeru 6/2023

Tomasz Rudny Poznań 43,41

Marian Łupieżowiec Gliwice 2–40,56

Jacek Konieczny Poznań 38,28

Tomasz Wietecha Tarnów 16–37,54

Konrad Kapcia Poznań 2–35,60

Ryszard Baniewicz Włocławek 1–29,40

Andrzej Nowogrodzki Chocianów 3–20,97

Paweł Perkowski Ożarów Maz. 5–20,95

Rys. 1

Krzysztof Maziarz	Londyn	44,68
Radosław Kujawa	Wrocław	43,57
Paweł Najman	Kraków	43,16
Adam Woryna	Ruda Śl.	40,91
Marek Spychała	Warszawa	40,20
Janusz Fiett	Warszawa	39,62
Jerzy Cisło	Wrocław	37,70
Paweł Kubit	Kraków	36,11
Szymon Tur		35,35
Piotr Kumor	Olsztyn	35,26

Tomasz Rudny	Poznań	43,41
Marian Łupieżowiec	Gliwice	2–40,56
Jacek Konieczny	Poznań	38,28
Tomasz Wietecha	Tarnów	16–37,54
Konrad Kapcia	Poznań	2–35,60
Ryszard Baniewicz	Włocławek	1–29,40
Andrzej Nowogrodzki	Chocianów	3–20,97
Paweł Perkowski	Ożarów Maz.	5–20,95