Delta 3/2024

Zadania

Dominik Burek i Andrzej Majhofer

matematyka

Przygotował Dominik BUREK

Zadanie M 1774

Każda liczba ciągu $a_{1}, a_{2}, a_{3}, \dots, a_{2 n}, a_{2 n + 1}$ jest równa $2,$ $5$ lub $9.$ Ponadto $a_{1} = a_{2 n + 1}$ oraz dowolne dwa sąsiednie wyrazy tego ciągu są różne. Udowodnić, że $a_{1} a_{2} - a_{2} a_{3} + a_{3} a_{4} - \dots + a_{2 n - 1} a_{2 n} - a_{2 n} a_{2 n + 1} = 0.$

Rozwiązanie

Ponieważ każda liczba w ciągu

a_{1}, a_{2}, a_{3}, \dots, a_{2 n}, a_{2 n + 1}

przyjmuje jedną z trzech wartości, a dowolne dwie sąsiednie liczby są różne, wobec tego dowolny składnik rozważanego w zadaniu wyrażenia

a_{1} a_{2} - a_{2} a_{3} + \dots + a_{2 n - 1} a_{2 n} - a_{2 n} a_{2 n + 1}

przyjmuje również (co do modułu) jedną z trzech wartości.

Wystarczy zatem pokazać, że każda wartość w danym wyrażeniu pojawia się tyle samo razy ze znakiem $+,$ co ze znakiem $- .$ Zauważmy jednak, że każda z wartości 2, 5, 9, odpowiednio, występuje w zbiorach par ${(a_{1}, a_{2}), (a_{3}, a_{4}), \dots, (a_{2 n - 1}, a_{2 n})}$ oraz ${(a_{2}, a_{3}), (a_{4}, a_{5}), \dots, (a_{2 n}, a_{2 n + 1})}$ tyle samo razy, oznaczmy te liczby wystąpień odpowiednio przez $k,$ $l$ i $m .$ Wtedy oczywiście $k + l + m = 2 n .$ Wobec tego w każdym zbiorze par liczba par $5, 9$ jest równa dokładnie $\frac{- k + l + m}{2},$ liczba par $2, 9$ jest równa $\frac{k - l + m}{2},$ a liczba par $2, 5$ jest równa $\frac{k + l - m}{2} .$

Zadanie M 1775

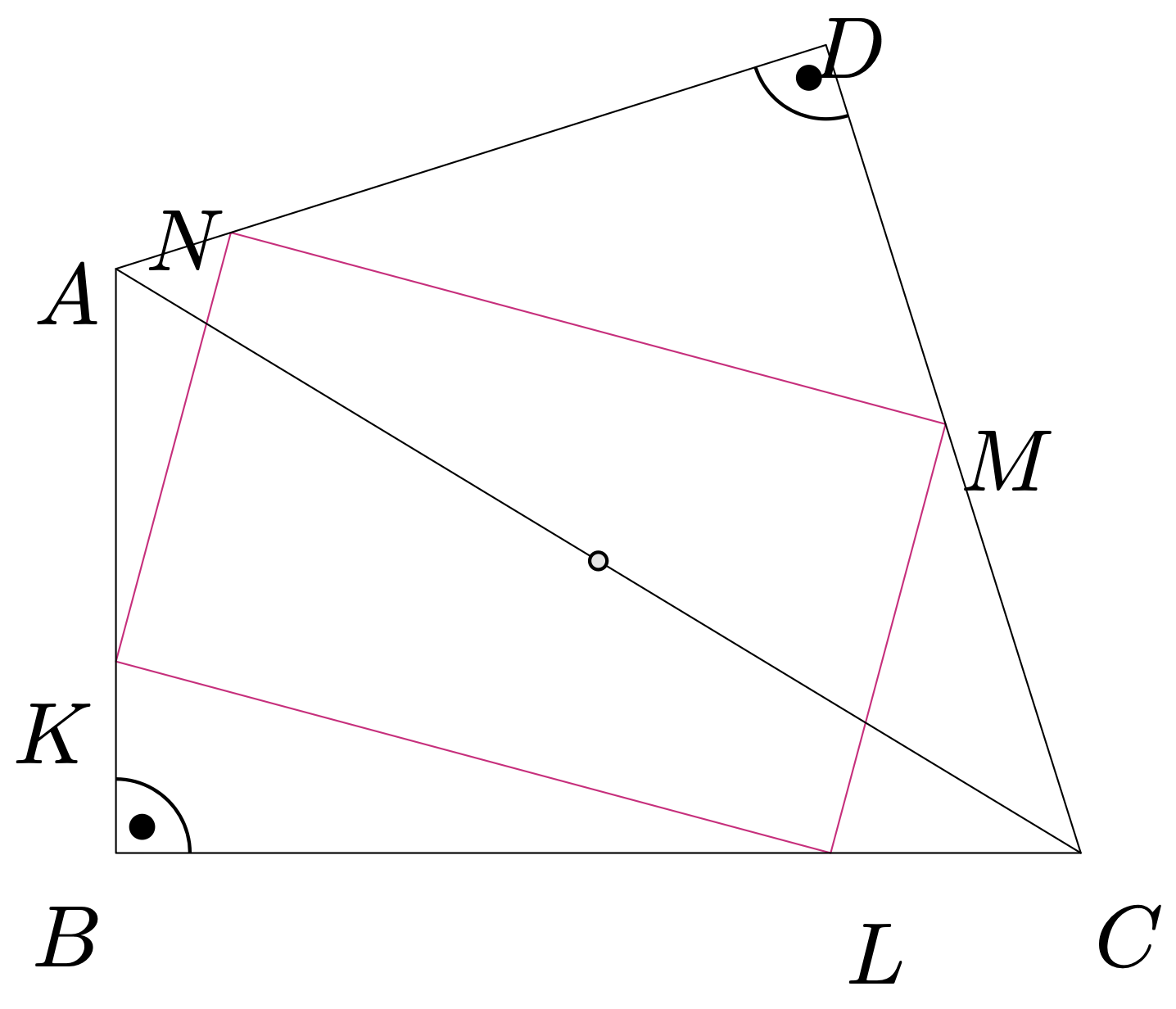
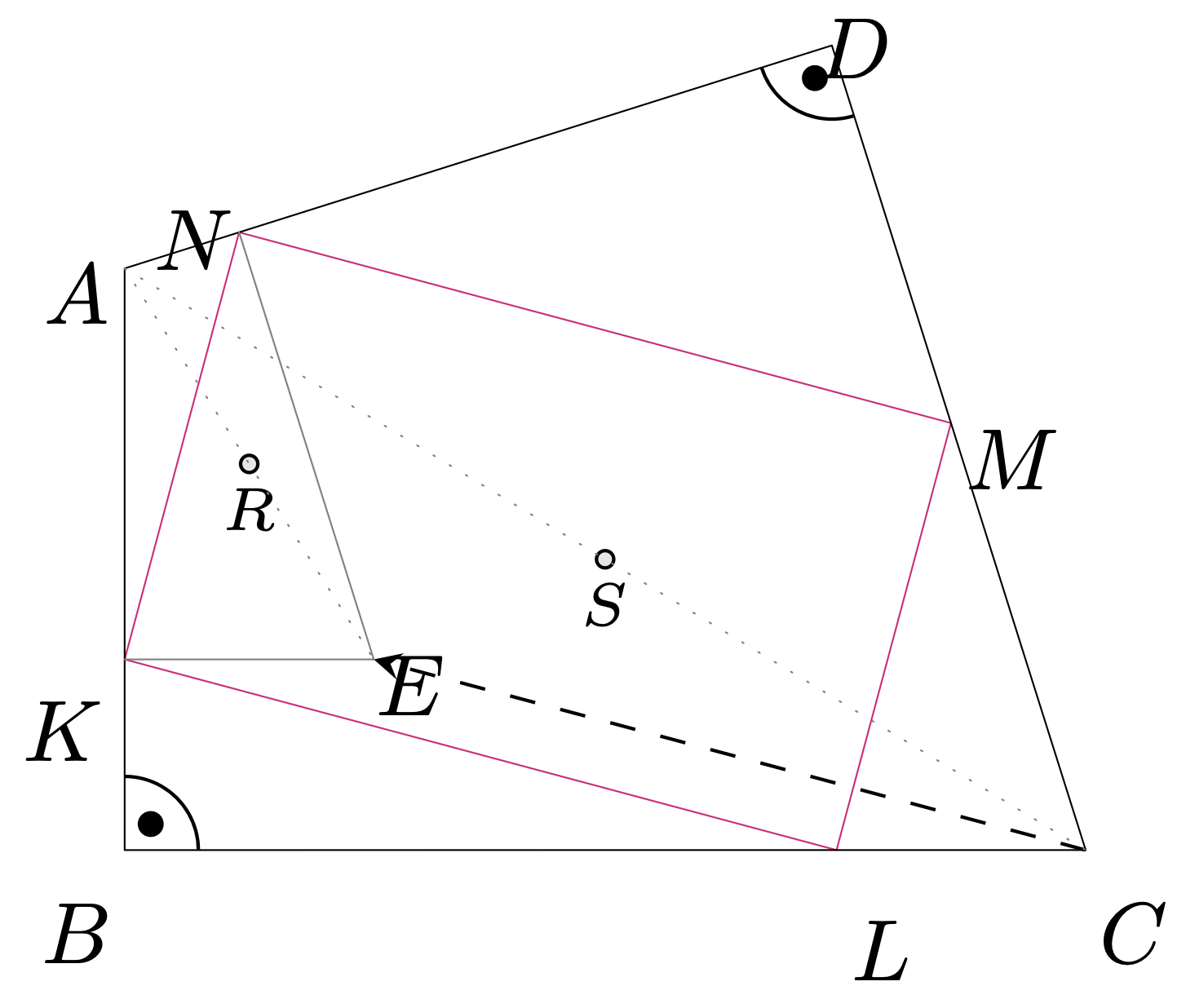
W wypukłym czworokącie $A B C D$ kąty $A B C$ i $A D C$ są proste. Punkty $K,$ $L,$ $M,$ $N$ leżą odpowiednio na bokach $A B,$ $B C,$ $C D,$ $D A,$ przy czym czworokąt $K L M N$ jest prostokątem. Udowodnić, że środek przekątnej $A C$ jest równoodległy od prostych $K L$ i $M N .$

Rozwiązanie

Przesuńmy równolegle trójkąt

L M C

o wektor

\vec{L K} = \vec{M N},

otrzymując trójkąt

K N E .

Ponieważ

C L ⊥ A K,

E K ⊥ A K .

Podobnie

E N ⊥ A N .

Zauważmy, że środek

R

odcinka

A E

jest środkiem okręgu opisanego na czworokącie

A K E N,

zatem

R

leży na symetralnej odcinka

K N .

Niech $S$ będzie środkiem przekątnej $A C .$ Wtedy $R S ∥ E C ∥ K L,$ co oznacza, że $R S ⊥ K N,$ a zatem $S$ również leży na symetralnej odcinka $K N$ – co oczywiście implikuje tezę.

Zadanie M 1776

Dane są liczby rzeczywiste $a, b, c$ takie, że $| \frac{a^{2} + b^{2} - c^{2}}{a b} | < 2.$ Udowodnić, że $| \frac{b^{2} + c^{2} - a^{2}}{b c} | < 2 oraz | \frac{c^{2} + a^{2} - b^{2}}{c a} | < 2.$

Rozwiązanie

Zauważmy, że mnożenie dowolnej liczby

a,

b,

c

przez

- 1

nie zmienia prawdziwości żadnej z rozważanych nierówności. Ponadto

a b \neq 0.

Oznacza to, że bez straty ogólności możemy założyć, że

a > 0, b > 0

oraz

c \geq 0.

Zapisując pierwszą z nierówności jako $| \frac{a^{2} + b^{2} - c^{2}}{2 a b} | < 1,$ widzimy, że istnieje liczba $γ \in (0, π),$ spełniająca równość $c^{2} = a^{2} + b^{2} - 2 a b \cos γ .$

Skonstruujmy trójkąt $T,$ którego dwa boki są równe $a$ i $b,$ a kąt między tymi bokami jest równy $γ .$ Niech trzeci bok tego trójkąta będzie równy $c_{1} .$ Na podstawie twierdzenia cosinusów zastosowanego dla trójkąta $T$ dostajemy równość $c_{1}^{2} = a^{2} + b^{2} - 2 a b \cos γ = c^{2},$ więc $c = c_{1} .$ Niech $α,$ $β$ będą kątami między bokami $b,$ $c$ oraz $c,$ $a$ trójkąta $T .$ Ponownie, korzystając z twierdzenia cosinusów, dostajemy $\begin{aligned} | \frac{b^{2} + c^{2} - a^{2}}{b c} | & = 2 | \cos α | oraz \\ | \frac{c^{2} + a^{2} - b^{2}}{c a} | & = 2 | \cos β |, \end{aligned}$ więc nierówności z tezy są oczywiście spełnione.

Przygotował Andrzej MAJHOFER

Zadanie F 1091

Na sąsiednich, równoległych torach ustawiono tramwaj zasilany z zewnętrznej sieci elektrycznej oraz elektrowóz zasilany ze znajdujących się w nim akumulatorów i rozpoczęto ,,wyścig”. W chwili startu masy obu pojazdów były równe i wynosiły $m_{0} = 4, 2 \cdot 10^{4}$ kg. Po pewnym czasie oba pojazdy osiągnęły prędkość $v$ równą 4/5 prędkości światła $c .$ Jakie masy miały w tym momencie oba pojazdy w układzie odniesienia związanym z torami?

Rozwiązanie

Po osiągnięciu prędkości

v = 0, 8 c

masa tramwaju wynosiła

m_{1} = \frac{m_{0}}{\sqrt{1 - v^{2}}} = \frac{10}{6} m_{0},

tzn.

m_{1} = 7 \cdot 10^{4}

kg, a masa elektrowozu

m_{2} = m_{0} = 4, 2 \cdot 10^{4}

kg. Tramwaj zwiększał swoją energię kinetyczną, a więc i całkowitą masę, dzięki pobieraniu energii z zewnątrz (z sieci elektrycznej). Elektrowóz natomiast rozpędzał się, zamieniając w energię kinetyczną energię potencjalną zgromadzoną w będących jego częścią akumulatorach, a zatem jego całkowita energia (i równoważna jej masa) nie uległa zmianie podczas rozpędzania.

Zadanie F 1092

Obraz tarczy słonecznej otrzymany przy pomocy kulistego zwierciadła wklęsłego o promieniu $r = 10$ cm i ogniskowej $f = 1$ m pada na cienki krążek o rozmiarach identycznych z rozmiarami obrazu Słońca, wykonany z matowego materiału absorbującego światło. Oszacuj, do jakiej maksymalnej temperatury $T$ można w ten sposób ogrzać krążek, jeśli temperatura powierzchni Słońca wynosi $T_{0} \approx 6000$ K? Wpływ efektów związanych z aberracją sferyczną należy pominąć.

Rozwiązanie

Na potrzeby naszego oszacowania potraktujemy Słońce i krążek jak ciała doskonale czarne wypromieniowujące energię zgodnie ze wzorem (prawo Stefana–Boltzmanna):

P = σ T^{4} S,

w którym

P

oznacza całkowitą moc promieniowania,

S

powierzchnię ciała, a

T

temperaturę powierzchni w skali Kelwina. Wprowadźmy oznaczenia:

R_{S}

– promień Słońca,

R

– odległość zwierciadła od Słońca i

δ

– promień krążka (i obrazu Słońca). Moc promieniowania słonecznego docierającego do powierzchni zwierciadła wynosi:

P_{Z} = 4 π R_{S}^{2} σ T_{0}^{4} \frac{π r^{2}}{4 π R^{2}} .

Przyjmijmy dalej, że zwierciadło odbija doskonale, i cała moc

P_{Z}

,,trafia” w krążek. Temperatura

T

krążka ustali się, gdy moc promieniowania z jego powierzchni (promieniują obie strony cienkiego krążka) będzie równa

P_{Z}

P_{Z} = 2 π δ^{2} σ T^{4} .

Otrzymujemy związek:

\frac{R_{S}^{2}}{R^{2}} T_{0}^{4} = \frac{2 δ^{2}}{r^{2}} T^{4} .

Ze względu na ogromną odległość Słońca od zwierciadła jego obraz powstaje praktycznie w ognisku zwierciadła. Przyrównując stosunki rozmiarów przedmiotu

R_{s}

i obrazu

δ

do stosunków ich odległości od powierzchni zwierciadła, mamy

R_{S} / R = δ / f

i ostatecznie:

{(\frac{T}{T_{0}})}^{4} = \frac{r^{2}}{2 f^{2}} .

Po podstawieniu danych liczbowych:

T \approx 1600