Afiliacja: Doktorantka, Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Rewolucja! W królestwie Bajtocji wynaleziono telefon, i młody król, który właśnie zasiadł na tronie, chce wykorzystać ten wspaniały wynalazek do usprawnienia komunikacji w swoim królestwie. Dawniej każdą wiadomość przenosił gołąb pocztowy, a jak powszechnie wiadomo, jest to system dość wolny i zawodny. Król zarządził zatem zainstalowanie telefonu w każdym mieście. Kiedy jednak jego doradcy pokazali mu kosztorys projektu, król złapał się za głowę i zdecydował na inne rozwiązanie: aparaty mają być zainstalowane w taki sposób, by wszyscy poddani mieli dostęp do telefonu w swoim mieście lub w pewnym innym mieście połączonym bezpośrednio drogą z ich miastem. Doradcy króla głowią się teraz, w których miastach je zainstalować, tak aby było ich jak najmniej i tym samym koszt projektu był jak najniższy.
Przedstawmy nasz problem w języku teorii grafów. Rozważmy graf \(G=(V,E),\) w którym zbiór wierzchołków \(V\) reprezentuje miasta w królestwie, a zbiór krawędzi \(E\) odpowiada istniejącym połączeniom drogowym. Chcemy znaleźć taki podzbiór wierzchołków \(D,\) by każdy wierzchołek grafu albo sam należał do zbioru \(D,\) albo miał sąsiada w zbiorze \(D.\) Każdy wierzchołek o takiej własności nazwiemy zdominowanym. W opisanej sytuacji zdominowane są wszystkie wierzchołki, podzbiór \(D\) nazwiemy więc zbiorem dominującym. Oczywiście, wybierając \(D=V,\) wskażemy poprawny zbiór dominujący, ale, podobnie jak króla, interesuje nas zbiór o możliwie najmniejszej liczbie wierzchołków.
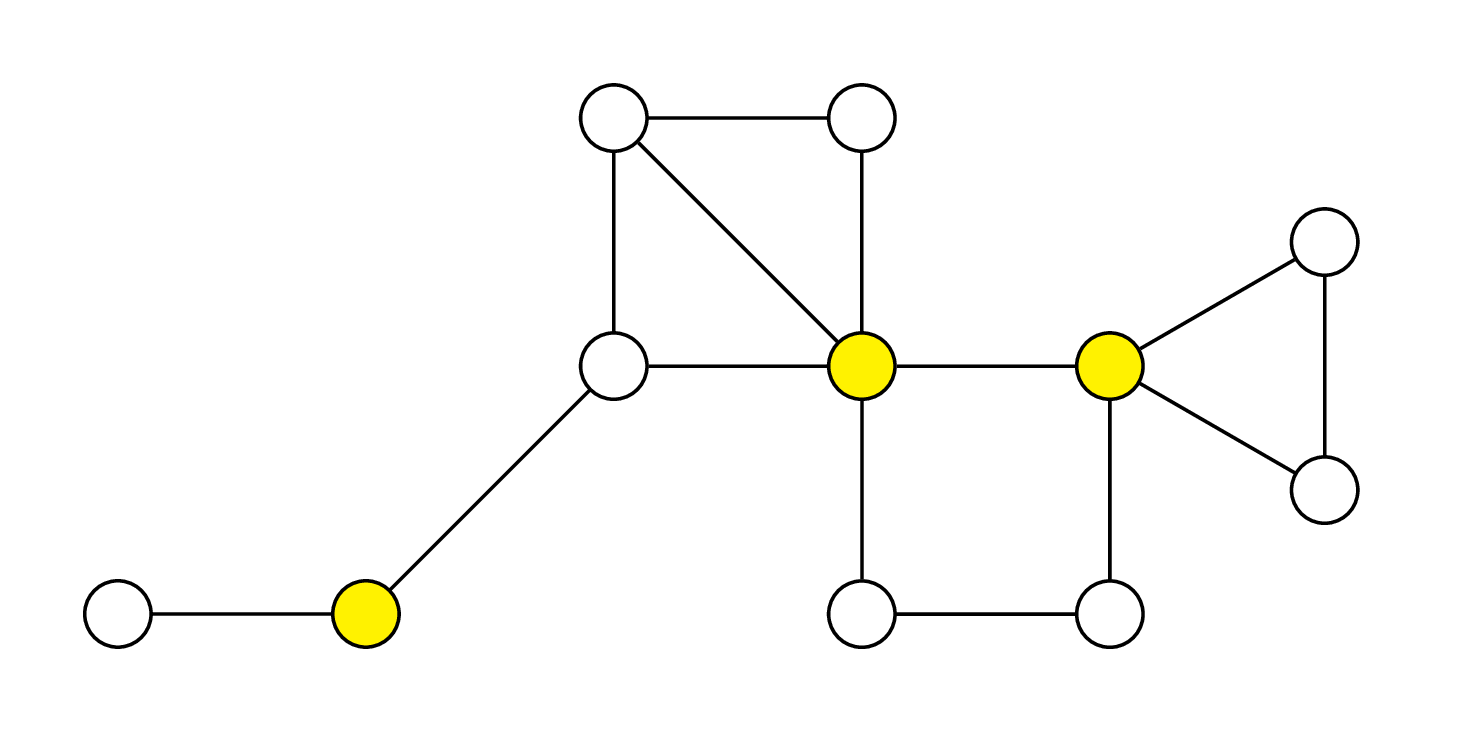
Na rysunku zaznaczono żółtym kolorem wierzchołki należące do zbioru dominującego
Opisany problem w teorii grafów nosi nazwę problemu minimalnego zbioru dominującego. Możemy także rozważyć wariant, gdy koszty wybudowania telefonu w poszczególnych miastach się różnią – każdemu miastu \(v_i\) przypisujemy koszt \(c(v_i),\) który będziemy też nazywać wagą. Naszym zadaniem jest wtedy wskazanie zbioru dominującego o minimalnej sumarycznej wadze. Jest to wówczas problem zbioru dominującego o minimalnej wadze.
Naturalnym pomysłem w przypadku tego typu problemów jest podejście zachłanne, w którym zaczynamy od pustego zbioru \(D\) i kolejno dodajemy do niego wierzchołki, które wydają się najbardziej przybliżać nas do celu. Powiedzmy, że jesteśmy w trakcie takiej procedury, i przez \(Z\) oznaczmy zbiór wierzchołków zdominowanych, czyli należących w danym momencie do zbioru \(D\) (który na koniec tej procedury będzie zbiorem dominującym), lub posiadających sąsiada w zbiorze \(D.\) Początkowo zbiór \(Z\) jest pusty. W każdym kroku wybieramy wierzchołek, który nie należy do zbioru \(Z\) i ma największą liczbę sąsiadów nienależących do zbioru \(Z.\) Taki wierzchołek dodajemy do zbioru \(D\) – wtedy on i wszyscy jego sąsiedzi trafiają do zbioru \(Z.\) Postępujemy w ten sposób, dopóki wszystkie wierzchołki \(G\) nie zostaną włączone do \(Z.\) Wydawałoby się, że takie podejście to dobry pomysł, jako że w każdym kroku zwiększamy \(Z\) o maksymalną w tym momencie liczbę wierzchołków. Istnieją jednak grafy, dla których to podejście nie jest optymalne:
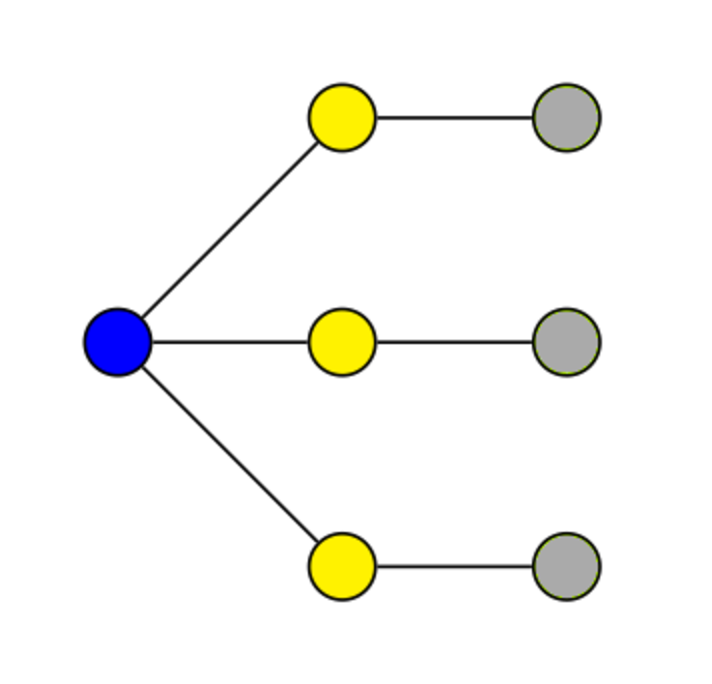
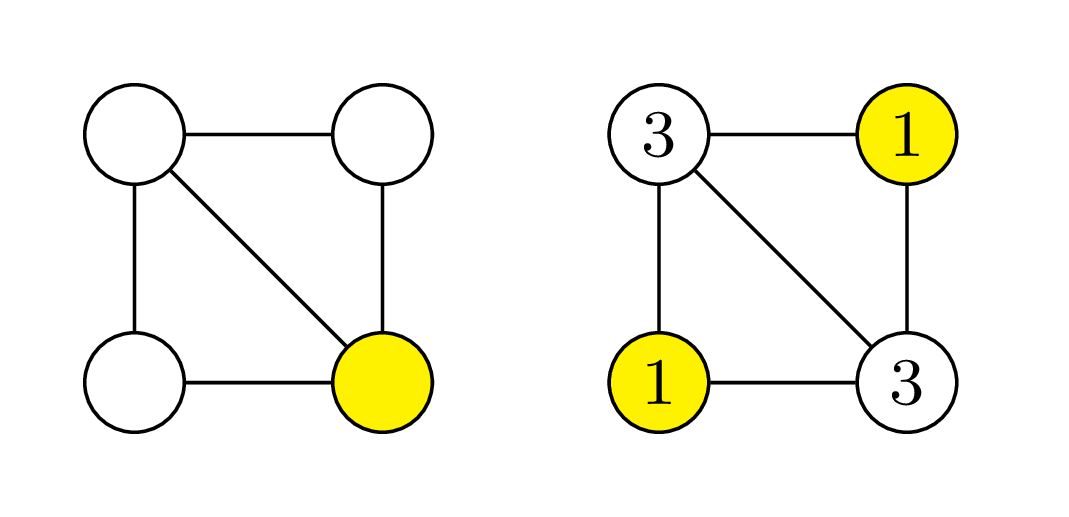
W powyższym przykładzie najpierw włączymy do grafu niebieski wierzchołek. Wtedy żółte wierzchołki zostaną zdominowane. W kolejnych krokach nasz algorytm włoży wszystkie trzy szare wierzchołki do zbioru dominującego. W ten sposób otrzymamy zbiór dominujący o mocy \(4.\) Zauważmy jednak, że zbiór żółtych wierzchołków jest poprawnym zbiorem dominującym o mocy \(3.\)
Na rysunku zaznaczono na żółto wierzchołki grafu należące do zbioru dominującego. Zauważmy, że w przypadku problemu ważonego czasami opłaca nam się wybrać więcej wierzchołków niż w przypadku grafu bez wag
Obydwa opisane problemy możemy rozwiązać, rozważając wszystkie możliwe podzbiory wierzchołków grafu, sprawdzając, które z nich są zbiorami dominującymi, i wybierając najmniejszy z nich. Złożoność czasowa tego algorytmu to \(\mathcal{O}(2^{|V|}\cdot |E|),\) co zdecydowanie nie jest satysfakcjonujące (dla grafu o zaledwie 20 wierzchołkach \(2^{|V|} \cdot |E|\) może być równe prawie 200 milionów!). Czy jesteśmy w stanie zaproponować zatem szybsze, tj. wielomianowe rozwiązanie? Nie spodziewamy się, by odpowiedź była pozytywna – obydwa te problemy są NP-trudne. Z drugiej strony potrzebujemy umieć szybko i efektywnie rozwiązywać to zadanie, ponieważ występuje w wielu rzeczywistych scenariuszach związanych z dystrybucją zasobów.
W dużym uproszczeniu, problemy NP-trudne to takie problemy, dla których nie znamy algorytmów działających w czasie wielomianowym i mamy dobre powody, aby sądzić, że takie algorytmy nie istnieją.
Jednym ze sposobów radzenia sobie z NP-trudnymi problemami grafowymi jest uważne przyjrzenie się grafom, dla których potrzebujemy znaleźć rozwiązanie – być może mają one dodatkowe przydatne własności. Przykładowo wiemy, że w grafie miast połączonych drogami bez mostów, tuneli ani skrzyżowań nie można znaleźć pięciu miast połączonych każde z każdym (korzystamy tutaj z twierdzenia Kuratowskiego charakteryzującego grafy planarne).
Znając lepiej własności grafów, dla których mamy rozwiązywać nasz problem, możemy projektować algorytmy korzystające z tych własności i działające szybciej niż algorytm rozwiązujący nasz problem dla dowolnego grafu.
Przypadek ścieżki
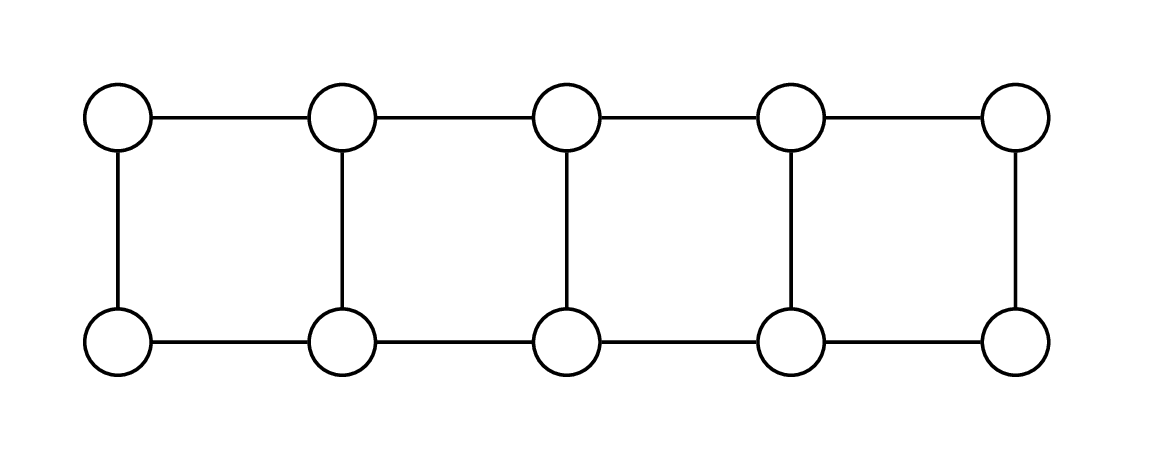
Rozważmy graf, który jest ścieżką (patrz rysunek na marginesie). Oznaczmy jego kolejne wierzchołki przez \(v_1,\) \(v_2,\) \(\dots,\) \(v_n.\) Jak rozwiązać zagadnienie minimalnego zbioru dominującego dla ścieżek? Jeżeli wierzchołki nie mają wag, możemy po prostu wybrać co trzeci wierzchołek, zaczynając od drugiego wierzchołka ścieżki.
Na żółto zaznaczono wierzchołki należące do minimalnego zbioru dominującego
W przypadku ważonym nasze zadanie się nieco komplikuje, ale nadal istnieje algorytm liniowy znajdujący optymalne rozwiązanie. Dla każdego \(i \in \{1,2, \dots, n\}\) rozważmy optymalny zbiór dominujący dla ścieżki złożonej z wierzchołków \(v_1-v_2-\dots-v_i\) w każdym z trzech scenariuszy:
wierzchołek \(v_i\) należy do zbioru dominującego;
\(v_i\) nie należy do zbioru dominującego, ale jego sąsiad \(v_{i-1}\) już tak;
zarówno \(v_i,\) jak i \(v_{i-1}\) nie należą do zbioru dominującego (zauważmy, że w tym przypadku wierzchołek \(v_i\) nie jest zdominowany).
Oznaczmy optymalny zbiór dominujący dla ścieżki \(v_1-v_2-\dots -v_i\) dla każdego z trzech wyżej opisanych przypadków jako, odpowiednio, \(D_i^1, D_i^2, D_i^3,\) a przez \(k(D_i^j)\) oznaczmy sumaryczny koszt wierzchołków w zbiorze \(D_i^j.\) Zauważmy, że jeśli mamy już znalezione optymalne zbiory dla \(i\) w każdym scenariuszu, możemy łatwo znaleźć wyniki dla \(i+1.\)
Niech \(j=\arg \min_{j=1,2,3}\ k(D_i^j).\) Wtedy \(D_{i+1}^1 = D_i^j \cup \{v_{i+1}\}.\)
Z definicji zachodzi \(D_{i+1}^2 = D_i^1.\)
W ostatnim scenariuszu wierzchołki \(v_i\) i \(v_{i+1}\) nie należą do zbioru dominującego, zatem wierzchołek \(v_i\) musi być zdominowany przez wierzchołek \(v_{i-1}.\) Zatem zachodzi \(D_{i+1}^3 = D_i^2.\)
Aby znaleźć najlepsze rozwiązanie dla całej ścieżki, wybieramy rozwiązanie o mniejszej sumarycznej wadze dla \(i=n\) spośród pierwszych dwóch scenariuszy (w ostatnim wierzchołek \(v_n\) nie byłby dominowany). Dopracowanie szczegółów i dowód poprawności algorytmu pozostawiamy Czytelnikowi.
Szerokość ścieżkowa
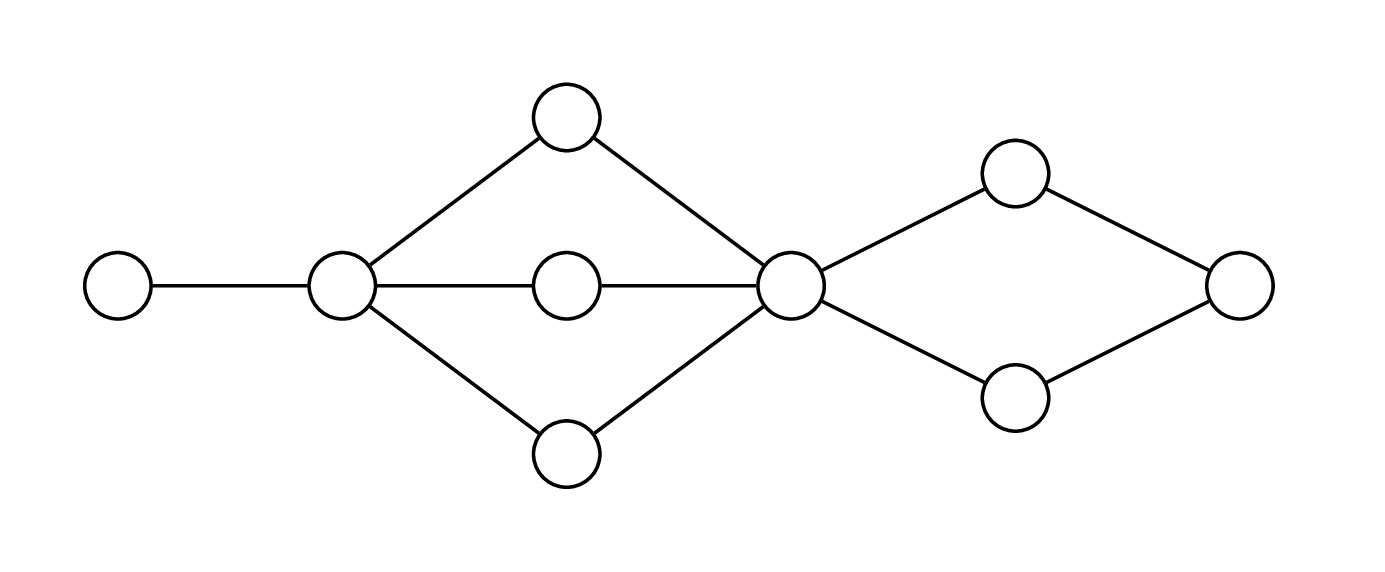
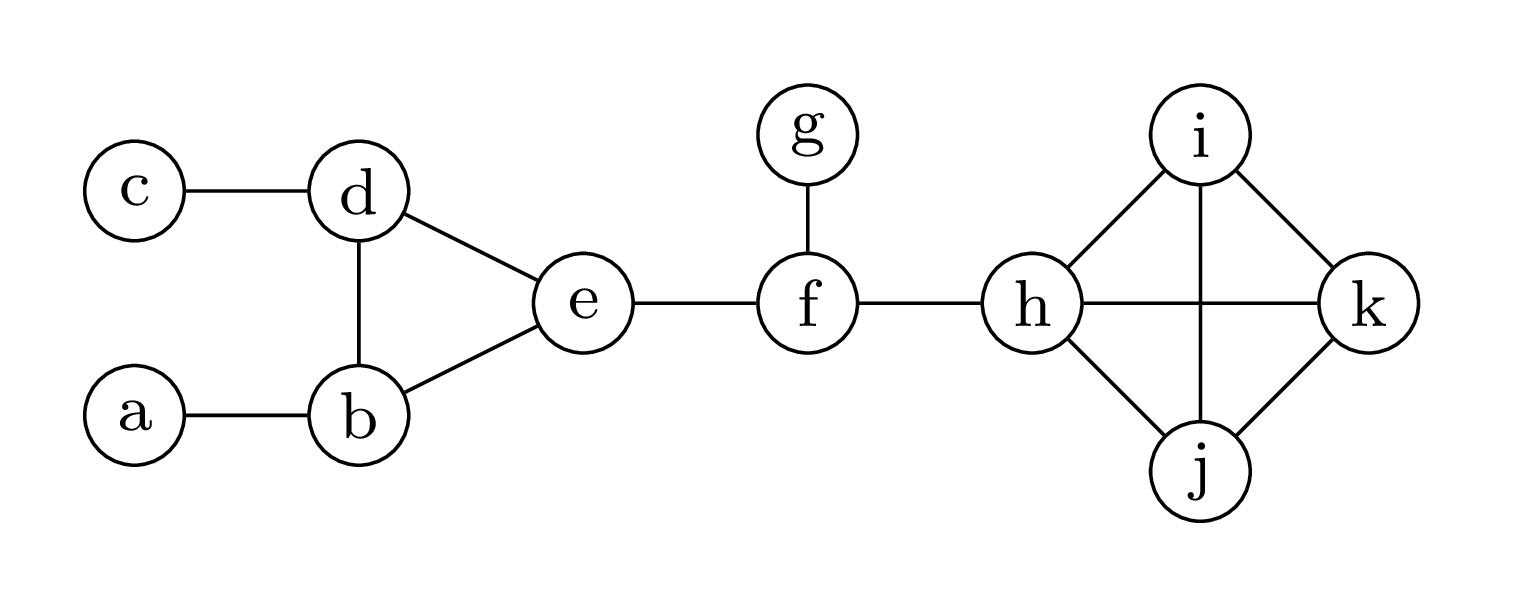
Dla ogólnych grafów nie możemy niestety skorzystać z tego algorytmu, bo wierzchołki mogą być ze sobą połączone w znacznie bardziej skomplikowany sposób. Rodzi się jednak pytanie, co w przypadku, gdy rozważany graf jest podobny do ścieżki (np. tak jak grafy przedstawione na obrazkach na marginesie). Może potrafilibyśmy wykorzystać nasze zrozumienie problemu dla ścieżek do skonstruowania algorytmu dla grafów przypominających ścieżki?
Zanim pójdziemy dalej, musimy sformalizować pojęcie podobieństwa do ścieżki. Dekompozycją ścieżkową (ang. path decomposition) grafu \(G\) nazywamy parę \((P, \{\beta(u)\}_{u\in V(P)}),\) gdzie \(P\) jest ścieżką, a każdemu wierzchołkowi \(u\) przyporządkowany jest zbiór \(\beta(u)\subseteq V(G)\) (zwany workiem) tak, że spełnione są następujące dwa warunki:
Graf i jego dekompozycja ścieżkowa o szerokości \(3\)
dla każdych dwóch wierzchołków \(v_1\) i \(v_2\) połączonych krawędzią w grafie \(G\) istnieje wierzchołek \(u\in V(P),\) którego worek zawiera \(v_1\) i \(v_2\);
dla każdego wierzchołka \(v\) grafu \(G\) zbiór wierzchołków \(P,\) których worki zawierają \(v,\) tworzy niepusty, spójny podgraf \(P\) (czyli w tym przypadku ścieżkę).
Szerokość dekompozycji ścieżkowej \((P, \{\beta(u)\}_{u\in V(P)})\) to \(\max_{u\in V(P)} |\beta(u)|-1.\) Szerokością ścieżkową (ang. pathwidth) grafu \(G\) nazywamy minimalną możliwą szerokość dekompozycji ścieżkowej grafu \(G.\) W definicji odejmujemy \(1,\) by ścieżki miały szerokość ścieżkową równą \(1,\) a nie \(2.\)
Okazuje się, że szerokość ścieżkowa wielu grafów rozważanych w rzeczywistych scenariuszach jest mała (czyli ograniczona przez pewną stałą). Jest to bardzo wygodne, gdyż możemy wykorzystać tę własność do projektowania szybkich algorytmów.
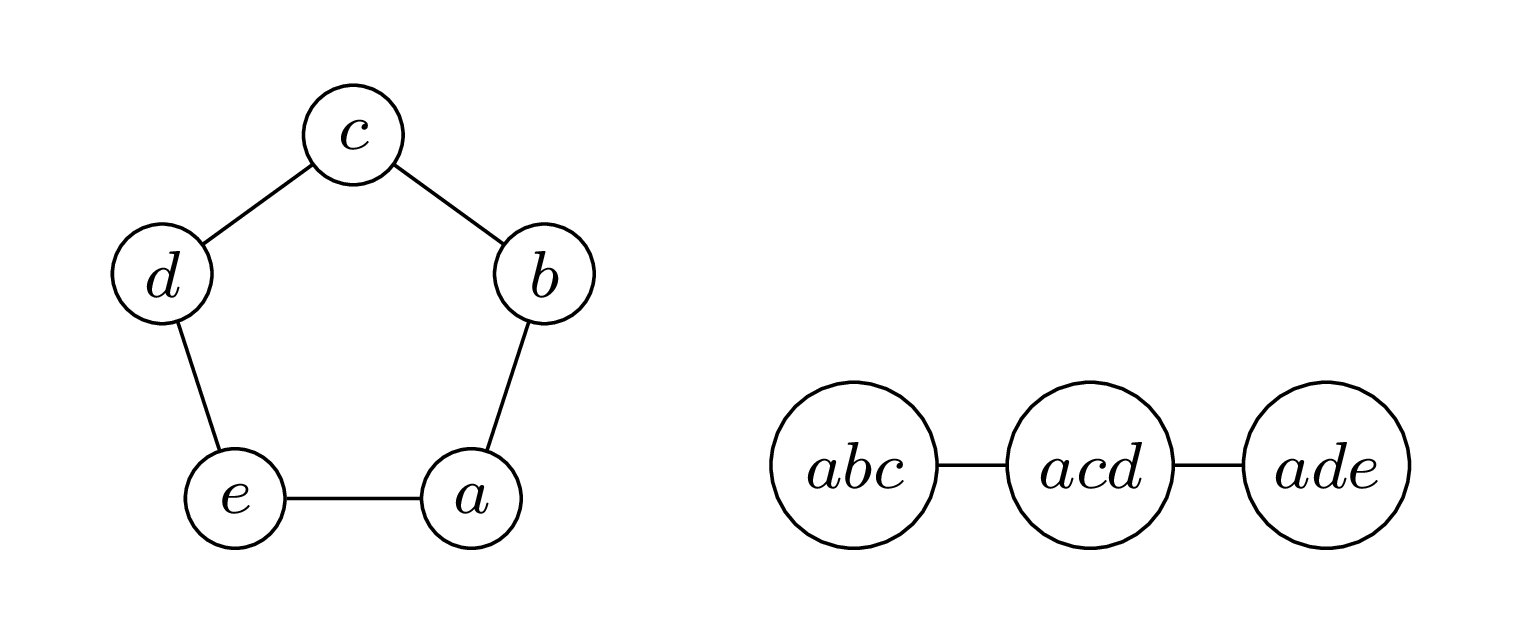
Każdy cykl ma szerokość ścieżkową równą \(2\) – dla każdego możemy zaproponować dekompozycję analogiczną do tej na obrazku (tutaj dla cyklu o długości \(5\)). Z drugiej strony ścieżki mają szerokość ścieżkową równą \(1\)
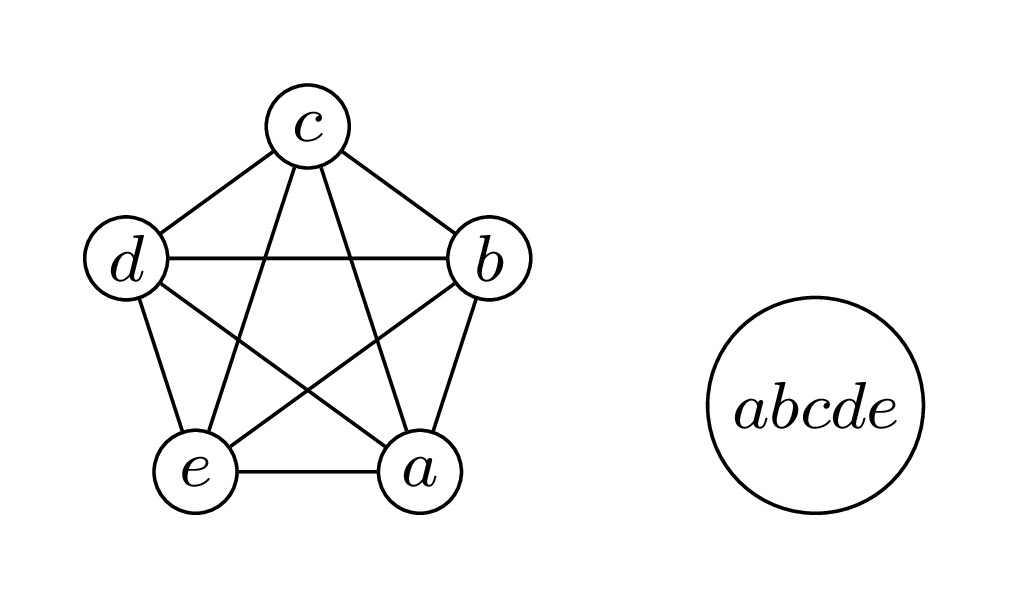
Można udowodnić, że dla grafu będącego kliką musi istnieć worek zawierający wszystkie wierzchołki. Zatem klika o \(n\) wierzchołkach ma szerokość ścieżkową równą \(n-1\)
W dalszej części artykułu skoncentrujemy się na problemie najmniejszego zbioru dominującego w grafie bez wag. Algorytm, który podamy, można łatwo zmodyfikować, aby działał również w przypadku grafów z wagami, jednak pominiemy te szczegóły, aby idea algorytmu była bardziej przejrzysta.
Gdy konstruowaliśmy zbiór dominujący o minimalnej wadze dla ścieżki, w momencie \(i+1\) nie potrzebowaliśmy wiedzieć, jak wygląda cały optymalny zbiór dominujący dla ścieżki złożonej z pierwszych \(i\) wierzchołków – korzystaliśmy jedynie z wiedzy o wierzchołkach \(v_{i-1}\) oraz \(v_i.\) Wykorzystamy teraz podobną intuicję, konstruując algorytm dynamiczny, który będzie działać dla grafów o ustalonej szerokości ścieżkowej – będziemy pamiętać minimalny koszt zbioru dominującego dla różnych możliwych stanów wierzchołków należących do obecnie rozważanego worka.
Rozważmy graf \(G\) i jego dekompozycję ścieżkową \((P, \{\beta(u)\}_{u\in V(P)}),\) gdzie \(P\) jest ścieżką \(u_1 - u_2-\dots-u_p.\) Przez \(k_i\) oznaczmy \(|\beta(u_i)|,\) a przez \(k = \max_{i=1,\dots, n} k_i\) oznaczmy szerokość ścieżkową \(P\) powiększoną o \(1.\) Dla każdego wierzchołka \(v\) grafu \(G\) rozróżniamy jeden z trzech możliwych stanów:
Czytelnikowi pozostawiamy jako zadanie pokazanie, że dowolną dekompozycję ścieżkową grafu o \(n\) wierzchołkach, która ma więcej niż \(2n\) worków, da się prosto skrócić do długości \(2n\) bez zwiększania jej szerokości, a więc możemy zakładać \(p \le 2n.\)
\(v\) należy do zbioru dominującego;
\(v\) nie należy do zbioru dominującego, ale jest zdominowany przez co najmniej jednego ze swoich sąsiadów;
\(v\) nie należy do zbioru dominującego i nie jest zdominowany przez żadnego ze swoich sąsiadów.
Będziemy konstruować najmniejszy zbiór dominujący, tak jak poprzednio, rozważając kolejne wierzchołki \(P\) wraz z przypisanymi im workami. Dla worka \(i\) rozważamy wszystkie możliwe konfiguracje stanów jego wierzchołków. Jest ich \(3^{k_i}\) – każdą konfigurację możemy reprezentować przez wektor \(\alpha = (s_1,s_2, \dots, s_{k_i}),\) gdzie \(s_j\in \{1,2,3\}\) dla \(j\in \{1,\dots, k_i\)}. Rodzinę wszystkich możliwych wektorów stanów worka \(\beta(u_i)\) oznaczymy jako \(\mathcal{S}_i.\)
Najpierw generujemy (czyli rozpatrujemy) wszystkie możliwe stany dla pierwszego worka \(\beta(u_1).\) Przez \(c(\alpha)\) dla \(\alpha\in\mathcal{S}_1\) oznaczmy liczbę wierzchołków, które przy stanie \(\alpha\) należą do zbioru dominującego. Może się jednak zdarzyć, że wektor \(\alpha\) reprezentuje niepoprawną konfigurację, np. gdy istnieje wierzchołek w stanie \(2,\) którego żaden sąsiad nie należy do zbioru dominującego (żaden nie jest w stanie \(1\)). Niepoprawnym wektorom \(\alpha\) przypisujemy \(c(\alpha)=\infty.\) To pozwala nam zainicjować algorytm programowania dynamicznego.
Załóżmy teraz, że dla każdego wektora \(\alpha\in\mathcal{S}_i\) mamy obliczony \(c(\alpha)\) – rozmiar minimalnego zbioru dominującego w grafie indukowanym przez wierzchołki należące do \(\beta(u_1)\cup\beta(u_2)\cup\dots\cup \beta(u_i),\) który zgadza się ze stanami opisanymi wektorem \(\alpha\) (jeśli taki zbiór dominujący nie istnieje albo gdy konfiguracja jest niepoprawna, to bierzemy \(c(\alpha)=\infty\)).
Chcielibyśmy teraz obliczyć wyniki dla stanów należących do \(\mathcal{S}_{i+1}.\) Przedtem przejrzymy jednak jeszcze raz nasze wyniki dla \(\mathcal{S}_i.\) Popatrzmy na wierzchołki należące do \(\beta(u_i),\) ale nienależące do \(\beta(u_{i+1}).\) Z własności dekompozycji ścieżkowej wiemy, że nie mają one sąsiadów w \({\beta(u_{i+1})\cup \beta(u_{i+2})\cup\dots \cup \beta(u_p)}\) poza tymi znajdującymi się już w \({ \beta(u_1)\cup\beta(u_2)\cup\ldots\cup\beta(u_i)}.\) W związku z tym każdy taki wierzchołek musi już należeć do zbioru dominującego albo być zdominowany, jako że w kolejnych krokach nie będziemy rozważali ich żadnych ,,nowych” sąsiadów. Zatem każdemu wektorowi \(\alpha,\) w którym jeden z wierzchołków ze zbioru \(\beta(u_i) \setminus \beta(u_{i+1})\) jest w stanie \(3,\) przypisujemy \(c(\alpha)=\infty.\)
Teraz możemy w końcu dodać nowe wierzchołki. Rozważmy wszystkie możliwe konfiguracje wierzchołków należących do \(\beta(u_i)\) poszerzone o konfiguracje wierzchołków z \(\beta(u_{i+1})\setminus \beta(u_i).\) Możemy wtedy obliczyć wartość \(c\) dla takich rozszerzonych konfiguracji: w przypadku konfiguracji poprawnych zwiększając wartość o liczbę wierzchołków, którym przypisano stan \(1,\) a w przypadku konfiguracji niepoprawnych utrzymując przypisanie \(\infty.\) Zauważmy teraz, że jeśli zapomnimy we wszystkich konfiguracjach o wierzchołkach należących do \(\beta(u_i),\) ale nienależących do \(\beta(u_{i+1}),\) to otrzymamy zbiór wszystkich konfiguracji \(\mathcal{S}_{i+1}\) wraz z obliczonymi dla nich wartościami funkcji \(c.\)
Obliczamy w ten sposób wyniki dla kolejnych \({i=2,3, \dots, p}.\) Aby znaleźć minimalny wynik dla całego grafu \(G,\) rozważamy wszystkie poprawne konfiguracje dla \(\beta(u_p),\) w których każdy wierzchołek jest w stanie 1 lub 2, i wybieramy tę, dla której wartość funkcji \(c\) jest najmniejsza. Znaleźliśmy zatem liczność minimalnego zbioru dominującego. Jaka jest złożoność czasowa naszego algorytmu? Każdy krok, czyli wygenerowanie wszystkich stanów dla worka oraz sprawdzenie ich poprawności, wykonujemy w czasie \(\mathcal{O}(3^k).\) Wykonamy \(p \le 2n\) kroków – tyle, ile wynosi długość ścieżki \(P.\) Nasz algorytm działa zatem w czasie \(\mathcal{O}(n\cdot 3^k).\) Dla grafów o małej szerokości ścieżkowej jest to zatem znacznie lepszy czas niż opisany na początku algorytm działający w czasie \(\mathcal{O}(2^{|V|}|E|)\) (dla grafów o \(20\) wierzchołkach i gdy \(k=5,\) liczba \(n \cdot 3^k\) nie przekracza 5 tysięcy).
Opisana tutaj metoda ma też zastosowanie dla innych problemów NP-trudnych, w których szukamy algorytmów dynamicznych na dekompozycji ścieżkowej. W połączeniu z algorytmem obliczającym prawie optymalną dekompozycję ścieżkową (jest niestety dość skomplikowany, przez co musimy go pominąć) jesteśmy w stanie skonstruować algorytmy działające w czasie wielomianowym dla grafów o szerokości ścieżkowej ograniczonej przez stałą.
Okazuje się również, że grafy o małej szerokości ścieżkowej pojawiają się w prawdziwym życiu. Przykładowo, w przetwarzaniu języka naturalnego zdania można modelować jako grafy, gdzie wierzchołki odpowiadają pojedynczym słowom, zaś krawędź oznacza jakiś rodzaj zależności między słowami (np. przymiotnik modyfikujący znaczenie rzeczownika). Eksperymenty pokazują, że takie grafy mają na ogół niską szerokość ścieżkową – lingwiści twierdzą, że gdyby przekraczała ona \(6,\) to ludzie mieliby problem z rozumieniem mowy.
Na koniec dodajmy, że szerokość ścieżkowa została zaproponowana przez Neila Robertsona i Paula Seymoura w ich słynnym cyklu artykułów zatytułowanych Graph Minors. Prawdziwą rewolucją na salonach okazał się jednak inny, wprowadzony przez nich parametr uogólniający szerokość ścieżkową: szerokość drzewiasta. To jednak temat na kolejny artykuł.