Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Wiele algorytmów sortowania działa w ten sposób, że pary elementów na kolejno wskazanych miejscach są porównywane i jeśli drugi element z pary powinien poprzedzać pierwszy, przestawiane. Urządzenie lub procedurę porządkującą w ten sposób parę elementów nazywamy komparatorem.
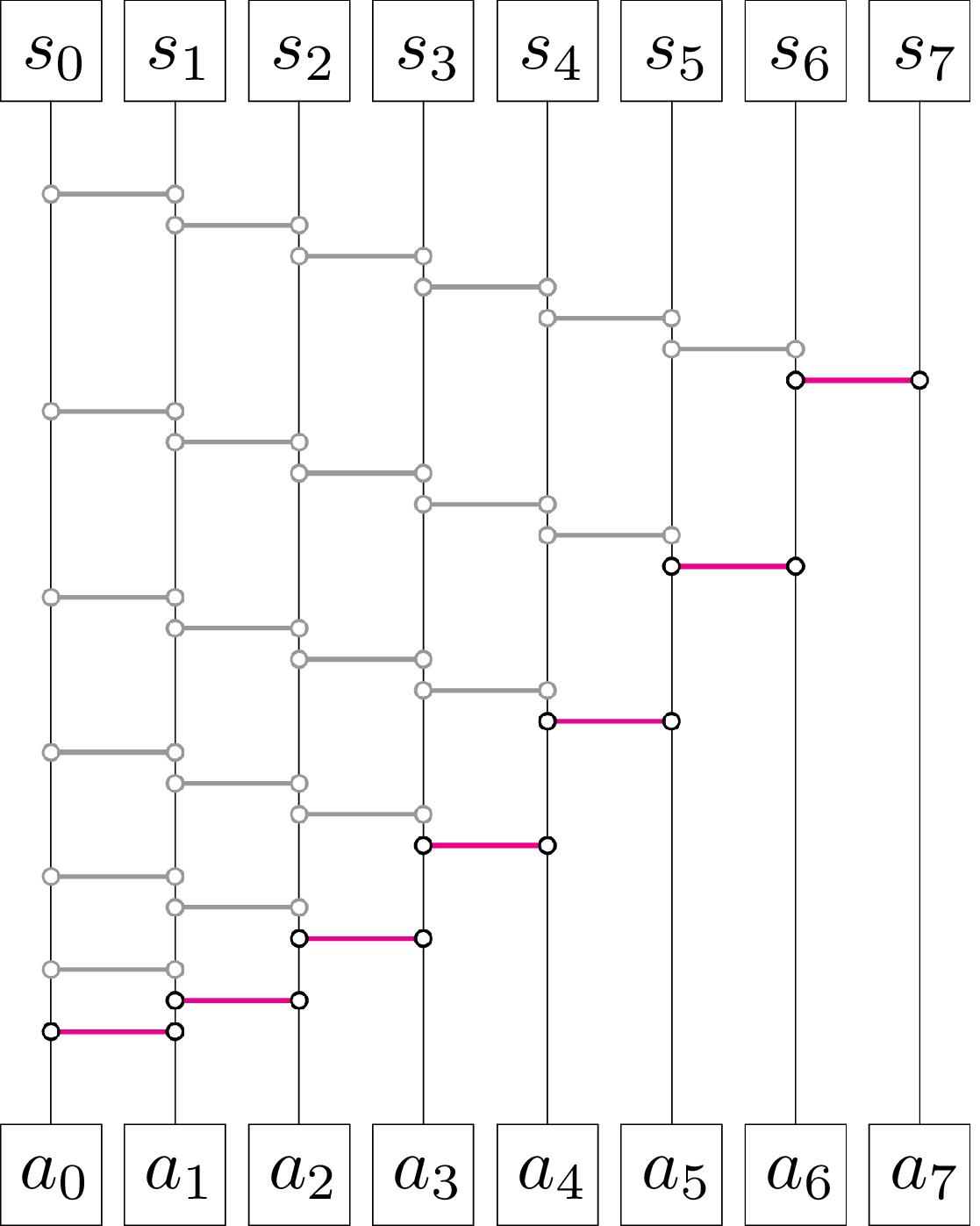
Rys. 1. Sieć sortująca algorytmu sortowania przez wstawianie. Na dole znajduje się ciąg dany, a na górze – posortowany
W niektórych algorytmach kolejność porównywanych par jest z góry ustalona, w związku z czym wynik porównania może spowodować co najwyżej pominięcie użycia komparatora dla pewnych dalszych par. Takie algorytmy możemy zilustrować za pomocą tzw. sieci sortującej. Rysunek 1 przedstawia taką sieć dla popularnego algorytmu sortowania przez wstawianie (Insertion sort). Sam algorytm jest następujący: kolejne elementy ciągu są ,,przesuwane w lewo”, dopóki nie napotkają elementu mniejszego od siebie (lub trafią na początek ciągu). W naszej ilustracji pionowe kreski symbolizują miejsca w sortowanej tablicy, a poziome kreski przedstawiają wywołania komparatora (w kolejności od dołu do góry), przy czym kolorem szarym są zaznaczone wywołania pomijane, gdy poprzednie wywołanie komparatora nie spowodowało przestawienia elementów. Liczba kolorowych kresek jest optymistyczną złożonością czasową tego algorytmu, a liczba wszystkich możliwych wywołań komparatora to złożoność pesymistyczna. Dla ciągu o długości \(n\) ta pierwsza złożoność to \(n-1,\) a ta druga jest równa \(\frac{1}{2}(n^2-n).\)
W algorytmach sekwencyjnych w danej chwili działa co najwyżej jeden komparator. Najszybsze algorytmy sekwencyjne mają złożoność pesymistyczną rzędu \(n\log n\) (choć nie da się ich tak pięknie zilustrować, jako że porównania i przestawiania są osobnymi operacjami i można w nich przestawiać inne elementy niż te, które właśnie zostały porównane). Mając natomiast do dyspozycji \(h=\lfloor\frac{n}{2}\rfloor\) wątków obliczeniowych, z których każdy wywoła komparator w tej samej chwili, można jednocześnie uporządkować \(h\) par elementów. Wykorzystuje to algorytm sortujący ciąg w czasie rzędu \(\log^2n.\) Można go zaimplementować na karcie graficznej, której kilkanaście tysięcy lub skromne kilkaset procesorów szybko posortuje nawet bardzo długi ciąg. Działanie algorytmu objaśnimy, pokazując sortowanie ciągów złożonych tylko z zer i jedynek. Takie podejście jest usprawiedliwione przez:
Twierdzenie. Dowolny algorytm sortowania przy użyciu sieci komparatorów, poprawnie sortujący wszystkie ciągi o długości \(n\) składające się z zer i jedynek, poprawnie sortuje też ciągi \(n\) elementów dowolnego zbioru liniowo uporządkowanego.
Dowód tego twierdzenia, zwanego zasadą zerojedynkową, jest podany w książce [1]. Ważny w dowodzie jest fakt, że jeśli drugi element z pary porządkowanej przez komparator nie jest mniejszy niż pierwszy (czyli w szczególności jeśli elementy są równe), to te elementy nie są przestawiane.
Zanim przedstawimy zapowiedziany algorytm sortowania, przyjmijmy jeszcze następujące definicje: ciągiem bitonicznym nazwiemy ciąg będący połączeniem dwóch ciągów monotonicznych: niemalejącego, po którym następuje nierosnący (mówimy o ciągu typu rm) albo nierosnącego, po którym następuje niemalejący (to jest ciąg typu mr). Dowolny ciąg monotoniczny (a w szczególności ciąg jednoelementowy) jest ciągiem bitonicznym obu tych typów.
Zauważmy, że ciąg zer i jedynek typu rm ma wszystkie jedynki skupione obok siebie, więc zera mogą występować tylko na jego początku i na końcu, a w ciągu typu mr wszystkie zera znajdują się obok siebie. Przyjrzymy się zatem porządkowaniu ciągów bitonicznych zer i jedynek.
Na zerojedynkowych ciągach bitonicznych długości \(2h\) będziemy przeprowadzać następującą operację: dzielimy je na dwie części równej długości i każemy komparatorom porządkować (jednocześnie) pary złożone z \(i\)-tych elementów każdej z połówek. Przykłady zastosowania tej operacji przedstawione są na rysunku 2; wyniki takiego porządkowania są pokazane nad każdym ciągiem. Możemy zauważyć, że w każdym przypadku powstają dwa ciągi bitoniczne o długości \(h,\) przy czym jeśli liczba zer nie przekracza \(h,\) to wszystkie zera znajdą się w pierwszym z nich, a w przeciwnym przypadku wszystkie jedynki trafią do drugiej połowy tablicy z elementami ciągu. Nietrudne uzasadnienie słuszności tej obserwacji dla dowolnego ciągu bitonicznego pozostawiam Czytelnikowi. Podkreślmy raz jeszcze, że mając do dyspozycji \(h\) wątków obliczeniowych, przedstawioną operację możemy wykonać w jednym kroku.
Powyższe spostrzeżenia pozwalają skonstruować oparty na komparatorach algorytm sortujący zerojedynkowe ciągi bitoniczne długości \(2^k\) w \(k\) krokach (jeśli mamy do dyspozycji \(2^{k-1}\) wątków obliczeniowych). Pierwszy krok został przedstawiony powyżej, w drugim kroku zajmujemy się każdym z dwóch powstałych ciągów bitonicznych z osobna (na każdy przeznaczając \(2^{k-2}\) wątków), w trzecim kroku mamy do czynienia z czterema ciągami bitonicznymi, i tak dalej… W ostatnim kroku etapu powstają bitoniczne ciągi o długości \(1\) i wtedy cały ciąg o długości \(2^k\) jest posortowany.
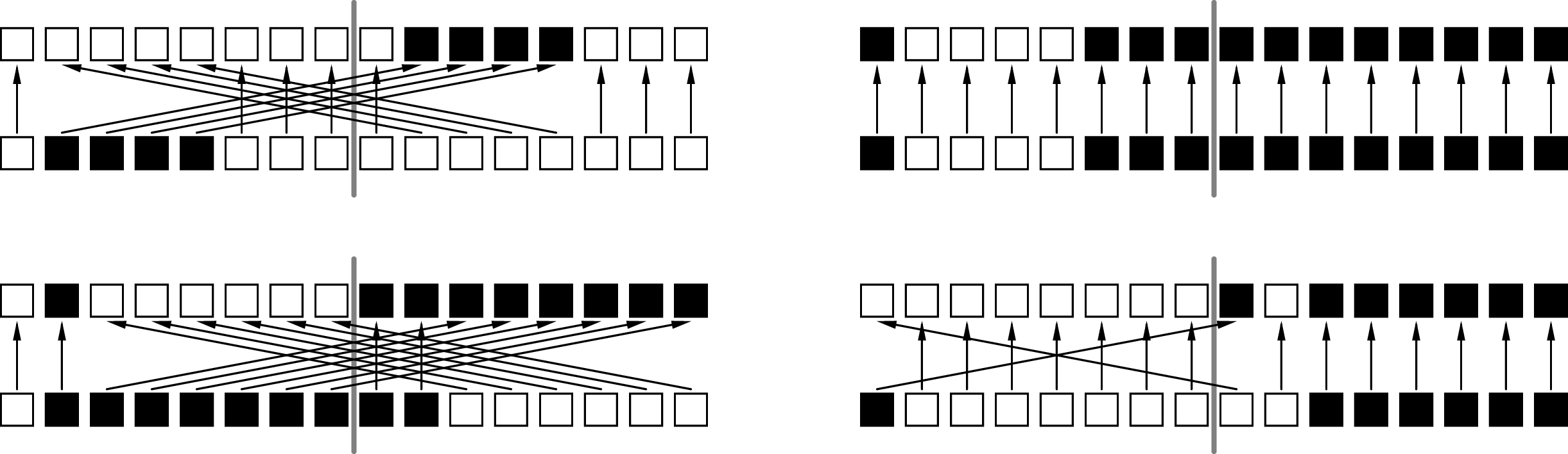
Rys. 2. Cztery przykłady
działania komparatorów na połowach ciągów
bitonicznych.
Białe kwadraty oznaczają 0, a czarne 1.
Z ciągu danego (na dole)
komparatory tworzą ciąg pokazany wyżej
Poszukiwany algorytm sortujący dowolny ciąg długości \(n\) działa na podstawie powyższych spostrzeżeń. Dla ciągu długości \(n=2^m\) składa się on z \(m\) etapów. W \(k\)-tym etapie otrzymywane są posortowane podciągi o długości \(2^k.\) Pierwszy etap, w jednym kroku, porządkuje pary sąsiednich elementów: pierwszy z drugim, trzeci z czwartym itd. W \(k\)-tym etapie pary sąsiednich fragmentów ciągu o długości \(2^{k-1},\) posortowanych niemalejąco, są scalane w jeden fragment, przy czym wcześniej odwracamy kolejność elementów drugiego fragmentu, dzięki czemu uzyskujemy ciąg bitoniczny typu rm. Tak uzyskane ciągi bitoniczne długości \(2^k\) sortowane są w \(k\) krokach przy pomocy opisanej wcześniej procedury. Kolejne wywołania komparatora zilustrowane są na poniższym rysunku (podobnie jak poprzednio, należy go czytać ,,od dołu”).
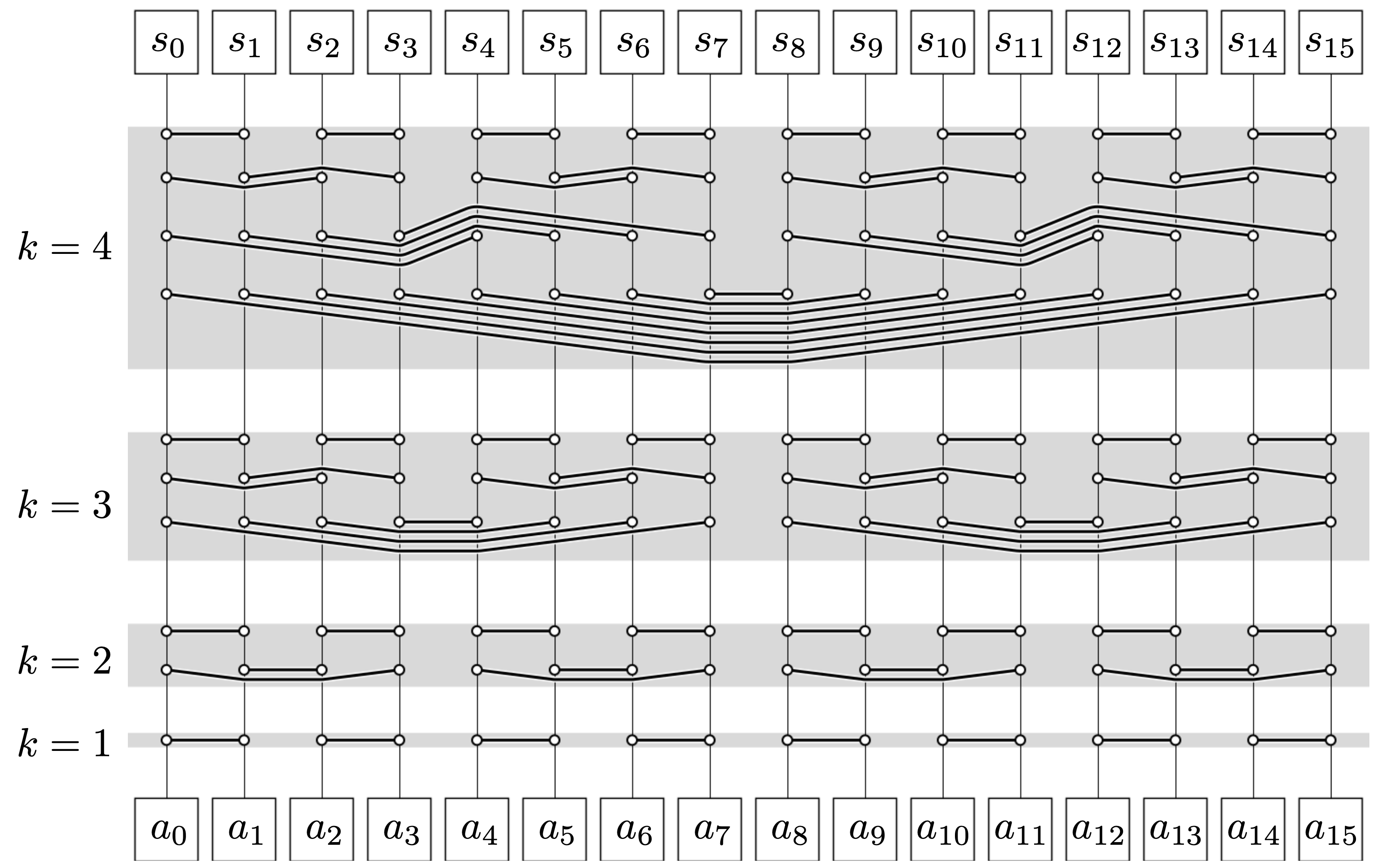
Rys. 3. Sieć sortująca dla ciągów długości \(n=16.\) To, że w ramach każdego etapu pierwsze równoległe wywołania komparatora układają się w ,,koncentryczne łuki”, wynika z opisanego wcześniej odwracania co drugiego z obecnych na danym etapie podciągów celem uzyskania ciągów bitonicznych
Całkowita liczba kroków sortowania w algorytmie wykonującym \(m\) etapów jest równa \(\frac{1}{2}(m^2+m),\) a więc algorytm ten ma rząd złożoności \(\log^2n.\) Jeśli liczba elementów ciągu nie jest potęgą dwójki, to możemy w wyobraźni dopisać na końcu ciągu elementy o wartości \(\infty\) tak, aby otrzymać ciąg o długości \(2^{\lceil \log_2 n \rceil}.\) W implementacji komparator, który miałby sięgnąć poza koniec danego ciągu, natychmiast kończy działanie.
Gdybyśmy mieli \(2^{19}\) procesorów, to do posortowania miliona (a nawet \(2^{20}= 1048576\)) elementów wystarczyłoby \(210\) kroków. Takiego sprzętu większość Czytelników w domu nie ma, ale karta graficzna, która ma tylko \(1024\) procesory, posortuje milion elementów w \(210\cdot512=107520\) krokach, na jakie całe obliczenie zostanie podzielone przez sterownik. Opis (w postaci abstrakcyjnej) i formalny dowód poprawności tego algorytmu można znaleźć w książce [1], a pełna, działająca na karcie graficznej implementacja w języku GLSL (i różne jej zastosowania) jest przedstawiona w książce [2].
Literatura:
[1] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Wprowadzenie do algorytmów, WNT, Warszawa, 2005.
[2] P. Kiciak: OpenGL i GLSL (nie taki krótki kurs), wyd. II, WSA, Warszawa, 2024.