Afiliacja: Studenci, Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Artykuł opisuje wyniki uzyskane przez autorów, pod opieką Oskara Skibskiego.
Krasnoludy żyją w okolicy Zaczarowanej Góry, w której znajduje się jaskinia smoka. Raz do roku smok składa jedno Zaczarowane Jajo, którego skorupa jest wysoce cenioną przez każdego krasnoluda ozdobą. Aby je ukraść, Król zbiera drużynę, która udaje się na misję do jaskini Smoka. Po wielu latach Król, w obliczu nadchodzącej śmierci, postanowił rozdać drogocenne ozdoby swoim najbardziej zasłużonym wojownikom. Jaj nie można jednak dzielić, bo po stłuczeniu tracą swą wartość. W jaki sposób władca powinien rozdzielić jaja między wojowników?
Formalnie nasz problem zdefiniować możemy następująco. Mamy dany ciąg \(k\) wypraw, czyli podzbiorów \(W_1, \dots, W_k\) zbioru krasnoludów \(N = \{1,\dots,n\}.\) Udział krasnoluda \(i\) to \(u_i = \sum_{i \in W_j} 1/|W_j|\) dla \(i \in N.\) Staramy się znaleźć całkowitoliczbowy podział \(k\) jaj z wypraw, \(x_1 + \dots + x_n = k,\) w którym każda liczba \(x_i \in \mathbb{N}\) jest bliska \(u_i,\) na przykład spełnia \(\lfloor u_i \rfloor \leq x_i \leq \lceil u_i \rceil.\)
Król był sprawiedliwym władcą i dlatego najpierw postanowił ocenić zasługi każdego wojownika. Przejrzał swoje zapiski i za każdą wyprawę, w której \(k\) wojowników zdobyło jajo, każdemu jej uczestnikowi dodał \(1/k\) jaja. Po przejrzeniu wszystkich wypraw wiedział już, jaki był udział każdego wojownika w zebranych przez lata jajach. Udziały nie były jednak liczbami całkowitymi, więc aby rozdzielić jaja, Król postanowił skorzystać ze swojego (chwalonego przez poddanych) intelektu.
Dla przykładu, jeżeli zbiory uczestników kolejnych wypraw to \(W_1 = \{A,B,C\},\) \(W_2=\{B,D\},\) \(W_3 = \{A,B\}\) i \(W_4 = \{A,B,C,D\},\) to udziały kolejnych wojowników wynoszą odpowiednio \(u_A = \frac{1}{3}+\frac{1}{2}+\frac{1}{4} \approx 1{,}08,\) \(u_B = \frac{1}{3}+\frac{1}{2}+\frac{1}{2}+\frac{1}{4} \approx 1{,}58,\) \(u_C = \frac{1}{3}+\frac{1}{4} \approx 0{,}58,\) \(u_D = \frac{1}{2}+\frac{1}{4} = 0{,}75.\)
Pierwszy (zły) pomysł Króla.
No dobrze, wiadomo, że wojownik, którego udział jest równy 3,6 jaja, musi dostać ich przynajmniej 3. Odłożę dla każdego wojownika po części całkowitej jego udziału, a jutro zastanowię się, co zrobić z resztą. Już dość się dzisiaj namęczyłem. Zadowolony Król poszedł spać, a następnego dnia pod prysznicem (pod którym zawsze przychodzą do głowy najlepsze pomysły) doznał olśnienia. Wiem! Dam pozostałe jaja tym wojownikom, których ułamkowe części ich udziałów są największe! Oni są teraz najbardziej poszkodowani! W ten sposób sprawiedliwie zaokrąglę udziały i wszyscy wojownicy będą zadowoleni!
Jeżeli nasz problem przypomina Ci, Czytelniku, przydział miejsc w parlamencie, zajrzyj na trzecią stronę artykułu.
Władca ogłosił swoją decyzję podczas uroczystej kolacji. Niestety wojownicy nie byli zachwyceni. Okazało się, że uczestnikami pierwszych trzech wypraw byli dwaj doświadczeni wojownicy, Alojzy i Bonifacy. Należało im się zatem po 1,5 jaja. W kolejnych pięciu wyprawach udział brała natomiast trójka młodych poszukiwaczy przygód: Cecyl, Dorian i Eugeniusz. Należało im się zatem po 1,(6) jaja. W ogólnym rozrachunku, rozdzielając osiem jaj z tych wypraw, Król dał po jednym każdemu z wojowników, a pozostałe trzy rozdał krasnoludom z największą resztą, czyli Cecylowi, Dorianowi i Eugeniuszowi. Alojzy i Bonifacy zaczęli protestować: przecież wspólnie zdobyli trzy jaja, a król dał im łącznie tylko dwa! Król zrozumiał, że jeśli chce uniknąć buntu części swoich wojowników, musi znaleźć lepszy sposób na podział łupu.
Chcemy więc, aby dla każdego \(S \subseteq N\) zachodziło \(\sum_{i \in S} x_i \ge |\{j : W_j \subseteq S\}|.\) O tej własności można myśleć jak o stabilności – żadnej grupie nie opłaca się wyłamać i dzielić się samemu jajami, które zdobyli jej członkowie.
Jeżeli nasz problem przypomina Ci teraz, Czytelniku, definicje rdzenia w grach koalicyjnych, zajrzyj na trzecią stronę artykułu.
Jak uniknąć buntu?
Król myślał intensywnie przez kolejny tydzień, codziennie przez pół godziny. Czy w ogóle da się tak zaokrąglić udziały krasnoludów, aby każda grupa dostała przynajmniej tyle jaj, ile sama przyniosła, czyli tyle, ile było wypraw złożonych tylko z wojowników tej grupy?
Szukając w swoim pomyśle źródła konfliktu, władca zauważył pewną zależność. Jeżeli każdy krasnolud dostanie tylko jaja pochodzące z wypraw, w których brał udział, to nigdy nie nastąpi sytuacja, w której członkowie pewnej grupy dostaną kolektywnie mniej, niż sami wypracowali. Czy jednak da się znaleźć takie dopasowanie jaj do uczestników wypraw, aby każdy dostał swój udział zaokrąglony do liczby całkowitej?
Jestem na to za stary. Niech sami sobie radzą – pomyślał król. Rozłożył wszystkie jaja na stole i przy każdym umieścił tabliczkę z informacją o tym, jacy wojownicy zdobyli to jajo. Następnie zwołał wszystkich krasnoludów i rzekł:
Wojownicy! Bierzcie na zmianę po jednym jaju, przy którym widnieje wasze imię, aż nie uzyskacie części całkowitej swojego udziału! Jeżeli nie będzie wolnego jaja z waszym imieniem, to spróbujcie się wymieniać: poproście pewnego współtowarzysza waszej wyprawy, aby oddał wasze wspólne jajo, a sam wziął wolne ze stołu. Jeżeli takiego nie będzie, to niech poprosi kolejnego o jajo i tak dalej – ktoś wreszcie powinien móc wziąć jajo ze stołu.
Krasnoludy szamotały się trochę, ale już po kwadransie każdy krasnolud miał tyle jaj, ile powinien mieć!
Czy król miał szczęście? Okazuje się, że nie! Powyższa procedura zawsze przydzieli krasnoludom pożądaną liczbę jaj!
Jeżeli nasz problem tym razem przypomina Ci, Czytelniku, szukanie skojarzeń w grafie dwudzielnym, zajrzyj na trzecią stronę artykułu.
Aby to pokazać, załóżmy nie wprost, że jest pewien krasnolud, powiedzmy Eugeniusz, który nie ma jeszcze części całkowitej swojego udziału i nie może już wziąć żadnego jaja ze stołu ani się powymieniać, aby je dostać. Niech \(M\) będzie zbiorem krasnoludów, do którego należy Eugeniusz oraz wszystkie inne krasnoludy, które były z Eugeniuszem na wyprawie, a także te, które były na wyprawie z tymi, z którymi był on na wyprawie, i tak dalej. Niech \(m\) oznacza łączną liczbę jaj posiadanych przez krasnoludy z \(M.\) Ile wynosi \(m\)?
Na pewno mają oni mniej jaj niż wynosi suma ich udziałów, bo wszyscy mają nie więcej niż swoje udziały, a Eugeniusz ma mniej; ich łączny udział w wyprawie \(W_i\) to \(|W_i \cap M|/|W_i|,\) więc \(m < \sum_{W_i \cap M \neq \emptyset} |W_i \cap M|/|W_i|.\)
Z drugiej strony, jeżeli pewien krasnolud miałby jajo, w którego zdobyciu uczestniczył ktoś z \(M,\) to sam też należałby do \(M.\) Wynika z tego, że wszystkie jaja z wypraw krasnoludów z M są w ich posiadaniu: \({m \ge |\{i : W_i \cap M \neq \emptyset\}| = \sum_{W_i \cap M \neq \emptyset} 1}.\)
Obie nierówności prowadzą do sprzeczności, z czego wynika, że na koniec procedury wszyscy muszą mieć już części całkowite swoich udziałów.
Co zrobić z pozostałymi jajami?
Krasnoludy, których udział był całkowity, miały już cały swój udział. Pozostałe jednak wciąż liczyły na dodatkowe jajo. Skoro wcześniejsza metoda okazała się tak skuteczna, ucieszony król postanowił ją kontynuować:
Poddani! Ustawcie się w kolejce zgodnie z tym, ile jeszcze Wam brakuje do całego udziału (czyli w kolejności największych części ułamkowych), i niech każdy spróbuje tak jak poprzednio wziąć jedno dodatkowe jajo.
Gdy krasnoludy ustawiły się zgodnie z tą kolejnością (remisy były rozstrzygane osobistymi preferencjami Króla) i zaczęły brać jaja, i się wymieniać, okazało się, że udało się rozdzielić wszystkie pozostałe jaja pomiędzy wojowników!
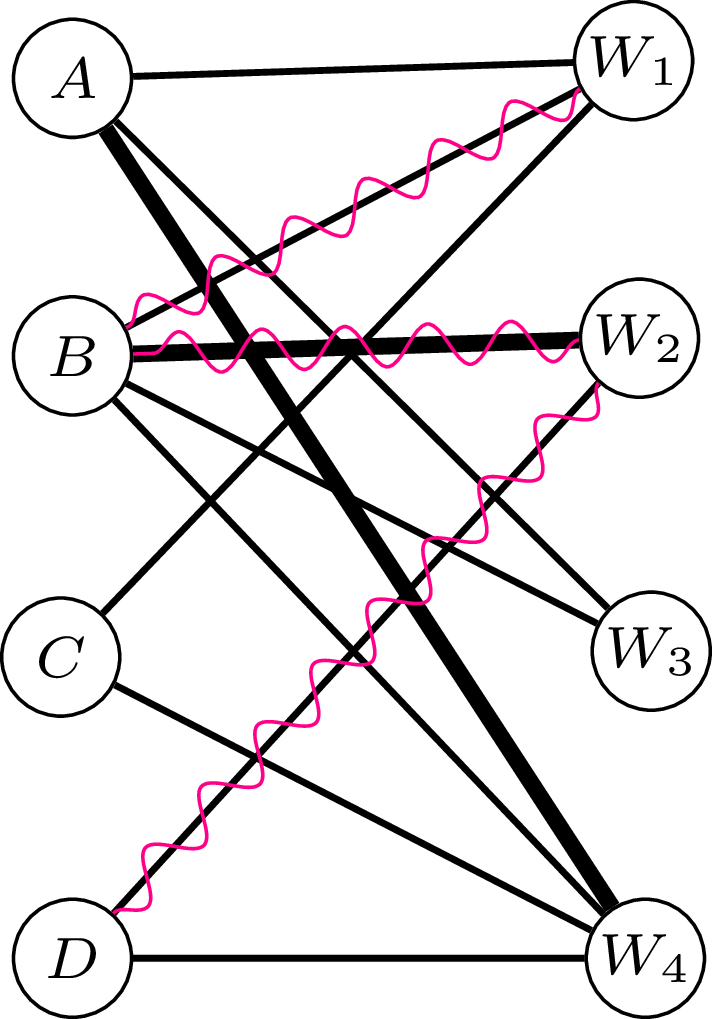
Kontynuując przykład z marginesu, krasnolud \(A\) mógł wziąć jajo z wyprawy \(W_4,\) a \(B\) – jajo z wyprawy \(W_2.\) Potem ustawili się w kolejności \(D,B,C,A.\) Krasnolud \(D\) nie miał na stole już jaja ze swoim imieniem, dlatego musiał się wymienić – wziął jajo z wyprawy \(W_2\) od krasnoluda \(B,\) a ten w zamian wziął jajo z wyprawy \(W_1\) ze stołu. Potem krasnolud \(B\) wziął ze stołu jajo z wyprawy \(W_3\) i procedura zakończyła się podziałem \(4 = 1+2+0+1.\)
Ponownie okazuje się, że taki obrót spraw nie był dziełem przypadku, a powyższa procedura zawsze rozdystrybuuje wszystkie jaja pomiędzy wojowników.
Aby to pokazać, załóżmy nie wprost, że na koniec procedury zostały jaja, których żaden krasnolud, który nie ma jeszcze całego swojego udziału, nie mógł wziąć w swojej kolejce, a więc tym bardziej na koniec procedury. Niech \(K\) będzie zbiorem krasnoludów, które mogą zdobyć pozostałe jaja. Musi zatem być tak, że każdy wojownik w tym zbiorze ma już co najmniej swój pełny udział. Niech \(k\) oznacza to, ile mają już łącznie jaj.
Na pewno mają oni nie mniej jaj niż suma ich udziałów. Ich udział w wyprawie \(W_i\) to \(|W_i \cap K|/|W_i|,\) więc \(k \ge \sum_{W_i \cap K \neq \emptyset} |W_i \cap K|/|W_i|.\)
Z drugiej strony, każde jajo, w zdobyciu którego uczestniczył ktoś spoza \(K,\) musi być wzięte przez krasnoluda spoza \(K.\) W przeciwnym razie ktoś spoza \(K\) mógłby się wymienić z kimś z \(K,\) aby zostało mniej jaj. Zatem krasnoludy z \(K\) posiadają wyłącznie jaja z wypraw, do których należały tylko krasnoludy z \(K.\) Część z tych jaj jest jeszcze niewzięta, gdyż zostały wolne jaja, więc takich jaj jest więcej niż \(k\): \(k < |\{i : W_i \subseteq K \}|.\)
Obie nierówności prowadzą do sprzeczności. Zatem na koniec procedury wszystkie jaja będą rozdane!
Można pokazać, że uzyskany przez Króla podział jest najbliższym (w sensie odległości euklidesowej) stabilnym zaokrągleniem wektora udziałów.
Coś mi to przypomina…
Królowi udało się wymyślić, jak podzielić jaja, ale czy rozwiązania jego problemu nie dało się już znaleźć w przepastnej królewskiej bibliotece?
Jaja to miejsca w parlamencie?
Bardzo podobnym problemem do naszego wydaje się przydział miejsc w parlamencie. W tym problemie daną mamy liczbę miejsc \(k\) oraz liczby głosów \((g_1,\dots,g_n),\) jakie uzyskały kolejne partie. Niech \(G = \sum_i g_i.\) Staramy się rozdzielić \(k\) miejsc w parlamencie między partie w taki sposób, aby procent zdobytych miejsc był bliski procentowi głosów: \(u_i = g_i/G.\)
Metoda wymyślona przez króla pod prysznicem odpowiada metodzie największych reszt: przydzielamy wszystkim partiom po \(\lfloor u_i \rfloor\) miejsc, a potem po jednym dodatkowym miejscu przyznajemy tym z nich, dla których \(u_i - \lfloor u_i \rfloor\) jest największe. Metoda D’Hondta, stosowana w Polsce, także dałaby niestabilny podział, a na dodatek mogłaby dać komuś więcej niż \(\lceil u_i \rceil\) (np. ktoś z udziałem \(2{,}5\) mógłby dostać \(4\) jaja). Nawet gdyby król znał te metody, za bardzo by mu one nie pomogły – wykorzystują tylko liczby \(u_i,\) więc nie mogą być stabilne.
O problemie podziału miejsc w parlamencie pisaliśmy w Delcie \(\Delta^{11}_{12}\).
Jaja to wypłata w grze koalicyjnej?
Bardziej adekwatnym modelem wydają się gry koalicyjne. Gra koalicyjna to para \((N,v),\) gdzie \(N\) to zbiór graczy i \(v: 2^N \rightarrow \mathbb{R}\) to funkcja przypisująca każdej koalicji (czyli po prostu grupie) graczy pewną wartość, przy czym \(v(\emptyset) = 0.\) Podstawowym problemem jest podział wartości \(v(N)\) pomiędzy graczy: \(\sum_{i \in N} x_i = v(N).\) Mówi się, że podział jest w rdzeniu, jeżeli wypłata każdej koalicji jest co najmniej równa jej wartości: \(\sum_{i \in S} x_i \ge v(S).\) Najsłynniejszym sposobem podziału jest wartość Shapleya.
O grach koalicyjnych pisaliśmy między innymi w Delcie \(\Delta^{11}_{20}\) oraz \(\Delta^{4}_{22}\).
Jeżeli potraktujemy krasnoludów jako graczy, to za wartość koalicji \(v(S)\) możemy przyjąć liczbę jaj zdobytych przez nich bez pomocy innych: \(v(S) = |\{ j : W_j \subseteq S\}|.\) Łatwo sprawdzić, że przy takiej definicji udział to właśnie wartość Shapleya, a nasza stabilność jest równoważna byciu w rdzeniu. Dla różnych zbiorów jaj możemy dostać wszystkie całkowitoliczbowe gry pozytywne. Wiadomo, że wartość Shapleya takich gier jest w rdzeniu, ale czy pewne jej zaokrąglenie też jest? Do dnia dzisiejszego świat tego nie wiedział, ale nasz artykuł pokazuje, że tak! Można nawet pokazać, że jest to prawdą dla wszystkich gier wypukłych!
Gry pozytywne to gry, w których dywidendy wszystkich koalicji są nieujemne. Dywidenda koalicji \(S\) w grze \((N,v)\) jest nadwyżką koalicji \(S,\) czyli wartością koalicji pomniejszoną o nadwyżki podkoalicji: definiuje się ją jako \(\Delta_v(S) = v(S) - \sum_{T \subsetneq S} \Delta_v(T)\) przy założeniu \(\Delta_v(\emptyset)=0.\)
Graf dwudzielny reprezentujący przykład z marginesu: 4 krasnoludy i 4 jaja z ich wypraw. Linie pogrubione to skojarzenie uzyskane po przydzieleniu pierwszych jaj. Zawijane kolorowe linie odpowiadają ścieżce powiększającej, czyli wymianie, dzięki której \(D\) dostaje jajo.
Jaja to wierzchołki w grafie?
Najbardziej przydatne okazuje się spojrzenie na nasz problem jako na graf dwudzielny: krasnoludy będą wierzchołkami po lewej, a jaja – po prawej stronie. Krawędziami łączymy teraz każde jajo z krasnoludami, którzy uczestniczyli w jego zdobyciu. Użyjemy pojęcia skojarzenia – jest to podzbiór krawędzi, w których każdy wierzchołek jest końcem nie więcej niż jednej krawędzi; wierzchołki, które są końcami, nazywamy skojarzonymi. Powielmy wierzchołek każdego krasnoluda \(\lceil u_i \rceil\) razy. Teraz nasz problem sprowadza się do znalezienia skojarzenia, w którym wszystkie wierzchołki z prawej strony są skojarzone i użyliśmy nie mniej niż \(\lfloor u_i \rfloor\) wierzchołków każdego krasnoluda. Tylko jak to zrobić? I czy tak się w ogóle da?
Podążając za mądrością króla, najpierw przydzielmy części całkowite. Zakryjmy po jednym wierzchołku każdego krasnoluda i znajdźmy skojarzenie, w którym to wszystkie wierzchołki z lewej są skojarzone. Korzystając z Twierdzenia Halla, możemy wykazać (podobnie jak w naszym dowodzie), że zawsze jest to możliwe. Następnie po kolei odkrywamy po jednym wierzchołku i, jeżeli się da, powiększamy skojarzenie. Znowu można wykazać, że w ten sposób skojarzymy wszystkie jaja.
Twierdzenie Halla (patrz \(\Delta^{10}_{24}\)): Niech \(A_i\) będzie zbiorem wierzchołków połączonych z wierzchołkiem \(i.\) Pełne skojarzenie lewej strony w prawą istnieje wtedy i tylko wtedy, gdy dla każdego podzbioru wierzchołków \(S\) z lewej strony zachodzi \[|S| \le \Bigl|\bigcup_{i~\in S} A_i\Bigr|.\]
A jak te skojarzenia znaleźć? Załóżmy, że po pewnej liczbie kroków mamy już pewne skojarzenie, czyli przyporządkowanie jaj. Aby je powiększyć, możemy znaleźć ścieżkę powiększającą, czyli ścieżkę, która zaczyna się i kończy na wierzchołku nieskojarzonym i w której na zmianę mamy krawędź ze skojarzenia i nie (przykład można zobaczyć na marginesie). Zamienienie krawędzi ze skojarzenia na pozostałe ze ścieżki powiększa skojarzenie o jedną krawędź. Twierdzenie Berge’a mówi, że skojarzenie jest maksymalne wtedy i tylko wtedy, gdy nie istnieje względem niego żadna ścieżka powiększająca, więc jeżeli skojarzenie nie jest jeszcze maksymalne, to na pewno nam się uda znaleźć taką ścieżkę. A czym są ścieżki powiększające w naszej procedurze? No tak, to system zamian wymyślony przez króla. Trzeba przyznać, że nieźle to król wymyślił…