Klub 44

Termin nadsyłania rozwiązań: 28 II 2025

Zadania z fizyki nr 788, 789

Redaguje Elżbieta ZAWISTOWSKA

788. Na gładkim stole leży układ klocków przedstawiony na rysunku 1. Współczynnik tarcia między klockami o masach $M$ i $m$ wynosi $\mu .$ Klocki o masach $m$ połączone są nieważką, nierozciągliwą nicią. Prawy dolny klocek ciągnięty jest równolegle do stołu siłą $F.$ Znaleźć przyspieszenia wszystkich klocków.

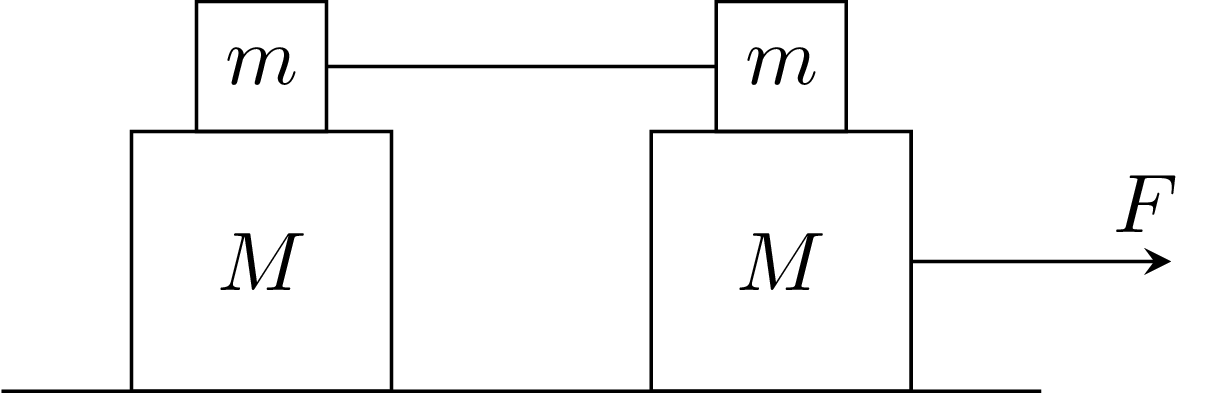    Rys. 1

789. Sześciokątny ołówek popchnięto wzdłuż płaszczyzny poziomej jak na rysunku 2. Jaki musi być współczynnik tarcia $\mu$ między ołówkiem a płaszczyzną, aby ołówek ślizgał się po płaszczyźnie i nie obracał?

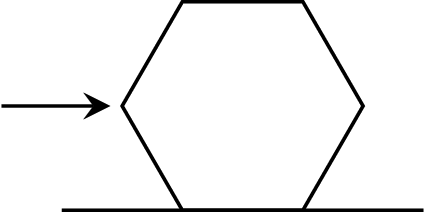Rys. 2

Zadania z matematyki nr 891, 892

Redaguje Marcin E. KUCZMA

891. Znaleźć wszystkie liczby rzeczywiste $\phi ,$ spełniające dla każdej liczby całkowitej $n\ge 0$ warunek: $\cos (2^n\phi )\le 0.$

892. Dana jest liczba naturalna $n\ge 2.$ W turnieju badmintona bierze udział $n$ zawodników; każdy z każdym rozgrywa jeden mecz, nie ma remisów. Dla każdej liczby $k\in \{0,\dots ,n-1\}$ wyznaczyć maksymalną wartość, jaką może osiągnąć liczba zawodników, którzy zakończyli turniej, mając dokładnie $k$ wygranych meczów.

Zadanie 892 zaproponował pan Michał Adamaszek z Kopenhagi.