Papierem na księżyc

Afiliacja: Student, Wydział Fizyki, Uniwersytet Warszawski

Znanym faktem jest, że zginając kartkę wpół, dokonujemy jej dwukrotnego pogrubienia. Z każdym zgięciem następne jest coraz trudniejsze – aż do momentu, w którym dokonanie jeszcze jednego jest już niemożliwe. Nasuwa się więc nieuchronne pytanie: ile właściwie razy można zgiąć daną kartkę wpół? Tę właśnie liczbę spróbujemy wyznaczyć, przyjmując, że kartkę zginać będziemy naprzemiennie po długości i szerokości. Niech \(n\) oznacza liczbę dokonanych zgięć; \(\mathcal{L}_n,\) \(\mathcal{W}_n,\) \(\mathcal{D}_n\) – odpowiednio: długość, szerokość i grubość kartki po \(n\) zgięciach. Na początek zdefiniujmy założenia, na których będziemy bazować podczas dalszego zgłębiania pomysłu:

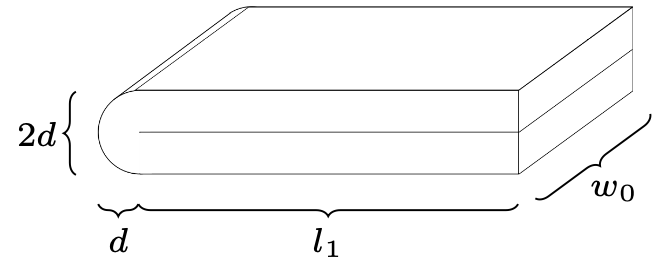
Rys. 1. Pierwsze zagięcie – wykonane równolegle do krawędzi szerokości

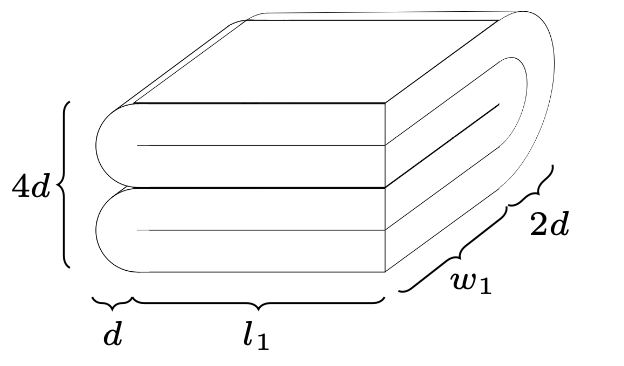
Rys. 2. Drugie zagięcie – wykonane równolegle do krawędzi długości

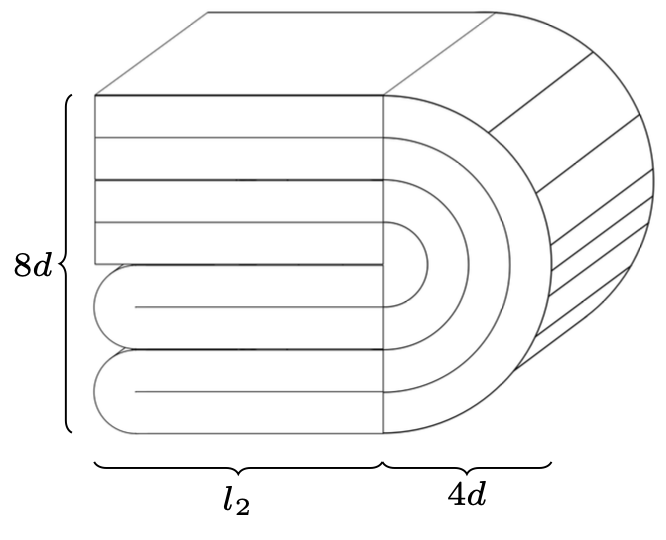
Rys. 3. Trzecie zagięcie – wykonane równolegle do krawędzi szerokości

1. Złożenie kartki wpół oznacza, że na ,,zewnątrz” zagięcia powstaje łuk kolisty o takiej długości, by suma ,,zewnętrznej” powierzchni odpowiadała powierzchni kartki przed złożeniem.

2. ,,Wewnętrzna” część zagięcia jest punktowa – kartka zostaje w tym miejscu ,,złamana”.

3. Konsekwencją punktów 2 i 3 jest fakt, że objętość kartki na obszarze zagięcia maleje dwukrotnie. Przyjąć więc można jedną z dwóch możliwych interpretacji:

   • średnia gęstość kartki na zagięciu jest dwukrotnie większa niż przed wykonaniem zgięcia,

   • po wykonaniu zagięcia po stronie przeciwnej niż nowo utworzony łuk powstaje klin ,,kompensujący” ubytek w objętości.

   Niezależnie od tego, którą z powyższych opcji przyjmiemy, warunki 1 i 2 pozostają spełnione.

Tym samym możemy rozpocząć naszą przygodę .

W celu ułatwienia obliczeń wprowadźmy oznaczenia (jak na rysunkach): \(l_m\) – długość płaszczyzny kartki (bez łuku), \(w_u\) – adekwatnie, szerokość płaszczyzny, \(d\) – początkowa grubość kartki, gdzie \(m\) oraz \(u\) należą do zbioru \(\{0,1,2,\dots\}.\)
W pierwszej kolejności wyraźmy grubość kartki po \(n\) zgięciach: \[\begin{gathered} \mathcal{D}_n = d\cdot 2^{n}. \end{gathered}\] Dalej przyjmijmy następującą definicję długości i szerokości: operację rozpoczynamy od wykonania zagięcia równoległego do krawędzi szerokości \(\mathcal{W},\) następnie do krawędzi długości \(\mathcal{L},\) znowu \(\mathcal{W}\) itd. Długość i szerokość wybieramy więc, określając kolejność wykonywanych zgięć (\(l_0\) sprzecznie z lingwistyczną konwencją nie musi być większe od \(w_0\)).

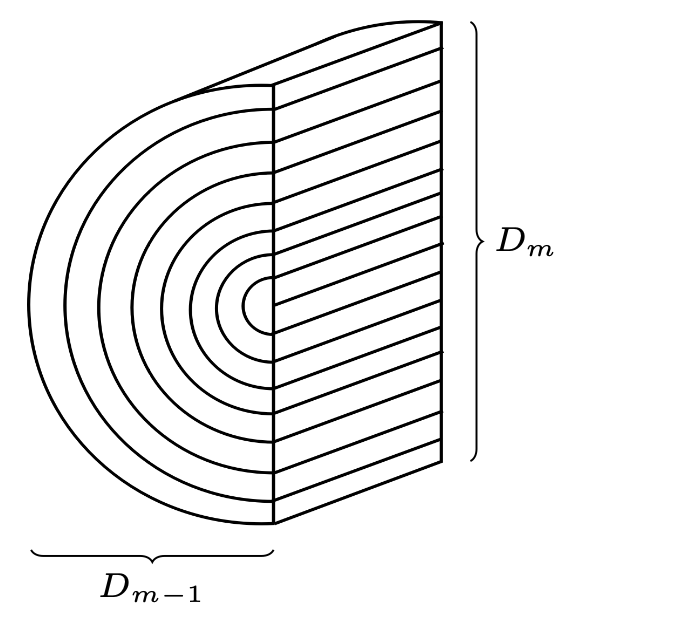
Mając tę postać, można już utworzyć wzór ogólny na \(l_m\) (oczywiście dla \(m > 0)\!:\) \[\begin{gathered} l_m = \frac{1}{2}(l_{m-1}+ \lfloor 4^{m-2}\rfloor d - \pi \cdot 4^{m-1} d). \end{gathered}\] Rozwijając powyższą rekurencję (podstawiamy kolejno wzory pod \(l_{m-1},\) potem \(l_{m-2}\) itd.), dostajemy sumę, którą można na powrót zwinąć, stosując wzór na sumę ciągu geometrycznego, i zastępujemy tym samym wzór rekurencyjny iteracyjnym: \[\begin{gathered} l_m = \frac{1}{2^{m}}l_0 + d\left[\frac{1}{2^{m-1}}\frac{1-8^{m-1}}{1-8}\right] - \pi d{\left[\frac{1}{2^{m}}\frac{1-8^{m}}{1-8}\right]}. \end{gathered}\] Wyobraźmy sobie teraz przypadek skrajny, po którego przekroczeniu wykonanie następnego zgięcia będzie niemożliwe (rys. 4).

Rys. 4. Skrajny przypadek (kartki nie da się już złożyć)

Widać, że zachodzić musi: \[\begin{gathered} l_m \geq 0. \end{gathered}\] Z tego warunku, po krótkich przekształceniach, otrzymujemy nierówność: \[\begin{gathered} m \leq \log_8\left(\frac{\frac{7}{d}l_0 - 2 + \pi}{\pi - \frac{1}{4}}\right). \end{gathered}\] Podobne wyprowadzenie przeprowadzamy dla szerokości \(w_u\) i otrzymujemy: \[\begin{gathered} u~\leq \log_8\left(\frac{\frac{7}{2d}w_0 - 2 + \pi}{8\pi - 2}\right) + 1. \end{gathered}\] Wystarczy teraz określić liczbę zgięć wzdłuż krawędzi \(\mathcal{L}\) i \(\mathcal{W}.\) Ponieważ liczba zgięć jest liczbą całkowitą oraz zachodzą nierówności postaci \(m,u\leq\dots,\) mamy: \[\begin{gathered} m = {\left\lfloor\log_8\left(\frac{\frac{7}{d}l_0 - 2 + \pi}{\pi - \frac{1}{4}}\right)\right\rfloor},\\ u ={ \left\lfloor\log_8\left(\frac{\frac{7}{2d}w_0 - 2 + \pi}{\pi - \frac{1}{4}}\right)\right\rfloor}. \end{gathered}\] Powyższe równości określają maksymalną liczbę zgięć kolejno dla krawędzi \(\mathcal{L}\) i \(\mathcal{W}\) (przy założeniu, że przy zginaniu jednej z krawędzi było możliwe zgięcie tej drugiej).

Jeśli \(m>u,\) mamy ciąg zgięć (np. tutaj \(m=n+3\)): \[\begin{gathered} \underbrace{\begin{array}{@{}c@{}}^1\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^1\\[-2pt]\mathcal{W} \end{array} \rightarrow \begin{array}{@{}c@{}}^2\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^2\\[-2pt]\mathcal{W} \end{array} \rightarrow \dots \rightarrow \begin{array}{@{}c@{}}^u\\[-2pt]\mathcal{W} \end{array} \rightarrow \begin{array}{@{}c@{}}^{m-2}\\[-2pt]\mathcal{L} \end{array}}_{\mbox{Cały możliwy do wykonania ciąg zgięć}} \rightarrow \begin{array}{@{}c@{}}^{m-1}\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^m\\[-2pt]\mathcal{L} \end{array}. \end{gathered}\] Czyli całkowita liczba zgięć dla \(m>u\) to \(n = 2u + 1.\)
Jeśli natomiast \(m\leq u,\) mamy ciąg zgięć (np. tutaj \(m=u-3\)): \[\begin{gathered} \underbrace{\begin{array}{@{}c@{}}^1\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^1\\[-2pt]\mathcal{W} \end{array} \rightarrow \begin{array}{@{}c@{}}^2\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^2\\[-2pt]\mathcal{W} \end{array} \rightarrow \dots \rightarrow \begin{array}{@{}c@{}}^m\\[-2pt]\mathcal{L} \end{array} \rightarrow \begin{array}{@{}c@{}}^{u-2}\\[-2pt]\mathcal{W} \end{array}}_{\mbox{Cały możliwy do wykonania ciąg zgięć}} \rightarrow \begin{array}{@{}c@{}}^{u-1}\\[-2pt]\mathcal{W} \end{array} \rightarrow \begin{array}{@{}c@{}}^u\\[-2pt]\mathcal{W} \end{array}. \end{gathered}\] Czyli całkowita liczba zgięć dla \(m\leq u\) to \(u = 2m.\) Ogólny wzór na \(n\) ma postać:

Przetestujmy teraz nasz algorytm.

Biurowa kartka papieru w formacie A4 ma standardowo wymiary: \(297 \times 210 \times 0{,}1\) mm. Podstawiając je odpowiednio do ustalonych wzorów, sprawdzimy, ile razy można zgiąć kartkę wzdłuż długości i szerokości (pamiętając jednocześnie, że długość w naszym problemie to krawędź, w poprzek której wykonujemy pierwsze zagięcie). \[\begin{aligned} \mbox{dla }l_0=297&\text{~mm}\mbox{ i }w_0=210\text{~mm}\\ m &= \left\lfloor4{,}27\right\rfloor = 4\\ u &= \left\lfloor3{,}77\right\rfloor = 3\\ m>u&\Rightarrow \boxed{n = 2u + 1 = 7} \end{aligned}\] \[\begin{aligned} \mbox{dla }l_0=210&\text{~mm}\mbox{ i }w_0=297\text{~mm}\\ m &= \left\lfloor4.103\right\rfloor = 4\\ u &= \left\lfloor3.937\right\rfloor = 3\\ m>u&\Rightarrow \boxed{n = 2u + 1 = 7} \end{aligned}\]

Widać, że kartkę papieru w formacie A4 można zgiąć co najwyżej 7 razy, co zgadza się z popularną miejską legendą.

Po przeprowadzeniu podobnych obliczeń dla kartki A3 o tej samej grubości (\(297\times 420\times 0{,}1\) mm) okazało się, że bardziej opłacalnym jest przyjąć \(l_0=297\) mm i \(w_0=420\) mm (krótsza krawędź jest zginana jako pierwsza), co daje nam maksymalną liczbę zgięć równą 8.

Papierem na Księżyc.

Dochodzimy do miejsca, w którym spełnimy obietnicę z tytułu. Spróbujmy ustalić wymiary kartki papieru o grubości \(d=0{,}1\) mm potrzebnej do zbudowania połączenia między powierzchniami Ziemi i Księżyca wyłącznie przez wielokrotne zginanie jej wpół. Średnia odległość między powierzchniami Ziemi i Księżyca wynosi około \(376\,291\) km. Policzmy, ile razy należałoby złożyć naszą kartkę papieru, aby dosięgnąć do Księżyca. \[\begin{aligned} D_n &= S_{zk} = 376\,291\text{~km} = 376\,291\cdot10^{6}\text{~mm} = 0{,}1\text{~mm}\cdot2^n,\\ n &= \left\lceil\log_2\left(\frac{376\,291\cdot10^{6}\text{~mm}}{0{,}1\text{~mm}}\right)\right\rceil = \left\lceil41{,}775\right\rceil = 42. \end{aligned}\] \(n=42\) jest liczbą parzystą, więc mamy przypadek \(n=2m,\) czyli nastąpi taka sama liczba zgięć wzdłuż długości i szerokości \(m=u=21.\) Kontynuujemy obliczenia, przywołując wzory na \(m\) i \(u,\) i otrzymujemy wymiary (\(l_0\times w_0\)): \[\begin{gathered} \textcolor{var(--primary-color)}{2546{,}85 \text{ au}\times5093{,}7 \text{ au}} \end{gathered}\] (\(1\) au \(\approx 150\cdot 10^6\) km).

Układ Słoneczny.

Chcąc wyobrazić sobie rozmiar naszej kartki, możemy porównać ją z rozmiarami Układu Słonecznego, którego promień szacowany jest na około \(R_s = {4\,498\,252\,900}\) km (średnia odległość Neptuna od Słońca).
Porównajmy pole powierzchni kartki \(P_k\) z powierzchnią Układu Słonecznego \(P_s\) (a raczej polem powierzchni koła o krawędzi zarysowanej przez uśrednioną orbitę Neptuna): \[\begin{aligned} &P_k = l_0\cdot w_0 = 2{,}903271\cdot10^{23}\text{~km}^2,\\ &P_s = \pi R_s^2 = 6{,}356786\cdot10^{19}\text{~km}^2,\\ &\frac{P_k}{P_s} = 4567{,}1995. \end{aligned}\] Przez fakt posiadania bez mała \(4600\)-krotności powierzchni aktualnie zamieszkiwanego przez nas układu planetarnego oczywistym jest, że nasza kartka bez wątpienia zasługuje na miano megastruktury.

Dla zobrazowania skali wielkości naszej kartki możemy porównać ją z najodleglejszym od Ziemi obiektem wysłanym przez człowieka – sondą misji Voyager I (korzystając z danych na moment: 00:00 UTC 01.01.2025): \[\begin{aligned} V_{v_I}& = 16{,}9995\ \frac{\mbox{km}}{\mbox{s}},\ \ \ R_{v_I} = 24~798~697~389\text{~km},\ \ \ t = \frac{\sqrt{\frac{P_k}{\pi}}-R_{v_I}}{V_{v_I}}. \end{aligned}\] Zakładając, że sonda będzie leciała ze stałą prędkością \(V_{v_I}\) – osiągnie punkt, w którym pole powierzchni \(P_{v_I} = \pi R_{v_I}^2\) stycznego do niego koła (ze środkiem w Słońcu) będzie identyczne z polem naszej kartki papieru, w \(\textcolor{var(--primary-color)}{2545}\) roku.

Alternatywy.

Ostatecznie wartym nadmienienia jest fakt, iż powyższe ustalenia poprawne są wyłącznie dla składania naprzemiennego (wzdłuż krawędzi \(\mathcal{L}\) i \(\mathcal{W}\)).

Analogiczną metodą Czytelnik może wyprowadzić wzór dla kolejnych złożeń równolegle do wyłącznie jednej, wybranej krawędzi kartki papieru. Tym sposobem ustalić można, na przykład, przewidywaną liczbę złożeń całej rolki papieru toaletowego.