Zadania

Dane są dwa ciągi arytmetyczne, $a_1,$ $a_2,$ $\dots$ i $b_1,$ $b_2,$ $\dots ,$ składające się z liczb całkowitych dodatnich. Wiadomo, że $a_1=b_1$ oraz dla każdej liczby całkowitej $n\ge 1$ liczby $a_n$ i $b_n$ dają równe reszty z dzielenia przez $n.$ Udowodnić, że te ciągi są identyczne.

Dane są dwa ciągi liczb całkowitych dodatnich $x_1,$ $x_2,$ $\dots ,$ $x_m$ oraz $y_1,$ $y_2,$ $\dots ,$ $y_n,$ których sumy $x_1+x_2+\dots +x_m$ i $y_1+y_2+\dots +y_n$ są równe $s<nm.$ Udowodnić, że w równości $$x_1+x_2+\dots +x_m=y_1+y_2+\dots +y_n$$ można wykreślić część składników, zachowując jej prawdziwość.

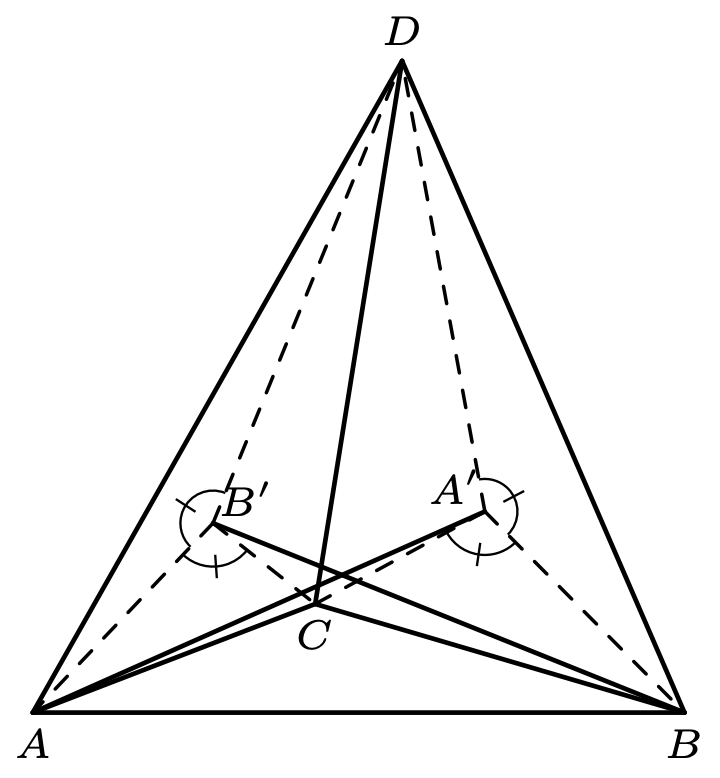
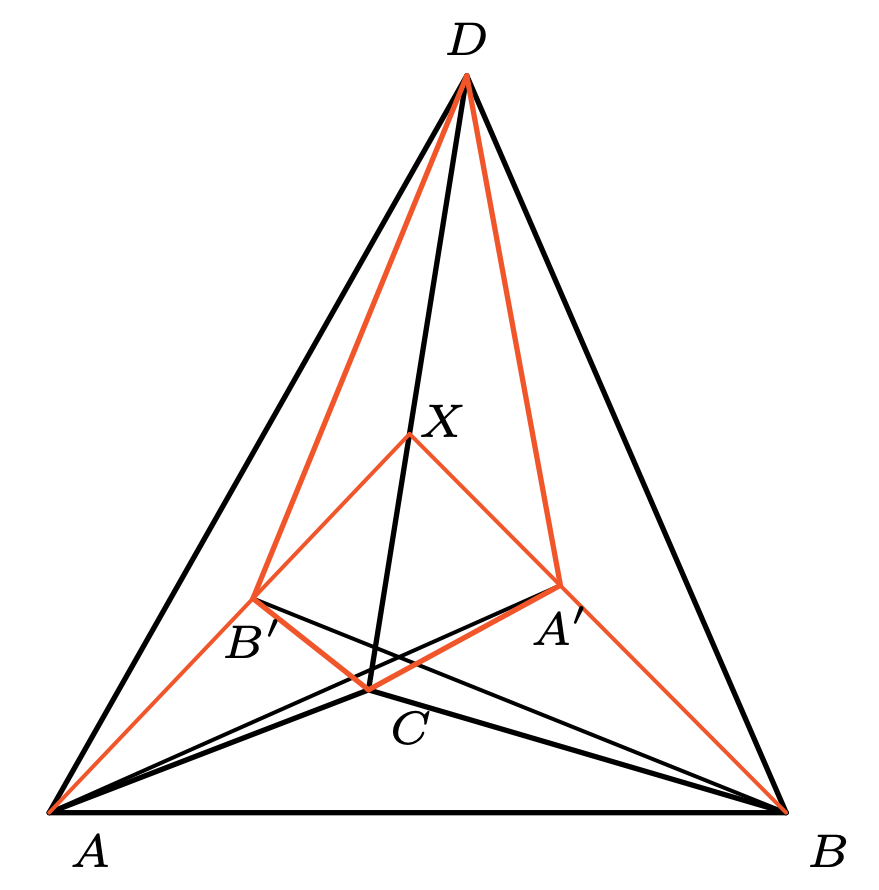
W czworościanie $ABCD$ na ścianach $BCD$ i $ACD$ znajdują się, odpowiednio, punkty $A^{\prime }$ oraz $B^{\prime }$ takie, że $$\measuredangle A{B}^{\prime }C=\measuredangle A{B}^{\prime }D=\measuredangle B{A}^{\prime }C=\measuredangle B{A}^{\prime }D={120}^{\circ }.$$ Wiadomo, że proste $A{A}^{\prime }$ i $B{B}^{\prime }$ przecinają się. Udowodnić, że odległości punktów $A^{\prime }$ oraz $B^{\prime }$ od prostej $CD$ są równe.

Planeta o masie $m$ obiega Słońce po orbicie eliptycznej. W aphelium jej odległość od Słońca wynosi $A,$ a w perihelium $a.$ Ile wynosi moment pędu, $L,$ tej planety? Masa Słońca równa jest $M,$ a stała grawitacji $G.$

W opisanym dalej układzie stojąca fala dźwiękowa może spełniać rolę siatki dyfrakcyjnej dla światła. Kuweta o przezroczystych, płaskich, równoległych ściankach jest wypełniona cieczą. Równolegle do ścianek kuwety w cieczy wzbudzona jest stojąca fala ultradźwiękowa o długości $\mathrm{\Lambda }.$ Wiązka światła laserowego o długości fali $\lambda$ pada prostopadle do ścianek kuwety i do wektora falowego ultradźwięku. Jaki warunek spełniają powstające za kuwetą prążki interferencyjne światła?