Delta 3/2025

Klub 44

Marcin E. Kuczma i Elżbieta Zawistowska

Zadania z matematyki nr 897, 898

Redaguje Marcin E. KUCZMA

897. Czworokąt wypukły $A B C D$ ma obwód długości $p$ oraz przekątne długości $m$ i $n .$ Punkt $E$ jest czwartym wierzchołkiem równoległoboku $A B C E .$ Udowodnić, że $D E \leq p - m - n .$

898. Wyznaczyć wszystkie pary liczb naturalnych $m, n \geq 1,$ dla których wielomian $W (x) = x^{m} + x^{n} + 1$ jest podzielny przez trójmian $T (x) = x^{2} + x + 1 .$

Zadanie 898 zaproponował pan Witold Bednarek z Łodzi.

Rozwiązania zadań z numeru 11/2024

Przypominamy treść zadań:

889. Ciąg $(a_{1}, \dots, a_{N}),$ długości $N,$ ma wyrazy $a_{k} \in {2, 3, 5},$ z sumą $a_{1} + \dots + a_{N} = A .$ Niech $b_{k} = a_{k} a_{k + 1} a_{k + 2} a_{k + 3}$ (gdzie, cyklicznie, $a_{N + i} = a_{i}$ ). Zakładamy, że każda z liczb $b_{1}, \dots, b_{N}$ dzieli się przez $30.$ Przyjmując jako znane wartości $N,$ $A$ (dla których istnieje co najmniej jeden ciąg $(a_{k})$ o podanych własnościach) wyznaczyć wszystkie możliwe wartości sumy $B = b_{1} + \dots + b_{N} .$

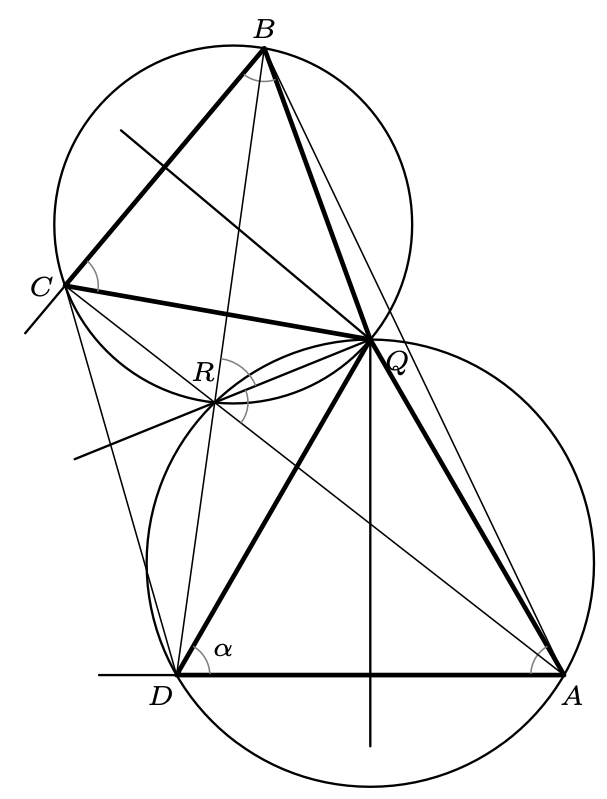
890. W czworokącie wypukłym $A B C D$ przekątne przecinają się w punkcie $P$ ; boki $B C$ i $D A$ nie są równoległe, a ich symetralne przecinają się w punkcie $Q$ (różnym od $P$ ), leżącym wewnątrz czworokąta. Trójkąty $B Q C$ i $D Q A$ są podobne. Udowodnić, że prosta $P Q$ zawiera dwusieczne kątów $A P B$ i $C P D .$

889. Podzielność $30 ∣ b_{k}$ oznacza, że w każdej czwórce kolejnych wyrazów $a_{k}, a_{k + 1}, a_{k + 2}, a_{k + 3}$ są obecne liczby $2, 3, 5$ oraz – powtórnie – jeszcze jedna z nich; nazwijmy ją $c_{k} .$ Wówczas $b_{k} = 30 c_{k},$ zaś $a_{k} + a_{k + 1} + a_{k + 2} + a_{k + 3} = 10 + c_{k} .$ Stąd $\begin{aligned} B & = \sum_{k = 1}^{N} b_{k} = 30 \sum_{k = 1}^{N} c_{k} = 30 \sum_{k = 1}^{N} (a_{k} + a_{k + 1} + a_{k + 2} + a_{k + 3} - 10) = 30 (4 A - 10 N) . \end{aligned}$ Jest to jedyna możliwa wartość sumy $B .$

890. Z określenia $Q$ wynika, że trójkąty podobne $B Q C$ i $D Q A$ są równoramienne: $Q B = Q C,$ $Q D = Q A .$ Oznaczmy $∡ Q B C = ∡ Q C B = ∡ Q A D = ∡ Q D A = α .$ Niech $R$ będzie drugim (poza $Q$ ) punktem przecięcia okręgów opisanych na tych trójkątach. Przyjmijmy (b.s.o.), że proste $B C$ i $D A$ przecinają się w punkcie leżącym na półprostych $B C^{\to}$ i $A D^{\to}$ ; wówczas punkt $R$ leży w obszarze kąta wypukłego $C Q D$ (nie jest możliwe, by punkt $C$ lub $D$ leżał na ,,krótkim” łuku $Q R$ jednego z rozważanych okręgów, bo to by się kłóciło z wypukłością czworokąta $A B C D$ ). Mamy więc konfigurację, jak na rysunku.

W okręgach $B Q C$ i $D Q A$ widzimy kąty wpisane: $\begin{matrix} ∡ B R Q = ∡ B C Q = α, ∡ C R Q = π - ∡ C B Q = π - α, \\ ∡ A R Q = ∡ A D Q = α, ∡ D R Q = π - ∡ D A Q = π - α . \end{matrix}$ Z pierwszej i czwartej równości wynika, że punkt $R$ leży na odcinku $B D$ ; zaś z drugiej i trzeciej – że $R$ leży na odcinku $A C .$ To znaczy, że $R$ jest punktem $P$ z treści zadania. Równości pierwsza z trzecią pokazują, że prosta $Q R$ połowi kąt $A R B$ ; zaś druga z czwartą – że ta prosta połowi kąt $C R D .$ Zważywszy, że $R = P,$ mamy to, co należało udowodnić.

Inna metoda (szkic): stosujemy inwersję o środku $Q$ (i dowolnie ustalonym promieniu dodatnim). Półproste $Q A^{\to},$ $Q B^{\to},$ $Q C^{\to},$ $Q D^{\to},$ $Q P^{\to}$ przechodzą każda na siebie. Obrazami punktów $A, B, C, D, P$ są punkty, które oznaczymy $A^{*}, B^{*}, C^{*}, D^{*}, P^{*},$ leżące odpowiednio na tych półprostych. W mocy pozostają równości $Q B^{*} = Q C^{*},$ $Q D^{*} = Q A^{*} .$ Obrazem prostej $A C$ jest okrąg $Q A^{*} C^{*},$ zaś prostej $B D$ – okrąg $Q B^{*} D^{*}$ (każdy z nich z usuniętym punktem $Q$ ). Punkt $P^{*}$ leży na obu okręgach.

Mamy udowodnić, że prosta $Q P$ tworzy równe kąty z prostymi $A C$ i $B D .$ Inwersja zachowuje równość kątów, więc wystarczy wykazać, że prosta $Q P^{*}$ tworzy równe kąty z okręgami $Q A^{*} C^{*}$ i $Q D^{*} B^{*} .$ Ponieważ $∡ B^{*} Q C^{*} = ∡ D^{*} Q A^{*} = : φ,$ obrót o kąt $φ$ wokół $Q$ przenosi trójkąt $Q A^{*} C^{*}$ na trójkąt $Q D^{*} B^{*} .$ Zatem te trójkąty są przystające – okręgi na nich opisane też są przystające – są więc symetryczne względem wspólnej cięciwy $Q P^{*} .$ Stąd wymagana równość kątów i teza zadania.

Zadania z fizyki nr 794, 795

Redaguje Elżbieta ZAWISTOWSKA

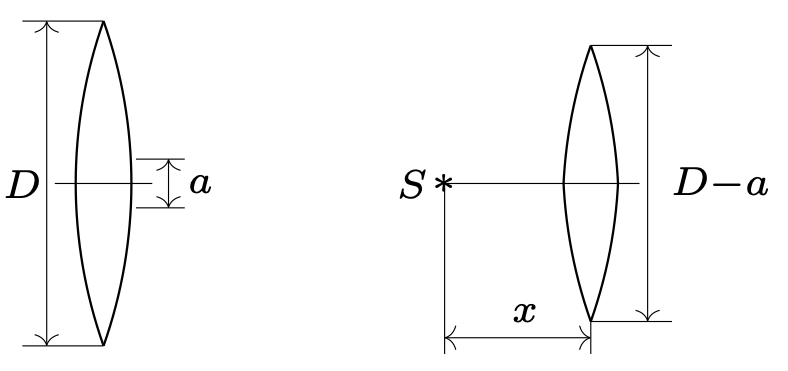
794. Z soczewki skupiającej o ogniskowej $f = 50$ cm i średnicy $D = 5$ cm wycięto środkowy pasek o szerokości 5 mm, a pozostałe części złożono ze sobą (rys. 1). W odległości $x = 75$ cm od soczewki umieszczono punktowe źródło światła monochromatycznego $S .$ Korzystając z przybliżenia małych kątów, znaleźć maksymalną liczbę prążków obrazu interferencyjnego, jaka może powstać na ekranie za soczewką. Długość fali świetlnej $λ = 5 \cdot 10^{- 7}$ m.

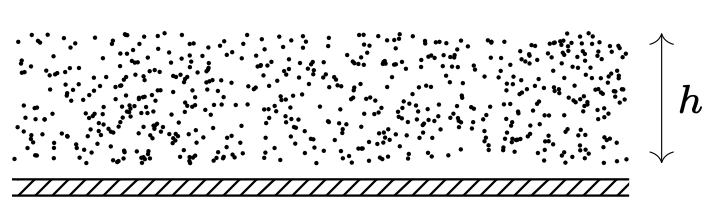
795. Izolowaną metalową początkowo nienaładowaną płytkę oświetlano w czasie $τ$ światłem nadfioletowym. W wyniku tego z płytki wyleciała chmura elektronów, których prędkość początkowa była prostopadła do płytki i miała wartość $v_{0} .$ Całkowita liczba elektronów, które wyleciały z jednostki powierzchni, wynosi $n,$ elektron ma ładunek $e$ i masę $m .$ Znaleźć grubość chmury $h$ po czasie $t$ od zakończenia naświetlania (rys. 2).

Rozwiązania zadań z numeru 11/2024

Przypominamy treść zadań:

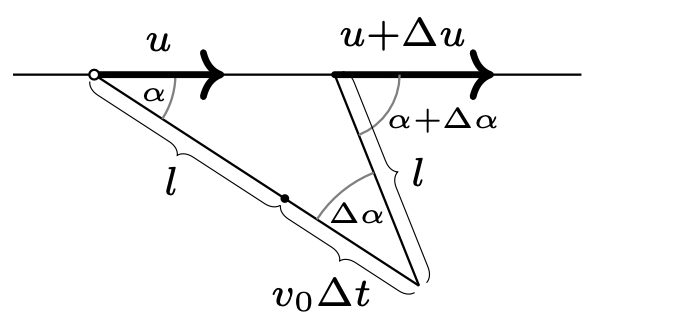
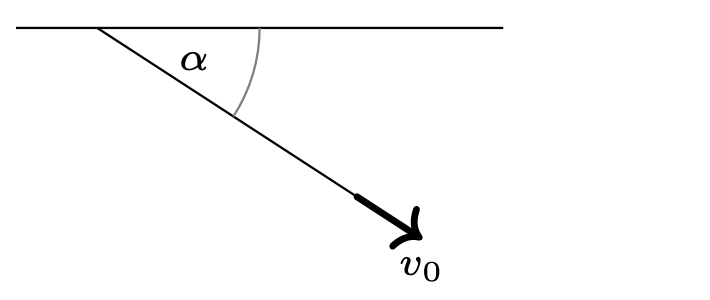
786. Koralik o masie $M$ może ślizgać się bez tarcia po prostym poziomym pręcie. Do koralika przywiązana jest lekka nierozciągliwa nitka o długości $l .$ Nitkę ciągniemy za swobodny koniec tak, że jego prędkość przez cały czas skierowana jest wzdłuż nitki i ma wartość $v_{0}$ (rys. 3). Jaką siłą ciągniemy w chwili, gdy nitka tworzy z prętem kąt $α$ ? Podczas ruchu nitka znajduje się w płaszczyźnie poziomej.

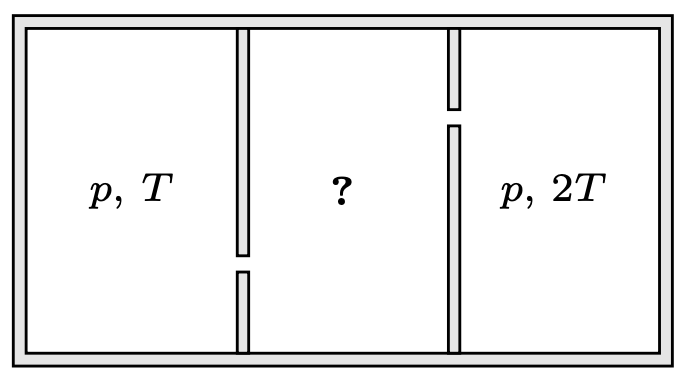
787. Nieprzewodzące ciepła naczynie połączone jest za pomocą dwóch małych jednakowych otworków z dwoma pojemnikami zawierającymi hel w stanie gazowym (rys. 4). W obu pojemnikach podtrzymywane jest jednakowe ciśnienie $p,$ w jednym z nich podtrzymywana jest temperatura $T,$ w drugim $2 T .$ Znaleźć ciśnienie i temperaturę w środkowym naczyniu w stanie równowagi.

786. Nić jest nierozciągliwa, zatem prędkości wszystkich jej punktów w danej chwili są jednakowe. Gdy kąt między nitką a prętem wynosi $α,$ prędkość koralika jest równa $u = v_{0} / \cos α .$ Jego przyspieszenie: $\begin{matrix} (1) & a = d u / d t = u \tan α (d α / d t) . \end{matrix}$ W małym przedziale czasowym $Δ t$ koralik przebywa drogę $u Δ t,$ koniec nici przemieszcza się o $v_{0} Δ t$ (rys. 5). Zgodnie z twierdzeniem sinusów $u Δ t / \sin (Δ α) = l / \sin α .$ Uwzględniając, że kąt $Δ α$ jest mały, otrzymujemy $d α / d t = u \sin α / l$ i zgodnie z $(1)$ $a = {(v_{0} \sin α)}^{2} / (l \cos^{3} α) .$ Szukana siła, jaką ciągniemy koralik, dana jest wzorem: $F = M a / \cos α = M (v_{0} \sin α)^{2} / (l \cos^{4} α) .$ 787. W stanie równowagi liczba cząsteczek w środkowym naczyniu nie zmienia się, czyli liczby cząsteczek wpadających do tego naczynia w jednostce czasu z lewej i prawej strony oraz opuszczających je są sobie równe: $\begin{matrix} (2) & N_{1} + N_{2} = N . \end{matrix}$ $N_{1}$ jest proporcjonalne do liczby cząsteczek w jednostce objętości $n_{1}$ w lewym naczyniu oraz do średniej prędkości ich ruchu cieplnego $v_{1},$ która z kolei jest proporcjonalna do $\sqrt{T} .$ Z równania Clapeyrona $n_{1} \sim p / T,$ zatem $N_{1} = α p / \sqrt{T},$ $α$ to współczynnik proporcjonalności. Analogicznie $N_{2} = α p / \sqrt{2 T},$

$N = 2 α p_{x} / \sqrt{T_{x}},$ gdzie $p_{x}$ jest szukanym ciśnieniem, a $T_{x}$ temperaturą w środkowym naczyniu. Podstawiając otrzymane wyrażenia do $(2)$ , otrzymujemy równanie: $\begin{matrix} (3) & p / \sqrt{T} + p / \sqrt{2 T} = 2 p_{x} / \sqrt{T_{x}} . \end{matrix}$ W stanie równowagi nie zmienia się również całkowita energia cząsteczek w środkowym pojemniku. Średnia energia przypadająca na cząsteczkę jest proporcjonalna do temperatury, zatem $N_{1} T + N_{2} 2 T = 2 N T_{x},$ $\begin{matrix} (4) & p \sqrt{T} + p \sqrt{2 T} = 2 p_{x} \sqrt{T_{x}} . \end{matrix}$ Rozwiązując układ równań $(3)$ , $(4)$ , otrzymujemy: $T_{x} = T \sqrt{2}, p_{x} = p (\sqrt{2} + 1) / 2 \sqrt[4]{2} .$