Afiliacja: Studentka, Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Algorytmy przeszukiwania grafów pojawiają się wszędzie. Bez nich nie działałaby Twoja ulubiona wyszukiwarka internetowa, a swoje „ścieżki w grafie” prawdopodobnie optymalizujesz podświadomie, na przykład planując swój dzień. Połączenia między Tobą, Twoimi przyjaciółmi i rodziną również tworzą graf, który gorączkowo przeszukujemy podczas spotkań towarzyskich.
Skoro algorytmy przeszukiwania grafów mają wiele zastosowań w codziennym życiu, nie powinno nas dziwić, że wiele zadań olimpijskich z matematyki można również rozwiązać, wykorzystując tę ideę.
Przeszukiwanie w głąb
Zanim przejdziemy dalej, omówmy najprostszy algorytm przeszukiwania grafów – przeszukiwanie w głąb, w skrócie DFS (depth first search).
Możemy o nim myśleć jak o „spacerze” po grafie. Podczas wykonywania algorytmu przechowujemy informację o tym, czy dany wierzchołek został już odwiedzony. Zaczynamy od wybrania wierzchołka początkowego. Kiedy w trakcie wykonywania algorytmu znajdziemy się w jakimś wierzchołku \(v,\) wykonujemy następujące instrukcje:
-
Oznacz wierzchołek \(v\) jako odwiedzony.
-
Dla każdego sąsiedniego wierzchołka \(u\) aktualnego wierzchołka \(v,\) jeśli \(u\) nie został jeszcze odwiedzony – rekurencyjnie wykonaj tę procedurę dla \(u.\)
-
Po zbadaniu wszystkich sąsiednich wierzchołków \(v\) wróć do poprzedniego wierzchołka – tego, z którego przyszliśmy do \(v.\)
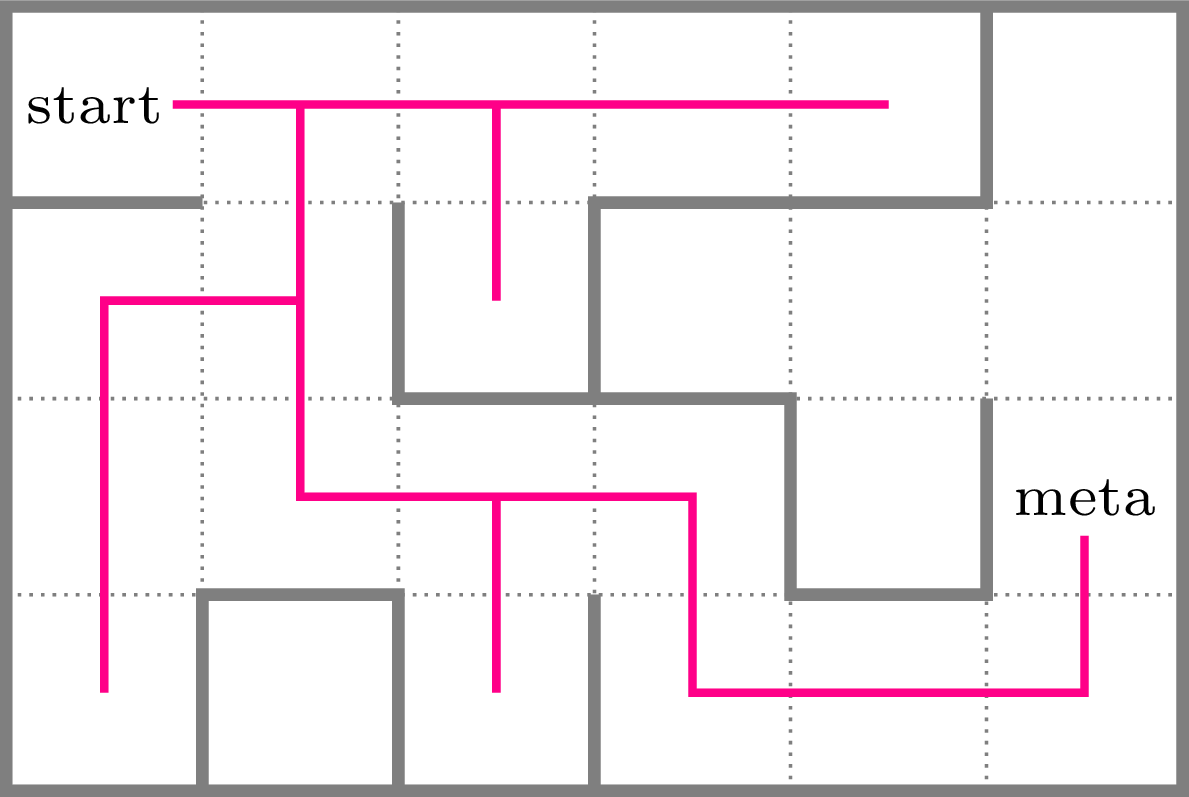
Pierwsza wersja przeszukiwania w głąb została wykorzystana w XIX wieku przez francuskiego matematyka Charlesa Pierre’a Trémaux jako strategia rozwiązywania labiryntów, jak ten poniżej. Komórki siatki można interpretować jako wierzchołki grafu. Krawędzie w grafie reprezentują wtedy możliwość ruchu, więc łączymy wierzchołki wtedy i tylko wtedy, gdy komórki reprezentowane przez te wierzchołki sąsiadują ze sobą bokiem.
O algorytmie DFS można myśleć analogicznie do zwiedzania. Wyobraź sobie, że jesteś turystą w tętniącym życiem mieście, trzymasz w rękach mapę i chcesz zobaczyć każdą ukrytą perełkę, jaką to miasto ma do zaoferowania. Zaczynasz od znanego muzeum, chłonąc sztukę i historię, po czym rozglądasz się za kolejnym, jeszcze nieodwiedzonym miejscem. Jeśli znajdziesz nową kawiarnię, urokliwą alejkę lub inny zabytek, udajesz się tam, ciesząc się nowymi widokami i dodając je do swojej „listy odwiedzonych miejsc”. Gdy dojdziesz do punktu, w którym wszystko w okolicy zostało zwiedzone, czas wrócić – cofnąć się do ostatniego miejsca, które miało jeszcze niezbadane ścieżki. Stamtąd kontynuujesz przygodę, odkrywając nowe ciekawostki i poruszając się naprzód, aż w pełni zwiedzisz wszystkie możliwe miejsca. Ta metoda zwiedzania zapewnia, że nie ominiesz żadnej lokalizacji. W końcu odwiedzisz całe miasto, nie pozostawiając żadnego zabytku nieodkrytym ani żadnego zakątka niezbadanym! W przypadku grafu spójnego dzieje się dokładnie to samo – po wykonaniu DFS stanie się on „całkowicie zwiedzony”. Łatwo zauważyć, że w czasie wykonywania algorytmu każdy wierzchołek ma trzy możliwe stany – albo nieodwiedzony (jeszcze nieosiągnięty przez DFS), odwiedzony (osiągnięty, ale nadal badany), albo całkowicie zbadany (wszyscy jego sąsiedzi zostali zbadani).
Powrót do zadań
Korzystając z algorytmu DFS, możemy podzielić krawędzie grafu na krawędzie drzewowe, zwane również krawędziami rozpinającymi (te, które są przechodzone podczas „spaceru”, tworząc ukorzenione drzewo rozpinające) oraz krawędzie wsteczne (pozostałe krawędzie, które zamykają cykle). Pomocne jest myślenie o krawędziach drzewowych jako skierowanych w dół, a o krawędziach wstecznych jako skierowanych w górę. Dlaczego takie podejście do analizy grafu jest pomocne? Aby to zobaczyć, udowodnijmy najważniejszą własność dotyczącą przeszukiwania grafu algorytmem DFS. Załóżmy, że mamy spójny graf \(G\) i wykonujemy DFS, zaczynając od dowolnego wierzchołka \(r.\)
Naszym celem jest pokazanie, że dla każdej krawędzi \((u, v)\) wierzchołek \(v\) jest albo przodkiem, albo potomkiem \(u\) w drzewie DFS – co oznacza, że \(v\) albo leży na ścieżce od \(u\) do korzenia \(r,\) albo znajduje się w poddrzewie \(u.\) Dlaczego tak jest? Załóżmy, że istnieje krawędź \((u, v)\) i bez utraty ogólności przeszukiwanie w głąb dotarło do \(u,\) podczas gdy \(v\) jest jeszcze nieodwiedzony. Wtedy:
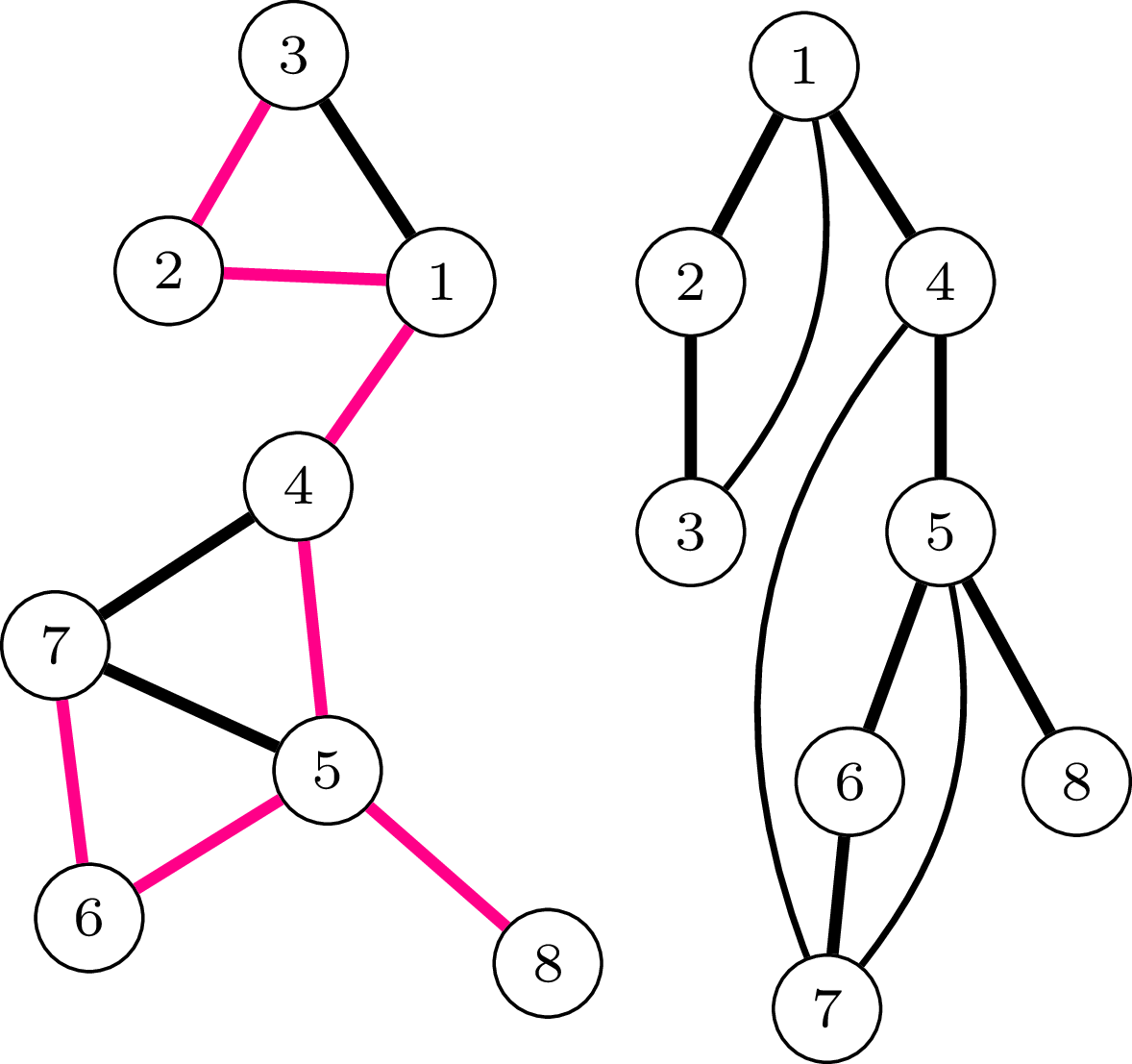
Na rysunku po lewej stonie mamy graf z \(8\) wierzchołkami. Załóżmy, że rozpoczynamy DFS w wierzchołku \(1.\) Jedna z możliwych tras może wyglądać następująco: \(1 \to 2 \to 3 \to 2 \to 1 \to 4 \to 5 \to\)
\(6 \to 7 \to 6 \to 5 \to 8 \to 5 \to 4 \to 1.\) Zauważmy, że gdyby istniała krawędź między \(3\) a \(4,\) to w tym przykładzie przeszlibyśmy z \(3\) do \(4,\) zamiast wrócić do \(2.\) Krawędzie, przez które przechodziliśmy do jeszcze nieodwiedzonego wierzchołka, tworzą drzewo rozpinające (te krawędzie są zaznaczone na czerwono na rysunku po lewej stronie). Rysunek po prawej stronie przedstawia ten sam graf z zaznaczonym ukorzenionym drzewem rozpinającym. Wszystkie dodatkowe krawędzie – nieużywane podczas przeszukiwania grafu – to krawędzie wsteczne.
-
Jeśli DFS przejdzie z \(u\) do \(v,\) używając \((u, v),\) to \((u, v)\) jest krawędzią drzewową.
-
Jeśli przeszukiwanie nie przejdzie do \(v\) z \(u,\) używając krawędzi \((u, v),\) to \(v\) musiało zostać już odwiedzone, gdy ta krawędź była rozważana. Mogło to się zdarzyć jedynie wtedy, gdy \(v\) zostało osiągnięte i zbadane wcześniej, podczas przeszukiwania jakiejś innej gałęzi wychodzącej z \(u.\)
W obu przypadkach \(v\) jest potomkiem \(u\) w drzewie DFS.
Kluczową zaletą drzewa DFS jest to, że upraszcza ono analizę grafu. Zamiast zajmować się wszystkimi rodzajami krawędzi, możemy skupić się na strukturze drzewa z kilkoma dodatkowymi krawędziami łączącymi przodków z potomkami. Dzięki temu graf staje się znacznie łatwiejszy do analizy.
Rozważmy następujące zadanie:
Zadanie: Niech \(G\) będzie spójnym, nieskierowanym grafem. Udowodnij, że krawędzie \(G\) można skierować w taki sposób, aby wynikowy graf był silnie spójny wtedy i tylko wtedy, gdy \(G\) nie ma mostów, tzn. krawędzi, których usunięcie rozspójnia graf.
Rozwiązanie: Jeśli \(G\) ma most \((u, v),\) skierowanie tej krawędzi od \(u\) do \(v\) (bez straty ogólności) oznacza, że nie istnieje ścieżka z \(v\) do \(u.\) Skupmy się więc teraz na drugiej implikacji.
Załóżmy, że \(G\) nie ma mostów. Wykonajmy DFS na grafie, zaczynając od dowolnego wierzchołka \(r.\) W wyniku tego algorytmu dostajemy ukorzenione drzewo rozpinające (wykorzystujące krawędzie drzewowe) oraz dodatkowe krawędzie wsteczne. Skierujmy krawędzie drzewowe w dół (od korzenia), a krawędzie wsteczne w górę (w kierunku korzenia). Aby udowodnić, że taki graf jest silnie spójny, wystarczy pokazać, że istnieje ścieżka skierowana od \(r\) do każdego wierzchołka oraz symetrycznie, że istnieje ścieżka od każdego wierzchołka do \(r.\) Pierwsza część jest łatwa – istnieje ścieżka wykorzystująca wyłącznie skierowane krawędzie drzewowe od \(r\) do każdego wierzchołka (ponieważ DFS odwiedził każdy wierzchołek).
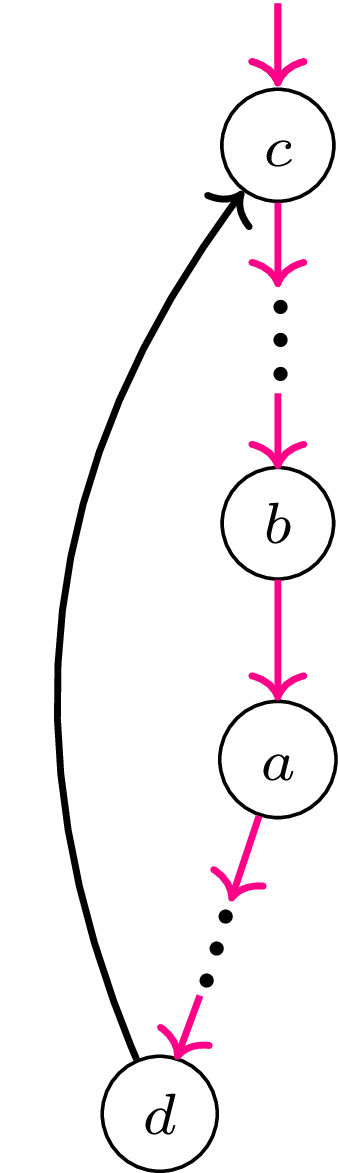
Zdefiniujmy głębokość wierzchołka \(v\) jako liczbę krawędzi drzewowych od korzenia \(r\) do \(v.\) Rozpatrzmy jakiś wierzchołek \(a\) różny od korzenia. Oczywiście w drzewie DFS istnieje krawędź \((b, a)\) łącząca \(a\) z jego rodzicem \(b.\) Ponieważ graf nie ma mostów, więc dla krawędzi drzewowej \((b, a)\) musi istnieć jakaś krawędź wsteczna \((d, c)\) łącząca pewien wierzchołek \(d\) z poddrzewa \(a\) (być może \(d = a\) ) z jakimś przodkiem \(c\) wierzchołka \(b\) (być może \(c = b\) ), bo gdyby taka nie istniała, krawędź \((b, a)\) byłaby mostem. Aby znaleźć ścieżkę od \(a\) do korzenia, poruszamy się z \(a\) do \(d\) za pomocą krawędzi drzewowych. Następnie przechodzimy krawędzią wsteczną z \(d\) do \(c.\) Ponieważ głębokość \(c\) jest mniejsza niż \(a,\) możemy powtarzać ten proces, aż dotrzemy do korzenia.
Zadanie (LXVII Olimpiada Matematyczna, etap drugi):
Dany jest spójny, nieskierowany graf z parzystą liczbą krawędzi.
Udowodnij, że jego krawędzie można połączyć w pary w taki sposób, że
każda para jest połączona ze sobą dokładnie jednym wierzchołkiem (innymi
słowy – takie pary tworzą ścieżkę długości dwa).
Rozwiązanie: Wykonajmy algorytm DFS na grafie, zaczynając od dowolnego wierzchołka \(r,\) i ponownie zdefiniujmy głębokość wierzchołka \(v\) jako liczbę krawędzi drzewowych od korzenia \(r\) do \(v.\) Przedstawimy kolejny algorytm przetwarzania wierzchołków. Po połączeniu w parę dwóch krawędzi możemy je usunąć. Na początku wszystkie wierzchołki są oznaczone jako nieprzetworzone:
-
Wybierz nieprzetworzony wierzchołek \(v\) o największej głębokości, który nie jest korzeniem.
-
Spójrz na krawędzie wychodzące z \(v,\) które nie zostały jeszcze usunięte. Są trzy typy takich krawędzi:
-
krawędzie wsteczne łączące \(v\) z jego przodkami,
-
krawędzie drzewowe łączące \(v\) z jego dziećmi,
-
jedna krawędź łącząca \(v\) z jego rodzicem przez krawędź drzewową.
Jeśli liczba nieusuniętych krawędzi jest parzysta, łączymy je w pary dowolnie i usuwamy wszystkie. W przeciwnym razie łączymy je w pary tak, aby pozostała tylko krawędź z \(v\) do jego rodzica.
-
-
Oznacz \(v\) jako przetworzony.
Pozostaje jeszcze połączyć w pary krawędzie wychodzące z \(r.\) Istnieje tylko jeden typ takich krawędzi – dzieci. Na początku graf miał parzystą liczbę krawędzi, a każda usunięta para składała się z parzystej liczby krawędzi (dokładnie dwóch). Zatem \(r\) ma parzystą liczbę dzieci i możemy je dowolnie połączyć w pary.
Teraz należy powiedzieć kilka słów o poprawności tej konstrukcji. Podczas rozważania wierzchołka \(v\) wierzchołki w jego poddrzewie są już przetworzone. Ponieważ w jednym kroku algorytmu usuwamy wszystkie dzieci wierzchołka, więc jedyne pozostałe krawędzie w poddrzewie \(v\) przed rozpoczęciem łączenia w pary muszą być dokładnie jego dziećmi i na pewno zostaną połączone w pary podczas przetwarzania \(v.\)
O specjalnym wierzchołku w drzewach
Każdy wie, czym są drzewa. Rosną w parkach (jakoś odwrócone – dlaczego korzeń jest na dole?) i na ogół są w każdym kierunku symetryczne – rzadko zdarza się, by jedna gałąź miała widocznie więcej liści i gałązek niż inne. Czy tak samo jest w przypadku drzew grafowych? Okazuje się, że tak. Bardziej formalnie, wykażemy, że w każdym drzewie z \(n\) wierzchołkami istnieje taki wierzchołek \(v,\) że jeśli ukorzenimy nasze drzewo w \(v,\) to każde jego poddrzewo będzie miało rozmiar co najwyżej \(\lfloor \frac{n}{2} \rfloor.\) Każdy taki wierzchołek nazywamy centroidem lub środkiem drzewa .
Postaramy się znaleźć taki wierzchołek w sposób rekurencyjny. Przypuśćmy, że ukorzeniliśmy nasze drzewo w pewnym wierzchołku \(r.\) Jeśli poddrzewa \(r\) mają rozmiar co najwyżej \(\lfloor \frac{n}{2} \rfloor,\) to mamy szczęście, ponieważ znaleźliśmy wierzchołek o żądanej własności. W przeciwnym razie musi istnieć taki wierzchołek \(w\) będący dzieckiem \(r,\) którego poddrzewo ma rozmiar większy niż \(\lfloor \frac{n}{2} \rfloor.\) Co więcej, taki wierzchołek musi być dokładnie jeden – gdyby istniały co najmniej dwa poddrzewa o rozmiarach \(s_1, s_2 > \lfloor \frac{n}{2} \rfloor,\) to mielibyśmy: \[n \geq s_1 + s_2 + 1 \geq 2\left(\left\lfloor \frac{n}{2} \right\rfloor+1\right) + 1 > n,\] więc rozmiar tych dwóch poddrzew wraz z korzeniem \(r\) przekroczyłby rozmiar całego drzewa! Analogicznie możemy wykazać, że jeśli poddrzewo \(w\) ma rozmiar większy niż \(\lfloor \frac n2 \rfloor,\) to po ukorzenieniu drzewa w wierzchołku \(w\) poddrzewo \(r\) będzie miało rozmiar co najwyżej \(\lfloor \frac n2 \rfloor.\)
W związku z tym możemy przejrzeć wszystkie sąsiednie wierzchołki \(r,\) a ponieważ \(w\) jest jedyny – rekurencyjnie sprawdzić, czy \(w\) jest dobrym kandydatem na centroid. Taki algorytm jest skończony, gdyż w każdym kroku rozmiar największego poddrzewa wierzchołka \(v\) się zmniejsza.
Zauważmy, że centroid nie musi być koniecznie jedyny. Na przykład w grafie składającym się z dwóch wierzchołków połączonych krawędzią oba wierzchołki są centroidami – każdy z nich ma jedno poddrzewo o rozmiarze \(1 = \frac{2}{1}.\) Z tego przykładu możemy wywnioskować, że drzewo ma dwa centroidy wtedy i tylko wtedy, gdy istnieje krawędź, której usunięcie dzieli drzewo na dwa mniejsze drzewa, każde o dokładnie \(\frac{n}{2}\) wierzchołkach (dowód pozostawiamy jako łatwe ćwiczenie).
Zadanie: Załóżmy, że w pewnym kraju, w którym będzie odbywał się obóz MBL, mamy \(n\) miast połączonych \(n-1\) drogami tworzącymi drzewo. Twoim zadaniem, jako organizatora obozu, jest efektywne zakwaterowanie uczestników. Przyjęto dokładnie \(2k\) osób z różnych miast \(v_1, \dots, v_{2k}.\) Podczas obozu uczestnicy utworzą pary (zespoły dwóch przyjaciół). Parowanie nie zostało jeszcze ustalone. Każda para będzie potrzebowała zakwaterowania. W każdym mieście znajduje się dokładnie jeden hotel. Uczestnicy z tej samej pary powinni zostać w tym samym hotelu (mogą być w nim także inne pary). Warunek, który musi zostać spełniony, jest następujący: jeśli osoby z miast \(u\) i \(w\) tworzą parę, ich hotel musi znajdować się w mieście na najkrótszej ścieżce łączącej \(u\) i \(w\) (może to być \(u\) lub \(w\) ). Ponieważ wynajęcie wielu hoteli w różnych miastach byłoby wyzwaniem organizacyjnym, połącz w pary uczestników tak, aby zminimalizować liczbę hoteli i spełnić powyższy warunek.
Szkic rozwiązania: W tym zadaniu mamy dane drzewo z \(2k\) specjalnymi wierzchołkami \(W = \{v_1, \dots, v_{2k}\}.\) Przypiszmy wagę każdemu wierzchołkowi: \({c_v = 1},\) jeśli \(v \in W,\) oraz \(0\) w przeciwnym razie. Jeśli znajdziemy taki wierzchołek \(v,\) że w każdym poddrzewie powstałym przez usunięcie \(v\) jest co najwyżej \(k\) specjalnych wierzchołków, to problem jest rozwiązany. Dlaczego? Ponieważ wówczas możemy zachłannie łączyć w pary wierzchołki z różnych poddrzew powstałych przez usunięcie \(v\) z największą liczbą specjalnych punktów, a ścieżki między nimi zawsze będą przechodziły przez \(v.\) Pozostaje pytanie – jak znaleźć taki wierzchołek \(v\) ? Definicja \(v\) przypomina definicję centroidu – zamiast obliczać rozmiar poddrzewa, będziemy obliczać sumę wag w poddrzewie. Wówczas algorytm znajdowania centroidu znajdzie również nasz wierzchołek \(v.\) W związku z tym dochodzimy do wniosku, że zawsze wystarczy wynająć jeden hotel.
Kolejne zadanie, tym razem pozostawione jako ćwiczenie dla Czytelnika:
Zadanie (na podstawie zadania z drugiego etapu XXX Olimpiady Informatycznej): Antek i Marysia grają w grę na drzewie. Początkowo wszystkie wierzchołki są białe, z wyjątkiem jednego wierzchołka \(x,\) który jest czerwony (należy do Antka), oraz innego wierzchołka \(y,\) który jest niebieski (należy do Marysi). Każdy z graczy na zmianę wybiera dowolny wierzchołek \(u\) w swoim kolorze i koloruje sąsiedni biały wierzchołek \(v\) na swój kolor. Gracz, który nie może wykonać ruchu, przegrywa grę. Określ, kto ma strategię wygrywającą w zależności od początkowych pozycji \(x\) i \(y\) Antka i Marysi.
Podsumowanie
Jak mogliśmy zobaczyć, istnieje wiele zastosowań algorytmu DFS i centroidów w problemach olimpijskich z matematyki. Jednak DFS to znacznie więcej – używamy algorytmów przeszukiwania grafu niemal nieustannie, nawet nie zdając sobie z tego sprawy! Następnym razem, gdy będziesz rozwiązywać sudoku lub spieszyć się do szkoły czy pracy, pamiętaj, że w rzeczywistości rekurencyjnie podążasz jakąś ścieżką w grafie, mając nadzieję, że znajdziesz tę właściwą.