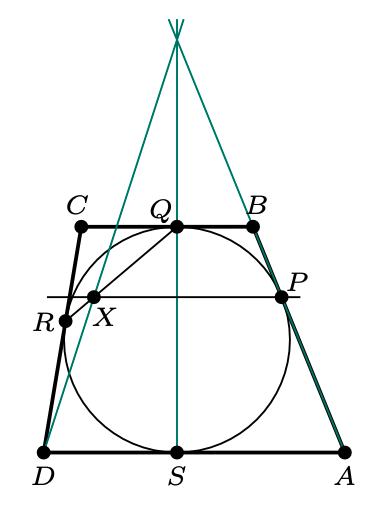
Niech \(ABCD\) będzie trapezem \((DA\!\parallel \! CB)\) opisanym na okręgu, który jest styczny do boków \(AB,\) \(BC,\) \(CD\) i \(AD\) odpowiednio w punktach \(P,\) \(Q,\) \(R,\) \(S.\) Prosta przechodząca przez \(P\) i równoległa do podstaw trapezu przecina prostą \(QR\) w punkcie \(X.\) Udowodnić, że proste \(AB,\) \(QS\) i \(DX\) przecinają się w jednym punkcie.
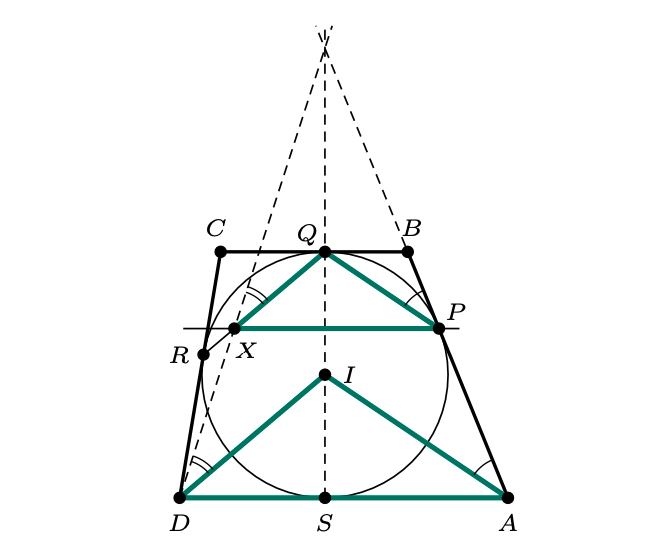
Niech \(I\) będzie środkiem okręgu wpisanego w rozważany trapez. Wówczas \[\measuredangle IAP=\frac{1}{2}\measuredangle DAB=\frac{1}{2}(180^{\circ}-\measuredangle ABC) =\measuredangle QPB,\] stąd \(PQ\!\parallel \! AI.\) Podobnie \(DI\parallel QR,\) więc trójkąty \(ADI\) oraz \(PXQ\) mają odpowiednie boki równoległe, a więc są jednokładne. Środek tej jednokładności jest punktem przecięcia prostych \(AB,\) \(QS\) i \(DX.\)
Dane są liczby \(a,\) \(b>1,\) dla których \[a+\frac{1}{a^2} \geq 5b-\frac{3}{b^2}.\] Udowodnić, że \(\displaystyle a>5b-\frac{4}{b^2}.\)
Dane są liczby całkowite \(n>20\) i \(k>1\) takie, że \(k^2\mid n.\) Udowodnić, że istnieją dodatnie liczby całkowite \(a,\) \(b,\) \(c,\) dla których \[n=ab+bc+ca.\]
-
\(m+1>p.\) Możemy wtedy wziąć \(a=p,\) gdyż \(n+a^2=p^2\cdot (m+1)\) i zarówno \(p^2,\) jak i \(m+1\) są większe od \(a.\)
-
\(m+1<p\) i \(m+1\) jest liczbą złożoną. Niech \(m+1=st\) dla pewnych liczb całkowitych \(s,t>1.\) Znów możemy przyjąć \(a=p,\) gdyż \(n+a^2=ps\cdot pt\) i obie liczby \(ps\) i \(pt\) są większe od \(a.\)
-
\(m+1<p\) i \(m+1\) jest liczbą pierwszą. Niech \(m+1=q\) i podzielmy \(p\) przez \(q\) z resztą: \(p=\ell q+r,\) gdzie \(r>0.\) Weźmy \(a=r,\) wtedy \(n+a^2=q\cdot (\ell^2mq+2\ell m r+r^2)\) i oba czynniki są większe od \(r.\)
-
\(m+1=p.\) Wtedy oczywiście \(n=p^3-p^2>20,\) więc możemy założyć, że \(p\geq 4.\) Zachodzi \[n+6^2=(p+3)\cdot (p^2-4p+12),\] przy czym oba czynniki po prawej stronie są większe od 6.
W każdym z przypadków dostaliśmy żądany rozkład, więc teza zadania została udowodniona.
W szczelnie zamkniętm cylindrze, pod tłokiem znajduje się \(m = 10\) g ciekłej wody. Bardzo szybkie przesunięcie tłoka powoduje spadek ciśnienia w cylindrze do wartości bliskiej zeru. Temperatura otoczenia i cylindra z wodą wynosi 0. Ile lodu wytworzy się w wyniku tego procesu? Można przyjąć, że początkowo pod tłokiem była wyłącznie ciekła woda. Ciepło topnienia wody \(L_f \approx 334\) J/g, a ciepło parowania \(L_v \approx 2260\) J/g.
W szczelnym pojemniku znajduje się mieszanina helu i neonu. Mieszanina jest w równowadze termodynamicznej, przy czym liczby moli neonu i helu są takie same. W sciance pojemnika zrobiono bardzo mały otwór. Jaki będzie skład wiązki gazu uchodzącego z pojemnika tuż po wykonaniu otworu? W jednostkach masy atomowej masy atomowe wynoszą: helu \(\mu_{\rm He} = 4,\) a neonu \({\mu_{\rm Ne} = 20}.\)