Afiliacja: Wydział Chemiczny, Politechnika Śląska w Gliwicach
O tym, że asysta grawitacyjna jest często wykorzystywana podczas rozpędzania pojazdów kosmicznych, słyszał zapewne każdy miłośnik astronautyki. Wiele sond kosmicznych, szczególnie tych skierowanych w odległe zakątki Układu Słonecznego, korzysta z tej metody powiększania prędkości. Technika ta jest doskonałym przykładem zastosowania orbit hiperbolicznych w astronomii (ściślej – w astrodynamice, nauce zajmującej się orbitami sztucznych pojazdów kosmicznych). Niestety, jej szczegóły rachunkowe nie są powszechnie omawiane w podręcznikach fizyki ogólnej czy nawet w podręcznikach astronomii – dlatego zajmiemy się nimi w poniższym artykule.
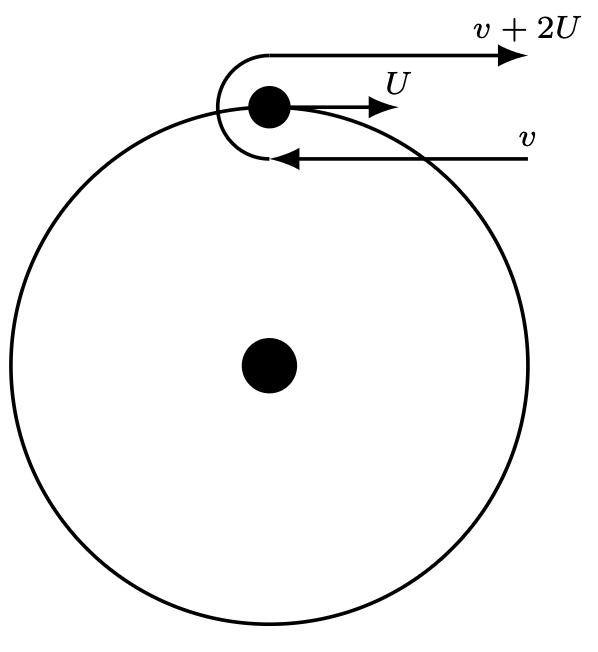
Rys. 1. Manewr asysty grawitacyjnej wokół planety. Planeta porusza się z prędkością \(U\) względem Słońca, a prędkość pojazdu względem Słońca jest równa \(v\)
Podstawowa idea asysty grawitacyjnej wydaje się bardzo prosta. Na rysunku 1 widać, jak pojazd kosmiczny poruszający się z prędkością \(v\) wchodzi tymczasowo na orbitę planety poruszającej się z prędkością \(U.\) Porusza się wokół niej po półorbicie (\(180^\circ\)) z prędkością \(v+U\) względem planety, aby następnie opuścić ją z tą samą prędkością \(v+U\) (względem planety), lecz w przeciwnym kierunku. Względem nieruchomego obserwatora – np. na Słońcu, prędkość ta będzie powiększona o prędkość planety \(U,\) dając \(v+2U.\)
Wszystko pięknie, tylko… Jak to zrobić, żeby pojazd kosmiczny „częściowo” orbitował wokół planety? I jak kontrolować to, w którym miejscu pojazd wchodzi na orbitę, a w którym z niej wychodzi? Aby rozwiązać ten problem, musimy posłużyć się modelem orbit otwartych, a więc orbit hiperbolicznych (lub parabolicznych, ale w artykule skupimy się na tych pierwszych).
Kąt ugięcia trajektorii
Zajmiemy się najpierw wyznaczeniem kąta ugięcia trajektorii pojazdu kosmicznego. Wspomagając się rysunkiem 2, widzimy, że rzut prędkości na oś symetrii zmienia znak przy ugięciu i przechodzi od \({v \cos(180^\circ - \theta_0)}\) (zwróconego w kierunku prawego górnego rogu) do \({-v \cos(180^\circ - \theta_0)},\) gdzie \(v\) to długość wektorów \(v_{\textrm{in}}\) i \(v_{\textrm{out}}.\) Ponieważ \({\cos(180^\circ - \theta_0) = -\cos\theta_0},\) więc: \[\Delta v = 2v \cos\theta_0.\] Tę składową prędkości można również wyznaczyć z przyspieszenia, działającego w żądanym kierunku. Wówczas, korzystając z prawa grawitacji Newtona, w krótkim czasie \(\delta t\) prędkość zmienia się o \(\delta v\) dane wzorem: \[\delta v = -\frac{GM}{r^2} \cos\theta \, \delta t.\] Aby uzyskać \(\Delta v,\) sumujemy infinitezymalne przyrosty \(\delta v\) dla możliwych wartości \(t\): \[\Delta v = \sum_{t = -\infty}^{+\infty} -\frac{GM}{r^2} \cos\theta \, \delta t,\] przy czym znak „\(-\)” wynika z faktu, że siła grawitacji działa w kierunku planety i zarazem odwrotnie do przyjętego kierunku prędkości (prawego górnego rogu rysunku).
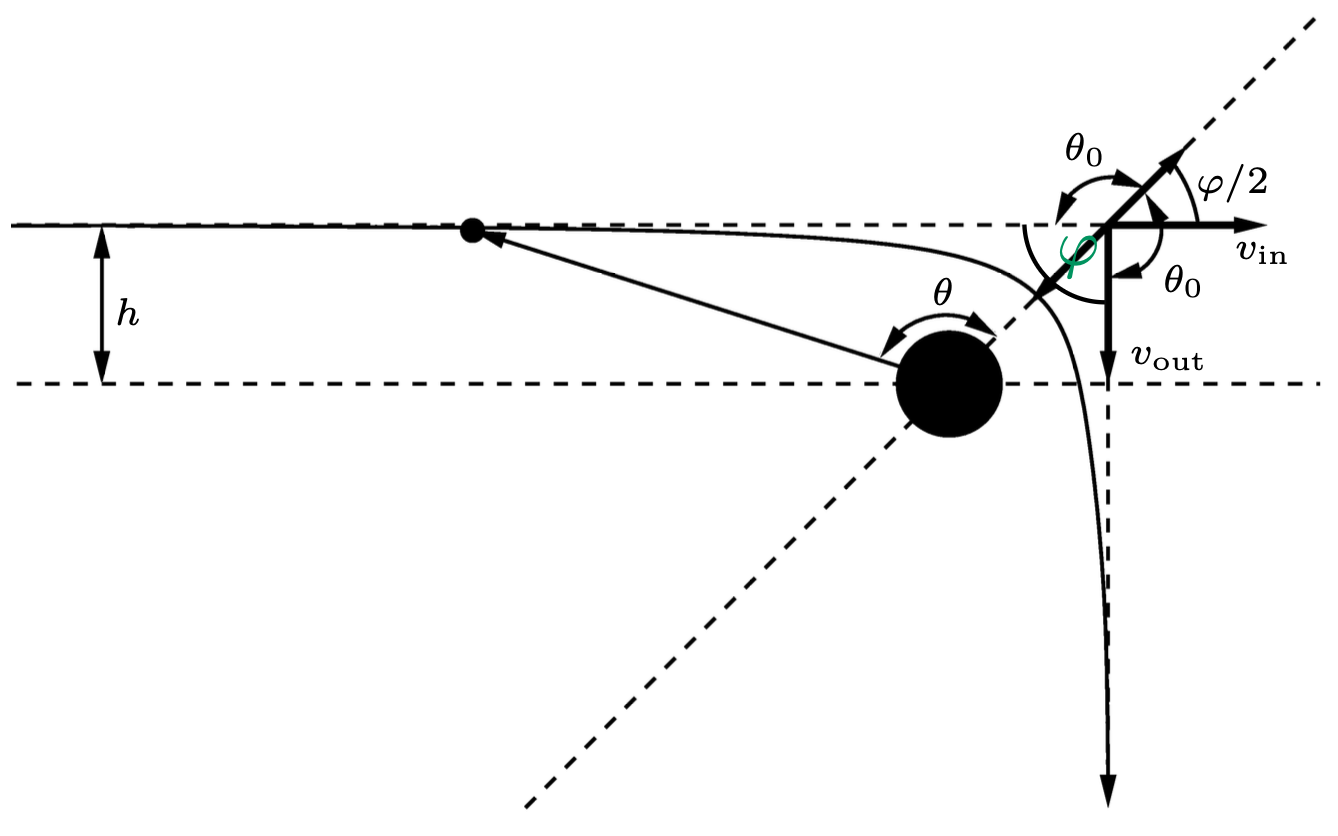
Rys. 2. Kąt ugięcia trajektorii pojazdu kosmicznego korzystającego z asysty grawitacyjnej
Sumowanie po czasie zamienimy teraz na łatwiejsze sumowanie po kącie \(\theta.\) Wyraźmy najpierw przyrost czasu \(\delta t\) poprzez przyrost kąta: zakładając chwilową prędkość kątową \(\omega,\) mamy \(\delta t = \frac{\delta \theta}{\omega}.\) Z mechaniki klasycznej dla ruchu centralnego moment pędu spełnia równość \({J = I\omega = mr^2 \omega},\) co daje: \[\omega = \frac{J}{mr^2} \ \ \ \Longrightarrow \ \ \ \delta t = \frac{mr^2}{J} \, \delta\theta.\] Podstawiając do wzoru na przyrost prędkości, dostajemy: \[\delta v = -\frac{GM}{r^2} \cos\theta \cdot \frac{mr^2}{J} \, \delta\theta = -\frac{GMm}{J} \cos\theta \, \delta\theta,\] a po wysumowaniu po kącie \(\theta\): \[\Delta v = \sum_{\theta = -\theta_0}^{+\theta_0} -\frac{GMm}{J} \cos\theta \, \delta\theta.\]
Dla Czytelników, którzy nie znają metody całkowania, wyjaśniamy: podane wyrażenie opisuje pole pod wykresem funkcji \(\cos \theta,\) ograniczone przedziałem od \(-\theta_0\) do \(\theta_0.\) Każdy składnik sumy to pole prostokąta o podstawie \(\delta \theta\) i wysokości \(\cos\theta.\)
Zachęcamy także do samodzielnego wyprowadzenia tego faktu, z wykorzystaniem definicji pochodnej: \(f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}\) oraz faktu, że pochodną funkcji sinus jest cosinus.
Dla bardzo małych \(\delta\theta\) możemy skorzystać z faktu: \[\lim_{\delta \theta \rightarrow 0}\sum_{\theta = -\theta_0}^{+\theta_0} \cos\theta \, \delta\theta = \int_{-\theta_0}^{+\theta_0} \cos\theta \, d\theta = 2\sin \theta_0,\] co daje nam: \[\Delta v \approx -\frac{2GMm}{J} \sin\theta_0.\] W powyższym równaniu musimy jeszcze obliczyć moment pędu \(\vec J = \vec r \times m \vec v.\) Jest on zachowany w całej trajektorii i najłatwiej go wyznaczyć w dużej odległości od ciała niebieskiego, gdzie prędkość nie została jeszcze zmieniona przez grawitację. Po podstawieniu \(r\sin\theta = h\) (odległość planety od asymptoty hiperboli) dostajemy \(J = mvh,\) a wzór na zmianę prędkości przechodzi w: \[\Delta v = -\frac{2GM}{hv} \sin\theta_0.\] Porównując z wcześniejszym wyrażeniem na zmianę prędkości: \[2v \cos\theta_0 = -\frac{2GM}{hv} \sin\theta_0,\] otrzymujemy zależność: \[\tan\theta_0 = -\frac{hv^2}{GM}, \ \ \ \Longrightarrow \ \ \ \cot\biggl(\frac{\varphi}{2}\biggr) = \frac{hv^2}{GM}. \tag{$*$}\] Wartość \(\varphi\) to kąt ugięcia trajektorii pojazdu kosmicznego, a \(\theta_0 = 90^\circ + \frac{\varphi}{2}\) (rys. 2). Przesunięty tangens jest kotangensem z minusem, stąd wynik \((*).\)
Maksymalne zbliżenie do planety
Parametr zderzenia \(h,\) tj. odległość, w jakiej „asymptotycznie” chcemy przelecieć obok planety, zawsze jest większy niż minimalna odległość, w jakiej pojazd kosmiczny mija planetę, na której podlega asyście grawitacyjnej. Aby uniknąć zderzenia, warto zatem mieć możliwość obliczenia minimalnej odległości, na jaką pojazd zbliża się do planety. W tym celu zapisujemy: \[E = \frac{mv_r^2}{2} + \frac{J^2}{2mr^2} - \frac{GMm}{r}.\] Czyli: na energię pojazdu kosmicznego składa się jego energia kinetyczna związana z ruchem w kierunku planety (opisywana przez składową radialną prędkości \(v_r\)), energia ruchu obrotowego (\(J^2/2mr^2\)) oraz energia potencjalna grawitacji. Kiedy pojazd jest bardzo daleko od planety, jego energia potencjalna jest praktycznie równa zero, a więc jego energia i moment pędu dane są wtedy przez \(E=mv^2/2,\) \(J=mvh.\) Przy maksymalnym zbliżeniu składowa radialna prędkości jest równa zero i korzystając z zasad zachowania energii i zachowania momentu pędu (\(E\) i \(J\) są stałe), dostajemy: \[\frac{mv^2}{2} = \frac{1}{2}mv^2h^2 \frac{1}{r_{\text{min}}^2} - \frac{GMm}{r_{\text{min}}}, \ \ \ v^2 r_{\text{min}}^2 + 2GM r_{\text{min}} - v^2 h^2 = 0,\] i po rozwiązaniu równania kwadratowego: \[r_{\text{min}} = \frac{-GM}{v^2} \left(1 - \sqrt{1 + \frac{v^4 h^2}{G^2 M^2}}\,\right) = \frac{GM}{v^2} \left(\sqrt{1 + \frac{v^4 h^2}{G^2 M^2}} - 1\,\right).\]
To równanie możemy również zapisać w bardziej zwartej formie, porównując je z równaniem hiperboli we współrzędnych biegunowych (patrz: dodatkowy materiał w wersji elektronicznej artykułu). Wówczas widzimy, że \(r_{\text{min}} = a(e-1),\) przy czym \(a = \frac{GM}{v_0^2}\) to połowa odległości między ogniskami hiperboli, natomiast \(e=\sqrt{1 + \frac{v_0^4 h^2}{G^2 M^2}}\) to jej mimośród. Takie przedstawienie równania pozwala uniknąć błędów związanych z operowaniem bardzo rozbudowaną formułą.
Asysta grawitacyjna Voyagera 1 z 5 marca 1979 roku
Voyager 1 wykonał asystę grawitacyjną wokół Jowisza (\(GM = 1{,}27 \cdot 10^8\, \text{km}^3/\text{s}^2\)). Do planety podchodził z prędkością \(v_0 = 10{,}8\,\text{km/s}\) (względem planety) i zbliżył się na odległość \(3{,}48 \cdot 10^5\,\text{km}.\) Kąt wektora prędkości sondy do wektora prędkości planety przed ugięciem wynosił \(\varphi = 180^\circ - 63{,}8^\circ = 116{,}2^\circ.\)
Zadanie: Obliczyć kąt ugięcia trajektorii oraz parametr zderzenia. Jakie były prędkości względem Słońca przed i po zderzeniu?
Rozwiązanie:
Aby wyznaczyć parametr zderzenia, korzystamy ze wzoru na marginesie \({r_{\text{min}} = a(e-1)}\):
\[\begin{aligned}
a = \frac{GM}{v_0^2} = 1{,}09 \cdot 10^6\, \text{km} \ \ \ & \Longrightarrow \ \ \ e = \frac{r_{\min}}{a} + 1 = 1{,}319
\\
&
\Longrightarrow \ \ \ h = \frac{GM}{v_0^2} \sqrt{e^2 - 1} = 9{,}38 \cdot 10^5\, \text{km}.
\end{aligned}\]
Dysponując \(h\) (zwróćmy uwagę, że jest ono blisko 3 razy większe niż \(r_{\min}\)), łatwo obliczyć kąt ugięcia trajektorii \(\varphi\) z \((*)\):
\[\varphi = 2 \operatorname{arcctg} \left( \frac{h v_0^2}{GM} \right) = 98{,}6^\circ.\]
Aby określić prędkości względem Słońca przed (\(v_i\)) i po zderzeniu (\(v_f\)), rozkładamy prędkość w układzie planety na styczną i prostopadłą do prędkości planety i część styczną uzupełniamy o prędkość planety (\(12{,}83\, \text{km/s}\)):
\[\begin{aligned}
v_i & = \sqrt{\underbrace{v_0^2 \sin^2 \varphi}_{\text{prędkość prostopadła}} + \underbrace{(v_0 \cos \varphi + 12{,}83\, \text{km/s})^2}_\text{prędkość styczna}} = 12{,}593\, \text{km/s},
\\
v_f & = \sqrt{\underbrace{v_0^2 \sin^2 (\varphi - \Phi)}_{\text{prędkość prostopadła}} + \underbrace{(v_0 \cos (\varphi - \Phi) + 12{,}83\, \text{km/s})^2}_\text{prędkość styczna}} = 23{,}324\, \text{km/s}.
\end{aligned}\]
Parametry innych asyst dla Voyagera 1 i Voyagera 2
Literatura
R.J. Cesarone, „A gravity assist primer”, AIAA Student Journal, 1989.
R.R. Bate, D.D. Mueller, J.E. White, „Fundamentals of astrodynamics”, Dover, 1971.
J. Biney, S. Tremaine, „Galactic dynamics”, Princeton University Press, 2008.
N. Harnew, „Classical Mechanics: open orbits”, wykład, Oxford, 2017.
S. Charzyński, „Proca grawitacyjna”, Delta 7, 2014.
David (Hop) Hollister, „Conic Sections & Celestial Mechanics” Coloring Book (Az Publishing, 2011).
Na koniec, by dać możliwość dodatkowego przećwiczenia przedstawionej wiedzy, podajemy tabelę z danymi dotyczącymi manewrów sond Voyager 1 i Voyager 2.
| Misja | \(r_{\text{min}}\) [km] | \(v_0\) [km/s] | \(GM\) [km3/s2] | \(v_B\) [km/s] | \(\varphi\) |
|---|---|---|---|---|---|
| Voyager 1, Jowisz | \(3{{,}}48\times10^5\) | 10,8 | \(1{{,}}27\times10^8\) | 12,8 | 116\(^\circ\) |
| Voyager 2, Jowisz | \(7{{,}}21\times10^5\) | 7,62 | \(1{{,}}27\times10^8\) | 12,7 | 132\(^\circ\) |
| Voyager 2, Saturn | \(1{{,}}61\times10^5\) | 10,7 | \(3{{,}}79\times10^7\) | 9,59 | 81,8\(^\circ\) |
| Voyager 2, Uran | \(1{{,}}07\times10^5\) | 14,7 | \(5{{,}}79\times10^6\) | 6,71 | 74\(^\circ\) |
Źródło: R.J. Cesarone (1989). W oryginalnym artykule kąty podawane były względem grotu prędkości planety, tu są przeliczone na kąt między wektorami zaczepionymi we wspólnym punkcie.
Uwaga: prędkości planet wykazują różnice w różnych miejscach swojej orbity!
Załącznik: Biegunowa postać równania hiperboli (pdf)