Starożytna cywilizacja stworzona przez Majów słynie z doniosłych wynalazków i odkryć. Majowie potrafili z niesamowitą precyzją przewidywać różne zjawiska astronomiczne – i to na długo przed wynalezieniem lunety, nie mówiąc już o teleskopie. W tym artykule omówimy podstawy aparatu matematycznego, który wykorzystywali do swoich dokonań. Wyruszmy więc w podróż do odległych czasów, kiedy na terenach dzisiejszego Meksyku, Gwatemali, Belize, Hondurasu oraz Salwadoru kwitła cywilizacja Majów. Ich ziemie, usiane majestatycznymi górami i gęstymi dżunglami, były areną niezwykłych osiągnięć w dziedzinie astronomii, matematyki, architektury oraz pisma hieroglificznego.
Kalendarze Majów
Spośród wszystkich mieszkańców Mezoameryki to właśnie Majowie wykazali się największym wyrafinowaniem w dziedzinie pomiaru czasu. Podstawową jednostką czasu był dla nich K’in (dzień). Dwadzieścia K’inów to Winal (miesiąc). Tun (rok) to 360 K’inów, to znaczy 18 Winali. Natomiast 20 Tunów, czyli 20 lat, daje 1 K’atun (7200 K’inów). Baktun to najdłuższy okres u Majów, odpowiada 20 K’atunom (144 000 K’inów).
W związku z tym datę Majowie określali, używając pięciu liczb – na liczbę K’inów, Winali, Tunów, K’atunów i Baktunów. Każda z nich należała do przedziału od 0 do 19, za wyjątkiem liczby Winali – ta przyjmowała wartości od 0 do 17, ponieważ 18 Winali składało się na jeden Tun. Majowie zapisywali te liczby od góry do dołu lub od lewej do prawej, korzystając z systemu specjalnych znaków zwanych glifami.
Majowie opracowali również bardzo skomplikowany system chronologiczny, składający się z czterech kalendarzy. Były to Tzolkin, Haab, Kalendarz Księżycowy oraz Długi Kalendarz (DK).
Pierwszy z nich, Tzolkin, to 260-dniowy kalendarz rytualny, używany przy ceremoniach i planowaniu wojen. Podzielony jest on na 13 miesięcy, każdy po 20 dni. Drugim jest Haab – 365-dniowy kalendarz słoneczny, podzielony na 18 miesięcy, każdy po 20 dni, po których następuje dodatkowy 5-dniowy okres nazywany Wayeb. Trzecim kalendarzem jest 9-dniowy kalendarz księżycowy, zwany kalendarzem Dziewięciu Władców Nocy. Ostatni kalendarz nazwany jest Długim (DK), gdyż zawierał 52 okresy po 365 dni. Służył do rejestrowania wydarzeń – pozwalał na precyzyjne określanie dat sięgających tysięcy lat wstecz. To, że Długi Kalendarz trwał dokładnie ten czas, nie jest przypadkiem – jest to najmniejsza wspólna wielokrotność długości Tzolkina (260 dni) i Haaba (365 dni). Okres ten nazywany jest „okręgiem kalendarzowym”.
Co to za baza?
Majowie do obliczeń matematycznych używali systemu liczbowego opartego na bazie \(20.\) Przy użyciu tej bazy każda liczba \(n\in \mathbb{N}\) jest przedstawiona jako: \[n=\sum_{p=0}^m a_p\times 20^p, \ \ \ m\in \mathbb{N}.\] Innymi słowy, w systemie opartym na bazie \(20\) dla każdej liczby:
jej pierwsza pozycja (w zapisie Majów to pozycja dolna) reprezentuje wartości od 0 do 19 (dla \(20^0\));
druga pozycja – wartości od 0 do 19, każda reprezentująca wielokrotność 20 (= \(20^1\));
trzecia pozycja – wartości od 0 do 19, każda reprezentująca wielokrotność 400 (= \(20^2\)) i tak dalej.
W systemie liczbowym o podstawie \(20\) mamy łącznie \(20\) cyfr, które służą do zapisywania wszystkich liczb. Pierwsze dziesięć cyfr to te, które znamy z systemu dziesiętnego: \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9.\) Aby uniknąć pomyłek i niejasności, do oznaczania liczb od \(10\) do \(19\) (które w bazie \(20\) są w zasadzie cyframi) będziemy używać liter – \(10\) zapisywane jest jako \(A,\) \(11\) jako \(B\) i tak dalej aż do \(19\) jako \(J.\) Zobaczmy przykładowe działania w tym systemie:
Czy wiesz, czemu odpowiada liczba \(AA\) w bazie \(10\) i jak zapisać jej rozkład na czynniki pierwsze w bazie \(10\) i \(20\)?
\(2\times 5\) daje wynik odpowiadający cyfrze \(A\) (czyli 10 w naszym systemie),
\(6\times 7\) przedstawia się jako \(2\times 20+2\) (co zapisać można jako 22 w bazie 20).
System chronologiczny
Majowie używali również innego, specjalnego systemu liczbowego (system chronologiczny), dostosowanego do zapisu dat w ich kalendarzach. W systemie chronologicznym trzecia pozycja różni się od standardowego wzorca, ponieważ reprezentuje wielokrotność 360 \((=18 \times 20)\), a nie 400 \((=20^2)\). Wynika to z dostosowania do kalendarza Haab’, który składał się z 18 miesięcy po 20 dni, co daje 360 dni. Dzięki temu odpowiada ona liczbie dni w roku kalendarzowym Majów, co ułatwiało obliczenia dat.
W systemie chronologicznym kalendarza Majów liczba jest więc zapisana jako: \[n= a_0\times 20^0+ a_1\times 20^1 + a_2\times 18 \times 20 + a_3\times 18 \times 20^2+\cdots.\] Rozważmy przykład daty \([8;14;3;1;12]\) zapisanej w Długim Kalendarzu.
| Jednostka | Liczba | Dni na jednostkę | Razem dni |
|---|---|---|---|
| Baktun | 8 | 144 000 | \(8 \times 144\,000 = {1\,152\,000}\) |
| K’atun | 14 | 7 200 | \(14 \times 7\,200 = {100\,800}\) |
| Tun | 3 | 360 | \(3 \times 360 = {1080}\) |
| Winal | 1 | 20 | \(1 \times 20 = {20}\) |
| K’in | 12 | 1 | \(12 \times 1 = {12}\) |
| Suma całkowita | \(\mathbf{{1\,253\,912}}\) | ||
Długi Kalendarz zaczyna się od mitycznej daty, która jest odpowiednikiem 11 sierpnia 3114 roku p.n.e. w naszym kalendarzu (kalendarz gregoriański). Aby przeliczyć datę \([8;14;3;1;12]\) na datę gregoriańską, dodajemy \(1\,253\, 912\) dni do 11 sierpnia 3114 roku p.n.e. Po obliczeniu otrzymujemy datę w kalendarzu gregoriańskim: 15 września 320 roku n.e.
Czy wiesz, jak zapisać dzisiejszą datę w kalendarzu Majów?
Jak zapisać liczby glifami ?
Majowie nie znali cyfr arabskich (którymi posługujemy się dzisiaj). W ich systemie:
1 kropka = 1 jednostka,
1 kreska = 5 jednostek,
specjalny symbol w kształcie muszli reprezentuje zero.
Nadmieńmy tutaj, że wprowadzenie zera jest niezwykłym osiągnięciem – cyfra ta dotarła do Europy dopiero w jedenastym wieku.
Zapis Majów 31 \(\scriptstyle\bullet\) \(1 \times 20\) \(+\) \(\stackrel{\bullet}{\boldsymbol{=}}\) \(11\)
W systemie Majów liczba 31 zapisywana była jako „jeden razy dwadzieścia” \((1\times 20)\) plus 11. W zapisie glifami \(11\) to dwie kreski ułożone jedna nad drugą plus jedna kropka nad najwyższą kreską, a żeby dodać do tego \(1 \cdot 20,\) musimy dopisać jeszcze jedną kropkę powyżej.
Pokażmy jeszcze inne przykłady: Majowie zapisywali 7 jako kreskę (czyli 5) plus dwie kropki, natomiast 13 to dwie kreski (czyli 10), a nad nimi trzy kropki.
Tajemnice Kodeksu Drezdeńskiego
Jak już wiemy, Majowie byli cywilizacją astronomów. Obserwując niebo gołym okiem, byli w stanie dostrzec nawet subtelne ruchy planet – znane im były Merkury, Wenus, Mars, Jowisz i Saturn. Co ciekawe, architektura ich miast wskazuje na to, że budowle pełniły także rolę obserwatoriów astronomicznych, a przynajmniej ich układ wskazywał na powiązanie z konkretnymi zjawiskami astronomicznymi. Na przykład podczas równonocy wiosennej i jesiennej cienie
4cmna piramidzie El Castillo w Chichén Itzá tworzą wyjątkowy układ. Zdają się wprawiać w ruch umieszczonego na schodach węża, symbolizującego boga Kukulkana związanego z cyklami słonecznymi. Podobny efekt światła i cienia obserwowano także na piramidzie w El Tajina.
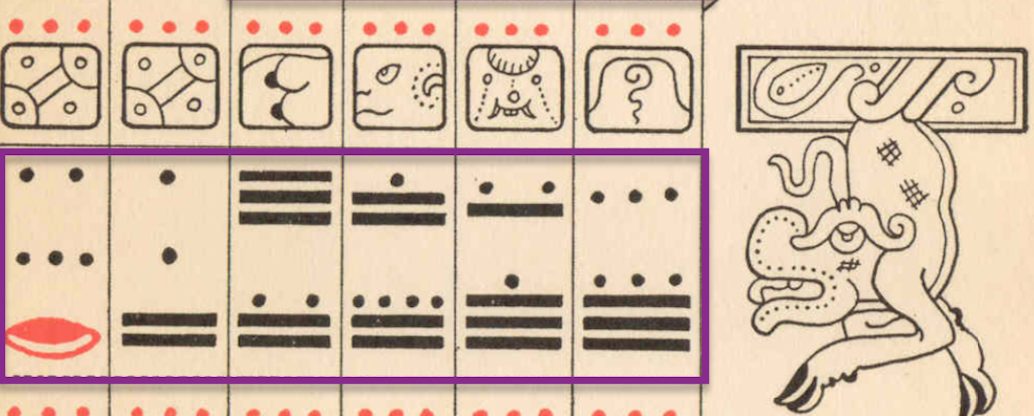
Postać boga Marsa na stronicy Kodeksu Drezdeńskiego
Wszystkie obserwacje astronomiczne Majowie zapisywali w księgach. Jedną z nich jest Kodeks Drezdeński, który zawiera informacje o zjawiskach astronomicznych. Można w nim znaleźć następujący tajemniczy ciąg liczbowy: \(78, 156, 234, 312, 390, 780.\) Jaka jest relacja między tymi liczbami?
Na pierwszy rzut oka widać, że liczby te tworzą ciąg rosnący: \[78 < 156 < 234< 312< 390< 780.\] Aby zgłębić tajemnicę tych liczb, musimy zrozumieć, jaka jest ich wspólna cecha. Zauważmy, że wszystkie one są wielokrotnością 78: \[\begin{aligned} 78 & = 18 + 3 \times 20, \\ 156 & = 16 + 7 \times 20 = 78 \times 2, \\ 234 & = 14 + 11 \times 20 = 78 \times 3, \\ 312 & = 12 + 15 \times 20 = 78 \times 4, \\ 390 & = 10 + 1 \times 20 + 1 \times 18 \times 20 = 78 \times 5, \\ 780 & = 0 + 3 \times 20 + 2 \times 18 \times 20 = 78 \times 10. \end{aligned}\] Ten ciąg jest prawie ciągiem arytmetycznym, czyli takim, w którym różnica między kolejnymi wyrazami jest stała. W ciągu powyżej tylko ostatnia liczba wyłamuje się z tej reguły, ponieważ wynosi \(10 \cdot 78,\) a nie \(6 \cdot 78.\)
Okazuje się jednak, że w innym miejscu w Kodeksie możemy znaleźć brakujące liczby: \[\begin{aligned} 468 & = 78 \times 6, \\ 546 & = 78 \times 7, \\ 624 & = 78 \times 8, \\ 702 & = 78 \times 9. \end{aligned}\]
Dlaczego wielokrotności liczby \(78\) były tak istotne dla Majów? Liczba \(78\) pochodzi od \(780\)-dniowego okresu synodycznego Marsa, czyli czasu, jaki potrzebuje planeta, aby powrócić do tej samej pozycji widzianej z Ziemi. Majowie obliczyli ten okres jako \(780\) dni, podczas gdy rzeczywisty okres synodyczny Marsa wynosi \(779,94\) dnia. Pomiar Majów był więc niezwykle precyzyjny.
Na tej samej stronie Kodeksu Drezdeńskiego, po jej prawej stronie, widzimy zwisającą, dziwną postać. Jest to majański bóg Marsa: bóg burzy, znany również jako „bestia Marsa”, charakteryzujący się ozdobnym nosem. Umieszczenie go na tej stronie Księgi potwierdza, że wszystkie zapisy na tej stronie mają związek z planetą Mars.
Obserwacje Księżyca
Obecnie wiemy, że okres synodyczny Księżyca wynosi średnio 29 dni, 12 godzin, 44 minuty i 3 sekundy. Odstęp między kolejnymi zaćmieniami Księżyca może wynosić 1, 5 lub 6 okresów synodycznych, przy czym \(5\) okresów to mniej więcej \(148\) dni, a \(6\) okresów to nieco ponad \(177\) dni.
Cykle 148 i 177 dni wynikają z geometrii ruchu Księżyca i jego orbity. Księżyc porusza się po orbicie nachylonej o około \(5^{\circ}\) względem płaszczyzny orbity Ziemi (czyli ekliptyki). Dlatego nie wszystkie nowie i pełnie prowadzą do zaćmień – zazwyczaj Księżyc przechodzi powyżej lub poniżej tarczy Słońca (podczas nowiu) lub cienia Ziemi (podczas pełni). Zaćmienia są możliwe tylko wtedy, gdy pozycja Słońca na niebie (z punktu widzenia Ziemi) znajduje się blisko jednego z węzłów orbity Księżyca – miejsc, w których orbita Księżyca przecina płaszczyznę ekliptyki.
Majowie obliczyli, że okres synodyczny Księżyca trwa średnio 29,53 dni. Odkryli także, że wielokrotności tego okresu pokrywają się z tak zwanymi sezonami zaćmień. W szczególności wiedza ta została zapisana w Kodeksie Drezdeńskim. Znajdziemy tam ostrzeżenia przed zaćmieniami, zorganizowane w powtarzających się cyklach 177 dni i 148 dni.
Na potwierdzenie powyższych informacji przyjrzyjmy się teraz kolejnemu rysunkowi.
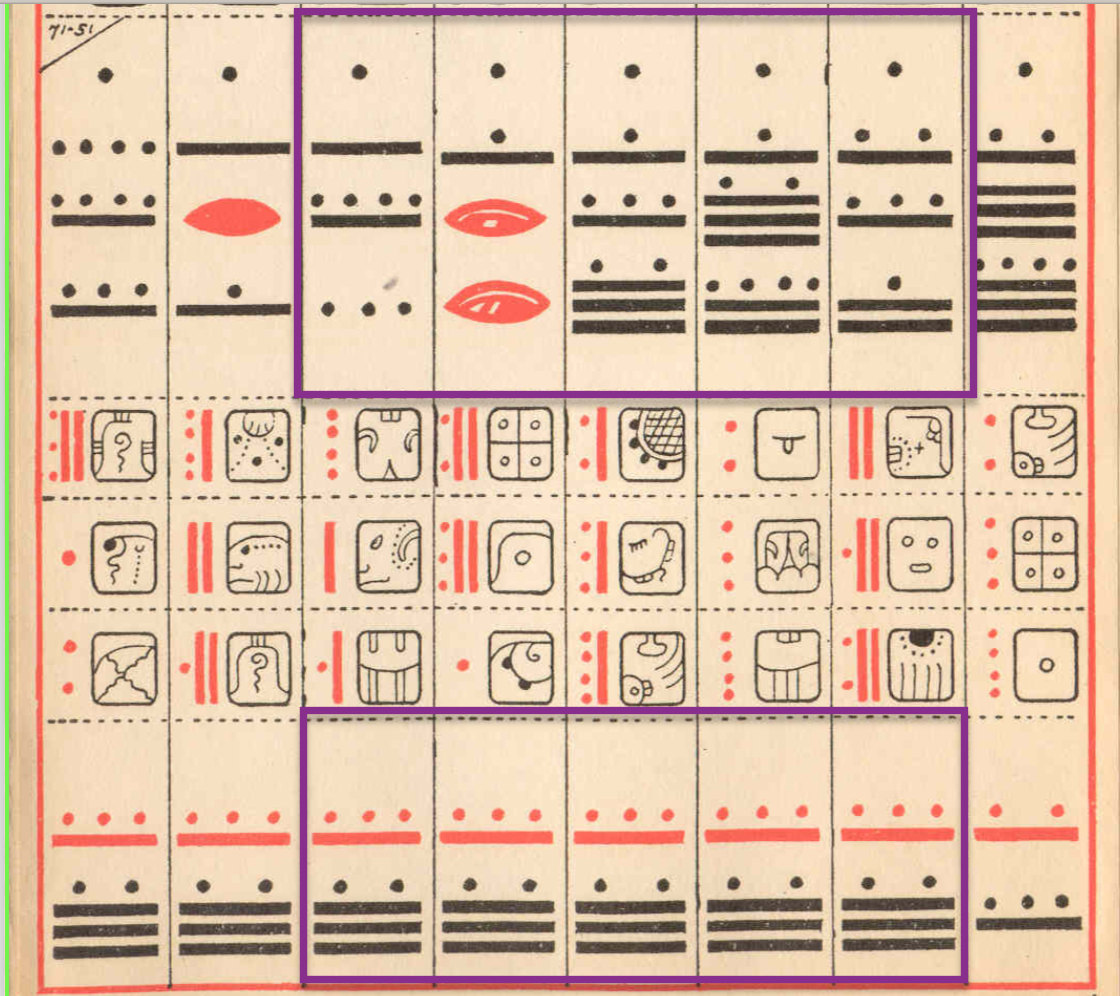
Zwróćmy uwagę na liczby znajdujące się w górnej fioletowej ramce. Liczba po lewej stronie odpowiada 9183 dniom, obliczonym według metody chronologicznej: \[9 183= 3 + 9 \times 20 + 5 \times 18 \times 20 + 1 \times 18 \times 20^2 .\] Druga liczba od lewej to: \[9 360= 0 + 0 \times 20 + 6 \times 18 \times 20 + 1 \times 18 \times 20^2.\]
Podobnie sprawdzamy, że kolejne liczby to: \(9 537\), \(9 714\), \(9 891\) i \(10 039\). Warto zauważyć, że różnica między tymi liczbami (od \(9 183\) do \(9 891\)) wynosi 177, co odpowiada liczbie dni pomiędzy kolejnymi zaćmieniami: \[\begin{aligned} 9 183 + 177 & = 9 360, \\ 9 360 + 177 & = 9 537, \\ 9 537 + 177 & = 9 714, \\ 9 714 + 177 & = 9 891. \\ \end{aligned}\] Potem jednak wzór ulega zmianie, ponieważ \(10 039\) = \(9 891+148\), co oznacza, że w tym przypadku mamy do czynienia z innym cyklem, który trwa 148 dni.
Podsumowanie
Majowie osiągnęli niezwykły poziom zaawansowania matematycznego, który pozwolił im nie tylko opracować własny system liczbowy, ale również – zgodnie ze współczesnym nazewnictwem – arytmetykę modularną. Ich system opierał się głównie na bazie 20, z wyjątkowym przypadkiem użycia bazy \(18 \times 20 = 360\) w kalendarzu długiej rachuby (DK), co świadczy o niespotykanej precyzji w liczeniu czasu.
Używając współczesnej terminologii matematycznej, Majowie wykonywali obliczenia w pierścieniu \((\mathbb{Z}_{20},+,\cdot),\) którego elementy to reszty z dzielenia przez \(20.\) To znaczy, że dodawanie i mnożenie można opisać wzorami: \[\begin{aligned} 2 a\cdot b & \equiv r\mod 20, & & \ \ \ \text{gdzie}\ \ \ r\in \{0,\cdots, 19\}, \\ a + b & \equiv r'\mod 20, & & \ \ \ \text{gdzie}\ \ \ r'\in \{0,\cdots, 19\}. \end{aligned}\] Pierścienie \(\mathbb{Z}_{p},\) gdzie \(p>1\) jest liczbą naturalną, odgrywają ważną rolę we współczesnej matematyce, prowadząc do powstania istotnych struktur algebraicznych, takich jak grupy, pierścienie i ciała.
Majowie intuicyjnie posługiwali się strukturami modularnymi z dużą biegłością, co wyprzedzało ich czasy i stawia ich osiągnięcia matematyczne na wyjątkowym miejscu w historii ludzkości.





