Zadania z matematyki nr 909, 910
Redaguje Marcin E. KUCZMA
909. Trójkąt prostokątny \(ABC\) ma boki \({AB=5a},\) \({BC=4a},\) \({CA=3a}\) (\({a={}}\)jednostka długości). Na boku \(BC\) leżą takie punkty \(D,\) \(E,\) że okręgi o średnicach \(CD\) i \(DE\) są styczne do boku \(AB\) odpowiednio w punktach \(P\) i \(Q.\) Przez dowolnie wybrany punkt \(X\) na odcinku \(AP\) prowadzimy prostą (różną od \(AP\)) styczną do okręgu \(CPD.\) Równoległa do niej prosta styczna do okręgu \(DQE\) przecina półprostą \(QB^\to\) w punkcie \(Y.\) Wyznaczyć minimalną długość odcinka \(XY,\) gdy punkt \(X\) zmienia swoje położenie na odcinku \(AP.\)
910. Rozważamy graf skierowany o nieskończenie wielu wierzchołkach ponumerowanych wszystkimi liczbami całkowitymi nieujemnymi. Krawędź zorientowana od wierzchołka \(\ell\) do wierzchołka \(m\) prowadzi wtedy i tylko wtedy, gdy \({0<m-\ell\le3}\) oraz dokładnie jedna z liczb \(m{-}\ell,\) \(m\ell\) jest podzielna przez 3. Dla każdej liczby naturalnej \(n\) obliczyć, ile jest ścieżek prowadzących od wierzchołka 0 do wierzchołka \(3n.\)
Zadanie 910 zaproponował pan Paweł Kubit z Krakowa.
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
899 (\(WT = 1{,}36\)) i 900 (\(WT = 1{,}56\))
z numeru 4/2025
Marcin Kasperski Warszawa 46,36 Szymon Kitowski 41,11 Krzysztof Maziarz Londyn 40,97 Andrzej Daniluk Warszawa 40,76 Jerzy Cisło Wrocław 40,19 Krzysztof Kamiński Pabianice 38,09 Barbara Mroczek 37,01 Mikołaj Znamierowski 36,54 Roksana Słowik 35,92 Marian Łupieżowiec Gliwice 35,90 Michał Adamaszek Kopenhaga 31,26 Stanisław Bednarek Łódź 31,20 Pan Marcin Kasperski – już podwójny Weteran – sześć pełnych rund!
Zadania z fizyki nr 806, 807
Redaguje Elżbieta ZAWISTOWSKA
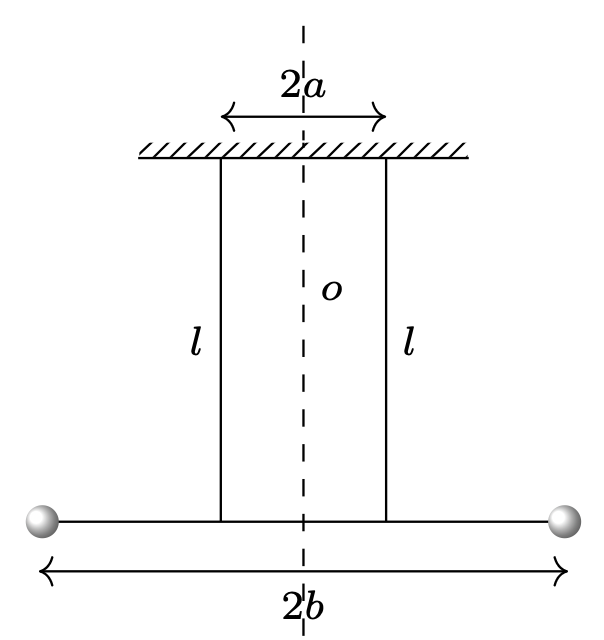
806.Hantla składa się z dwóch jednakowych małych kulek o masach \(m\), zaczepionych na końcach lekkiego pręta i jest zawieszona w położeniu poziomym na dwóch nierozciągliwych niciach o długości \(l\), oddalonych od siebie o \(2a\) (rys. 1). Odległość między kulkami wynosi \(2b\). Znaleźć okres małych drgań skrętnych tej hantli.
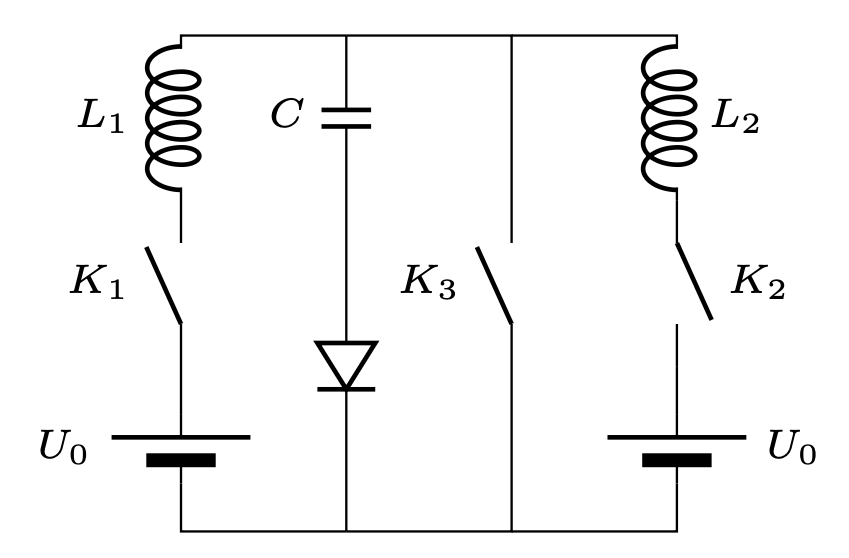
807. W obwodzie przedstawionym na rysunku 2 klucz \(K_{3}\) jest na początku zamknięty, a klucze \(K_{1}\) i \(K_{2}\) otwarte. W pewnej chwili zamknięto klucz \(K_{1}\), a po czasie \(t_{1} = 0{,}1\) s zamknięto klucz \(K_{2}\). Po kolejnym czasie \(t_{2} = 0{,}2\) s otwarto klucz \(K_{3}\). Znaleźć: 1) natężenie prądu przez cewkę \(L_{1}\) po długim czasie od zamknięciu klucza \(K_{1}\); 2) maksymalne napięcie na kondensatorze. Opory omowe zaniedbujemy, dioda jest idealna. Przyjmujemy \(L_{1} = 1\) H, \(L_{2} = 0{,}5\) H, \(C = 10\,\mu\mathrm{F}\), \({U}_{0} = 10\) V.
Rys. 1
Rys. 2
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
796 (\(WT=1{,}75\)), 797 (\(WT=2{,}09\))
z numeru 4/2025
Jacek Konieczny Poznań 41,11 Jan Zambrzycki Białystok 4 – 37,38 Ryszard Woźniak Kraków 34,00 Andrzej Nowogrodzki Chocianów 3 – 32,28 Paweł Perkowski Ożarów Maz. 6 – 21,47 Tomasz Wietecha Tarnów 18 – 18,27 Krzysztof Zygan Lubin 18,16 Paweł Kubit Kraków 17,81 Termin nadsyłania rozwiązań: 31 I 2026