Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Artykuł ten poświęcam pamięci profesora Tadeusza Nadziei, bliskiego kolegi, fascynata historii matematyki.
Twierdzeniem, od którego zaczynają się Principia, jest następujący fundamentalny rezultat.
Teza I. Twierdzenie I. Księga I (prawo pól). Powierzchnie zakreślane przez pociągnięte do nieruchomych centrów sił promienie wodzące krążących ciał leżą we wspólnych płaszczyznach i są proporcjonalne do czasów, w których są zakreślane. [Newton, 2015]
Isaac Newton, Matematyczne Zasady Filozofii Naturalnej, Copernicus Center Press, 2015
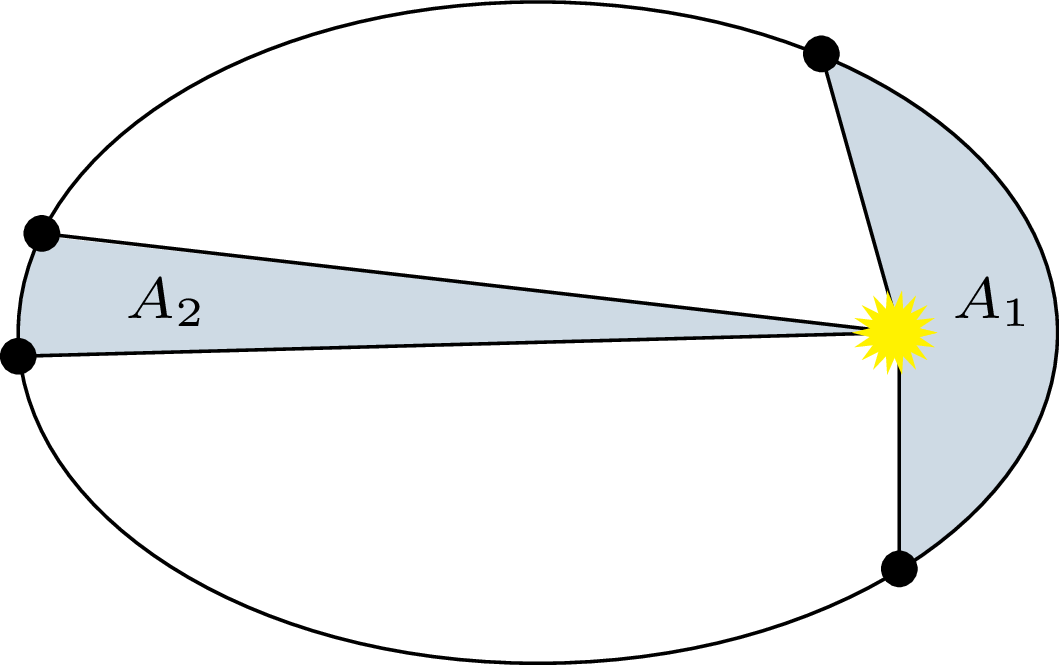
Chodzi tu o centralne pole sił, a więc układ, w którym siła działająca na ciało \(P\) jest proporcjonalna do wektora \(\overrightarrow{OP}\) (wektora wodzącego), gdzie \(O\) jest ustalonym punktem (centrum siły). Wówczas w równych odstępach czasu wektor wodzący zakreśla figury o równym polu. Możemy rozsądnie przyjąć, że Newtonowi chodziło o dowolne ciągłe pola sił i gładkie orbity. Celem Principiów było bowiem badanie realnego świata fizycznego, w szczególności Układu Słonecznego, a nie budowanie abstrakcyjnej teorii matematycznej. Przykładem opisanej tu sytuacji jest drugie prawo Keplera, w którym centrum siły jest umieszczone w nieruchomym Słońcu, a ciałami przyciąganymi przez nie są planety poruszające się po orbitach eliptycznych (rys. 1).
Rys. 1. Drugie prawo Keplera to szczególny przypadek prawa pól
Michael Nauenberg w [Nauenberg, 2003] napisał, że ,,Słusznie uważa się tę tezę za kamień węgielny Principiów, ponieważ proporcjonalność między obszarem omiatanym przez wektor promienia orbity a upływającym czasem umożliwiła Newtonowi rozwiązywanie problemów dynamicznych metodami czysto geometrycznymi, uzupełnionymi przez argumenty ciągłego przejścia do granicy, które sam rozwinął”.
Odnotujmy, że Twierdzenie mówi o dwóch własnościach ruchu:
Własność 1. ruch odbywa się w nieruchomej płaszczyźnie;
Własność 2. pola powierzchni zakreślonych przez promień wodzący są proporcjonalne do czasów, w których są zakreślone.
Analityczny dowód prawa pól
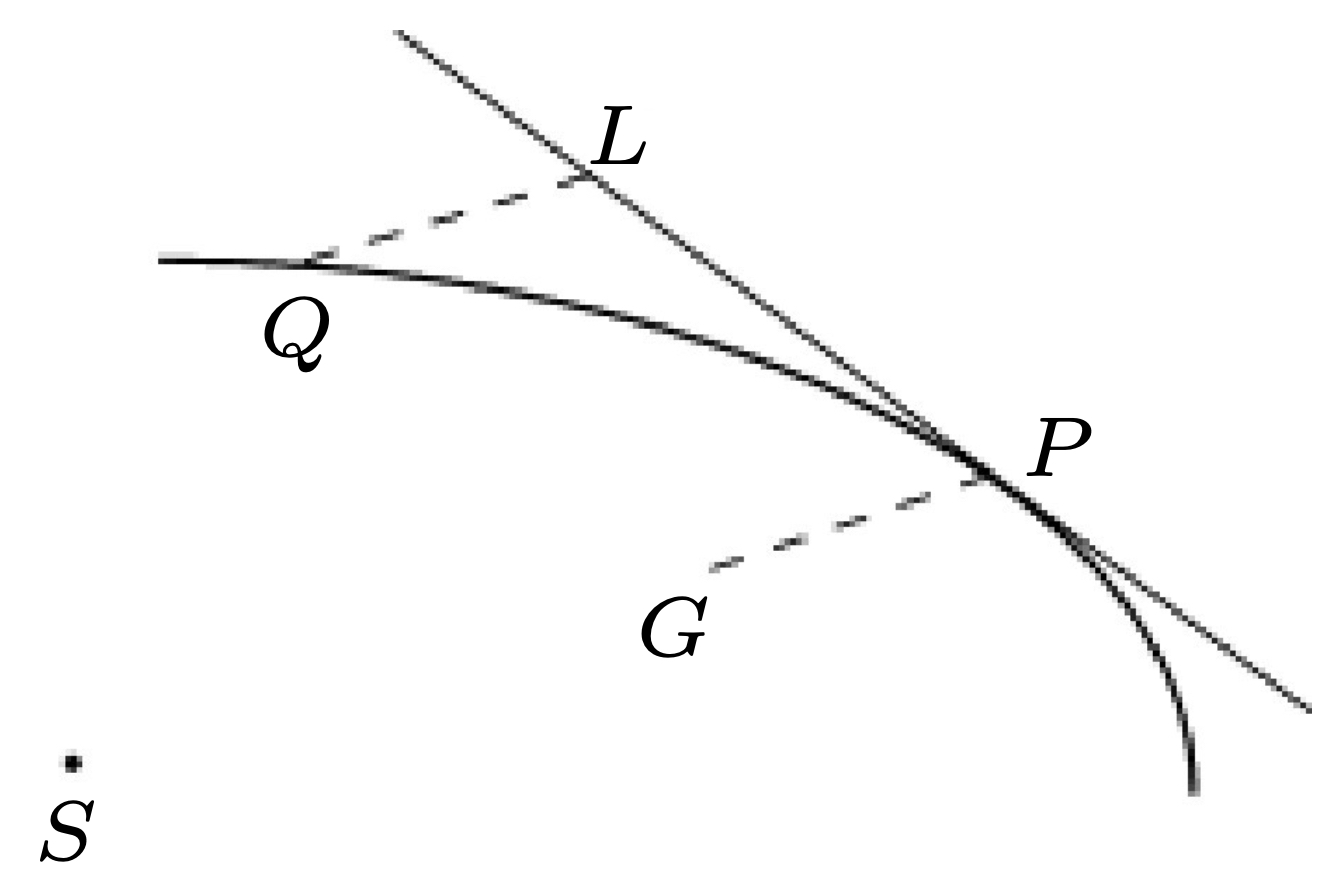
Rys. 2. Ruch po trajektorii \(PQ\) to odchylenie ruchu bezwładnego w kierunku \(PL\) spowodowane ciągłą siłą działającą w kierunku centrum \(S.\) Po pewnej chwili \(h\) ciało znajduje się w punkcie \(Q\) (zamiast w punkcie \(L\)). Miarą tej siły w punkcie \(P\) jest granica \(\lim_{h\to 0}(\vec{LQ}/h^2).\)
Odchylenie wzdłuż przekątnej \(PQ\) równoległoboku \(PGQL\) odpowiadałoby hipotetycznej sile impulsowej w punkcie \(P,\) dla której powyższa granica jest nieskończona.
Współczesny dowód Twierdzenia I, standardowo przytaczany w podręcznikach fizyki, opiera się na pokazaniu, że wektor momentu pędu \(\vec{L}= \vec{r}\times \vec{p}\) ciała o masie \(m\) poruszającego się w centralnym polu sił \(\vec{f}\) nie zmienia się w czasie; jest to równoważne tezie Twierdzenia I.
Dowód jest następujący. Różniczkując \(\vec{L}\) względem czasu, otrzymujemy: \[\frac{d \vec{L}}{dt} = \frac{d \vec{r}}{dt} \times \vec{p}+ \vec{r}\times \frac{d\vec{p}}{dt} = 0,\] gdyż \(\frac{d\vec{r}}{dt} = \vec{v} = \frac{\vec{p}}{m}\) oraz \(\frac{d\vec{p}}{dt} = \vec{f},\) a iloczyn wektorowy wektorów współliniowych jest równy zeru. To oznacza, że wektor \(\vec{L}\) jest niezmienny w czasie. Stałość jego zwrotu dowodzi własności 1, a stałość jego długości – własności 2.
Trudności interpretacyjne Principiów
Wobec nieostrości określeń w Twierdzeniu I, w jego dowodzie przedstawionym poniżej, a także w całych Principiach, Czytelnikowi należą się pewne wyjaśnienia. Otóż w swoim opus magnum Newton określa podstawowe pojęcia nie zawsze w tych miejscach, w których powinny być precyzyjnie zdefiniowane, według naszych standardów. Robi to jakby przy okazji, przeważnie tam, gdzie ich używa w subtelniejszych dowodach. Nierzadko trzeba rozszyfrowywać, jakie znaczenie danego określenia miał na myśli. Na przykład komentatorzy nie są zgodni, czy w podstawowym dla całej teorii drugim prawie ruchu siła jest impulsowa, czy ciągła [Pourciau, 2016]. Należy się wielu rzeczy doszukiwać z kontekstów rozrzuconych po całych Principiach. Dotyczy to też pojęcia siły użytego w powyższym twierdzeniu. Stąd właśnie, paradoksalnie, Principia są dziełem aktualnym, żywym i inspirującym, dziełem otwartym. Inspirują one każdą kolejną generację w nieco odmienny sposób, właśnie dzięki obecnym w nich możliwościach interpretacyjnych, ,,dziurach” czy pozornych sprzecznościach, oczywiście w połączeniu z rewolucyjnym charakterem samego dzieła. Notabene opisane wyżej własności Principiów, przełomowego dzieła naukowego, są wspólne także dla wielu najwybitniejszych dzieł religii, filozofii i literatury.
Na potwierdzenie faktu, że deszyfracja, bo tak trzeba nazwać odczytywanie Principiów, jest bardzo trudna nawet dla znawców przedmiotu, podajemy dwa konkretne przykłady. W artykule [Nauenberg, 1994] przedstawione są (wraz z obszernym komentarzem) dwie różne opinie dotyczące kwestii podstawowej: czy w Principiach znajduje się dowód, że prawo grawitacji Newtona implikuje orbity stożkowe? Natomiast w artykule autora z \(\Delta^{10}_{20}\) zarysowana jest historia słynnego Lematu XXVIII w Principiach, dotyczącego niewspółmierności pola wycinka owalu i opisującej ten wycinek prostej, gdzie trwające ponad trzy stulecia zarzuty wobec jego dowodu znikają dopiero po zrozumieniu, co Newton uważał za owal.
W tym artykule skupimy się głównie na rozważaniach dotyczących Własności 1.
Dowód prawa pól w Principiach
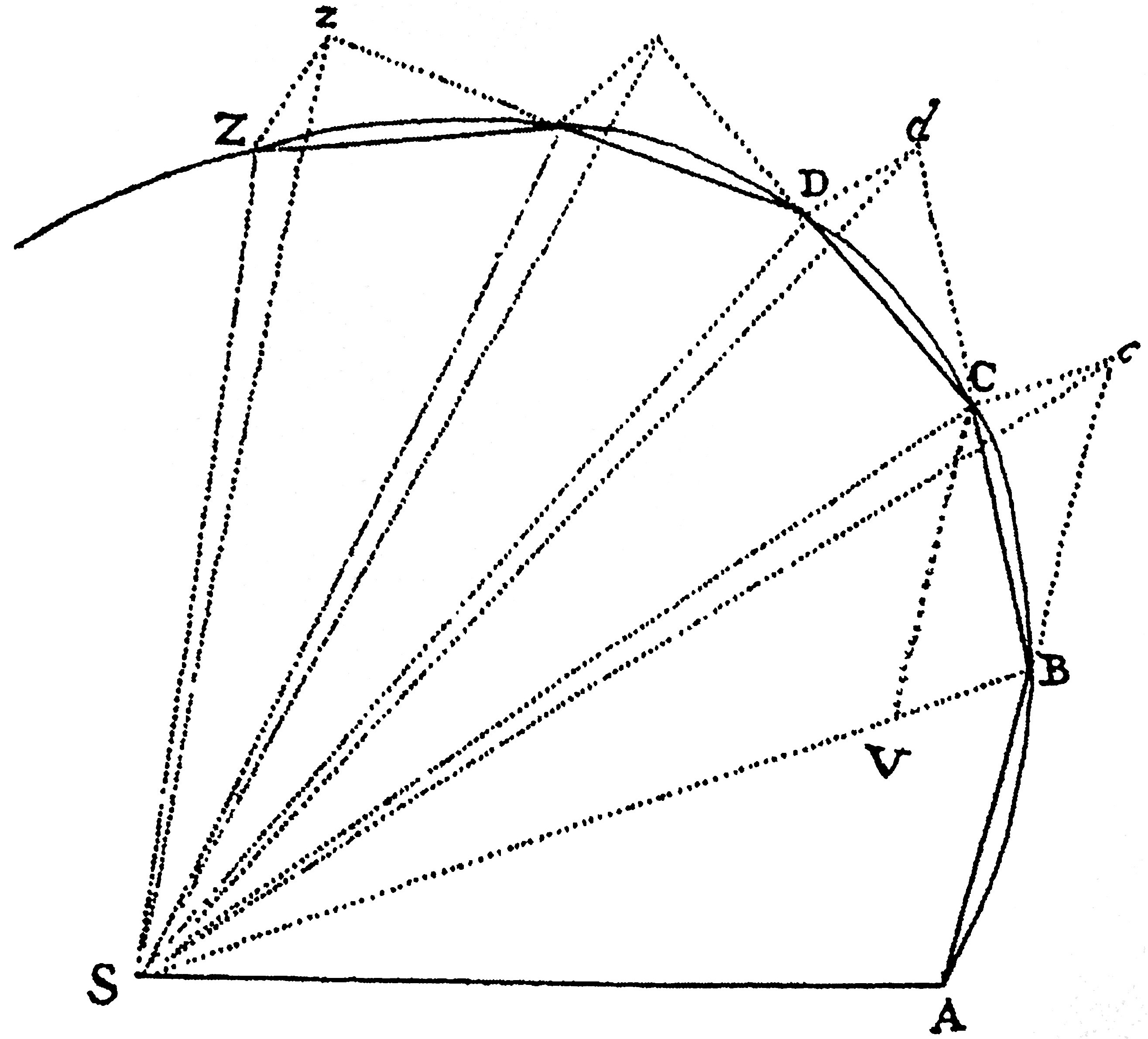
Poniższy dowód Twierdzenia I, przedstawiony przez Newtona w Principiach, jest opatrzony rysunkiem 3.
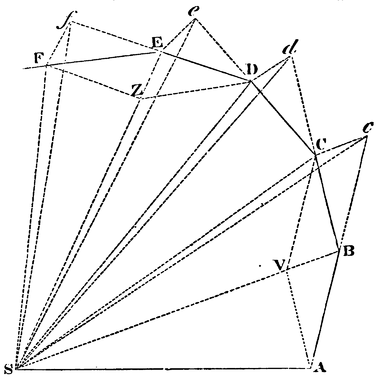
Rys. 3. Aproksymacja orbity
Załóżmy, że czas podzielono na jednakowe części i niech w pierwszej części tego czasu ciało – pod działaniem bezwładności (vis insita) – porusza się po odcinku \(AB.\) W drugiej części tego czasu, przy braku bodźca, ruch zostałby, na podstawie pierwszego prawa Newtona, podobnie przedłużony prosto do \(c\) wzdłuż odcinka \(Bc,\) równego odcinkowi \(AB,\) tak więc promienie \(AS,\) \(BS,\) \(cS,\) pociągnięte do centrum, wyznaczyłyby jednakowe powierzchnie \(ASB\) i \(BSc.\) Załóżmy jednakże, że gdy ciało pojawia się w \(B,\) działa na nie nagle mocny impuls siły dośrodkowej, który odchylając ciało z prostej linii \(Bc,\) zmusza je do kontynuowania ruchu wzdłuż prostej linii \(BC.\) Narysujmy odcinek \(cC\) równoległy do \(BS\) i przecinający się z \(BC\) w punkcie \(C.\) [Na mocy Wniosku 1 z Praw], na końcu drugiej części czasu ciało znajdzie się w \(C,\) we wspólnej płaszczyźnie z trójkątem \(ASB.\) Połączmy \(S\) i \(C\) i zauważmy, że skoro \(SB\) i \(Cc\) są równoległe, to powierzchnia trójkąta \(SBC\) będzie równa powierzchni trójkąta \(SBc\) i stąd równa też powierzchni trójkąta \(SAB.\) Z podobnych przyczyn, jeżeli siła dośrodkowa działa kolejno w punktach \(C,\) \(D,\) \(E\) itd. i zmusza ciało w każdej pojedynczej chwili czasu do zakreślania prostych odcinków \(CD,\) \(DE,\) \(EF\) itd., wszystkie one będą leżały w tej samej płaszczyźnie, a powierzchnia trójkąta \(SCD\) będzie równa powierzchni trójkąta \(SBC,\) powierzchnia \(SDE\) równa powierzchni \(SCD,\) powierzchnia \(SEF\) równa powierzchni \(SDE.\) I dlatego w jednakowych czasach są zakreślane jednakowe powierzchnie leżące w jednej nieruchomej płaszczyźnie i – na zasadzie łączenia – wszelkie sumy tych powierzchni, takie jak \(SADS,\) \(SAFS,\) mają się do siebie tak, jak czasy, w których są zakreślane. Niech teraz liczba tych trójkątów będzie zwiększona, a ich szerokość zmniejszona in infinitum. [Na podstawie Wniosku 4 z Lematu III] ich ostateczna zewnętrzna granica \(ADF\) będzie linią krzywą i dlatego siła dośrodkowa, przez którą ciało jest ustawicznie odciągane od stycznej do tej krzywej, będzie działała w sposób ciągły, a każda z zakreślonych powierzchni \(SADS,\) \(SAFS,\) które są zawsze proporcjonalne do czasów zakreślania, będzie – również w tym przypadku – proporcjonalna do tych czasów. Q.E.D. [Newton, 2015].
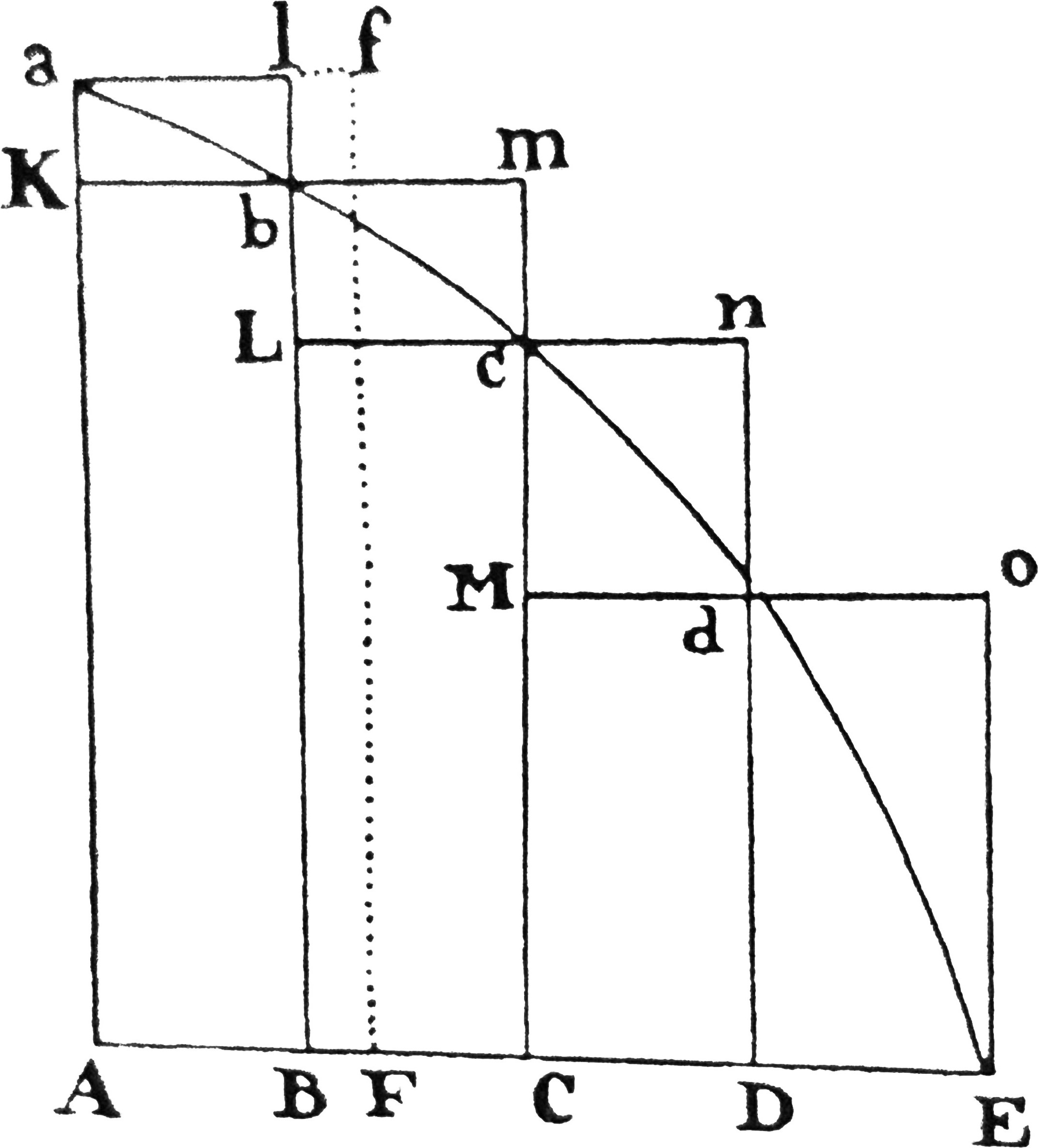
Rys. 4. Rysunek do Lematu III, Księgi I, pokazujący aproksymację pola pod ciągłą krzywą przez sumę pól prostokątów w nią wpisanych i na niej opisanych. W Lemacie III Newton dowodzi, że gdy podstawy tych prostokątów są coraz mniejsze, to obie sumy dążą (z dołu i z góry, odpowiednio) do pola pod krzywą \(a,c,E.\)
Rys. 5. Orbita i jej aproksymacja
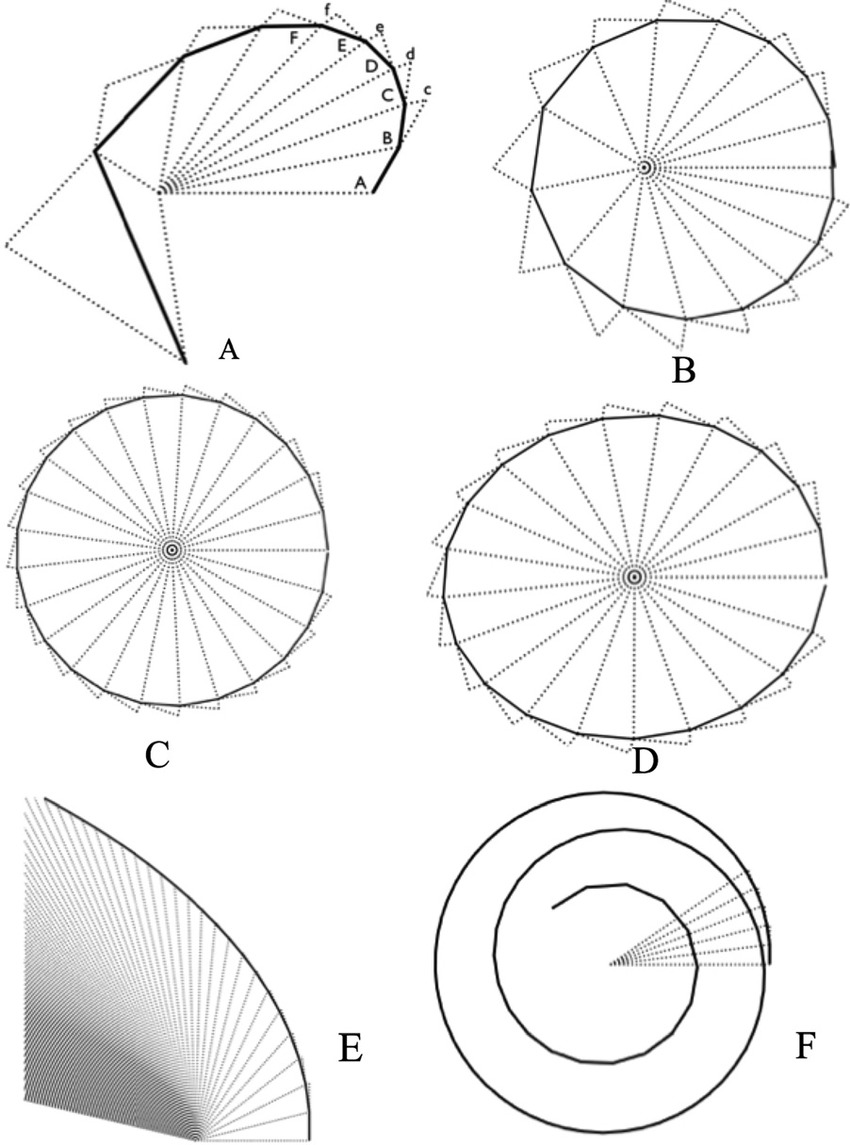
Rys. 6. Aproksymacje orbit w polu siły centralnej proporcjonalnej.
(1) do \(\frac{1}{r^2}\): (A) – diagram z De Motu Newtona rozszerzony o 4 dodatkowe impulsy, (B),(E) – orbity eliptyczna i hiperboliczna z centrum siły w ich ogniskach,
(2) do \(\frac{1}{r^3}\): (F) – orbita spiralna (\(\ln r = a \theta\)),
(3) do \(r\): (C) – orbita kołowa z centrum siły w środku okręgu, (D) – orbita eliptyczna z centrum siły w środku elipsy. [Nauenberg, 2018]
Od czasu publikacji Principiów dowód ten był i nadal jest komentowany, krytykowany lub broniony przez kolejnych autorów. Pierwsze zarzuty, jakie sformułowano wobec dowodu Twierdzenia I – poczynając od samego Edmonda Halleya, promotora Principiów – dotyczyły argumentu przejścia do granicy w jego końcowym fragmencie, rozpoczynającym się od słów Niech teraz liczba tych trójkątów będzie zwiększona, a ich szerokość zmniejszona in infinitum. Rzeczywiście, argumentacja Newtona jest tu dość enigmatyczna. Pewne uzupełnienie tego fragmentu dowodu zaproponowane jest w [Nauenberg, 2003].
Zastrzeżenia wobec dowodu Własności 1
Całkiem niedawno Bruce Pourciau [Pourciau, 2016] stwierdził, że w dowodzie jest luka natury logicznej i dotyczy własności ,,ruch odbywa się w nieruchomej płaszczyźnie”. Natomiast po przesunięciu tej własności z tezy do założeń Twierdzenia I dowód Newtona można już przedstawić precyzyjnie, dokonując niewielkich zmian i uzupełnień. Taka modyfikacja prawa pól oczywiście je osłabia. Gdybyśmy mogli poprosić Sir Isaaca o uzupełnienie jego własnego dowodu, może by nam pomógł, gdyż luka wygląda na istotną.
Zauważmy bowiem, że nawet gdybyśmy nie wyrażali ewentualnych zastrzeżeń wobec argumentu przejścia do granicy, to na podstawie odniesienia do Wniosku 4 z Lematu III w dowodzie Twierdzenia 1 oraz samego Lematu III opatrzonego rysunkiem 4 możemy wnioskować, iż Newton milcząco założył, że wielokąt \(A,\)\(B,\)\(C,\)\(D,\)\(E,\)\(F,\) … jest wpisany w ciągłą orbitę poruszającego się ciała. W takim razie sama orbita jest płaska, ale to właśnie należy pokazać. Konstrukcja Newtona dotyczyłaby zatem tylko orbit płaskich dających się aproksymować, w sensie pola, wielokątami w nie wpisanymi.
Czy Newton mógłby popełnić tak elementarny błąd? Wydaje się to mało prawdopodobne.
Szkic dowodu prawa pól w wersji osłabionej
Jak można doprecyzować powyższy dowód prawa pól przy założeniu, że orbity leżą w nieruchomych płaszczyznach? Pourciau zaproponował odpowiednie przeformułowanie dowodu [Pourciau, 2016], które tutaj zarysujemy.
Należy zacząć od orbity. Niech pierwsze ciało porusza się w polu centralnym wokół punktu \(S,\) po płaskiej orbicie. Załóżmy, że w czasie od \(0\) do \(\Delta t\) pokonuje ono łuk \(AB\) (patrz rys. 5). Przyjmijmy teraz, że drugie ciało, identyczne z pierwszym, pokonuje w tym samym czasie drogę z \(A\) do \(B\) ruchem jednostajnym po odcinku. Gdyby pozostało bezwładne, w odstępie \(\Delta t\) pokonałoby odcinek \(Bc\) takiej samej długości. Załóżmy jednak, że w chwili \(\Delta t\) działa na nie impuls siły dośrodkowej, zmieniając jego prędkość o wektor równoległy do \(SB\) w taki sposób, że odcinek \(BC\) pokonany w odstępie \(\Delta t\) kończy się ponownie na docelowej orbicie. Równość pól trójkątów \(SAB,\) \(SBc,\) \(SBC\) wynika wtedy z przystawania \(AB \equiv Bc\) i równoległości \(cC \parallel SB.\) Podobnie każdy kolejny trójkąt zakreślony w odstępie \(\Delta t\) ma to samo pole.
Oczywiście i w tym przypadku konieczny jest odpowiedni argument przy przejściu do granicy \(\Delta t \to 0.\) Obszerne rozważania dotyczące tego punktu można znaleźć w [Pourciau, 2016], patrz także [Nauenberg, 2003, 2018].
Domysły dotyczące brakującej części dowodu Twierdzenia I
Wobec naszego przekonania, że Newton nie mógł popełnić opisanego wyżej elementarnego błędu logicznego, oraz wobec prostoty argumentów dowodu analitycznego narzuca się wręcz konstatacja, że być może brakująca część dowodu Twierdzenia I znalazła się w manuskrypcie Principiów, lecz Newton wykreślił stosowne uzasadnienia w momencie przekazywania dzieła do druku, uznawszy je ostatecznie za łatwe do uzupełnienia przez czytelników pokroju Huygensa i Leibniza. Należy tu zaznaczyć, że koszty druku tak obszernego dzieła były wysokie. Pokrył je osobiście Edmond Halley, gdyż Towarzystwo Królewskie było spłukane i mogło dać tylko swoje imprimatur, udzielone latem 1886 roku przez przewodniczącego Samuela Pepysa; jego nazwisko znajduje się dzięki temu na karcie tytułowej (rys. 7). To jednak tylko domysły, bowiem kluczowe arkusze manuskryptu Principiów nie zostały odnalezione. Należy też wziąć pod uwagę fakt, że w Principiach Newton stosował politykę ukrywania dowodów analitycznych stojących za konstrukcjami geometrycznymi. Koronnym przykładem jest jego dowód Wniosku III do Tezy XLI Zadania XXVIII.
Rys. 7. Strona tytułowa pierwszego wydania Principiów, Londyn 1687
Teza XLI. Zadanie XXVIII. Zakładając siłę dośrodkową dowolnego rodzaju i przyjmując kwadratury figur krzywoliniowych, należy znaleźć zarówno krzywe, po których ciała będą się poruszać, jak i czasy ich ruchów po tak znalezionych krzywych [Newton, 2015].
Ogólne relacje dotyczące krzywych i czasów, które otrzymał Newton, są równoważne reprezentacjom całkowym z współczesnych podręczników. Uwaga o kwadraturach dotyczy możliwości obliczenia całek. Po podstawieniu pod całkę danych dla newtonowskiego pola grawitacyjnego otrzymujemy krzywe stożkowe. We Wniosku III do tego twierdzenia Newton opisał też – w syntetycznej, geometrycznej formie – krzywe dla siły proporcjonalnej do odwrotności sześcianu odległości od centrum. Wymagało to obliczenia trudnych całek, których jednakże Newton nie uznał za stosowne przytoczyć. Zakończył za to swój dowód uwagą, która mogła sfrustrować każdego czytelnika.
,,Wszystko to wynika z poprzedniej Tezy XLI na drodze kwadratury odpowiedniej krzywej, opis wyznaczania której, jako dostatecznie łatwy, dla zwięzłości opuszczę”. [Pask, 2013]
Rys. 8. Część listu Newtona napisanego do Davida Gregory’ego w 1694 r., wyjaśniającego, jak postępować w przypadku odwrotnego sześcianu użytego we Wniosku III
Collin Pask dodaje: Nic dziwnego, że Newtonowi udało się zdenerwować tak wielu ludzi! Jedną z osób, które poprosiły Newtona o pomoc, był David Gregory, i w 1694 roku Newton napisał do niego, wyjaśniając, jak to działa. O dziwo, list przetrwał i widać (rys. 8), że Newton używa do przeprowadzania całkowania formy rachunku różniczkowego, która jest nam dzisiaj dobrze znana.
Bibliografia
G. Łukaszewicz, M. Sierżęga, Drugie prawo Keplera i owale Newtona. Kontrowersje wokół Lematu XXVIII w Principiach, Delta 10, 2020.
M. Nauenberg, Newton’s Principia and Inverse-Square Orbits, The College Mathematical Journal, vol. 25, 1994, 212–222.
M. Nauenberg, Kepler’s Area Law in the Principia: Filling in some details in Newton’s proof of Proposition 1, Historia Mathematica, Vol. 30, Issue 4, November 2003, 441–456.
M. Nauenberg, Newton’s graphical method for central force orbits, Am. J. Phys., Vol. 86, No. 10, October 2018.
Isaac Newton, Matematyczne zasady filozofii naturalnej, Copernicus Center Press, 2015.
Colin Pask, Magnificent Principia, Prometheus Books, 2013.
B. Pourciau, Instantaneous impulse and continuous force: the foundations of Newton’s Principia, 93–186, in The Cambridge Companion to Newton, wyd. 2, 2016.