Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Rozstania są ciężkie. Czasem trzeba podzielić się wspólnymi książkami, czasem wspólnym psem. Najgorzej jest jednak, gdy mamy wspólną szachownicę. Jeżeli nie dojdziemy do porozumienia, to możemy skończyć z połową szachownicy. A jak negocjacje pójdą bardzo źle, to z połową trójkątną, na której nie możemy nawet poćwiczyć debiutów.
Dla takiej dziwnej półszachownicy zastanowimy się nad klasycznym problemem: na ile sposobów możemy rozstawić kilka, powiedzmy 4, nieatakujące się wieże? Wieże atakują się, kiedy są w tym samym wierszu lub w tej samej kolumnie.
Jeżeli uczyliśmy się kiedyś programować, to aby odpowiedzieć na to pytanie, możemy napisać prosty program, który rozważy wszystkie możliwe rozstawienia wież i dla każdego sprawdzi, czy jest poprawne. Jeśli jest – dodajemy do naszego licznika jeden. Poniżej znajduje się pseudokod takiego programu (w którym, o dziwo, wcięcia tworzą półszachownicę).
Kolejne pętle algorytmu odpowiadają kolejnym wierszom półszachownicy. Wartością \(0\) oznaczamy fakt, że w danym wierszu nie postawiliśmy wieży.
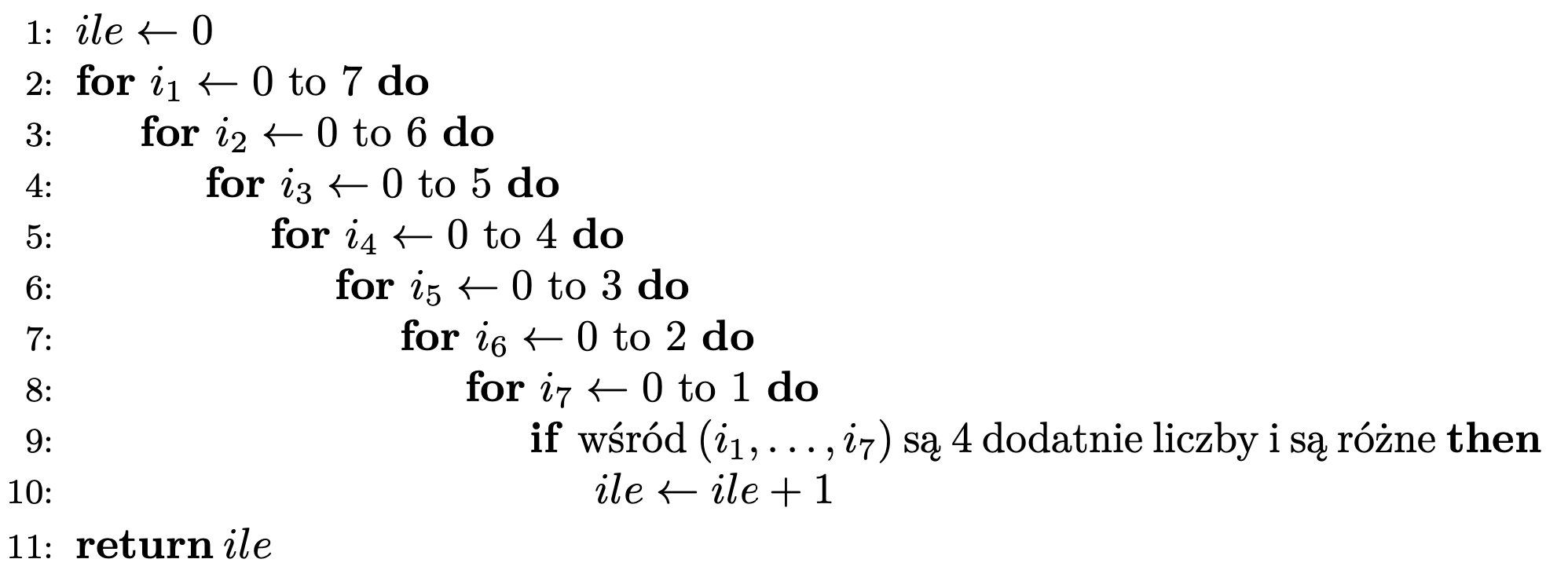 Ten algorytm działa i wyznaczył liczbę 1701. Czuję jednak, że Bardziej Doświadczeni Czytelnicy, widząc go, mogli złapać się za głowę.
Nasze rozwiązanie nie jest bowiem idealne (łagodnie mówiąc). Widzimy na przykład, że gdybyśmy mieli planszę o 20 wierszach, musielibyśmy napisać nowy program, który miałby 20 pętli. Czy da się tego uniknąć? Oczywiście, że tak – wystarczy użyć rekurencji.
Ten algorytm działa i wyznaczył liczbę 1701. Czuję jednak, że Bardziej Doświadczeni Czytelnicy, widząc go, mogli złapać się za głowę.
Nasze rozwiązanie nie jest bowiem idealne (łagodnie mówiąc). Widzimy na przykład, że gdybyśmy mieli planszę o 20 wierszach, musielibyśmy napisać nowy program, który miałby 20 pętli. Czy da się tego uniknąć? Oczywiście, że tak – wystarczy użyć rekurencji.
Napiszmy funkcję, która – wiedząc, ile wierszy (\(n\)) i wież (\(k\)) zostało jeszcze do rozpatrzenia oraz które kolumny są już zajęte (\(kolumny[i] \in \{0,1\}\) to liczba wież w \(i\)-tej kolumnie) – policzy, ile jest rozmieszczeń wież. Funkcja ta będzie wywoływała siebie samą dla mniejszej liczby wierszy. Nie jest to problemem, musimy tylko zadbać o warunki brzegowe, aby obliczenie się zakończyło.
Jeżeli mamy więcej wież niż wierszy, to nam się nie uda – zwracamy \(0\) (linia 2). Jeżeli postawiliśmy już wszystkie wieże, to zwracamy \(1\) (linia 3). Jeżeli żaden z tych warunków nie zachodzi, to jest co najmniej jedna wieża do postawienia, a wierszy co najmniej tyle co wież. Najpierw rozpatrujemy niepostawienie wieży w ostatnim wierszu (linia 4), a następnie postawienie jej kolejno w kolumnach \(1,2,\dots,n,\) jeżeli są puste (linie 5–9).
 Ten algorytm też działa i też wyszło mu 1701. Zaczynamy podejrzewać, że jest to zatem dobry wynik.
A jak szybkie są nasze algorytmy, czyli jaka jest ich złożoność? Koszmarna! \(O(n!)\)!
Zamiast programować, musimy chyba jednak pomyśleć.
Ten algorytm też działa i też wyszło mu 1701. Zaczynamy podejrzewać, że jest to zatem dobry wynik.
A jak szybkie są nasze algorytmy, czyli jaka jest ich złożoność? Koszmarna! \(O(n!)\)!
Zamiast programować, musimy chyba jednak pomyśleć.
Oznacza to z grubsza, że liczba kroków, jakie algorytmy wykonują, może być rzędu \(n!.\)
Oba powyższe algorytmy w trakcie działania przeglądają wszystkie możliwe rozstawienia wież. Nie musimy jednak tego robić – zależy nam przecież tylko na ich liczbie. Niech \(A(n,k)\) będzie szukaną liczbą rozstawień \(k\) wież na półszachownicy o \(n\) wierszach. Zastanówmy się, jak, znając liczbę rozstawień dowolnej liczby wież dla mniejszej półszachownicy, wyznaczyć \(A(n,k).\) W rozstawieniach tych albo w ostatnim wierszu jest wieża, albo nie. Rozstawień bez wieży jest dokładnie tyle samo co rozstawień \(k\) wież na planszy bez ostatniego wiersza, czyli \(A(n-1,k).\) Rozstawienia z wieżą w ostatnim wierszu to po prostu rozstawienia \(k-1\) wież na planszy bez ostatniego wiersza rozszerzone o dostawienie wieży w ostatnim wierszu. Tę wieżę zawsze możemy dostawić na \(n-(k-1)\) sposobów, bo \((k-1)\) kolumn jest już zajętych. Dostajemy więc następujące równanie rekurencyjne: \[A(n,k) = A(n-1,k) + (n-k+1) A(n-1,k-1) \ \ \ \mbox{ dla }n \ge k>0.\] Dodatkowo musimy przyjąć \(A(n,0) = 1\) oraz \(A(n,k)=0\) dla \(n<k.\) Możemy teraz sformułować algorytm dynamiczny oparty na powyższym równaniu rekurencyjnym, który po prostu wypełnia tabelkę znajdującą się na marginesie.
Okazuje się, że tabelka też jest półszachownicą. Przypadek?
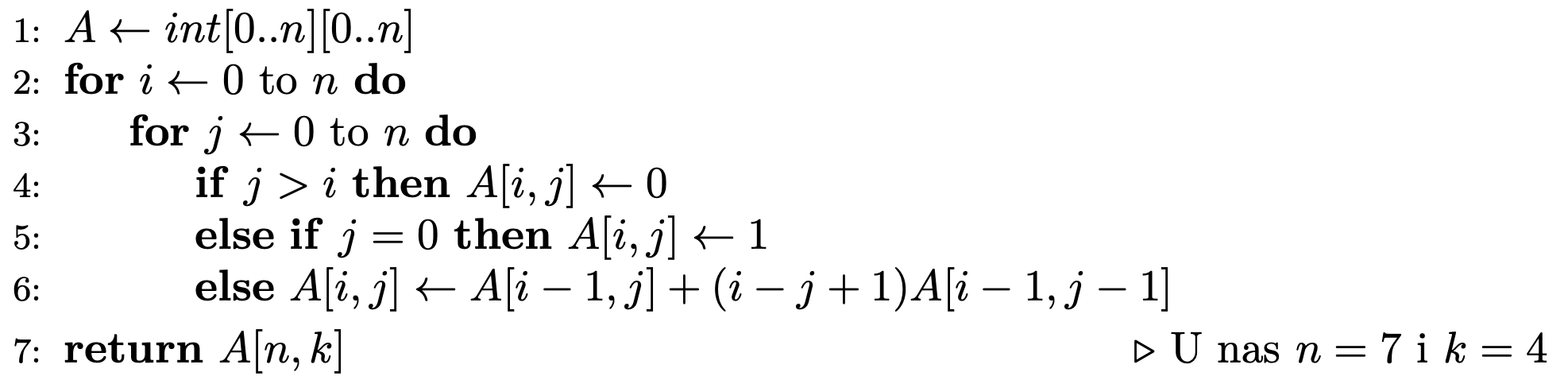
Ten algorytm działa w czasie \(O(n^2).\) No i znowu znaleźliśmy liczbę 1701!
Jeżeli zależało nam tylko na efektywnej metodzie znalezienia wyniku, to może nam to wystarczyć, jednak z naukowej ciekawości fajnie byłoby trochę lepiej zrozumieć, czym są liczby w tej tabelce. Na pierwszy rzut oka nie przypominają niczego szczególnego. Spróbujmy jednak jakoś je wytropić.
W tym celu wpiszmy ciąg złożony z kolejnych wierszy \((1,1,1,1,3,1,1,6,7,\dots)\) w internetową encyklopedię ciągów: oeis.org. Okazuje się, że jest to ,,odbity trójkąt liczb Stirlinga drugiego rodzaju”. Co to znaczy? Liczby Stirlinga drugiego rodzaju opisują liczbę różnych podziałów zbioru na podzbiory. Konkretniej, dla liczb naturalnych \(n,k,\) \(\genfrac{\{}{\}}{0pt}{}{n}{k}\) to liczba możliwych podziałów zbioru złożonego z \(n\) rozróżnialnych elementów na \(k\) podzbiorów. Rzeczywiście, patrząc na trójkąt liczb Stirlinga, widzimy, że wygląda prawie identycznie jak nasz – jest tylko trochę przesunięty (o jeden wiersz i kolumnę w dół) i każdy jego wiersz ma odwróconą kolejność. Dokładniej: \[A(n,k) = \genfrac{\{}{\}}{0pt}{}{n+1}{n+1-k} = \mbox{ liczba podziałów $\{1,\dots,n+1\}$ na $n+1-k$ podzbiorów}.\] Chwila, chwila, zliczaliśmy rozstawienia wież i wyszły nam podziały zbioru? Jakiemu podziałowi ma niby odpowiadać rozstawienie wież z początku artykułu? Jest to co najmniej dziwne. Okazuje się jednak, że istnienie tej odpowiedniości to prawda! I to nie byle jaka, bo to taka prawda, którą można ładnie udowodnić. A takie prawdy to jest to, co w Delcie lubimy najbardziej.
Przykładowo \(\genfrac{\{}{\}}{0pt}{}{4}{2} = 7,\) bo mamy 7 podziałów zbioru \(\{1,2,3,4\}\): \(\{\{1\}, \{2,3,4\}\},\) \(\{\{1,2\}, \{3,4\}\},\) \(\{\{1,3\},\{2,4\}\},\) \(\{\{1,4\},\{2,3\}\},\) \(\{\{1,2,3\},\{4\}\},\) \(\{\{1,2,4\},\{3\}\}\) i w końcu \(\{\{1,3,4\},\{2\}\}.\)
Tak, tak, można też wybrać nudną ścieżkę i pokazać, że liczby Stirlinga spełniają analogiczne równanie rekurencyjne i warunki brzegowe. Ten dowód, chociaż poprawny, ma w sobie tyle polotu co nasz pierwszy algorytm.
Powyższe rozstawienie wież odpowiada podziałowi \(\{1,\dots,7,8\}\) na \(4\) podzbiory: \(\{1,5,7,8\},\) \(\{2\},\) \(\{3,4\},\) \(\{6\}.\)
Dodajmy sztuczny \((n+1)\)-szy wiersz i ponumerujmy kolumny półszachownicy od prawej do lewej, zaczynając od \(2.\) Teraz półszachownica składa się z wszystkich pól o współrzędnych \((i,j),\) gdzie \(1 \le i < j \le n+1\) (pierwsza współrzędna odpowiada wierszowi, a druga kolumnie). Postawienie wieży w \(i\)-tym wierszu będziemy teraz odczytywać jako informację, która liczba jest po \(i\) w jej podzbiorze. Jeżeli wieża stoi na polu \((i,j),\) to po \(i\) jest \(j\) (np. wieża na polu \((1,5)\) oznacza, że po \(1\) jest \(5\)). Z kolei jeżeli \(i\)-ty wiersz jest pusty, to \(i\) jest ostatnią liczbą w swoim podzbiorze. Z faktu, że wieże się nie atakują, wiemy, że te informacje są niesprzeczne – nie więcej niż raz wskażemy poprzednika i następnika każdej liczby. Łącząc te fakty, dostajemy pewien podział zbioru \(\{1,\dots,n+1\}.\) Na ile części? Tyle, ile wierszy jest bez wież, czyli dokładnie \(n+1-k.\) Dokładnie tak, jak miało wyjść!
Z różnych rozstawień wież oczywiście wyjdą różne podziały. Ale czy dostaniemy je wszystkie? No tak, bo łatwo wskazać konstrukcję działającą w drugą stronę: z podziału możemy dostać rozstawienie nieatakujących się wież, po prostu wypisując pary elementów sąsiadujących w jego zbiorach, np. \(\{\{1\}, \{2,5,6,8\}, \{3\}, \{4,7\}\}\) da nam wieże \((2,5), (5,6), (6,8), (4,7).\) I to kończy nasz piękny dowód.
