* Zakład Fizyki Teoretycznej, Narodowe Centrum Badań Jądrowych
Gdy chcemy opisywać układy wielu cząstek kwantowych, jednym z fundamentalnych problemów, jaki napotykamy, jest ich nierozróżnialność. W przypadku obiektów makroskopowych (tzn. takich, które są dobrze opisywane w języku mechaniki klasycznej), nawet gdy są one identyczne (masa, rozmiary, ładunek), możemy je odróżniać na podstawie ich trajektorii. Dla każdego z takich ciał możemy bowiem napisać dynamiczne równanie ruchu. W ten sposób każdy obiekt makroskopowy ma swoje położenie, prędkość… i staje się unikatowy. Metoda ta zawodzi w przypadku obiektów kwantowych, gdyż tu możemy operować jedynie pojęciem prawdopodobieństwa tego, że ciało znajduje się w jakimś obszarze przestrzeni. Traci zatem sens również pojęcie trajektorii takiej cząstki\(^\dagger.\) Zamiast tego posługujemy się pewnym tworem matematycznym nazywanym funkcją falową, oznaczaną najczęściej grecką literą \(\psi.\) Konkretną postać \(\psi\) znajdujemy jako rozwiązanie fundamentalnego dla mechaniki kwantowej równania falowego – równania Schrödingera. Sama funkcja falowa nie ma prostej interpretacji fizycznej, lecz już kwadrat jej modułu \(|\psi(x)|^2\) wyraża gęstość prawdopodobieństwa znalezienia cząstki w punkcie \(x.\) Oznacza to, że zamiast mówić o położeniu cząstki czy też o jej pędzie, jesteśmy w stanie wyrokować jedynie o tym, jaki przedział położeń/pędów jest bardziej prawdopodobny od innych.
\(^\dagger\)Wyznacza się wprawdzie przybliżone trajektorie cząstek naładowanych w komorze dryfowej. Jest to jednak nadal trajektoria w rozumieniu mechaniki klasycznej.
Opisując stan układu wielu cząstek kwantowych, z uwagi na ich nierozróżnialność, zobligowani jesteśmy do traktowania go jako całości. Tak samo funkcja falowa opisująca stan takiego układu musi zależeć np. od położeń wszystkich składników (możemy również używać opisu w przestrzeni pędów).
Potencjał harmoniczny opisuje sytuację, w której energia potencjalna cząstki jest proporcjonalna do funkcji \(V(x)=\frac{1}{2}x^2.\) Funkcja ta ma minimum w punkcie \(x=0.\) Punkt ten nazywamy położeniem równowagi – aby wyprowadzić cząstkę z tego punktu, należy dostarczyć energię proporcjonalną do kwadratu wychylenia \(x^2.\) Taka zależność energii potencjalnej od wychylenia oznacza, że siła, która działa na cząstkę, jest proporcjonalna do wychylenia \(x,\) ale z ujemnym współczynnikiem (siła ma zwrot przeciwny do wychylenia). Czytelnik znający podstawy mechaniki klasycznej zapewne wie, że ,,siła równa jest minus gradientowi potencjału”, a gradient to w jednym wymiarze po prostu pochodna.
W fizyce klasycznej potencjał harmoniczny opisuje układ wykonujący drgania wokół położenia równowagi, czyli tzw. oscylator harmoniczny.
Wykonajmy pewien eksperyment (póki co myślowy). Wyobraźmy sobie dwie cząstki, które mogą poruszać się wzdłuż prostej (czyli tylko w jednym wymiarze). Na obie cząstki będzie działała siła zależna od położenia, która przyciąga cząstki do ustalonego położenia równowagi (opisywana tzw. potencjałem harmonicznym, patrz margines). Interesuje nas, jaki będzie przestrzenny rozkład tych dwóch cząstek. Gdyby chodziło o dwa ciała podlegające mechanice Newtona (np. dwie identyczne kulki), bez trudu pokazalibyśmy, że ulokują się one możliwie blisko minimum potencjału, jedynym zaś ograniczeniem są ich niezerowe promienie, stad też \(x_1\to0^-,\) \(x_2\to0^+,\) a środek masy układu znajduje się dokładnie w zerze.
Jeśli jednak nasze cząstki przejawiają naturę kwantową, wtedy musimy szukać stanu takiego układu dwucząstkowego, który zależał będzie od dwóch współrzędnych (położeń): \(\psi(x_1,x_2).\) Jeśli uda nam się wyznaczyć taką funkcję, to kwadrat jej modułu wskaże, dla jakich położeń \(x_1, x_2\) gęstość prawdopodobieństwa osiąga maksimum. Jak to ma miejsce dla niezależnych zdarzeń losowych, możemy przedstawić naszą funkcję w postaci iloczynowej: \(\psi(x_1,x_2)=\phi_a(x_1)\phi_b(x_2),\) gdzie \(\phi_{a,b}(x)\) jest tak zwaną funkcją jednocząstkową – czymś, co w naszym przykładzie odpowiada pojedynczej cząstce w pułapce. Taki opis byłby w pełni słuszny, gdyby nasze cząstki były rozróżnialne. Znaczy on bowiem, że cząstka pierwsza jest w stanie \(a,\) cząstka druga zaś w stanie \(b.\) Ów stan może oznaczać np. energię cząstki. Tak długo, jak cząstki są nierozróżnialne, trzeba wziąć pod uwagę, że możliwa jest także sytuacja odwrotna: cząstka pierwsza jest w stanie \(b,\) a druga w stanie \(a.\) Sama operacja zamiany cząstek (oznaczmy ją jako operację \(\hat{P}\)) jest równoważna przemnożeniu funkcji falowej przez pewną stałą \(c\): \[\hat{P}\psi(x_1,x_2)=c\cdot \psi(x_2,x_1).\] Gdy wykonamy tę operację dwukrotnie, wracamy do stanu początkowego: \[\hat{P}[\hat{P}\psi](x_1,x_2)=c^2\cdot \psi(x_1,x_2)=\psi(x_1,x_2),\] co nakłada ograniczenie: \(c=\pm1.\) Można się było spodziewać, że \(|c|=1,\) gdyż przestawienie nierozróżnialnych cząstek nie może zmieniać wartości prawdopodobieństwa. Mamy więc dwie możliwe sytuacje odpowiadające dwóm możliwym wartościom stałej \(c=\pm1\): \[\begin{aligned} \psi_{S}(x_1,x_2)&=\frac{1}{\sqrt2}\big(\phi_a(x_1)\phi_b(x_2)+\phi_b(x_1)\phi_a(x_2)\big),\\ \psi_{A}(x_1,x_2)&=\frac{1}{\sqrt2}\big(\phi_a(x_1)\phi_b(x_2)-\phi_b(x_1)\phi_a(x_2)\big). \end{aligned}\] Występujące powyżej suma i różnica mają fundamentalne znaczenie. W celu lepszego zrozumienia tego zagadnienia spójrzmy na rozkłady prawdopodobieństwa dla stanu symetrycznego \(S\) i antysymetrycznego \(A,\) gdy \(\phi_{a}(x)\) oraz \(\phi_{b}(x)\) są, odpowiednio, stanem podstawowym (stanem o najniższej energii) i pierwszym stanem wzbudzonym kwantowego oscylatora harmonicznego: \[\phi_a(x)=\frac{1}{\sqrt[4]{\pi}}e^{-x^2/2},\ \ \ \phi_b(x)=\frac{\sqrt{2}}{\sqrt[4]{\pi}}xe^{-x^2/2}.\] Rozkłady gęstości prawdopodobieństwa zostały przedstawione na rysunku 1. Gdy je porównamy, możemy zaobserwować pewne fundamentalne różnice. Podczas gdy funkcja \(|\psi_S(x_1,x_2)|^2\) osiąga maksimum dla \(x_1=x_2=\pm\frac{1}{\sqrt2}\) oraz przyjmuje zerową wartość na prostej \(x_1=-x_2,\) to w wypadku funkcji \(|\psi_A(x_1,x_2)|^2\) sytuacja jest odwrotna. Oznacza to, że jeśli nasze cząstki będą się znajdowały w stanie opisywanym funkcją symetryczną – będą chciały przebywać w tym samym miejscu, natomiast cząstki opisywane funkcją antysymetryczną ,,wybiorą” przeciwne zbocza pułapki, zaś prawdopodobieństwo zaobserwowania ich razem jest zerowe – jest to zdarzenie niemożliwe.
Mówimy, że funkcja \(\psi_{S}(x_1,x_2)\) opisuje stan symetryczny, ponieważ zamiana cząstek, której odpowiada zamiana argumentów \(x_1\leftrightarrow x_2,\) pozostawia funkcję \(\psi_{S}(x_1,x_2)\) niezmienioną. Natomiast zamiana cząstek (czyli argumentów \(x_1\leftrightarrow x_2\)) funkcji \(\psi_{A}(x_1,x_2)\) zmienia jej znak na przeciwny, dlatego stan opisywany tą funkcją nazywamy antysymetrycznym.
Energia cząstek w potencjale harmonicznym jest skwantowana, podobnie jak energia elektronu w atomie wodoru – cząstka może znajdować się w stanach o pewnych wyróżnionych energiach. Stan o najniższej energii nazywamy podstawowym, a stany o wyższych energiach nazywamy wzbudzonymi. Podane tu funkcje \(\phi_a(x)\) oraz \(\phi_b(x)\) znajduje się jako rozwiązania wspomnianego już wcześniej równania Schrödingera z potencjałem harmonicznym, odpowiadające energii stanu podstawowego i pierwszej dozwolonej wartości energii większej od wartości najniższej.
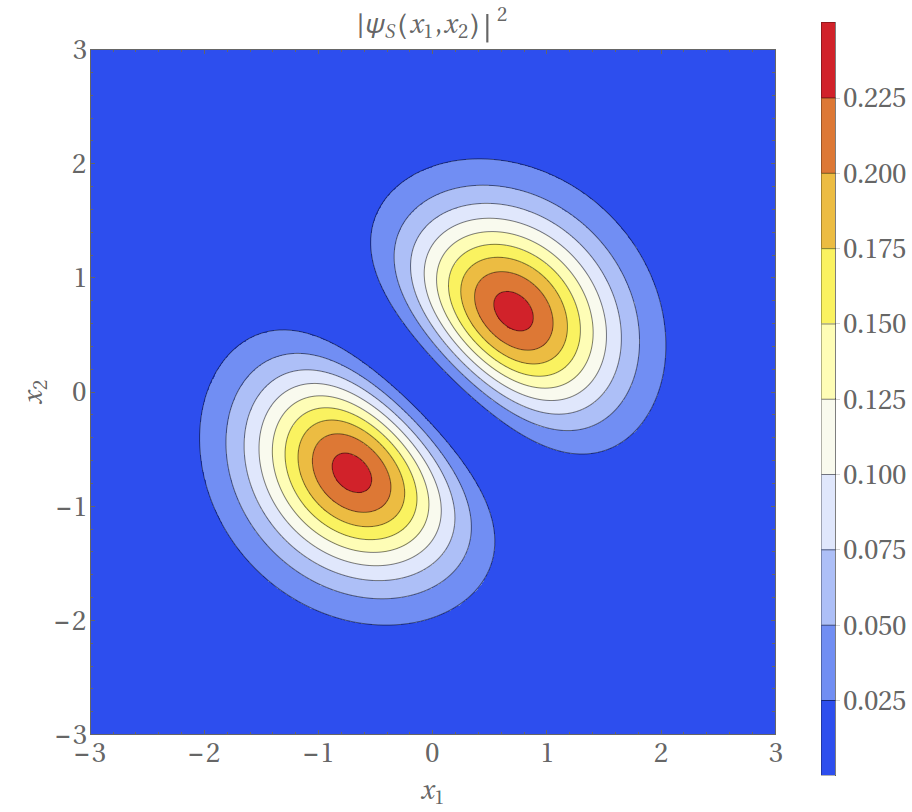
Rys. 1. Rozkład gęstości prawdopodobieństwa \(p(x_1,x_2)\) dla dwóch cząstek w polu jednowymiarowego oscylatora harmonicznego.
Górny rysunek: przypadek symetryczny – prawdopodobieństwo jest maksymalne dla jednakowych położeń cząstek \((x_1=x_2=\pm 1/\sqrt 2).\)
Dolny rysunek: przypadek antysymetryczny – prawdopodobieństwo jest maksymalne dla przeciwnych położeń cząstek \(x_1=-x_2=\pm 1/\sqrt{2}\)
Rodzi się zatem pytanie: Który z wariantów (symetryczny czy antysymetryczny) będzie się realizował? Kluczową rolę w znalezieniu odpowiedzi odgrywa własność kwantowa zwana spinem, którą czasem (niezbyt słusznie) określa się jako własny moment pędu. De facto spin, będący immanentną cechą danej cząstki, pozwala wyróżnić dwa rodzaje cząstek: o spinie całkowitym (np. fotony) oraz te o spinie połówkowym (np. elektrony, protony czy neutrony). Pierwsze z nich, nazywane bozonami (Satyendra Nath Bose wyznaczył rozkład prawdopodobieństwa dla fotonów), opisywane są symetryczną funkcją falową. Mogą więc wszystkie znajdować się w tym samym stanie kwantowym (taki stan materii nazywamy kondensatem Bosego–Einsteina). Drugie określamy jako fermiony (od nazwiska Enrico Fermiego). W pewnych szczególnych warunkach bozony mogą tworzyć kondensat, natomiast fermiony są zawsze unikatowe: nie jest możliwa sytuacja, w której jakiś stan kwantowy jest obsadzony przez więcej niż jeden fermion. Zapisana powyżej własność stanowi treść zakazu Pauliego oraz wskazuje na niezwykle istotną korelację między cząstkami, które mu podlegają.
Zakaz Pauliego jest przyczyną tego, że elektrony (które są fermionami) w atomach obsadzają kolejne coraz wyższe poziomy energetyczne. Gdyby elektrony były bozonami, to wszystkie znajdowałyby się w jednym i tym samym stanie o najniższej energii i nie byłoby chemii, jaką znamy, a zatem nas też by nie było.
Powyższy przykład dwóch cząstek jest relatywnie prosty w analizie i pozwala na zrozumienie, jak wielką rolę odgrywa symetria funkcji falowej i związany z nią zakaz Pauliego. Gdy zwiększymy liczbę atomów oraz gdy nasza pułapka jest przynajmniej dwuwymiarowa, zagadnienie staje się nietrywialne. Z jednej strony mamy do czynienia z ,,odpychaniem” się atomów (jest to wynik wielocząstkowych korelacji, a nie żadne z podstawowych oddziaływań, gdyż atomy nie posiadają ładunku), z drugiej zaś zewnętrzny potencjał nie pozwala im zbytnio się od siebie oddalić. Pojawia się zatem pytanie: Gdzie są te atomy i jak się unikają wzajemnie w przestrzeni? To pytanie zadali sobie uczeni z Instytutu Fizyki Polskiej Akademii Nauk, przystępując do badania tego, czy są jakieś geometrycznie preferowane ustawienia cząstek oraz jak bardzo te ustawienia są preferowane w stosunku do innych [3, 7, 1, 4].
Postaram się pokrótce wyjaśnić główne założenia oraz rezultaty cytowanych prac. Niestety wraz ze wzrostem liczby atomów rośnie także stopień złożoności rozważanego zagadnienia. Dla \(N\) cząstek w 2-wymiarowej pułapce mamy już \(2N\) zmiennych, od których zależy pełna funkcja falowa, a w konsekwencji prawdopodobieństwo. Funkcja falowa może zostać przedstawiona w postaci iloczynowej, jednak należy wziąć pod uwagę wszystkie możliwe permutacje zbioru \(N\)-elementowego z uwzględnieniem zmiany znaku iloczynu przy każdorazowej zamianie cząstek. O ile było to trywialne dla \(N=2,\) gdyż istnieją tylko \(2!=2\) permutacje (którym odpowiadają dwa składniki w funkcji falowej \(\psi_A\)), to już dla \(N=3\) mamy \(3!=6\) składników. Tak jak w przypadku opisanej wcześniej funkcji \(\psi_A\) dla przypadku \(N=2,\) w ogólnym przypadku funkcja falowa będzie sumą \(N!\) składników, z których każdy jest iloczynem \(N\) funkcji jednocząstkowych. Kolejność argumentów \(\vec{r}_i\) w każdym składniku jest inna – kolejności te odpowiadają wszystkim możliwym permutacjom, a dodatkowo każdy składnik mnożony jest przez znak permutacji. Na koniec funkcję trzeba unormować, czyli podzielić przez \(\sqrt{N!},\) żeby kwadrat jej modułu opisywał gęstość prawdopodobieństwa.
Opisaną w tekście procedurę konstruowania całkowicie antysymetrycznej funkcji falowej \(N\) cząstek można zapisać w postaci tzw. wyznacznika Slatera (wyznacznika macierzy zbudowanej z funkcji jednocząstkowych): \[\begin{aligned} &\psi(\vec{r}_1,\vec{r}_2,\ldots\vec{r}_N)=\\ &\frac{1}{\sqrt{N!}}\left| \begin{array}{cccc} \phi_1(\vec{r}_1) &\phi_2(\vec{r}_1)&\cdots& \phi_N(\vec{r}_1)\\ \phi_1(\vec{r}_2) &\phi_2(\vec{r}_2)&\cdots& \phi_N(\vec{r}_2)\\ \vdots &\vdots &\cdots & \vdots\\ \phi_1(\vec{r}_N) &\phi_2(\vec{r}_N)&\cdots& \phi_N(\vec{r}_N) \end{array}\right| \end{aligned}\]
Poszukiwanie maksimum prawdopodobieństwa z matematycznego punktu widzenia jest zdecydowanie trudniejsze, lecz ciągle wykonalne. Posłużyć się można np. metodą Monte Carlo [6]. Polega ona na tym, że rozpoczyna się od losowej konfiguracji atomów, a następnie dodaje niewielkie przesunięcia (tylko jednego w każdej iteracji), sprawdzając, czy taka modyfikacja prowadzi do wzrostu wartości prawdopodobieństwa (zachowujemy wtedy taką konfigurację), czy też do jego obniżenia (odrzucamy taką konfigurację). Proces ten jest wielokrotnie powtarzany z coraz mniejszą amplitudą przesunięć, aż do uzyskania satysfakcjonującej zbieżności. Otrzymywane w ten sposób położenia atomów w przestrzeni dwuwymiarowej (były również prowadzone badania w trzech wymiarach [2]) tworzą struktury geometryczne, które nazywamy kryształami Pauliego.
Co oznacza ,,pełne obsadzenie” stanu energetycznego? W przypadku pułapki jednowymiarowej każdej energii odpowiada jeden stan wzbudzony. W przypadku pułapki dwu- (i więcej) wymiarowej energie wzbudzeń w różnych kierunkach się dodają, a w konsekwencji tę samą energię mogą mieć różne stany. Na przykład pierwszej wzbudzonej energii w pułapce dwuwymiarowej odpowiadają dwa stany wzbudzone – cząstka może drgać w kierunku \(x\) lub \(y.\) Oba stany mają tę samą energię, ale są to różne stany. Drugiej energii wzbudzonej odpowiadają już trzy stany, ponieważ cząstka może być w drugim stanie wzbudzonym w kierunku \(x\) i w stanie podstawowym w kierunku \(y,\) lub na odwrót, a dodatkowo może być w pierwszym stanie wzbudzonym w obu kierunkach – wtedy energie tych wzbudzeń się sumują, a jak wiadomo \(1+1=2,\) i dostajemy trzeci stan odpowiadający drugiemu poziomowi wzbudzonemu. Wyższe stany wzbudzone otrzymuje się w analogiczny sposób. Trzeciemu wzbudzonemu poziomowi energetycznemu odpowiadają 4 stany, gdyż \(3=3+0=2+1=1+2=0+3,\) a składniki sumy odpowiadają energiom drgań w kierunkach \(x\) i \(y,\) czwartemu odpowiada 5 stanów itp.
Pełne obsadzenie oznacza, że mamy obsadzone na przykład dwa pierwsze stany – podstawowy i dwa odpowiadające pierwszemu stanowi wzbudzonemu, co łącznie daje trzy cząstki. Kolejne w pełni obsadzone konfiguracje powstają przez dodanie cząstek obsadzających całkowicie następne stany energetyczne, czyli możemy dodać trzy cząstki, żeby obsadzić drugi poziom wzbudzony (razem 6 cząstek), następnie dodać 4, żeby obsadzić trzeci (razem 10 cząstek), następnie 5 (razem 15 cząstek) itd.
Kolejny problem polega na tym, że dokonując pomiaru położeń wielu cząstek (np. przy pomocy tablicy detektorów) oraz powtarzając te pomiary wielokrotnie z uwagi na statystyczny charakter procesu (atomy wcale nie muszą przebywać w położeniach odpowiadających wcześniej wyznaczonemu maksimum), w granicy nieskończonej liczby powtórzeń otrzymamy średnią, która będzie jednocząstkowym rozkładem prawdopodobieństwa: \[p(x,y)=\sum_{n=1}^N{|\phi_n(x,y)|^2}.\] Informacja o korelacjach między atomami zostaje w tym wypadku utracona poprzez uśrednienie po wielu realizacjach, tj. wynikach poszczególnych pomiarów.
Z tego względu taki pomiar nie pozwoli na poznanie geometrycznego rozkładu atomów w pułapce. Konieczne jest sięgnięcie po narzędzie bardziej wyrafinowane niż wielokrotny pomiar położeń atomów. Narzędziem tym jest wprowadzenie rozkładu konfiguracji. W celu jego otrzymania każdy wynik uzyskany z rozkładu \(N\)-cząstkowego jest przekształcany izometrycznie – poprzez obrót o pewien kąt (z zachowaniem położenia środka masy), tak aby otrzymać rozkład położeń atomów możliwie najbliższy temu, który wynika z maksymalizacji prawdopodobieństwa opisanego tym rozkładem (przewidzianej struktury kryształu Pauliego). Dopiero takie wyniki podlegają uśrednieniu, tworząc nowy rozkład \(C(x,y).\)
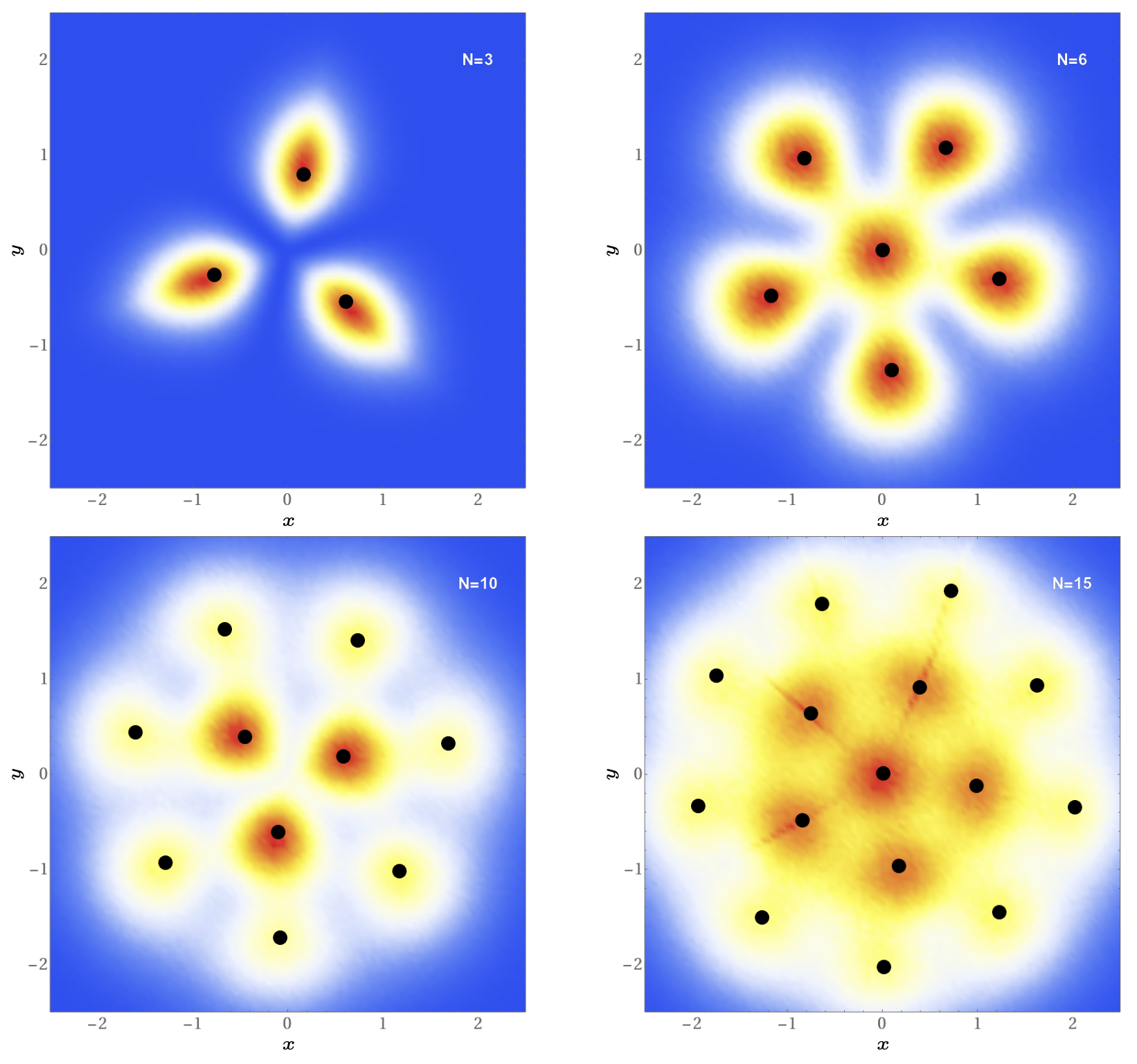
Przykłady rozkładów gęstości konfiguracji \(C(x,y)\) otrzymane dla \(N=3,6,10,15\) zostały przedstawione na rysunku 2. Wybrane liczby atomów odpowiadają sytuacjom, gdy w pełni są obsadzone kolejne stany energetyczne (patrz margines), dlatego też obserwowane struktury odzwierciedlają symetrię osiową pułapki. Nie dzieje się tak jednak dla dowolnego \(N,\) kiedy to atomy o największej energii mogą obsadzać różne stany własne pułapki. W takiej sytuacji struktura kryształu Pauliego nie jest jednoznacznie określona.
Na rysunku 2 widoczna jest wyraźna struktura powłokowa, jednakże powłoki w krysztale nie są tożsame z powłokami energetycznymi, charakterystycznymi dla elektronów w atomie. Nie są to także powłoki o określonym promieniu, gdyż w miarę wzrostu liczby atomów tworzących kryształ Pauliego pojawiają się pewne fluktuacje, zależne m.in od rozkładu atomów na powłoce bliższej środka masy. Wszystkie te cechy dowodnie wskazują, że istnienie korelacji \(N\)-tego rzędu (bo każdy atom jest skorelowany z \(N-1\) pozostałymi), wynikających z zakazu Pauliego, prowadzi do powstawania bardzo egzotycznych układów atomów, które wykazują jednak pewne uporządkowania – dokładnie tak, jak w strukturach krystalicznych.
Literatura
[1] M. Gajda, J. Mostowski, M. Pylak, T. Sowiński, and M. Załuska-Kotur. Pauli crystals–interplay of symmetries. Symmetry, 12(11), 2020.
[2] M. Gajda, J. Mostowski, T. Sowiński, and M. Załuska-Kotur. Pauli crystals: hidden geometric structures of the quantum statistics, 2015.
[3] M. Gajda, J. Mostowski, T. Sowiński, and M. Załuska-Kotur. Single-shot imaging of trapped fermi gas. Europhysics Letters, 115(2):20012, aug 2016.
[4] F. Gampel, M. Gajda, M. Załuska–Kotur, and J. Mostowski. Pauli crystals in harmonic trap and on a sphere. Physics Letters A, 422:127799, 2022.
[5] M. Holten, L. Bayha, K. Subramanian, C. Heintze, P. M. Preiss, and S. Jochim. Observation of pauli crystals. Phys. Rev. Lett., 126:020401, Jan 2021.
[6] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller. . The Journal of Chemical Physics, 21(6):1087–1092, 12 1953.
[7] D. Rakshit, J. Mostowski, T. Sowiński, M. Załuska-Kotur, and M. Gajda. On the observability of pauli crystals in experiments with ultracold trapped fermi gases. Scientific Reports, 7(1):15004, Nov 2017.
W ostatnim czasie grupie badaczy z Heidelbergu udało się eksperymentalnie potwierdzić istnienie przedstawionych powyżej struktur [5]. Wykorzystano do tego celu ultrazimny i rozrzedzony gaz atomów \(^6\)Li. Dokonując wielokrotnych rekonstrukcji rozkładu gęstości pędów atomów poprzez pomiar tzw. czasu przelotu TOF, time of flight, oraz przeprowadzając analizę analogiczną do opisanej w tekście, udało się wyznaczyć rozkład konfiguracji, który okazał się całkowicie zgodny z teoretycznymi przewidywaniami.