Afiliacja: Wydział Matematyki i Informatyki, Uniwersytet Jagielloński
Jedną z największych różnic pomiędzy matematykami współczesnymi a tymi sprzed stuleci jest wąska specjalizacja tych pierwszych. Z biografii gigantów, takich jak Euler, Gauss czy Riemann, jasno wyłania się obraz matematyków wszechstronnych, zajmujących się wszystkimi dziedzinami ówczesnej królowej nauk. Ich następcy, oczywiście z pewnymi chwalebnymi (lecz jakże rzadkimi) wyjątkami, są tak wąsko wyspecjalizowani, że często nie potrafią zrozumieć wyników swoich kolegów z innych dziedzin.
Częściowo z tego powodu w matematyce współczesnej bardzo poczesne miejsce zajmują teorie, w których wykorzystuje się narzędzia z różnych dziedzin. Przykładem znanym ze szkoły są funkcje wypukłe, które można scharakteryzować geometrycznie, ale także, zakładając odpowiednią regularność, w sposób czysto analityczny – druga pochodna takiej funkcji musi być wszędzie nieujemna.
Geometryczna charakteryzacja funkcji wypukłych jest prosta: zbiór nad ich wykresem jest wypukły. Zbiór natomiast nazywamy wypukłym, jeśli wraz z każdą parą swoich punktów \(p,q\) zawiera cały odcinek łączący \([p,q].\)
W tekście tym przedstawione zostanie twierdzenie dotyczące tak zwanej funkcji odległości, które także wiąże wypukłość z pewnymi faktami z analizy matematycznej. Tym razem jednak głównym aktorem będzie pierwsza pochodna zamiast drugiej. Oto i główne danie w menu:
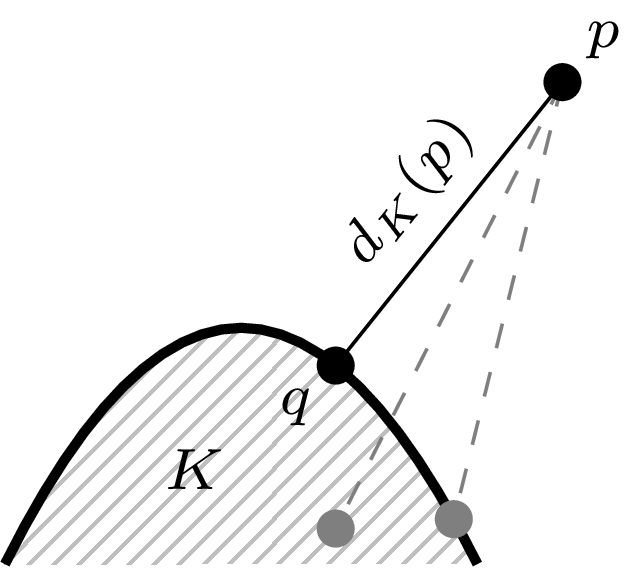
Twierdzenie (Motzkina). Niech \(K\) będzie domkniętym podzbiorem płaszczyzny, a \(d_K\) funkcją mierzącą odległość od zbioru \(K\): \[d_K(p) = \min \lbrace \| p-q \| \ | \ q \in K \rbrace \ \ \ \ \ \ \text{(zob. rys. 1)}.\] Wówczas zbiór \(K\) jest wypukły wtedy i tylko wtedy, gdy funkcja odległości \(d_K\) jest różniczkowalna na dopełnieniu \(K,\) czyli na zbiorze \(\mathbb{R}^2 \setminus K.\)
Rys. 1. Punkt \(q\) jest najbliżej \(p\) spośród wszystkich punktów zbioru \(K\)
Symbolem \(\| (x_1,x_2) \|\) oznaczamy wielkość \(\sqrt{x_1^2+x_2^2},\) dzięki czemu \(\| p-q \|\) jest długością odcinka łączącego \(p\) i \(q.\)
Aby uniknąć rozważań filozoficznych nad zbiorami pustymi, zakładamy także, że zbiór \(K\) i jego dopełnienie są niepuste.
Jest to dość niezwykły fakt wiążący geometrię \(K\) z regularnością \(d_K.\) Otóż na oko wydawać się może, że za regularność funkcji \(d_K\) powinna odpowiadać gładkość brzegu \(K,\) a nie geometryczny kształt. Zanim jednak zagłębimy się w meandry tegoż twierdzenia, starannie wyjaśnijmy wszystkie pojęcia, aby nie było nieporozumień. Polecam również lekturę artykułu Michała Miśkiewicza z \(\Delta^2_{24}\) pt. Babo, babo, udaj się.
Na początek przypomnijmy, czym jest domkniętość: intuicyjnie zbiory domknięte to te, które zawierają swój brzeg (pełna definicja widnieje obok). Do czego przyda nam się to pojęcie? Zobaczymy za chwilę.
Definicja. Zbiór \(K\) punktów na płaszczyźnie nazywamy zbiorem domkniętym, jeżeli posiada on następującą własność: dla dowolnego punktu \(p\) z dopełnienia \(K\) istnieje promień \(r > 0\) oraz koło \(B_r(p)\) (bez okręgu na brzegu) w całości zawarte w tym dopełnieniu.
Wytrawny Czytelnik spostrzeże w definicji funkcji \(d_K\) pewną subtelność: czemu niby wartość minimum musiałaby istnieć, skoro bierzemy ją po zbiorze, który wcale skończony być nie musi? Otóż właśnie tu interweniuje (po raz pierwszy) domkniętość – jeżeli weźmiemy ciąg punktów \(q_j\) z \(K,\) które prawie realizują minimum i są coraz bliżej tego celu, to okaże się, że pewien podciąg punktów \(q_j\) będzie zbieżny do jakiegoś punktu \(\hat{q}\in K.\) Okazuje się, że \(\hat{q}\) będzie realizować minimum! Szczegóły tego rozumowania pozostawiamy Ambitnym Czytelnikom jako ciekawe ćwiczenie.
Zbieżność \(q_j \to \hat{q}\) oznacza, że obie współrzędne, traktowane jako ciągi liczbowe, są zbieżne.
Funkcję odległości definiuje się w miarę prosto, niestety gorzej jest z jej jawnym wyliczeniem. Na przykład dla koła domkniętego \(\overline{B}_r((0,0))\) da się to zrobić stosunkowo łatwo i wzór wygląda następująco: \[d_{\overline{B}_r((0,0))}(p) = \begin{cases} 0 & \text{dla } p \in \overline{B}_r((0,0)); \\ \| p \| - r & \text{w~przeciwnym przypadku.} \end{cases}\] Ambitnemu Czytelnikowi pozostawiamy wyliczenie \(d_K\) dla ciekawszych geometrycznych obiektów, choćby kwadratu \([-1,1]^2,\) który wymaga już rozpatrzenia większej liczby przypadków (rys. 2).
Rys. 2. Poziomice funkcji \(d_K\) w przypadku, gdy \(K\) jest kołem jednostkowym \(\overline{B}_1((0,0))\) i kwadratem \([-1,1]^2\)
Musimy także przypomnieć pojęcie różniczkowalności dla funkcji wielu zmiennych. Niestety, znany Czytelnikowi wzór \[f'(p) = \lim_{h \to 0}\frac{f(p+h)-f(p)}{h}\] nie da się zastosować, gdyż w przypadku wielu zmiennych parametr \(h\) byłby wektorem, zaś przez wektory dzielić nie wolno! Zmodyfikujmy więc nieco definicję:
Na płaszczyźnie problem dzielenia przez wektory można rozwiązać, traktując punkty jako liczby zespolone. W ten sposób uzyskalibyśmy definicję czegoś, co w matematyce nazywamy \(\mathbb C\)-różniczkowalnością. Ale to, jak mawiała Szeherezada, jest już temat na inne opowiadanie.
Definicja. Funkcję \(f \colon \mathbb{R}^2 \to \mathbb{R}\) nazywamy różniczkowalną w punkcie \(p = (p_1,p_2),\) jeżeli istnieją stałe \(a_1,a_2\) takie, że \[\lim_{h_1^2+h_2^2\rightarrow 0}\frac{|f((p_1+h_1,p_2+h_2))-f((p_1,p_2))-a_1h_1-a_2h_2|}{\| h \|} = 0.\] Funkcję nazywamy różniczkowalną na zbiorze \(U,\) jeżeli jest ona różniczkowalna w każdym punkcie zbioru \(U.\) Stałe \(a_1,a_2\) (oczywiście zależne od punktu \(p\)!) nazywamy pochodnymi cząstkowymi \(f\) w \(p\) i piszemy \(a_1=\frac{\partial f}{\partial x_1}(p),\ a_2=\frac{\partial f}{\partial x_2}(p).\)
Czy jest jakaś intuicja stojąca za tą, trochę zagmatwaną, definicją? Czytelnik zechce zauważyć, że płaszczyzna \(x_3 = f((p_1,p_2)) + a_1 (x_1-p_1) + a_2 (x_2-p_2)\) w \(\mathbb R^3\) będzie wtedy spełniać rolę stycznej do wykresu \(f\) w punkcie \((p_1, p_2).\) Tak więc różniczkowalność w danym punkcie jest równoważna istnieniu płaszczyzny stycznej do wykresu.
Staranne wyliczenie dla \(d_{\overline{B}_r((0,0))}\) pozwala stwierdzić, że na okręgu \({\lbrace x^2+y^2=r^2\rbrace}\) funkcja \(d_{\overline{B}_r((0,0))}\) nie jest różniczkowalna, natomiast jest różniczkowalna w dopełnieniu. Jeżeli Czytelnik uporał się z wyznaczeniem \(d_{[-1,1]^2},\) to zechce zauważyć, że brak gładkości na brzegu \([-1,1]^2\) nie wpływa, wbrew intuicji, na różniczkowalność \(d_{[-1,1]^2}\) w dopełnieniu!
Rozróżnienie punktów różniczkowalności i nieróżniczkowalności \(d_{\overline{B}_r((0,0))}\) i \(d_{[-1,1]^2}\) staje się jasne po spojrzeniu na rysunek 2.
Jesteśmy już gotowi do wyjaśnienia sobie, dlaczego geometria i analiza wiążą się w twierdzeniu Motzkina. Jak to w matematyce często bywa, powiązanie dwóch pozornie nieskorelowanych faktów najczęściej odbywa się poprzez przeformułowanie ich w nieco innym języku. Zacznijmy od strony geometrycznej:
Lemat. Zbiór \(K\) na płaszczyźnie jest wypukły wtedy i tylko wtedy, gdy dla dowolnego punktu \(p\) z dopełnienia istnieje dokładnie jeden punkt \(q \in K\) najbliższy punktowi \(p.\)
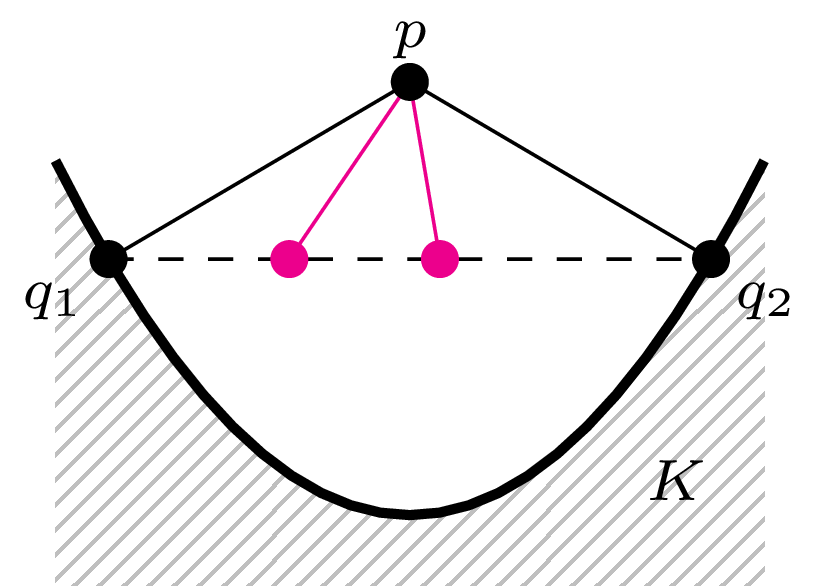
Jedna część lematu jest trywialna: jeżeli \(q_1\neq q_2\) są dwoma punktami z \(K\) (jednocześnie) najbliższymi do pewnego punktu \(p,\) to odcinek \([q_1,q_2]\) miałby kłopoty z wciśnięciem się do (wypukłego!) zbioru \(K\) (rys. 3).
Rys. 3. Jeśli punkty \(q_1,q_2\) są w tej samej odległości od \(p,\) to każdy inny punkt odcinka \([q_1,q_2]\) jest bliżej. Gdy \(K\) jest wypukły, to zgodnie z definicją zawiera cały ten odcinek
W drugą stronę jest ciekawiej. Przypuśćmy, że \(K\) nie jest wypukły, i weźmy dwa punkty \(q_1,q_2 \in K,\) dla których odcinek \([q_1,q_2]\) nie jest zawarty w \(K.\) Przecięcie odcinka \([q_1,q_2]\) z \(K\) może być skomplikowane, niemniej dzięki domkniętości \(K\) znajdziemy mniejszy odcinek \([l_1,l_2]\) zawarty w \([q_1,q_2],\) którego końce leżą w \(K,\) ale wnętrze jest już rozłączne z \(K.\)
– To wtedy środek odcinka \((l_1,l_2)\) da nam punkt \(p\) o dwóch najbliższych punktach do \(K\)! – może wykrzyknąć Czytelnik. Niestety nie jest to do końca poprawne, bo punkt \(p\) może mieć najbliższego towarzysza z \(K\) gdzieś jeszcze bliżej…
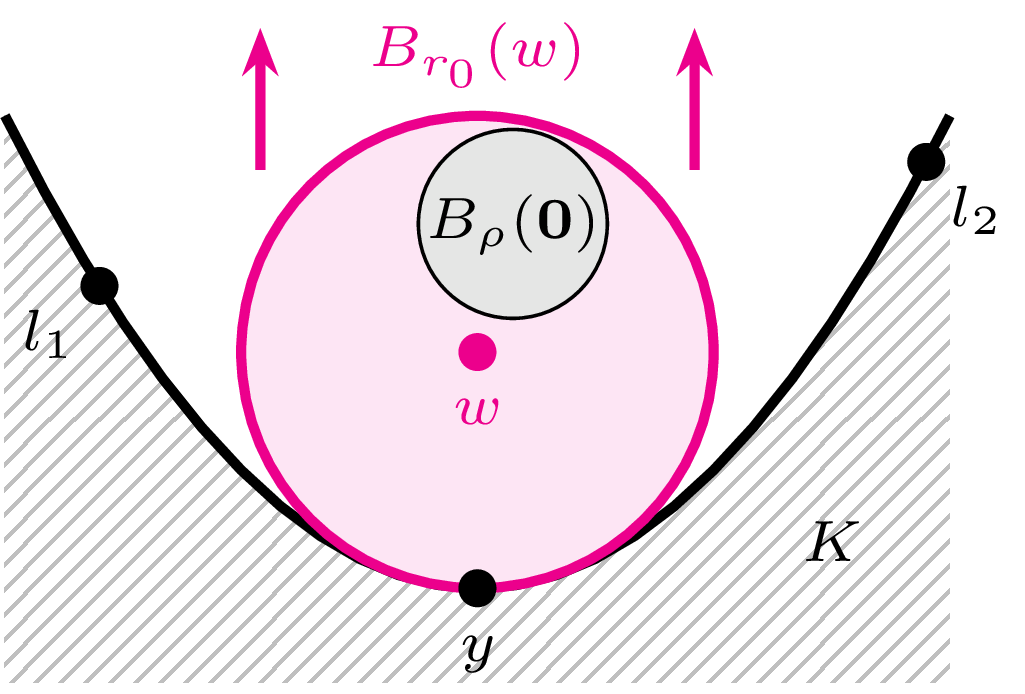
Bez straty ogólności umówmy się, że tak wybrany punkt \(p\) jest początkiem układu współrzędnych. Jako że należy on do dopełnienia (domkniętego) zbioru \(K,\) to pewna kula \(\overline{B}_{\rho}((0,0))\) o środku w \(p = (0,0)\) jest rozłączna z \(K.\) Rozpatrzmy teraz rodzinę kół \[\mathcal{F}= \lbrace B_r((x,y)) \ | \ B_\rho((0,0)) \subset B_r((x,y)), \ B_r((x,y)) \cap K = \emptyset \rbrace,\] czyli rodzinę kół zawierających \(B_\rho((0,0)),\) ale nadal rozłącznych z \(K.\) Wiemy już, że jest ona niepusta. Wybierzmy teraz z rodziny \(\mathcal{F}\) koło o największym promieniu – nazwijmy je \(B_{r_0}(w)\) (rys. 4). Oczywiście na okręgu brzegowym koła \(B_{r_0}(w)\) musi być pewien punkt \(y \in K.\) Wykażemy, że nie jest on jedyny. Przypuśćmy więc przeciwnie i przesuńmy koło \(\overline{B}_{r_0}(w)\) o \(\varepsilon>0\) w kierunku \(\overrightarrow{yw}.\) Jeżeli \(\varepsilon\) dobierzemy wystarczająco małe, to przesunięte koło będzie rozłączne z \(K.\) Jeśli ponadto nadal zawiera \(B_\rho((0,0)),\) to wystarczy je teraz nadmuchać (delikatnie – bez obawy, że pęknie, może jednak dotknąć \(K\)…), i dostaniemy sprzeczność z maksymalnością \(r_0.\) W ogólnym przypadku to dodatkowe założenie może nie być spełnione, bo koło \(\overline{B}_\rho((0,0))\) może dotykać brzegu \(B_{r_0}(w)\) w jakimś punkcie \(z\) – wówczas wystarczy nieznacznie poprawić procedurę i kierunek przesuwania zmienić z \(\overrightarrow{yw}\) na \(\overrightarrow{yz}.\)◻
Kolejne ciekawe zadanie dla Czytelnika – dlaczego w rodzinie \(\mathcal{F}\) istnieje koło o największym promieniu? Czy gdyby warunek \(B_\rho((0,0)) \subset B_r((x,y))\) zastąpić prostszym warunkiem \((0,0) \in B_r((x,y)),\) to coś by się zmieniło?
Znów pojawia się odwieczne pytanie: dlaczego przesunięcie \(\overline{B}_{r_0}(w)\) jest rozłączne z \(K\)? Istotna tu jest samotność \(y\) oraz (który to już raz!) domkniętość \(K.\)
Rys. 4. Spośród kół zawierających \(B_\rho((0,0))\) i rozłącznych z \(K\) to największe musi dotykać \(K\) w co najmniej dwóch punktach, inaczej dałoby się znaleźć większe
Powyższy dowód jest nieco zagmatwany – można go znaleźć na przykład w książce Hörmandera [H, Th. 2.1.30]. Być może Czytelnik znajdzie prostszy? W każdym razie mamy już opis geometryczny za pomocą odległości – pozostaje analiza. Poniższy lemat zakończy dowód twierdzenia Motzkina:
Lemat. Niech \(K\) będzie domkniętym podzbiorem płaszczyzny. Funkcja \(d_K\) jest różniczkowalna w punkcie \(p\in\mathbb R^2 \setminus K\) wtedy i tylko wtedy, gdy najbliższy do \(p\) punkt zbioru \(K\) jest wyznaczony jednoznacznie.
Dowód przeprowadzimy dla \(d_K^2\) (czyli kwadratu odległości od \(K\)) zamiast dla \(d_K,\) gdyż bez kwadratu musielibyśmy się uporać z różniczkowaniem pierwiastków, co nie jest zbyt przyjemne. Na szczęście, dla funkcji dodatnich (a taka jest \(d_K\) na \(\mathbb{R}^2 \setminus K\)) różniczkowalność funkcji jest równoważna różniczkowalności jej kwadratu.
Także i tym razem mamy do wykazania dwie implikacje, przy czym jedna z nich jest bardzo łatwa. Przypuśćmy, że \(d_K\) jest funkcją różniczkowalną w punkcie \(p\) i niech \(q\) będzie najbliższym do \(p\) punktem z \(K.\) Chcemy wykazać, że \(q\) jest wyznaczony jednoznacznie. Do tego celu skonstruujmy funkcję \[f(w) := \| w-q \|^2 - d_K^2(w) = (w_1-q_1)^2+(w_2-q_2)^2 - d_K^2(w).\] Jest to funkcja nieujemna (dlaczego?), a dodatkowo zeruje się ona w \(p,\) czyli ma w \(p\) minimum lokalne. Dla różniczkowalnych funkcji jednej zmiennej oznacza to zerowanie się pochodnej. A jak jest w przypadku dwóch (lub wielu) zmiennych? Przypomnijmy interpretację za pomocą płaszczyzny stycznej – w punkcie minimum płaszczyzna ta musi być pozioma, co w języku analizy oznacza, że pochodne cząstkowe są zerowe: \(\frac{\partial f}{\partial x_1}(p) = 0,\) \(\frac{\partial f}{\partial x_2}(p) = 0.\) Bezpośrednim rachunkiem sprawdzamy, że te równości można zapisać następująco: \[2(p_1-q_1) = \frac{\partial d_K^2}{\partial x_1}(p); \ \ \ 2(p_2-q_2) = \frac{\partial d_K^2}{\partial x_2}(p).\] Te wzory jednoznacznie wyznaczają punkt \(q = (q_1,q_2).\)
I tym razem w drugą stronę jest ciekawiej. Przyda nam się także trochę notacji: przez \(\langle p,q \rangle\) oznaczmy iloczyn skalarny \(p = (p_1,p_2)\) oraz \(q = (q_1,q_2)\) (traktowanych jako wektory na płaszczyźnie), czyli \(p_1q_1 + p_2q_2\); zauważmy, że \(\| p \|^2 = \langle p, p \rangle.\) Będziemy pisać, że jakieś wyrażenie \(l(h)\) jest \(o(h)\) (czytamy: o małe od \(h\)) jeżeli \(\lim_{h_1^2+h_2^2 \to 0}\frac{l(h)}{\| h \|}=0.\)
Niech więc dla ustalonego \(p \in \mathbb{R}^2 \setminus K\) punkt \(q\) będzie jedynym najbliższym z \(K.\) Dowód pierwszej implikacji mówi nam, że jeśli funkcja \(d_K^2\) jest różniczkowalna w \(p,\) to jej pochodnymi cząstkowymi są \(2(p_1-q_1)\) i \(2(p_2-q_2).\) Pozostaje nam więc podstawić te wartości do definicji i sprawdzić zbieżność odpowiedniego ilorazu. Przy użyciu naszej notacji zbieżność ta wyraża się następująco: wyrażenie \(d_K^2(p+h) - d_K^2(p) - 2 \langle p-q,h \rangle\) jest \(o(h).\)
Do dzieła! Funkcja \(d_K\) jest ciągła, a więc jeżeli wektor \(h\) jest wystarczająco krótki, to punkt \(p+h\) po pierwsze będzie w \(\mathbb{R}^2 \setminus K,\) a po drugie będzie istniał (niekoniecznie jedyny!) punkt \(q_h \in K\) najbliższy do \(p+h,\) przy czym \(q_h\) musi zbiegać do \(q,\) gdy \(h_1^2+h_2^2 \to 0\) (wyjaśnienie tych szczegółów pozostawiamy Czytelnikowi jako ćwiczenie). Dopełniając do kwadratu, otrzymujemy: \[\begin{aligned} d_K^2(p+h) - d_K^2(p) - 2 \langle p-q,h \rangle &= \| p+h-q_h \|^2 - \| p-q \|^2 - 2 \langle p-q,h \rangle= \\ &= \underbrace{\| h \|^2}_{o(h)} + \underbrace{\| p+h-q_h \|^2 - \| p+h-q \|^2}_{\le 0} \le o(h), \end{aligned}\] co jest połową naszej tezy. Powyżej \(\| h \|^2\) jest ,,książkowym” przykładem wyrazu \(o(h),\) natomiast nierówność \(\| p+h-q \|^2 \geq \| p+h-q_h \|^2\) wynika z określenia punktu \(q_h.\) Z podobnych względów prawdziwa jest nierówność \(\| p-q_h \|^2 \ge \| p-q \|^2,\) która przyda się, jeśli skorzystamy z tej samej tożsamości, ale inaczej: \[\begin{gathered} (\ldots) = \underbrace{\| h \|^2}_{o(h)} + \underbrace{\| p-q_h \|^2 - \| p-q \|^2}_{\ge 0} + \underbrace{2 \langle h, q-q_h \rangle}_{o(h)} \ge o(h). \end{gathered}\] Tym razem pojawił się dodatkowy wyraz, ograniczony w module przez \(2 \| h \| \cdot \| q-q_h \|,\) a więc również postaci \(o(h).\) Okazuje się w ten sposób, że \(d_K^2(p+h) - d_K^2(p) - 2 \langle p-q,h \rangle\) jest szacowane z obu stron przez \(o(h),\) czyli samo jest wręcz postaci \(o(h).\) To kończy dowód różniczkowalności \(d_K^2\) w \(p.\)
W dowodzie korzystamy z tożsamości \(\| a+b \|^2 = \| a \|^2 + \| b \|^2 + 2 \langle a, b \rangle,\) która sprowadza się do znanego ze szkoły wzoru \((a+b)^2 = a^2+b^2+2ab.\) Obok stosujemy ją dla \(a = p-q\) i \(b = h,\) a w dalszej części dla \(a = p-q_h\) i \(b = h.\)
Zamiast zakończenia. W dowodzie Twierdzenia Motzkina było wiele zwrotów akcji, rozumowań nie wprost czy też trickowych obserwacji. Współczesna matematyka pełna jest podobnych rozumowań i dlatego też jest niezwykle ciekawa.
Hörmander, Lars, Notions of convexity. Progress in Mathematics, 127. Birkhäuser Boston, Inc., Boston, MA, 1994. viii+414 pp. ISBN: 0-8176-3799-0.