Afiliacja: Uniwersytet im. Adama Mickiewicza w Poznaniu
Jean d’Alembert (1717–1783), francuski filozof, matematyk i fizyk, wyraził opinię, że algebra jest szczodra – często daje więcej, niż jest o to proszona. Te słowa d’Alemberta nigdy nie przestały być aktualne – niejednokrotnie problemy matematyczne były (i nadal są) rozwiązywane przy użyciu algebry, nawet jeśli w samym sformułowaniu zagadnienia nie widać jej śladu.
Przez sferę potocznie rozumie się zbiór punktów przestrzeni trójwymiarowej równoodległych od zadanego punktu. Tak opisujemy sferę dwuwymiarową. Podobnie postąpimy przy określeniu sfery \((n-1)\)-wymiarowej w przestrzeni euklidesowej \(\mathbb{R}^n\) dla dowolnej liczby naturalnej \(n \geq 1.\) Przestrzeń ta składa się z punktów postaci \(x = (x_1, \dots, x_n)\); to jest \(n\)-tek liczb rzeczywistych, zwanych współrzędnymi punktu \(x.\) Punkt \(0 = (0, \dots, 0)\) nosi nazwę początku układu współrzędnych. Skupiając się na sferach jednostkowych, zbiór punktów \(x \in \mathbb{R}^n\) odległych o \(1\) od początku układu współrzędnych, to jest o normie \(\lVert x \rVert = 1,\) nazywamy sferą \((n-1)\)-wymiarową i oznaczamy przez \(\mathbb{S}^{n-1}.\) Przez normę punktu \(x\) rozumiemy liczbę \(\lVert x \rVert = \sqrt{x_1^2 + \ldots + x_n^2},\) która jest odległością punktu \(x\) od punktu \(0.\) Bohaterami tego artykułu są sfery \(\mathbb{S}^0\) (zbiór dwupunktowy \(\{ -1,+1 \}\)), \(\mathbb{S}^1\) (okrąg), \(\mathbb{S}^2\) (standardowa sfera), \(\mathbb{S}^3,\) \(\dots,\) niezmiennie przyciągające uwagę matematyków. Nim odpowiemy na pytanie zadane w tytule, omówimy własności, o których myślimy przy mnożeniu punktów na sferze. Najpierw jednak przyjrzymy się sferom \(\mathbb{S}^0,\) \(\mathbb{S}^1,\) \(\mathbb{S}^3\) oraz \(\mathbb{S}^7.\)
Sfery o wymiarach \(0\) i \(1.\)
\(\cdot\) \(1\) \(-1\) \(1\) \(1\) \(-1\) \(-1\) \(-1\) \(1\)
Tabelka określająca działanie mnożenia na sferze \(\mathbb{S}^0\)
Sfera \(\mathbb{S}^0\) to zbiór \(\{ -1, 1\},\) w którym liczby \(\pm 1\) mnożymy tak, jak nas uczono od dziecka (zob. tabelkę na marginesie). Sfera \(\mathbb{S}^1\) składa się z par \((x,y)\) liczb rzeczywistych spełniających \(x^2 + y^2 = 1,\) jest więc okręgiem o promieniu \(1.\) A jak mnożyć pary liczb rzeczywistych? Odpowiedzią jest zbiór liczb zespolonych oznaczany przez \(\mathbb{C},\) czyli zbiór \(\mathbb{R}^2\) z działaniami: \[c+z = (a+x,b+y), \ c \cdot z = (ax-by, ay+bx), \ \ \ c = (a,b), \ z = (x,y).\] Dodawanie wykonujemy po prostu na każdej współrzędnej z osobna, natomiast pewną motywację dla mnożenia można znaleźć na marginesie. Mnożenie takie jest przemienne, co oznacza tyle, że zawsze zachodzi \(c \cdot z = z\cdot c.\)
Działania \(+,\cdot\) na parach postaci \((x,0)\) są zgodne ze zwykłymi działaniami na (odpowiadających tym parom) liczbach rzeczywistych \(x,\) można je więc utożsamić. Przy tej konwencji jednostka urojona, to jest para \(i = (0,1),\) spełnia równanie \(i\cdot i = -1.\) Każdą parę \((x,y)\) można zapisać w postaci \(x+iy,\) wtedy formalne dodawanie i mnożenie takich wyrażeń (po przyjęciu \(i^2 = -1\)) prowadzi do działań, które właśnie określiliśmy.
Przydatne są pojęcia modułu \(|z| = \sqrt{x^2+y^2}\) i sprzężenia \(\overline{z} = (x,-y)\) liczby zespolonej \(z = (x,y) \in \mathbb{C}.\) Pozwalają one łatwo opisać element odwrotny (ze względu na mnożenie) do dowolnej liczby zespolonej \(z\neq (0,0)\): jest nim \({z^{-1} = \overline{z}/|z|^2}.\) Nietrudno się też przekonać, że \(|c \cdot z| = |c| \cdot |z|,\) więc w szczególności iloczyn dowolnych dwóch liczb z okręgu \(\mathbb{S}^1\) również leży na tym okręgu. W ten sposób uzyskujemy mnożenie punktów okręgu \(\mathbb{S}^1.\)
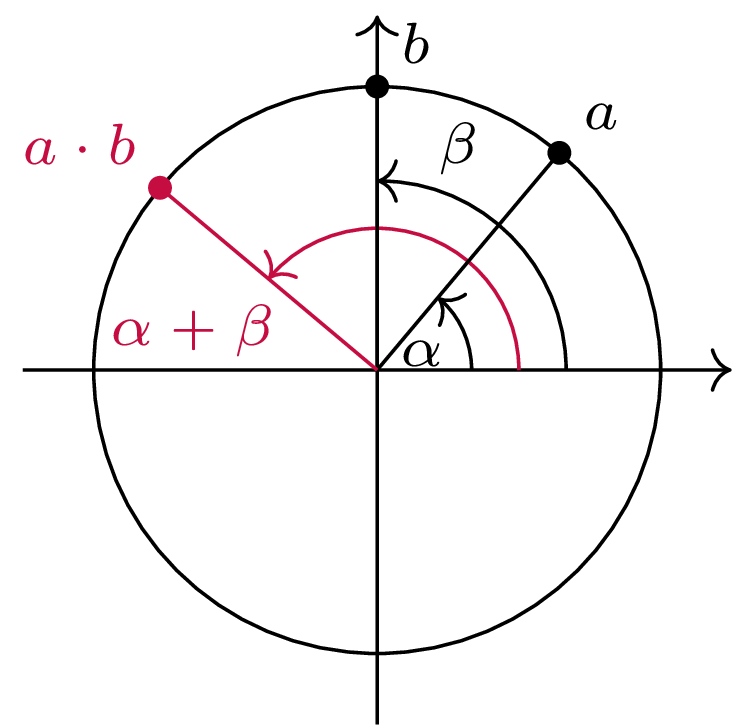
Geometryczna interpretacja mnożenia na okręgu \(\mathbb{S}^1\): iloczynem punktów \(a = (\cos \alpha, \sin \alpha)\) i \(b = (\cos \beta, \sin \beta)\) jest punkt \(a\cdot b = (\cos(\alpha+\beta), \sin(\alpha+\beta)),\) a więc mnożenie polega na dodaniu odpowiednich kątów z dokładnością do wielokrotności liczby \(2\pi\)
Sfery o wymiarach \(3\) i \(7.\)
William W. Hamilton, poszukując bezskutecznie wzoru na mnożenie trójek liczb rzeczywistych, znalazł (już przez nas podany) wzór na mnożenie par liczb rzeczywistych, po czym rozszerzył go na mnożenie par liczb zespolonych w następujący sposób: \[(a, b) \cdot (x,y) = (ax - \overline{y}b, ya + b\overline{x}).\] Tym razem symbol \(\cdot\) użyty jest w iloczynie \((a,b) \cdot (x,y)\) par liczb zespolonych. Dodawanie par określa się jak zwykle: \((a,b) + (x,y) = (a+x, b+y).\) Przy tych działaniach zbiór \(\mathbb{C}\times \mathbb{C}\) (tożsamy ze zbiorem czwórek liczb rzeczywistych, czyli \(\mathbb{R}^4\)) oznacza się przez \(\mathbb{H},\) a jego elementy nazywa się kwaternionami. Moduł i sprzężenie kwaternionu \(z = (x,y)\) o liczbach zespolonych \(x = (x_1, x_2)\) i \(y = (y_1,y_2)\) określone są wzorami: \[\begin{aligned} & |z| = \sqrt{|x|^2 + |y|^2} = \sqrt{x_1^2 + x_2^2 + y_1^2 + y_2^2}, \\ & \ \overline{z} = (\overline{x}, -y) = (x_1, -x_2, -y_1, -y_2), \end{aligned}\] a wzór \(z^{-1} = \overline{z}/ |z|^2\) określa element odwrotny (ze względu na mnożenie) do kwaternionu \(z\neq (0,0).\) Odnotujmy, że podobnie jak dla liczb zespolonych moduł iloczynu dwóch kwaternionów jest iloczynem ich modułów.
Sfera \(\mathbb{S}^3\) składa się z par \((x,y)\) liczb zespolonych spełniających \(|x|^2 + |y|^2 = 1,\) co oznacza, że \(x_1^2 + x_2^2 + y_1^2 + y_2^2 = 1\); inaczej mówiąc: sfera \(\mathbb{S}^3\) jest zbiorem kwaternionów o module \(1.\) Wzór na moduł iloczynu dwóch kwaternionów zapewnia, że iloczyn dwóch kwaternionów ze sfery \(\mathbb{S}^3\) również do niej należy – w ten sposób uzyskujemy mnożenie punktów ze sfery \(\mathbb{S}^3.\) Kwaterniony różni od liczb zespolonych jedna fundamentalna własność. Tym razem mnożenie nie jest przemienne: na przykład iloczyn \((0,1) \cdot (i,0)\) jest różny od \((i,0) \cdot (0,1).\)
W tekście Zbigniewa Marciniaka z \(\Delta^{10}_{16}\) można przeczytać więcej o kwaternionach, a nawet ogólnie o mnożeniu w przestrzeniach \(\mathbb{R}^2,\) \(\mathbb{R}^3\) i \(\mathbb{R}^4.\)
Czy procedurę tę można kontynuować? Odpowiedź brzmi: tak! Opierając się na konstrukcji zwanej metodą Cayleya–Dicksona, sumę i iloczyn dwóch par kwaternionów można określić tak samo, jak zrobił to Hamilton dla par liczb zespolonych (zob. margines). Po przyjęciu tych działań zbiór \(\mathbb{H}\times \mathbb{H}\) (tożsamy ze zbiorem \(\mathbb{R}^8\)) oznacza się przez \(\mathbb{O},\) a jego elementy nazywa oktonionami. Tak jak poprzednio, umożliwia to określenie mnożenia punktów ze sfery \(\mathbb{S}^7.\)
W 1843 roku William W. Hamilton (1805–1865) podał wzór na mnożenie kwaternionów, uznając je za pary liczb zespolonych. W tym samym roku, inspirowany odkryciem Hamiltona, John T. Graves (1806–1870) rozszerzył ten wzór na mnożenie par kwaternionów: \[(a,b) \cdot (x,y) = (a x - \overline{y} b, y a + b \overline{x}),\] a pary te nazwał oktawami. Natomiast my nazywamy je oktonionami.
Przyjmijmy oznaczenia na kwaterniony: \(\mathbf{1}= (1,0),\) \(\mathbf{i}= (i,0),\) \(\mathbf{j}= (0,1),\) \(\mathbf{k}= (0,i).\) Dla oktonionów \(p = (\mathbf{i},0),\) \(q = (0,\mathbf{j}),\) \(r = (0,\mathbf{1})\) iloczyn \((p \cdot q) \cdot r\) różni się od \(p \cdot (q \cdot r),\) gdyż pierwszy jest równy \((\mathbf{k},0),\) a drugi \((-\mathbf{k},0).\)
W jakimś stopniu mnożenie oktonionów jest jednak łączne, na przykład \(x \cdot (a\cdot b) \cdot x = (x \cdot a) \cdot (b \cdot x)\) oraz \((x \cdot y) \cdot y^{-1} = x\) dla wszystkich oktonionów \(a,\) \(b,\) \(x,\) \(y.\)
Tak określone działanie mnożenia oktonionów, podobnie jak mnożenie kwaternionów, nie jest przemienne, a na dodatek nie jest łączne, nawet wtedy, gdy ograniczymy się do oktonionów ze sfery \(\mathbb{S}^7\) (zob. przykład na marginesie).
Własności mnożenia.
Na każdej ze sfer \(\mathbb{S}^0,\) \(\mathbb{S}^1,\) \(\mathbb{S}^3\) określiliśmy działanie mnożenia. Pomyślmy, jakie są wspólne własności tych działań. Jak łatwo jest zauważyć, dla wszystkich punktów z danej sfery \(G\):
istnieje taki punkt \(e,\) że \(e \cdot x = x = x \cdot e\) dla każdego punktu \(x \in G\);
dla każdego \(x \in G\) istnieje taki punkt \(x^{-1},\) że \(x \cdot x^{-1} = e = x^{-1} \cdot x\);
\((x \cdot y) \cdot z = x \cdot (y \cdot z)\) dla dowolnych trzech punktów \(x, y, z.\)
W pierwszej własności rolę punktu \(e\) pełni jedynka (rzeczywista, zespolona lub kwaternionowa); punkt \(e\) nazywa się elementem neutralnym mnożenia. Druga własność jest spełniona dla \(x^{-1} = \overline{x}/ |x|^2.\) Trzecia własność nazywa się łącznością mnożenia. Mnożenie liczb rzeczywistych i zespolonych spełnia też własność (4): \(x \cdot y = y \cdot x,\) zwaną przemiennością mnożenia. Jak już odnotowaliśmy, mnożenie kwaternionów nie jest przemienne, a mnożenie oktonionów nie jest ani przemienne, ani łączne.
Definicja. Przez mnożenie grupowe w zbiorze \(G\) rozumie się taką funkcję \(\mu \colon G \times G \to G,\) że po oznaczeniu wartości \(\mu(x,y)\) symbolem \(x \cdot y\) spełnione są wymienione wyżej własności (1), (2), (3). Zbiór \(G\) z ustalonym mnożeniem grupowym nazywa się grupą. Jeżeli dodatkowo spełniona jest własność (4), to grupa \(G\) nazywa się grupą abelową.
Istnieje bardzo ważna własność natury topologicznej, którą posiada mnożenie na każdej ze sfer \(G = \mathbb{S}^0,\) \(\mathbb{S}^1,\) \(\mathbb{S}^3,\) \(\mathbb{S}^7.\) Otóż funkcja \(G \times G \to G,\) przypisująca parze \((x, y)\) element \(x \cdot y,\) jest ciągła. Również funkcja \(G \to G,\) zastępująca elementy \(x\) elementami odwrotnymi \(x^{-1}\!,\) jest ciągła. Wynika to z faktu, że działanie mnożenia liczb rzeczywistych jest ciągłe, oraz z postaci wzoru na mnożenie użytego w metodzie Cayleya–Dicksona, który (za każdym razem) gwarantuje ciągłość mnożenia.
Definicja. Zbiór \(G\) (zawarty w jakiejś przestrzeni euklidesowej) z ustalonym ciągłym mnożeniem grupowym \(G \times G \to G\) i ciągłą funkcją \(G \to G,\) zastępującą elementy ich odwrotnościami, nazywa się grupą topologiczną.
Podsumujmy: sfery \(\mathbb{S}^0,\) \(\mathbb{S}^1,\) \(\mathbb{S}^3\) są grupami topologicznymi (pierwsze dwie nawet abelowymi) z działaniami mnożenia, odpowiednio: liczb rzeczywistych, zespolonych i kwaterionów o module \(1.\) Mnożenie oktonionów o module \(1\) nie pozwala uznać sfery \(\mathbb{S}^7\) za grupę topologiczną, bo mnożenie to nie jest łączne. Co więcej, jak udowodnili Zhou Jian i Xu Senlin w 1988 roku, na sferze tej nie istnieje takie mnożenie grupowe: sfera \(\mathbb{S}^7\!\) nie jest grupą topologiczną.
Podkreślmy tutaj, że mówienie o ciągłości funkcji ma sens, gdy wprowadzimy pojęcie, które umożliwi nam ścisłe określenie tej intuicyjnie jasnej koncepcji. W naszym przypadku możemy się oprzeć na pojęciu odległości dwóch punktów w przestrzeni euklidesowej, gdyż jeśli grupa \(G\) zawiera się w przestrzeni \(\mathbb{R}^n,\) to produkt kartezjański \(G \times G\) zawiera się w przestrzeni \(\mathbb{R}^{2n}.\)
Odwzorowanie \(\mu \colon G \times G \to G\) nazwiemy jednostajnie ciągłym, jeżeli dla każdej liczby rzeczywistej \(\varepsilon> 0\) istnieje taka liczba rzeczywista \(\delta > 0,\) że dla dowolnych dwóch par \((a, x), (b, y) \in G \times G\) o odległości mniejszej niż \(\delta\) iloczyny \(a\cdot x\) oraz \(b \cdot y\) są w odległości mniejszej niż \(\varepsilon.\) Pojęcie ciągłości odwzorowania jest słabsze od jednostajnej ciągłości, lecz te dwa pojęcia się jednak pokrywają, jeśli ograniczymy się do podzbiorów domkniętych i ograniczonych w przestrzeni euklidesowej, czyli podzbiorów zwartych. Dodajmy jeszcze, że odległość pomiędzy dwoma punktami \(x\) i \(y\) w przestrzeni \(\mathbb{R}^n\) określona jest przez normę \(\lVert x - y \rVert\) z różnicy \(x - y = (x_1 - y_1, \dots, x_n - y_n)\).
Przypomnijmy, że sfery \(\mathbb{S}^0,\) \(\mathbb{S}^1,\) \(\mathbb{S}^3\) są grupami topologicznymi. Topologia algebraiczna dostarcza silnych metod matematycznych, które umożliwiają wykazanie, że w każdym innym przypadku, to jest dla \(n \neq 0, 1, 3, 7,\) na sferze \(\mathbb{S}^n\) nie istnieje ciągłe działanie grupowe. Wobec tego prawdziwe jest następujące twierdzenie:
Twierdzenie klasyfikacyjne. Sfery \(\mathbb{S}^0,\) \(\mathbb{S}^1\!\) i \(\mathbb{S}^3\) są jedynymi sferami, które posiadają strukturę grupy topologicznej.
Sfera dwuwymiarowa.
Na zakończenie wykażemy, że sfera \(\mathbb{S}^2,\) od której zaczęliśmy ten artykuł, nie może być grupą topologiczną. Potrzebne nam będzie pojęcie styczności wektora do sfery, które najłatwiej wprowadzić przy użyciu iloczynu skalarnego: \[\langle x, y\rangle = x_1y_1 + x_2y_2 + x_3y_3\] dla \(x= (x_1,x_2,x_3),\) \(y= (y_1,y_2,y_3).\)
Iloczyn skalarny pozwala wyrazić w sposób algebraiczny prostopadłość dwóch wektorów \(x\) i \(y\), o których (w sposób geometryczny) myślimy jak o strzałkach zaczepionych w punkcie \((0,0,0)\) i grotach (odpowiednio) w punktach \(x\) i \(y\). Powiemy, że wektory \(x\) i \(y\) są prostopadłe, jeżeli \(\langle x, y \rangle = 0\).
Za wektor styczny do sfery w punkcie \(x \in \mathbb{S}^2\) uznajemy dowolny wektor \(y \in \mathbb{R}^3\) prostopadły do wektora \(x,\) czyli spełniający równość \(\langle x, y \rangle = 0.\) Przykładowo w punkcie \((1,0,0)\) styczny jest każdy wektor postaci \((0,y_2,y_3).\) W ogólności, jeśli wektor \(y \in \mathbb{R}^3\) nie jest styczny w \(x \in \mathbb{S}^2,\) to jego składowa prostopadła do sfery w tym punkcie wyraża się wzorem \(\langle y, x \rangle x,\) a zatem rzut prostopadły punktu \(y\) na płaszczyznę styczną wynosi \(y - \langle y, x \rangle x.\)
Przez (ciągłe) pole styczne rozumiemy ciągłą funkcję \(\varphi\colon \mathbb{S}^2 \to \mathbb{R}^3,\) która każdemu punktowi \(x \in \mathbb{S}^2\) przyporządkowuje pewien wektor styczny w punkcie \(x.\) Innymi słowy, żądamy, by spełniona była tożsamość \(\langle \varphi(x), x \rangle = 0\) dla \(x \in \mathbb{S}^2.\) Przykłady takich pól stycznych można zobaczyć na marginesie, warto też stworzyć własne przykłady. Ich wspólną cechą jest istnienie miejsc zerowych, czyli takich punktów \(x \in \mathbb{S}^2,\) którym przyporządkowano wektor zerowy \((0,0,0).\) Twierdzenie Poincarégo mówi, że nie da się tego uniknąć:
\((x_1,x_2,x_3) \mapsto (-x_1x_3, -x_2x_3, 1-x_3^2)\) to pole ,,z południa na północ”
\((x_1,x_2,x_3) \mapsto (-x_2, x_1, 0)\) to pole ,,z zachodu na wschód”
Twierdzenie Poincarégo. Każde pole styczne \(\varphi\colon \mathbb{S}^2 \to \mathbb{R}^3\) posiada co najmniej jedno miejsce zerowe.
O twierdzeniu Poincarégo pisaliśmy już w \(\Delta^{5}_{97}\). Czytelnika zainteresowanego ogólnością może zaciekawić fakt, że podobne twierdzenie jest prawdziwe dla sfer \(\mathbb{S}^2,\mathbb{S}^4,\mathbb{S}^6,\ldots\) – pole styczne na każdej z nich posiada miejsce zerowe. Dobrym ćwiczeniem jest samodzielne przekonanie się, że wyklucza to istnienie struktury grupy topologicznej na tych sferach, zgodnie z rozumowaniem przedstawionym niżej.
Twierdzenie Poincarégo (znane także pod nazwą twierdzenia o zaczesaniu sfery) ma następujące popularnonaukowe ujęcie: Nie da się wybrać niezerowych wektorów stycznych do sfery \(\mathbb{S}^2\) we wszystkich jej punktach w ten sposób, by wybór zależał w sposób ciągły od punktów styczności. Jeszcze inaczej: Sfery porośniętej włosiem nie da się uczesać, czyli każdy włos położyć stycznie do sfery.
Dowód twierdzenia klasyfikacyjnego w przypadku \(n = 2\). Przypuśćmy, że na sferze \(\mathbb{S}^2\) istnieje ciągłe działanie grupowe z elementem neutralnym \(e \in \mathbb{S}^2.\) Skonstruujemy wówczas pole styczne pozbawione miejsc zerowych, co doprowadzi do sprzeczności z twierdzeniem Poincarégo.
Dla wybranego elementu \(a\in \mathbb{S}^2\) rozważmy przekształcenie zastępujące dowolny punkt \(x \in \mathbb{S}^2\) iloczynem \(a\cdot x,\) a następnie jego rzutem prostopadłym \(p_x(a \cdot x)\) na płaszczyznę styczną w punkcie \(x\). Daje to funkcję \[\varphi\colon \mathbb{S}^2 \to \mathbb{R}^3, \ \ \ \varphi(x) = p_x(a \cdot x) = a \cdot x - \langle a \cdot x, x \rangle x.%\] Funkcja ta jest jednostajnie ciągła, co wynika z jednostajnej ciągłości działania grupowego. Styczność \(\varphi(x)\) można też sprawdzić bezpośrednim rachunkiem: \(\langle \varphi(x), x \rangle = 0.\) Pozostaje więc wykluczyć istnienie miejsc zerowych \(\varphi,\) i w tym celu konieczne będzie uważne wybranie odpowiedniego elementu \(a.\)
Wektor \(\varphi(x)\) jest tym wektorem stycznym do sfery w \(x,\) który wskazuje w kierunku punktu \(a\cdot x\)
Kiedy więc zachodzi równość \(\varphi(x) = 0\)? Otóż wtedy, gdy wektor z \(x\) do \(a\cdot x\) jest prostopadły do sfery, a to zachodzi w dokładnie dwóch przypadkach: I) \(a\cdot x = x\) oraz II) \(a\cdot x = -x\) (zob. rysunek obok). Równość w przypadku I) sprowadza się do \(a = x \cdot x^{-1},\) czyli \(a = e.\) Łatwo jest więc ten przypadek wykluczyć – wystarczy dobrać \(a\neq e.\)
Trudniej jest z równością w II). Ponieważ sfera \(\mathbb{S}^2\) jest zwartym (czyli domkniętym i ograniczonym) podzbiorem przestrzeni euklidesowej \(\mathbb{R}^3,\) możemy skorzystać z jednostajnej ciągłości działania grupowego \(\mu \colon \mathbb{S}^2 \times \mathbb{S}^2 \to \mathbb{S}^2.\) W definicji przyjmijmy wartość liczby \(\delta > 0\) odpowiadającą \(\varepsilon= 2\) i odczytajmy, co warunek jednostajnej ciągłości oznacza dla par postaci \((e,x)\) i \((a,x).\) Odległość między tymi parami jest równa odległości od \(a\) do \(e\) (mierzonej w przestrzeni \(3\)-wymiarowej). Otrzymujemy więc, że jeśli odległość \(a\) od \(e\) jest mniejsza niż \(\delta,\) to odległość \(a\cdot x\) od \(e \cdot x,\) czyli od \(x,\) jest mniejsza niż \(2.\) To ostatnie stwierdzenie świadczy, że \(a\cdot x \neq -x,\) gdyż odległość \(-x\) od \(x\) jest równa \(2.\)
Wystarczy więc wziąć punkt \(a\in \mathbb{S}^2\) odległy od \(e \in \mathbb{S}^2\) o mniej niż \(\delta,\) a jednocześnie więcej niż zero. Dotychczasowe rozumowanie pokazuje, że wówczas pole styczne \(\varphi\) nie ma miejsc zerowych, a uzyskana sprzeczność z twierdzeniem Poincarégo dowodzi, że początkowe założenie o istnieniu ciągłych działań grupowych na \(\mathbb{S}^2\) było fałszywe. ◻