Afiliacja: Wydział Fizyki, Uniwersytet im. Adama Mickiewicza w Poznaniu
Ciągłe przejścia fazowe
Jeśli żelazny magnes podgrzejemy do temperatury powyżej 1043 K (\(770^\circ\)C), znanej jako temperatura Curie dla żelaza, to straci on swoje własności magnetyczne (namagnesowanie rozumiane jako suma wektorowa momentów magnetycznych pochodzących od wszystkich atomów żelaza). Można zaobserwować, że ta utrata namagnesowania następuje w ciągły sposób, w miarę jak temperatura żelaza zbliża się do temperatury Curie (\(T_C\)), nazywanej także temperaturą krytyczną. To zjawisko jest przykładem ciągłego przejścia fazowego. Takie przejścia fazowe zostały w bardzo przejrzysty sposób przedstawione w artykule Jacka Miękisza O spinach i genach \(\Delta^5_{15}\) – przed dalszą lekturą warto zapoznać się z częścią tego artykułu dotyczącą ,,spinów”.
Aby zrozumieć zjawisko utraty namagnesowania w temperaturze \(T_C,\) wprowadzono liczne modele magnetyków mające dwa istotne składniki: sieć (dla ustalenia uwagi przyjmijmy, że będzie to dwuwymiarowa sieć kwadratowa) oraz znajdujące się w jej węzłach momenty magnetyczne nazywane także spinami, z reguły oddziałujące tylko z momentami magnetycznymi z najbliższych węzłów. Najprostszy z nich to model Isinga: zakładamy, że momenty magnetyczne mogą być skierowane wyłącznie ,,w górę” albo ,,w dół” względem wybranego kierunku, a energia pary oddziałujących spinów skierowanych w jednym kierunku jest niższa od energii pary oddziałujących spinów skierowanych w różnych kierunkach. Stanem podstawowym (to jest stanem o najniższej możliwej energii, w temperaturze 0 K) takiego modelu jest więc stan, w którym wszystkie momenty magnetyczne zwrócone są w tym samym kierunku, a układ jako całość wykazuje maksymalne namagnesowanie.
Jeśli taki układ spinów będzie pobierał ciepło od otoczenia, to przypadkowe spiny będą zmieniały kierunek, energia będzie rosła, a namagnesowanie będzie spadało. Jednakże całkowicie zaskakującym faktem jest to, że w temperaturze krytycznej, \(T_C = 2,2692\) (liczonej w jednostkach \([\frac{\textup{J}}{k_{\textup{B}}}],\) J – dżul, \(k_{\textup{B}}\approx1{,}38\cdot10^{-23}\,\mathrm{J/K}\) – stała Boltzmanna), namagnesowanie staje się równe 0. Pokazano to na rysunku 1.
Rys. 1. Zależność namagnesowania, liczonego na jeden węzeł sieci, od temperatury dla dwuwymiarowego modelu Isinga [2]: \[m(T)=\left(1-\mbox{sinh}^{-4}\left(\frac{2}{T}\right)\right)^\frac{1}{8}\]
Mówimy także, że w temperaturze krytycznej \(T_C\) następuje spontaniczne złamanie symetrii: układ, aby ,,się uporządkować” poniżej \(T_C,\) łamie symetrię i spośród dwóch stanów o równej energii, lecz przeciwnym namagnesowaniu (,,góra” – ,,dół”) ,,wybiera” jeden.
Chcąc opisać ilościowo to zjawisko, definiuje się dwa parametry: namagnesowanie (zobacz artykuł O spinach i genach) oraz funkcję korelacji spin-spin: \[\Gamma (r)=\frac{\sum\sigma(0)\sigma(r)\exp\big(-\frac{E_i}{k_{\textup{B}}T}\big)}{\sum\exp\big(-\frac{E_i}{k_{\textup{B}}T}\big)}.\tag{1}\] \(\Gamma (r)\) to funkcja korelacji między spinami odległymi o \(r,\) sumowanie przebiega po wszystkich możliwych konfiguracjach (rozkładach) zmiennych spinowych \(\sigma,\) a \(E_i\) oznacza energię konkretnego rozkładu zmiennych spinowych.
Charakter zanikania funkcji korelacji z odległością między spinami jest różny w zależności od temperatury. I tak poniżej \(T_C\) funkcja korelacji maleje wolno z odległością \(r,\) zbiegając do \(m^2\) (kwadrat namagnesowania) dla \(r \rightarrow \infty.\) Konsekwencją takiego malenia funkcji korelacji poniżej \(T_C\) jest istnienie niezerowego namagnesowania poniżej \(T_C.\) W temperaturze dokładnie równej \(T_C\) oraz powyżej \(T_C\) dla \(r\to\infty\) mamy zanik \(\Gamma(r) \rightarrow 0,\) ale charakter zanikania funkcji korelacji w obu tych przypadkach jest różny – potęgowy w \(T_C\): \(\Gamma(r) \sim \frac{1}{r^{d-2+\eta}}\) (zanika bardzo wolno, \(\eta=\frac{1}{4}\) dla dwuwymiarowego modelu Isinga, \(d\)-wymiar), natomiast wykładniczy powyżej \(T_C\): \(\Gamma(r) \sim \exp (-r/\small \mbox{const}),\) zobacz rysunek 2.
Rys. 2. Funkcja korelacji \(\Gamma (r)\) w zależności od odległości \(r.\) Powyżej \(T_C\) (kolor niebieski) \(\Gamma(r)\) zanika wykładniczo, poniżej \(T_C\) (kolor zielony) \(\Gamma(r)\rightarrow m^2,\) a w \(T_C\) (kolor czerwony) \(\Gamma(r)\) zanika w sposób potęgowy
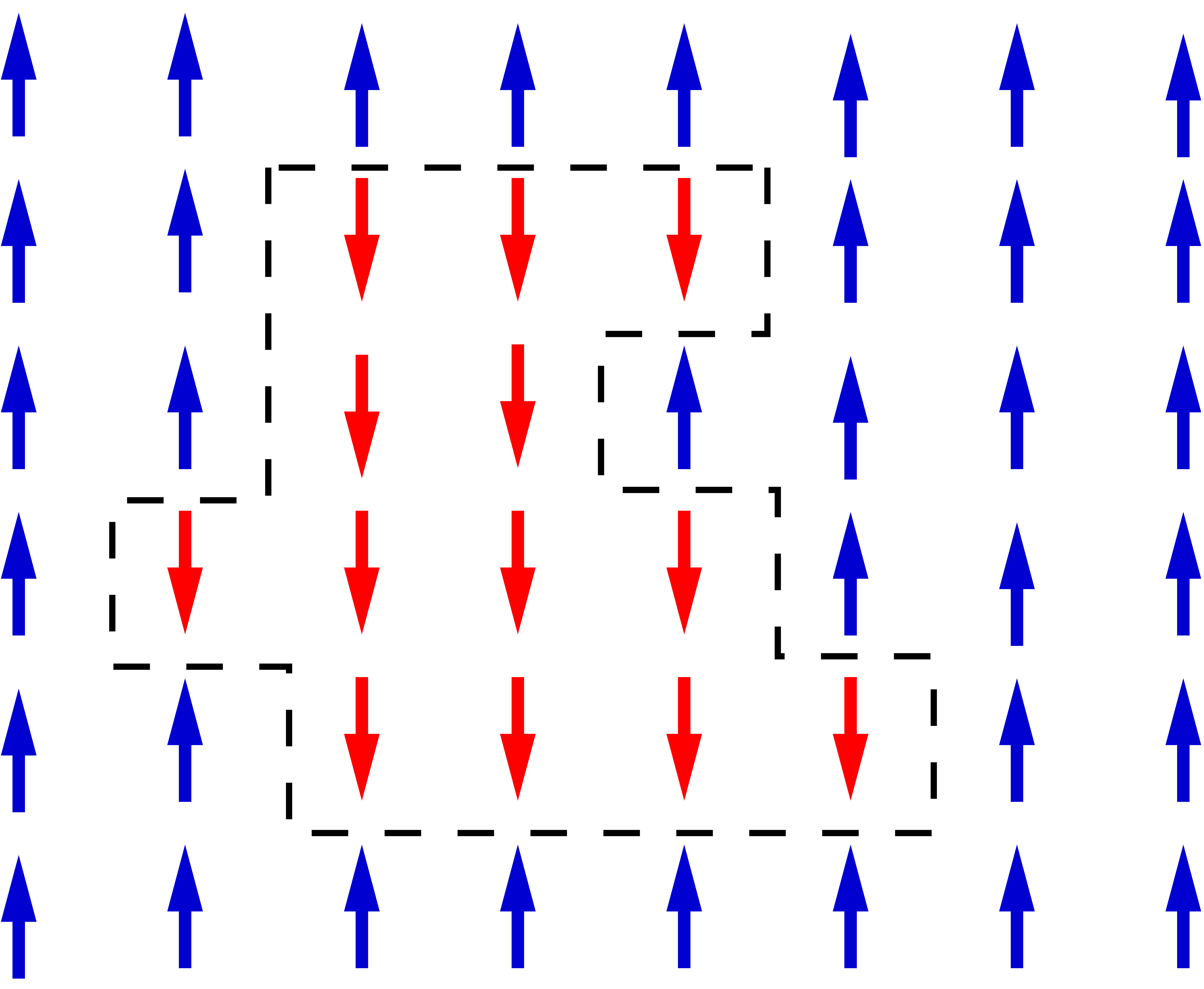
Istnienie niezerowej \(T_C\) wynika także w sposób niezbity z eleganckiego argumentu Peierlsa. Dla dwuwymiarowego modelu Isinga na sieci kwadratowej wygląda on następująco. Wyobraźmy sobie, że chcielibyśmy odwrócić wszystkie spiny z obszaru ograniczonego dużym wielokątem o obwodzie \(L\) (zobacz rys. 3). Związana z tym zmiana energii wewnętrznej \(U\) wynosi \(2LJ.\) Takie odwrócenie obszaru spinów ograniczonego wielokątem powoduje także zmianę entropii \(S\) układu, bo istnieje wiele możliwości wybrania zamkniętego wielokąta o długości \(L.\) Liczba tych możliwości jest równa w przybliżeniu \(3^L,\) dlatego że okrążając obszar ograniczony wielokątem, mamy do wyboru 3 niezależne kierunki w każdym węźle. W rzeczywistości, aby wielokąt zamknął się, ta liczba powinna być nieco mniejsza. Zmiana energii swobodnej \(\Delta F\) potrzebna do odwrócenia obszaru spinów wynosi więc \[\Delta F = \Delta U - T\Delta S = 2 L J - k_{\textup{B}} T \ln 3^L = L \left( 2 J - k_{\textup{B}} T \ln 3\right).\] Można zauważyć, że w wystarczająco wysokiej temperaturze, \(\frac{k_{\textup{B}} T}{J} =\frac{2}{\ln 3}\approx1{,}8205,\) odwrócenie obszaru spinów nie prowadzi do zmiany energii swobodnej, a więc może nastąpić samorzutnie. Takie samorzutne odwrócenie obszaru spinów to fluktuacja; fluktuacje w \(T_C\) powstają we wszystkich skalach długości (dla takiej temperatury zachodzi \(\Delta F=0\) niezależnie od \(L\)), to właśnie prowadzi do zerowego parametru porządku.
Rys. 3. Do odwrócenia momentów magnetycznych oznaczonych kolorem czerwonym i ograniczonych wielokątem o długości \(L=20\) potrzebna jest energia \(40J\)
Próbę zrozumienia przejścia fazowego w żelazie po raz pierwszy podjął Piotr Curie. Tę próbę określamy dzisiaj jako teorię pola średniego. Jej sformułowanie (1937) w postaci obecnie używanej pochodzi od Lwa Landaua. Postuluje ona istnienie parametru porządku, który ma niezerową wartość w fazie uporządkowanej i zerową w nieuporządkowanej. Ten sposób podejścia do opisu przejść fazowych jest podstawą ich zrozumienia od ponad 50 lat. Jednak, jak zaznaczono powyżej, bezpośrednim powodem istnienia niezerowego parametru porządku, co postulował Landau, był sposób zanikania funkcji korelacji poniżej \(T_C.\)
Ciągłe topologiczne przejścia fazowe
W połowie lat siedemdziesiątych ubiegłego wieku John M. Kosterlitz i David Thouless stwierdzili [3,4], że dla pewnego bardziej zaawansowanego modelu namagnesowania, zwanego modelem \(XY,\) funkcja korelacji w całym zakresie temperatur zanika w sposób potęgowy: \(\Gamma(r) \sim \big(\frac{1}{r}\big)^\frac{T}{2\pi},\) \(T\) liczona jest w jednostkach \([\frac{J}{k_{\textup{B}}}].\) Taka zależność oznacza brak porządku dalekozasięgowego. Zauważmy, że wykładnik określający malenie funkcji korelacji zależy od temperatury \(T.\)
Zasadnicza różnica między omówionym wcześniej modelem Isinga a modelem \(XY\) polega na tym, że kierunek momentu magnetycznego w każdym węźle sieci modelu \(XY\) może być scharakteryzowany przez kąt \(\theta_i\) z wybranym kierunkiem, zmieniający się w sposób ciągły od 0 do \(2\pi.\) Energia całego układu oddziałujących momentów magnetycznych wyniesie więc \[E = - J \sum_{\langle i,j\rangle} \cos(\theta_i-\theta_j).\] Sumowanie w powyższym wzorze przebiega po wszystkich \(N\) parach \(\langle i,j\rangle\) będących najbliższymi sąsiadami. Jeśli założymy, że kierunek momentu magnetycznego zmienia się nieznacznie od węzła do węzła, to możemy rozwinąć funkcję cosinus w szereg i pominąć wszystkie wyrazy tego rozwinięcia poza pierwszymi dwoma: \(\cos(\theta_i-\theta_j)\approx 1 - \frac{1}{2}(\theta_i-\theta_j)^2.\) W dalszym ciągu zakłada się, że rozkład momentów magnetycznych na sieci można przybliżyć przez ciągłe skalarne pole \(\theta(x,y),\) które zawiera informację, jak zmienia się kierunek momentu magnetycznego w zależności od współrzędnych. Wyrazy \((\theta_i-\theta_j)^2\) z rozwinięcia cosinusa w granicy ciągłego pola \(\theta(x,y)\) przybliża się kwadratem długości gradientu \(|\nabla \theta|^2.\) Energia pola \(\theta(x,y)\) dana jest wzorem: \[E = \frac{J}{2} \int |\nabla \theta|^2 \,dx \,dy \label{Energia},\tag{2}\] całkowanie odpowiada sumowaniu po najbliższych sąsiadach, a wyraz \(-NJ\) został pominięty. Wzór \(\eqref{Energia}\) może być także zrozumiany w taki sposób: w przypadku ,,wolnej” zmiany pola \(\theta(x,y)\) z odległością, zmiana jego energii powinna być skalarną funkcją jego gradientu \(\nabla \theta.\) Odpowiednim niezmiennikiem, który nie zależy od wyboru układu współrzędnych, zawierającym \(\nabla \theta\) dla skalarnego pola \(\theta\) okazuje się właśnie \(|\nabla \theta|^2.\)
Pole \(\theta(x,y)\) jest w stanie podstawowym (o najniższej energii), kiedy kierunek momentu magnetycznego nie zależy od współrzędnych. Wtedy gradient \(\nabla \theta\) pod całką równy jest 0. Trzy przykłady takich pól pokazano na rysunku 4. Zauważmy, że można narysować nieskończenie wiele takich przykładów, bo obrót wszystkich strzałek reprezentujących pole \(\theta(x,y)\) o ten sam kąt nie prowadzi do zmiany energii układu. W takiej sytuacji mówimy, że stan podstawowy takiego modelu ma nieskończoną degenerację.
Zgodnie z twierdzeniem Mermina–Wagnera taki układ nie wykazuje uporządkowania dalekozasięgowego w temperaturach poza bezwzględnym zerem. Jeśli będzie on pobierał ciepło od otoczenia, to jego temperatura będzie rosła, a dalekozasięgowy porządek obecny w stanie podstawowym zostanie zniszczony przez niezwykłe wzbudzenia. Mają one postać wirów albo antywirów (rys. 5), par wir-antywir (rys. 6).


Rys. 4. Trzy przykłady stanów podstawowych (o jednakowej energii – zdegenerowanych ze względu na energię) modelu \(XY\) dla stałych kątów \(\theta\) z prostą poziomą: od góry \(\theta= \frac{\pi}{3}, \frac{\pi}{4}, \frac{\pi}{6}\)

Rys. 5. Wysokotemperaturowe wzbudzenia topologiczne w modelu \(XY\): wir (z lewej), antywir (z prawej). Poglądowa interpretacja wzoru \(\eqref{ewir}\) jest następująca: przechodząc wzdłuż brzegu wiru w kierunku przeciwnym do ruchu wskazówek zegara, stwierdzamy, że czerwona strzałka obraca się o \(2\pi\) po pełnym okrążeniu wiru. W przypadku antywiru (po prawej) niebieska strzałka obraca się o \(-2\pi\) po jego pełnym okrążeniu przeciwnie do ruchu wskazówek zegara
Pary wir-antywir mogą wystąpić poniżej pewnej temperatury \(T_{KT},\) wiry i antywiry – powyżej tej temperatury. Między tymi typami wzbudzeń istnieje głęboka różnica natury topologicznej. Można ją scharakteryzować w następujący sposób. Jeśli wzbudzenie typu wir (albo antywir) otoczymy krzywą zamkniętą, którą obiegamy w kierunku przeciwnym do ruchu wskazówek zegara, i obliczymy po niej całkę krzywoliniową [5]: \[W = \oint \nabla \theta (x,y) \cdot d {\bf l}, \label{ewir}\tag{3}\] to wartość tej całki będzie zawsze różna od \(0\) – określony został w ten sposób winding number, który jest charakterystyką topologiczną dla wzbudzeń typu wir (lub antywir). Jeśli tę samą operację wykonamy dla par wir-antywir, to wynik całkowania będzie zawsze równy \(0.\) Wzbudzenia typu wir (antywir) różnią się więc topologicznie od wzbudzeń typu wir-antywir: jedne nie mogą być przekształcone w sposób ciągły w drugie. Z tego powodu omawiane przejście nazywane jest topologicznym przejściem fazowym, a temperaturę \(T_{KT},\) w której niszczone są pary wir-antywir i wzbudzenia przyjmują wyłącznie postać wirów (albo antywirów), nazywamy temperaturą krytyczną (Kosterlitza–Thoulessa). \(T_{KT}\) rozdziela więc dwie fazy: niskotemperaturową, w której wzbudzenie ma postać par wir-antywir (zobacz rys. 6), oraz wysokotemperaturową, w której wzbudzenia mają postać swobodnych wirów lub antywirów (zobacz rys. 5).
Rys. 6. Niskotemperaturowe wzbudzenie topologiczne w modelu \(XY\): para wir-antywir. Przechodząc wzdłuż brzegu w kierunku przeciwnym do ruchu wskazówek zegara, stwierdzamy, że niebieska strzałka obraca się po pełnym okrążeniu pary wir-antywir o kąt równy 0
Istnienie tego przejścia można także uzasadnić, odwołując się do argumentu Peierlsa. Należy więc, tak jak w przypadku modelu Isinga, oszacować wartość energii wzbudzenia (wiru) oraz zmianę entropii układu, która jest związana z jego powstaniem. Aby, stosując równanie \(\eqref{Energia}\), oszacować energię potrzebną do powstania jednego wiru na sieci o długości \(L\) i stałej sieciowej \(a,\) należy znać \(\nabla \theta.\) Z rysunku 5 można odczytać, że \(|\nabla \theta| \sim \frac{1}{r}.\) Oznacza to, że energia potrzebna do wykreowania jednego wiru wynosi (całka liczona jest we współrzędnych biegunowych): \[E_{wir} = \frac{J}{2} \int\nolimits_a^L \frac{1}{r^2} \,\, r \,dr \int\nolimits_0^{2\pi} \,d\phi = \pi J \ln \frac{L}{a}. \label{E_wir}\tag{4}\] Taki wir, jak widać na rysunku 5, można utworzyć w przybliżeniu na \(\bigl(\frac{L}{a}\bigr)^2\) sposobów. Związana z tym zmiana energii swobodnej wyniesie \[\Delta F = \pi J\log \frac{L}{a}-k_{\textup{B}}T\log\biggl(\biggl(\frac{L}{a}\biggr)^2\biggr).\tag{5}\] Stąd wynika, że dla \(\frac{k_{\textup{B}} T}{J} < \frac{\pi}{2}\) mamy \(\Delta F>0,\) i powstawanie wirów jest niekorzystne energetycznie. W tych temperaturach wzbudzenia będą miały postać par wir-antywir, które można w ciągły sposób przekształcić do stałego pola \(\theta(x,y),\) bo ich winding number równy jest 0. Jeśli natomiast \(\frac{k_{\textup{B}} T}{J} > \frac{\pi}{2},\) to \(\Delta F<0,\) wówczas powstawanie wirów jest korzystne energetycznie, a więc pary wir-antywir występujące w niższych temperaturach ulegają rozerwaniu i wiry oraz antywiry mogą istnieć samodzielnie.
Podsumowując, w modelu \(XY\) mamy brak uporządkowania magnetycznego dalekiego zasięgu w całym zakresie temperatur, ale w skończonej temperaturze \(T_{KT}\) występuje niezwykłe przejście fazowe. Polega ono na rozłączaniu par wir-antywir i powstawaniu nierównoważnych im topologicznie pojedynczych wirów i antywirów. Istotą tego przejścia jest zmiana topologii obiektów będących wzbudzeniami układu spinowego. Pięćdziesiąt lat po odkryciu topologicznych przejść fazowych, co zostało uhonorowane Nagrodą Nobla w 2016 roku, ten obszar jest wciąż przedmiotem intensywnych badań naukowych, nie tylko w kontekście prac eksperymentalnych, ale także zastosowania metod sztucznej inteligencji do rozpoznawania i klasyfikowania topologicznych faz materii [6].
Literatura:
[1] Jacek Miękisz, O spinach i genach, \(\Delta^{5}_{15}\)
[2] C.N. Yang, Phys. Rev. 85, 809 (1952).
[3] J.M. Kosterlitz, J. Phys. C: Solid State Phys. 7, 1046 (1974).
[4] J.M. Kosterlitz, D.J. Thouless, J. Phys. C: Solid State Phys. 6 1181 (1973).
[5] Por. wzór (1.4) i komentarz do niego w D.J Thoutess, Topological Quantum Numbers in Nonrelativistic Physics, World Scientific, 1998.
[6] Zob. np. J. Carrasquilla, R. Melko, Nature Physics 13, 431 (2017), E Lustig i in., Phys. Rev. Lett. 125, 127401 (2020).