Delta 5/2024

Zadania

Dominik Burek i Andrzej Majhofer

Zadanie M 1780

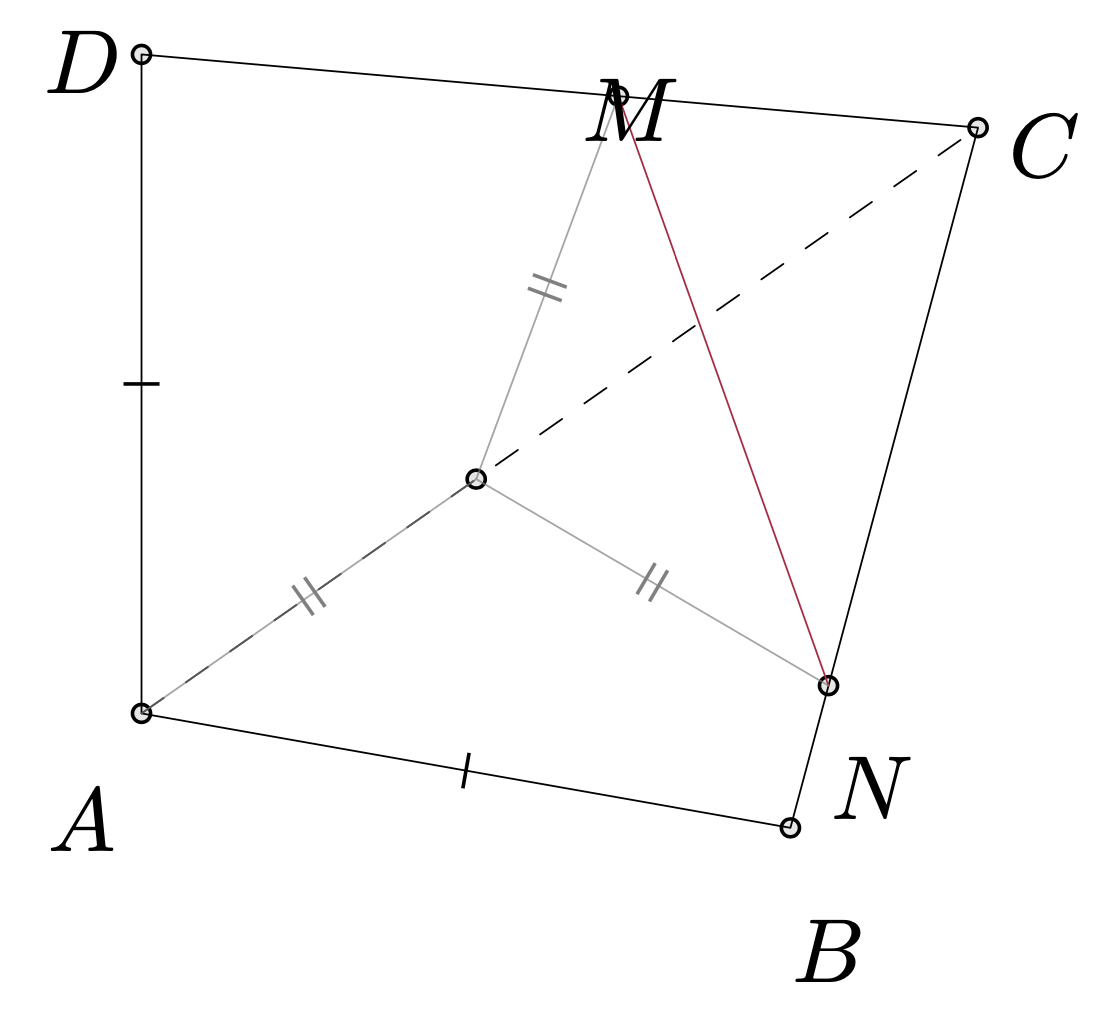
Czworokąt wypukły, w którym $AB=AD,$ jest wpisany w okrąg. Punkty $M$ i $N$ leżą na odcinkach $CD$ i $BC$ tak, że $DM+BN=MN.$ Udowodnić, że środek okręgu opisanego na trójkącie $AMN$ leży na odcinku $AC.$

Rozwiązanie

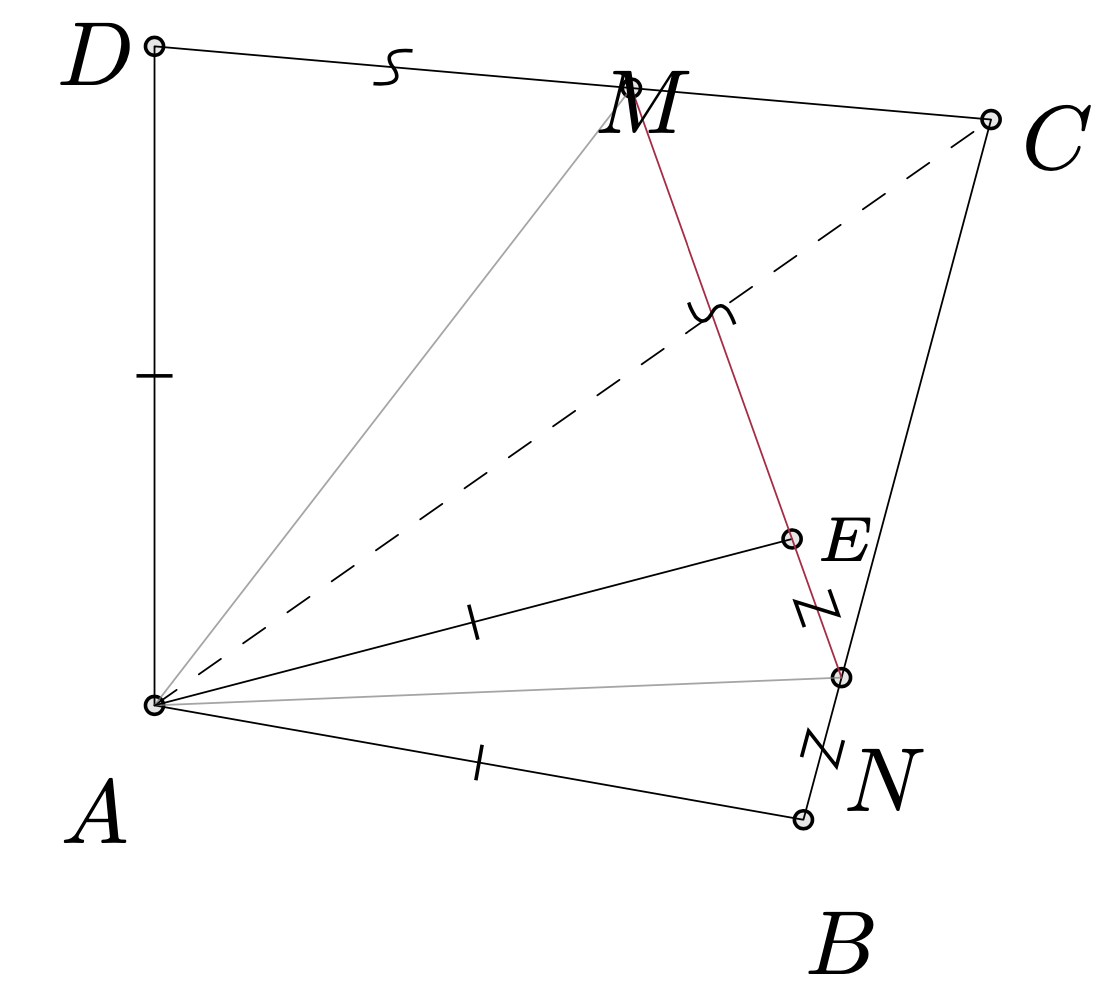
Zaznaczmy na odcinku $MN$ taki punkt $E,$ że $EM = MD.$ Wtedy $BN = NE.$ Wykorzystując równoramienność trójkątów $EDM$ i $EBN$ oraz równość $\measuredangle ABC+\measuredangle CDA=180^\circ=\measuredangle MEN,$ dostajemy \[\measuredangle ABE+\measuredangle ADE = \measuredangle AEB + \measuredangle AED.\] Gdyby $\measuredangle ABE > \measuredangle AEB,$ to $\measuredangle ADE < \measuredangle AED,$ skąd $AB < AE < AD,$ sprzeczność. Podobnie nie może zachodzić nierówność $\measuredangle ABE < \measuredangle AEB.$ Zatem $AB = AE = AD,$ więc pary trójkątów $ABN$ i $AEN$ oraz $AEM$ i $ADM$ są przystające. Wobec tego \[\begin{split} \measuredangle ANM +\measuredangle CAM&= \measuredangle ANB+\measuredangle CAM=\\ &=180^{\circ}-\measuredangle BAN-\measuredangle ABN+\measuredangle CAM=\\ &=180^{\circ}-\measuredangle BAN-\measuredangle ABD-\measuredangle MAD=\\ &=180^{\circ}-\frac{1}{2}\measuredangle BAD-\measuredangle ABD=90^\circ,\\ \end{split}\] co łatwo daje tezę zadania.

Zadanie M 1781

Znaleźć wszystkie liczby rzeczywiste dodatnie $x$ i $y$ takie, że \[2^{x^2+y}+2^{x+y^2}=128\ \ \ \textup{oraz}\ \ \ \sqrt{x}+\sqrt{y}=2\sqrt{2}.\]

Rozwiązanie

Po podniesieniu do kwadratu obu stron równości $\sqrt{x}+\sqrt{y}=2\sqrt{2}$ i wykorzystaniu nierówności $x+y\geq 2\sqrt{xy}$ dostajemy \[8 = x+y+2sqrt(xy) \le 2(x+y),\] skąd $x+y\geq 4.$ Ponadto z nierówności między średnią arytmetyczną a kwadratową mamy: \[\label{jej} x^2+y^2\geq \frac{1}{2}(x+y)^2,\tag{$*$}\] więc $x^{2}+y^{2}\geq 8.$ Ponownie korzystając z nierówności między średnią arytmetyczną a geometryczną, mamy: \[\begin{split} 64&=\frac{2^{x^2+y}+2^{x+y^2}}{2}\geq \sqrt{2^{x^2+y} \cdot 2^{x+y^2}}=\\&=2^{\frac{1}{2}(x^2+y+x+y^2)}\geq 2^{\frac{1}{2}(4+8)}=2^{6}=64. \end{split}\] Zatem $x+y=4$ oraz $x^2+y^2=8.$ Jednakże oznacza to, że w nierówności $\eqref{jej}$ mamy równość, stąd $x=y=2.$

Zadanie M 1782

Dane są liczby rzeczywiste $a>b$ takie, że $a^p-b^p$ jest liczbą całkowitą dla dowolnej liczby pierwszej $p.$ Udowodnić, że $a$ i $b$ są liczbami wymiernymi.

Rozwiązanie

Jeśli $ab=0$ lub $a+b=0,$ teza zadania jest jasna. Załóżmy więc, że $ab\neq 0$ i $a+b\neq 0.$ Z tożsamości \[\begin{gathered} (a^5-b^5)^2-(a^7-b^7)(a^3-b^3)=\\=a^3b^3(a^2-b^2)^2 \end{gathered}\] wynika, że $a^3b^3\in \mathbb{Q}.$ Z kolei z równości \[\begin{gathered} (a^7-b^7)^2-(a^{11}-b^{11})(a^3-b^3)=\\=a^3b^3(a^2-b^2)^2(a^2+b^2)^2 \end{gathered}\] wnioskujemy, że \[(a^2-b^2)^2+4a^2b^2=(a^2+b^2)^2\in \mathbb{Q},\] skąd $a^2b^2\in \mathbb{Q}.$ Zatem $ab=\frac{a^3b^3}{a^2b^2}\in \mathbb{Q}.$

Ponieważ \[\begin{gathered} (a^5-b^5)(a^{11}-b^{11})-(a^{13}-b^{13})(a^3-b^3)=\\=a^3b^3(a^2-b^2)^2(a^2+b^2)(a^4+b^4), \end{gathered}\] więc \[\begin{gathered} (a^3-b^3)^2+2a^3b^3+a^2b^2(a^2+b^2)=\\= (a^2+b^2)(a^4+b^4) \in \mathbb{Q}, \end{gathered}\] więc $a^2+b^2\in \mathbb{Q}.$ Finalnie \[a-b=\frac{a^3-b^3}{a^2+ab+b^2}\ \ \textup{oraz}\ \ a+b=\frac{a^2-b^2}{a-b}\] są wymierne, skąd $a$ i $b$ też są wymierne.

Uwaga: Można pokazać, że $a$ i $b$ są całkowite – pozostawiamy to jako ćwiczenie dla Czytelnika Wnikliwego.

Zadanie F 1095

W szczelnie zamkniętym naczyniu znajduje się $m = 54$ g pary wodnej w temperaturze $t_1 = 100$. Ile ciepła należy dostarczyć, aby ogrzać tę parę do $t_2 = 200$? Masa atomowa tlenu $\mu_O = 16,$ masa atomowa wodoru $\mu_H = 1,$ a uniwersalna stała gazowa $R = 8{,}314$ J/mol.

Rozwiązanie

Para wodna z dobrym przybliżeniem spełnia równanie gazu doskonałego. Cząsteczkę pary wodnej tworzą trzy (niewspółliniowe) atomy, a więc molowe ciepło właściwe pary ogrzewanej w stałej objętości $c_V = \frac{6}{2}R = 3R.$ Masa molowa wody $\mu_w = 2\mu_H + \mu_O = 18$ g. Ciepło potrzebne do ogrzania 54 g pary od $t_1 = 100$ do $t_2 = 200$ wynosi więc $Q = mc_V(T_2-t_1)/\mu_w$; liczbowo: $Q = 7{,}483\cdot 10^3$ J.

Zadanie F 1096

Ciało o masie $m$ porusza się wzdłuż linii prostej $OX$ pod działaniem siły potencjalnej. Potencjał siły jako funkcja współrzędnej $x$ opisany jest wzorem: \[U(x) = \frac{a}{x^2} - \frac{b}{x}.\] Jaki jest okres małych drgań ciała wokół położenia równowagi (minimum potencjału)?

Rozwiązanie

Położenie równowagi odpowiada minimum potencjału. Obliczmy pochodną $U(x)$ względem $x$ i przyrównajmy ją do zera, aby znaleźć współrzędną $x_0$ minimum. Mamy: \[U'(x) = -\frac{2a}{x^3} + \frac{b}{x^2} \longmapsto x_0 = \frac{2a}{b}.\] Siłę $F(x)$ działającą w punkcie $x$ otrzymamy jako $F(x) = - U'(x).$ Obliczmy jej wartość w punkcie bliskim minimum: $x = x_0 +z$: \[\begin{aligned} F(x_0 + z) &= \frac{2a}{(x_0+z)^3} - \frac{b}{(x_0 + z)^2} \approx\\& \approx U'(x_0) - U''(x_0)z. \end{aligned}\] Ponieważ interesują nas małe drgania, więc dokonaliśmy rozwinięcia siły do wyrazów liniowych w $z.$ Mamy $U'(x_0) = 0,$ a zatem otrzymujemy przybliżone równanie ruchu w pobliżu punktu równowagi ($x_0$): \[m\frac{d^2 z}{dt^2} = - \frac{b^4}{8a^3} z.\] Jest to równanie oscylatora harmonicznego o okresie: \[T = \frac{4\pi a}{b^2}\sqrt{2am}.\]