Klub 44

Oba warianty – odpowiedź tak. W podanych niżej przykładach przyjmujemy punkt $C$ za środek ustalonego okręgu $\mathrm{\Omega }$ (o dowolnym promieniu), na którym umieszczamy pozostałe cztery punkty:
(a) punkty $P,A,B,Q$ leżą na okręgu $\mathrm{\Omega }$ w tym porządku, w odległościach kątowych $\measuredangle PCA=\measuredangle ACB=\measuredangle BCQ={30}^{\circ }$;
(b) punkty $P,B,A,Q$ leżą na okręgu $\mathrm{\Omega }$ w tym porządku, w odległościach kątowych $\measuredangle PCB=\measuredangle ACQ={60}^{\circ },$ $\measuredangle BCA={150}^{\circ }.$

Czytelnikom zostawiamy przyjemność naszkicowania tych układów i przekonania się, że wskazane konfiguracje faktycznie spełniają postawione warunki.

[Ciekawostka: są to (w obu przypadkach) jedyne takie konfiguracje, z dokładnością do podobieństwa oraz cyklicznej permutacji symboli $A,B,C$].

Autor zadania, Piotr Kumor, proponuje rozwiązanie dla $r=4$ z użyciem liczb Fermata $F_n=2^{2^n}+1$ ($n=0,1,2,\dots$). Zaczniemy więc od przypomnienia niektórych ich własności (zapewne znanych Czytelnikom; krótkie uzasadnienia – dla kompletności):

1. $F_n=2+F_0{F}_1\dots F_{n-1}$    (banalna indukcja).

2. Liczby $F_n$ są parami względnie pierwsze (wniosek z W1).

3. Żadna z liczb $F_n$ nie jest potęgą liczby naturalnej o wykładniku większym od 1.

Uzasadnienie W3: przypuśćmy, że $F_n=a^t$ ($t>1$); jasne, że $t$ nie może być potęgą dwójki, więc ma dzielnik nieparzysty $s$; liczba $2^{2^n}=a^t-1$ dzieli się przez $a^s-1=(a-1)(a^{s-1}+\dots +a+1)$; to jednak niemożliwe, bo suma w drugim nawiasie jest nieparzysta.

Właściwe rozwiązanie opiera się na spostrzeżeniu, że aby uzyskać tezę dla $r=4,$ wystarczy wykazać, że dla nieskończenie wielu wykładników $w$ można znaleźć różne liczby pierwsze $p_1,p_2,p_3,p_4$ spełniające warunki: $$w\mid p_i-1,p_i\mid 2^w-1\text{dla}i=1,2,3,4.(\ast )$$ To faktycznie wystarczy, bowiem wówczas każda z liczb $2^{p_1-1}-1,\dots ,2^{p_4-1}-1$ dzieli się przez $2^w-1,$ więc też przez każdą z liczb $p_1,\dots ,p_4,$ więc i przez ich iloczyn.

Przydatna będzie kolejna, mniej banalna, własność liczb Fermata:

1. Jeśli $p\mid F_n$ ($p$ – liczba pierwsza; $n\ge 2$), to $2^{n+2}\mid p-1.$

Dowód.  Niech ${\delta }_n$ będzie najmniejszym wykładnikiem ($>1$), dla którego $2^{{\delta }_n}\equiv 1\text{ (mod }p).$ Ponieważ $2^{2^n}\equiv -1,$ zatem $2^{2^{n+1}}\equiv 1,$ co pokazuje, że ${\delta }_n=2^{n+1}.$ Także $2^{p-1}\equiv 1$ (małe tw. Fermata), więc ${\delta }_n\mid p-1,$ czyli $2^{n+1}\mid p-1.$ Skoro $n\ge 2,$ liczba $p$ ma postać $p=8m+1$ (dla pewnego naturalnego $m$). Ma więc miejsce przystawanie (mod $p$): $$\begin{array}{rl}(4m)!& =\prod _{k=1}^{2m}(2k)(1-2k)\equiv \\ & \equiv \prod _{k=1}^{2m}(2k)(8m+2-2k)=\prod _{k=1}^{4m}(2k)=2^{4m}(4m)!\end{array}$$ Uzyskaną kongruencję wolno podzielić przez $(4m)!$ ($\perp p$), otrzymując $2^{4m}\equiv 1.$ Tak więc ${\delta }_n\mid 4m,$ czyli $2^{n+1}\mid 4m,$ skąd $2^{n+2}\mid 8m.$ To kończy dowód własności W4 (znanej pod nazwą twierdzenie Lucasa).

Niech teraz $n$ będzie taką liczbą naturalną, że $F_n$ i $F_{n+1}$ są liczbami złożonymi. Z własności W2 i W3 wynika, że iloczyn $F_n{F}_{n+1}$ ma co najmniej cztery różne dzielniki pierwsze $p_1,p_2,p_3,p_4.$ Na mocy własności W4 każda z liczb $p_i-1$ dzieli się przez $2^{n+2}.$ Biorąc $w=2^{n+2},$ mamy (dla $i=1,2,3,4$) pierwszą podzielność $(\ast ).$ Druga też zachodzi, bowiem $2^w-1=F_{n+2}-2=F_0{F}_1\dots F_{n+1}$ (własność W1), a ten iloczyn dzieli się przez $F_n{F}_{n+1},$ więc i przez te cztery liczby pierwsze. (Warto zauważyć, że są one większe niż $2^{n+2}$).

Jeżeli istnieje nieskończenie wiele liczb $n,$ dla których $F_n$ i $F_{n+1}$ są liczbami złożonymi, to – zgodnie z akapitem otaczającym warunki $(\ast )$ – dostajemy obiecaną tezę dla $r=4.$

Jednak nikt nie wie, czy jest nieskończenie wiele takich par. Przyjmijmy więc, że nie; czyli że istnieje taka liczba $M,$ że dla każdego $n>M$ co najmniej jedna z liczb $F_n,$ $F_{n+1}$ jest liczbą pierwszą. Można przyjąć, że $M\ge 3,$ wtedy $2^n\ge n+9$ dla $n>M.$ Ustalmy taki numer $n.$ Wśród dziewięciu liczb $F_n,\dots ,F_{n+8}$ są co najmniej cztery liczby pierwsze $p_1,p_2,p_3,p_4.$ Ponownie sprawdzimy warunek $(\ast ),$ biorąc tym razem $w=2^{n+9}.$ Każda z czterech liczb $p_i$ jest pewną liczbą $F_{n+j}$ ($0\le j\le 8$), zatem $p_i-1=2^{2^{n+j}}$ dzieli się przez $2^{n+9},$ czyli przez $w.$

To pierwsza podzielność $(\ast ).$ Drugą uzasadniamy podobnie jak poprzednio: $2^w-1=F_{n+9}-2=F_0{F}_1\dots F_{n+8}$ (własność W1), a ten iloczyn dzieli się przez te cztery liczby pierwsze. Mogą one być dowolnie wielkie, skoro $M$ może być dowolnie wielkie.

To ostatecznie kończy dowód tezy dla $r=4$: istnieją czwórki dowolnie wielkich liczb pierwszych o wymaganych w zadaniu własnościach.

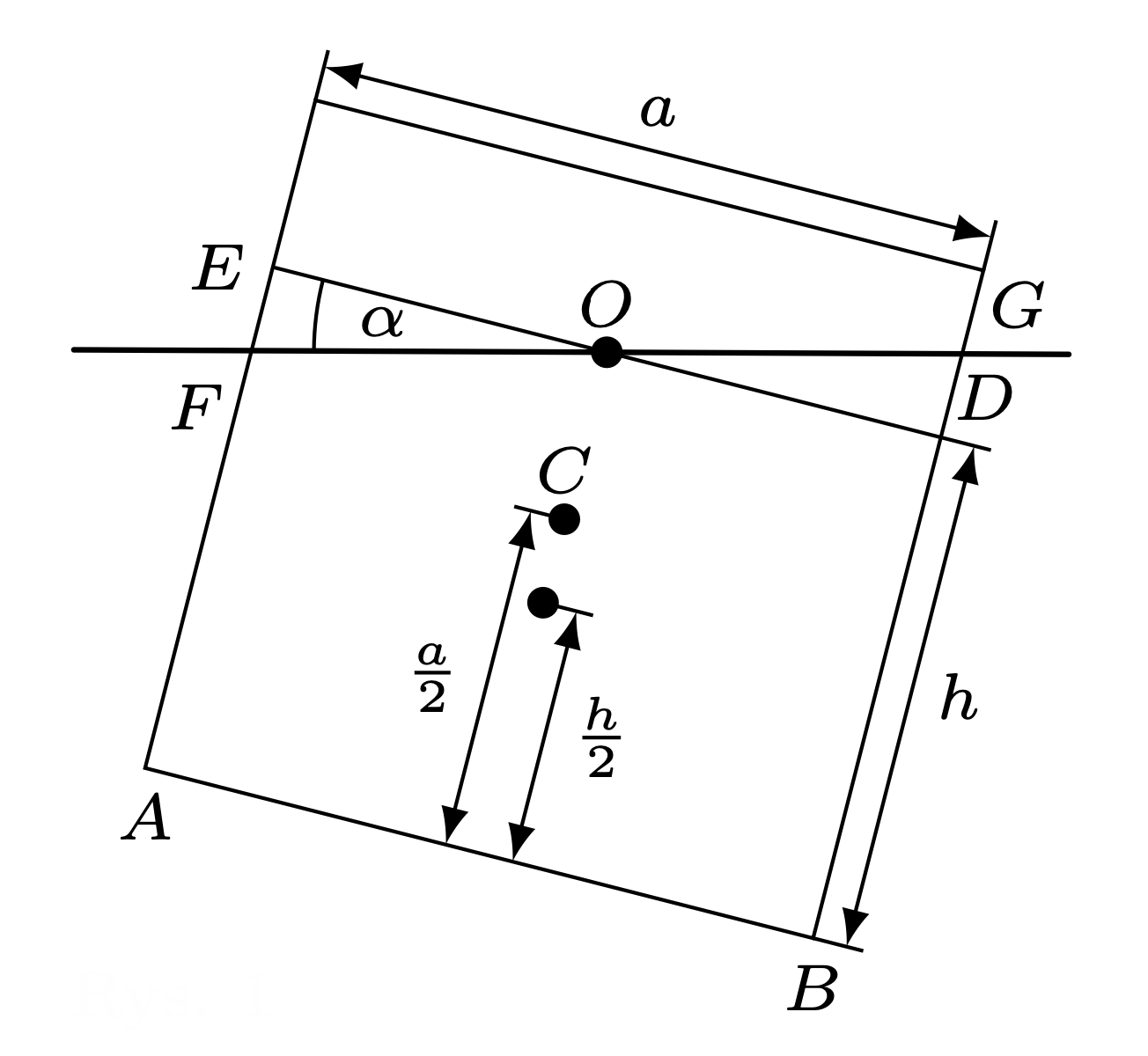
Klocek będzie pływał w stanie równowagi trwałej, gdy po obróceniu go o niewielki kąt $\alpha$ (rys. 1) wypadkowy moment sił będzie powodował jego powrót do położenia równowagi.

Rys. 1

Wygodnie jest liczyć momenty sił względem podłużnej osi klocka przechodzącej przez środek jego przekroju poprzecznego $C$ (rys. 1), bo względem tej osi moment siły ciężkości wynosi zero.

Moment siły wyporu działającej na część klocka zanurzoną w wodzie jest równy $$M=M_{OGD}-(M_{ABDE}-M_{OEF}).$$ Oznaczając: $M_{OGD}=M_{OEF}=M_2,$ $M_{ABDE}=M_1,$ możemy zapisać warunek na trwałość równowagi pływającego klocka: $$\begin{array}{}\text{(1)}& M>0\Rightarrow 2M_2>M_1.\end{array}$$ Oznaczając długość klocka przez $L,$ a gęstość wody przez $\rho ,$ mamy: $$\begin{array}{}\text{(2)}& M_1=\rho gLah{l}_1,\text{ gdzie }{l}_1=(a/2-h/2)\sin \alpha \approx (a/2-h/2)\alpha ,\end{array}$$ $$\begin{array}{}\text{(3)}& M_2=\rho gL{a}^2\mathrm{t}\mathrm{g}\alpha l_2/8\approx \rho gL{a}^2\alpha l_2/8,\text{ gdzie }{l}_2\approx 2a/6+(h-a/2)\alpha .\end{array}$$ Głębokość $h$ zanurzenia klocka w stanie równowagi znajdujemy z warunku $$\rho ahL={\rho }_x{a}^{2}L,\text{ gdzie }{\rho }_x\text{ jest gęstością klocka.}$$ Po podstawieniu $\text{(2)}$ i $\text{(3)}$ do $\text{(1)}$ i wprowadzeniu oznaczenia ${\rho }_x/\rho =x$ dostajemy: $$x^2-(1-\alpha /2)x+(2-3\alpha )/12>0.$$ Uwzględniając, że $\alpha$ jest małe, a $\rho =1$ g/cm${}^3$, otrzymujemy warunki na gęstość klocka: $$0<{\rho }_x<0,21\mathrm{g}/{\mathrm{c}\mathrm{m}}^3\text{ lub }0,79{\mathrm{g}/\mathrm{c}\mathrm{m}}^3<{\rho }_x<1\mathrm{g}/\mathrm{c}{\mathrm{m}}^3.$$

Aby w gumowej taśmie mogła rozchodzić się sprężysta fala poprzeczna, taśma musi być naciągnięta. W naszym zadaniu siła naciągu taśmy wywołana jest przez jej ruch obrotowy.

Rys. 2

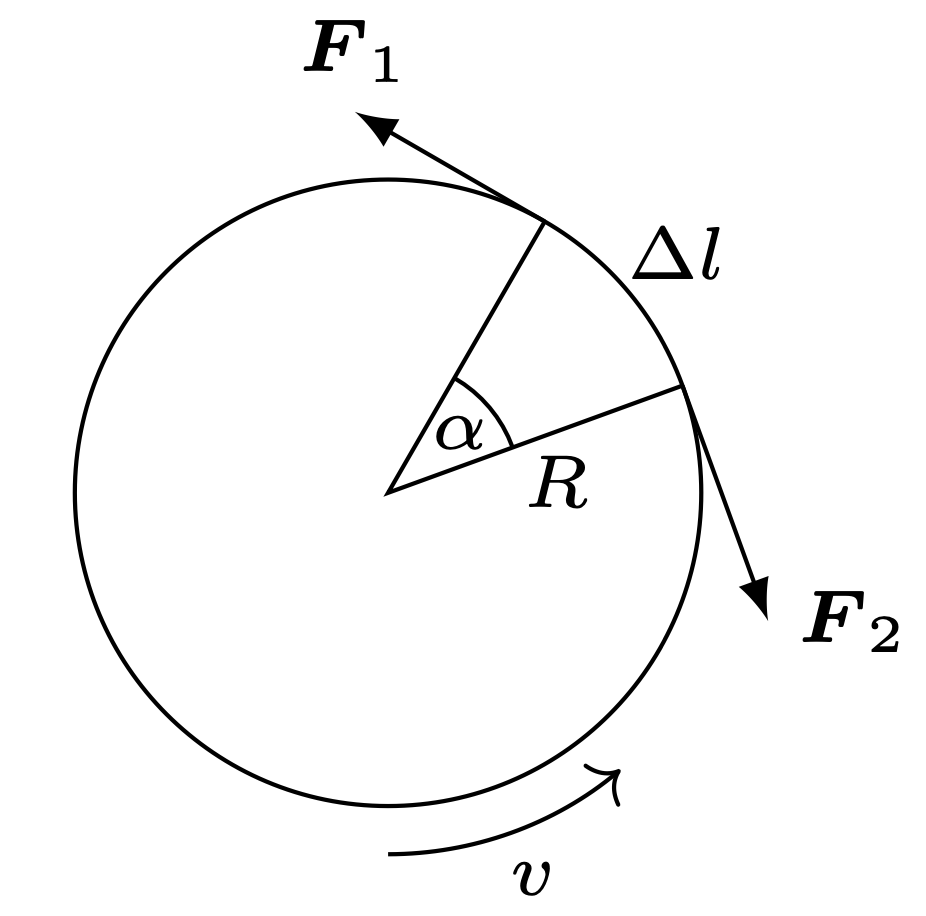
Rozważmy mały element taśmy o długości $\mathrm{\Delta }l=R\alpha$ i masie $\mathrm{\Delta }m=\rho S\mathrm{\Delta }l$ (rys. 2), gdzie $\rho$ jest jego gęstością a $S$ polem przekroju poprzecznego. Działają na niego sąsiednie elementy siłami ${\mathit{F}}_1$ i ${\mathit{F}}_2,$ stycznymi do taśmy. Wartość $F$ tych sił jest szukanym naciągiem taśmy, a ich wypadkowa nadaje rozważanemu elementowi przyspieszenie dośrodkowe $v^2/R.$ Zgodnie z drugą zasadą dynamiki $$F\alpha =\rho SR\alpha v^2/R,$$ stąd $$\begin{array}{}\text{(4)}& F=\rho S{v}^2.\end{array}$$ Szukana prędkość fali jest taka sama jak w przypadku prostoliniowej taśmy, której naciąg $F$ został uzyskany za pomocą sił zewnętrznych.

W inercjalnym układzie odniesienia poruszającym się wzdłuż taśmy z prędkością fali $u$ fala jest nieruchomą sinusoidą, a taśma ślizga się wzdłuż tej sinusoidy w kierunku przeciwnym do kierunku rozchodzenia się fali. Fragment trajektorii małego odcinka taśmy w pobliżu wierzchołka sinusoidy można przybliżyć przez łuk okręgu o promieniu $r$ oparty na kącie $\phi .$ Ponieważ amplituda drgań jest mała, możemy napisać: $$\begin{array}{}\text{(5)}& F\phi =\rho Sr\phi u^2/r,\text{ stąd }{u}^2=F/\rho S.\end{array}$$ Podstawiając wartość $F$ z $\text{(4)}$, otrzymujemy, że prędkość rozchodzenia się fali względem pierścienia równa jest prędkości obrotu pierścienia: $u=v.$