Delta 7/2024

Zadania

Dominik Burek i Andrzej Majhofer

Zadanie M 1786

W pola kwadratu \(11 \times 11\) wpisano parzystą liczbę plusów. Okazało się, że każdy kwadrat \(2\times 2\) również ma parzystą liczbę plusów. Udowodnić, że liczba plusów wpisanych w główną przekątną kwadratu też jest parzysta.

Rozwiązanie

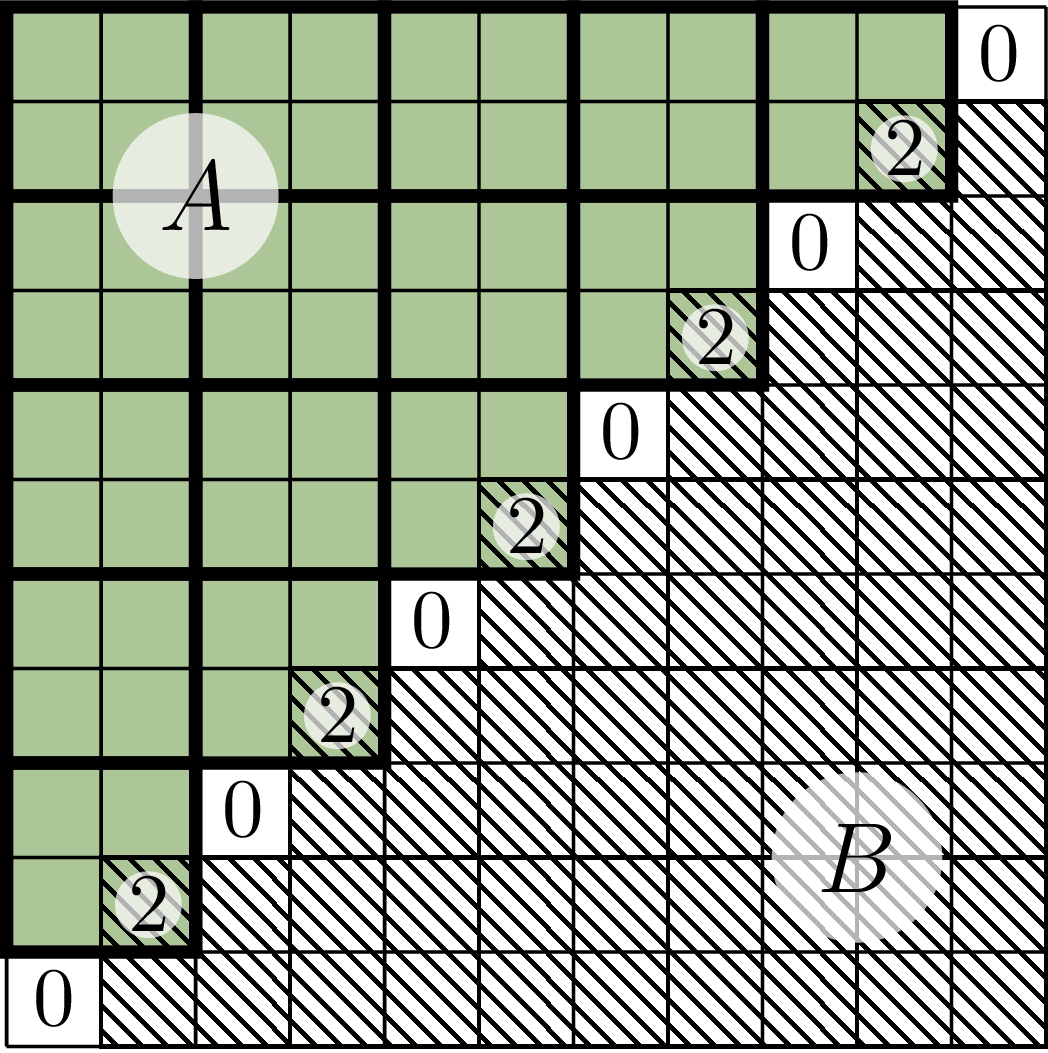
Figura \(A\) w lewym górnym rogu kwadratu (na rysunku oznaczona kolorem) składa się z \(15\) kwadratów \(2\times 2,\) a więc ma parzystą liczbę plusów. To samo dotyczy figury \(B,\) która jest symetryczna do figury \(A\) względem środka kwadratu. Każde pole kwadratu poza przekątną zakrywa dokładnie jedna z figur \(A\) i \(B,\) a każde pole przekątnej zakrywają obie lub żadna z nich. Ponieważ sumarycznie figury \(A\) i \(B\) mają parzystą liczbę plusów, przy czym plusy na polach z liczbą 2 są liczone dwukrotnie, więc liczba plusów poza przekątną jest parzysta. Ponieważ całkowita liczba plusów jest parzysta, liczba plusów na przekątnej również jest parzysta.

Zadanie M 1787

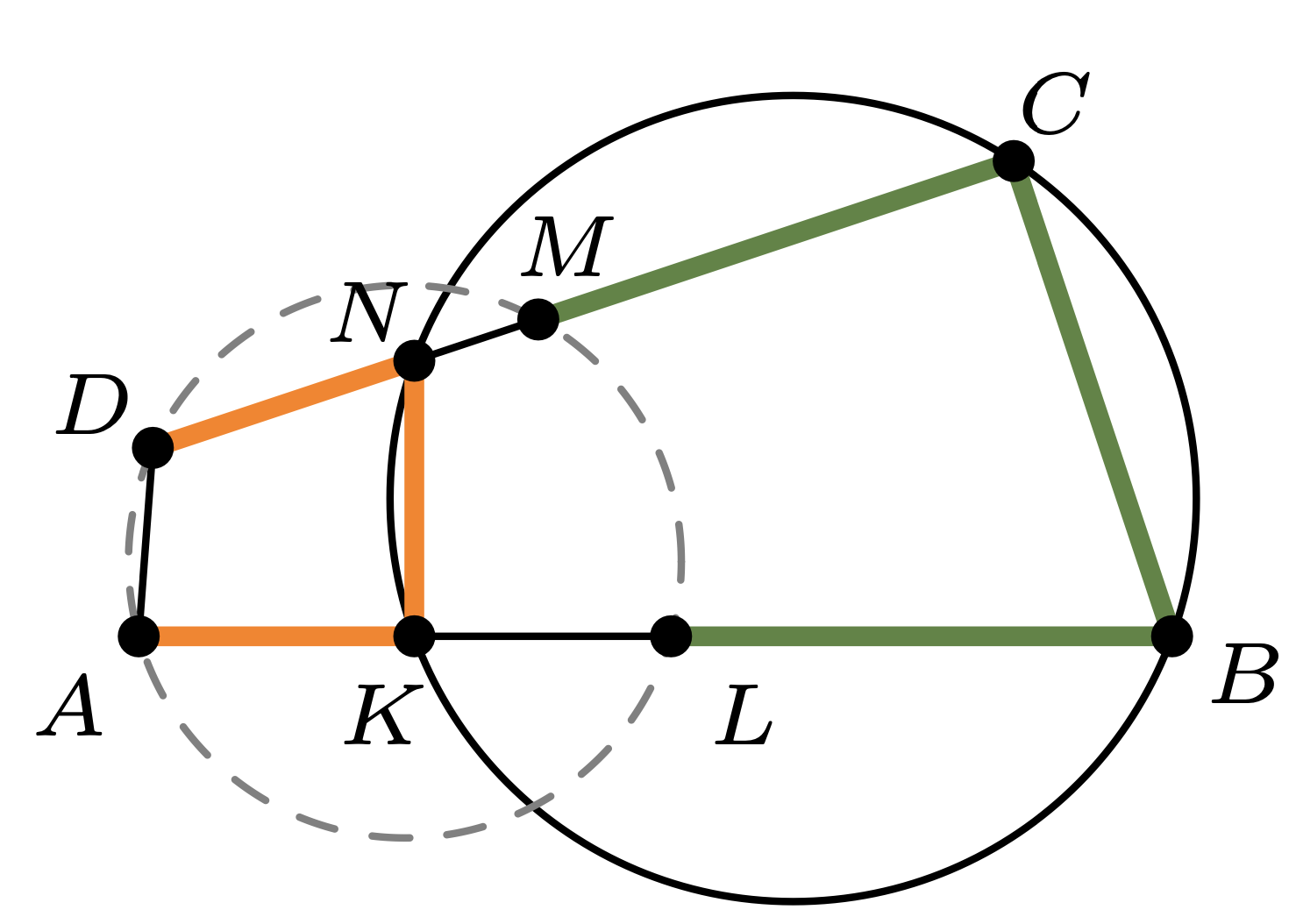
Punkty \(K\) i \(L\) leżą na boku \(AB\) czworokąta wypukłego \(ABCD\) (punkt \(K\) leży między \(A\) i \(L\)), a punkty \(M\) i \(N\) leżą na boku \(CD\) (punkt \(M\) leży między \(C\) i \(N).\) Wiadomo, że \(AK = KN = DN\) i \(BL = BC = CM.\) Udowodnić, że jeśli na czworokącie \(BCNK\) można opisać okrąg, to na czworokącie \(ADML\) również.

Rozwiązanie

Jeśli \(AB \parallel CD,\) to \(BCNK\) jest trapezem wpisanym w okrąg, zatem \(BC = KN\) oraz \(AK = BL = CM = DN.\) Oznacza to, że czworokąt \(LMDA\) otrzymujemy z \(BCNK\) poprzez równoległe przesunięcie o wektor \(\overrightarrow{BL}.\)

Załóżmy teraz, że \(AB\) i \(CD\) nie są równoległe; oznaczmy przez \(P\) punkt przecięcia prostych \(AB\) i \(CD.\)

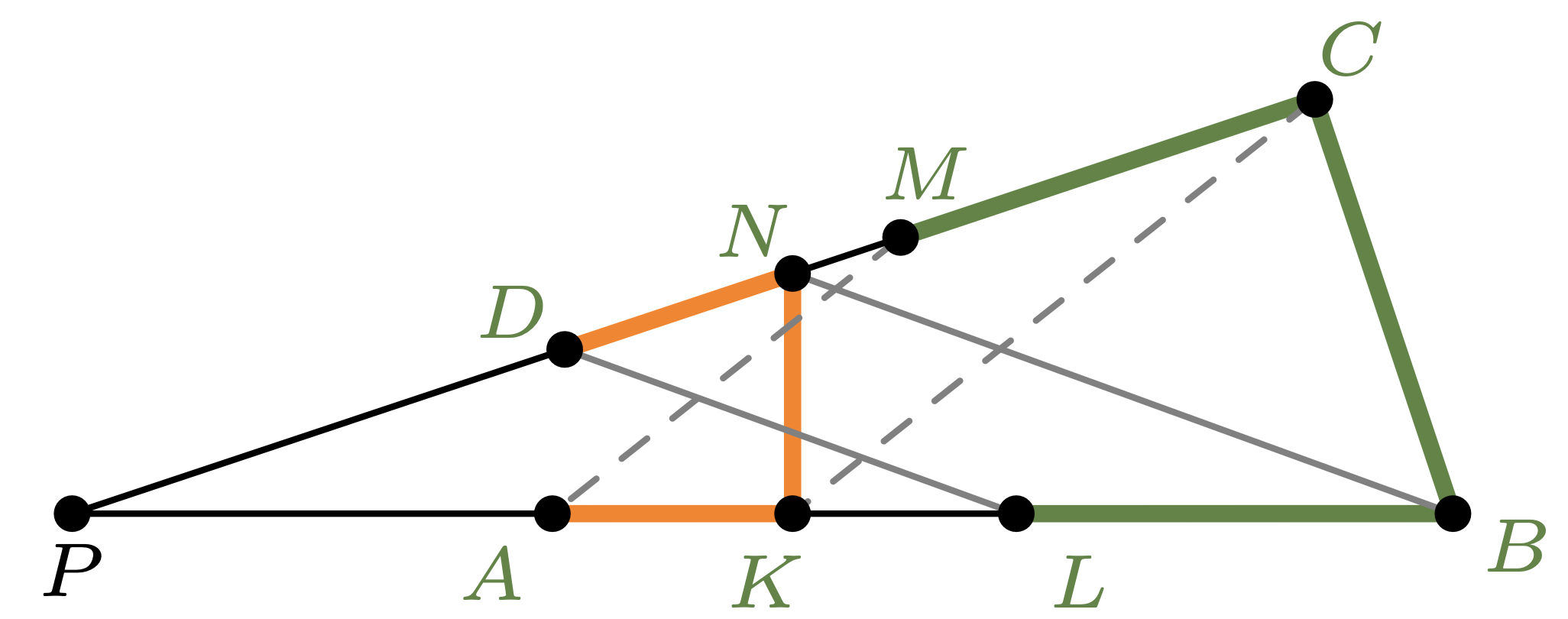
Ponieważ czworokąt \(BCNK\) jest wpisany w okrąg, to trójkąty \(PBC\) i \(PNK\) są podobne, zatem \[\frac{PB}{BL}=\frac{PB}{BC}=\frac{PN}{NK}=\frac{PN}{ND}.\] Dlatego \(BN \parallel LD,\) podobnie \(CK \parallel MA.\) Stąd otrzymujemy \(\measuredangle ALD = \measuredangle KBN\) i \(\measuredangle KCN = \measuredangle AMD.\)

Ponieważ na czworokącie \(BCNK\) można opisać okrąg, to \(\measuredangle KBN =\measuredangle KCN.\) Dlatego też \(\measuredangle ALD = \measuredangle AMD,\) czyli na czworokącie \(ADML\) również można opisać okrąg.

Zadanie M 1788

Ciąg liczbowy \(\{a_{n}\}_{n\geq 1}\) jest zdefiniowany następująco: \(a_{1}=1,\) \(a_{2}=2,\) \(a_{3}=3,\) \(a_{4}=4,\) \(a_{5}=5\) oraz \(a_{n+1}=a_{1}a_{2}\ldots a_{n}-1\) dla \(n\geq 5.\) Udowodnić, że \[a_{1}^2+a_{2}^2+\ldots + a_{70}^2=a_{1}a_{2}\ldots a_{70}.\]

Rozwiązanie

Wprowadźmy oznaczenie: \[b_{n}=a_{1}a_{2}\ldots a_{n}-(a_{1}^2+a_{2}^2+\ldots + a_{n}^2).\] Wystarczy udowodnić, że \(b_{70}=0.\) Zauważmy, że dla \(n\geq 5\) mamy \[\begin{split} b_{n+1}&=a_{1}a_{2}\ldots a_{n+1}-(a_{1}^2+\ldots + a_{n+1}^2)=\\ &=a_{1}a_{2}\ldots a_{n}(a_{1}a_{2}\ldots a_{n}-1)-\\ &\ \ \ -a_{1}^2-a_{2}^2+\ldots -a_{n}^2-\\ &\ \ \ -(a_{1}a_{2}\ldots a_{n}-1)^2=\\ &=a_{1}a_{2}\ldots a_{n}-a_{1}^2-a_{2}^2-\ldots - a_{n}^2-1=\\ &=b_{n}-1. \end{split}\] Ponadto \[\begin{aligned} b_{5}&=1\cdot 2\cdot 3\cdot 4\cdot 5-1^2-2^2-3^2-4^2-5^2=\\&=65, \end{aligned}\] zatem \(b_{6}=64, b_{7}=63, \ldots, b_{70}=0.\)

Zadanie F 1099

Oszacuj rozmiary cząsteczki azotu i odległości międzycząsteczkowe w gazowym azocie w warunkach normalnych (\(p = 1{,}013\cdot 10^5\) Pa, \(T = 0\)). Gęstość ciekłego azotu (w temperaturze wrzenia, \(-196\)) \(\rho_l = 0{,}808\) g/cm\(^3,\) gęstość azotu w warunkach normalnych \(\rho_g = 1{,}250\) g/l, liczba Avogadro \(N_A = 6{,}022\cdot 10^{23}\)/mol, liczba masowa atomu azotu \(A_N = 14.\)

Rozwiązanie

Gęstości tej samej substancji w stanie ciekłym i w stanie gazowym są niemal równe. Na potrzeby oszacowania możemy więc przyjąć, że w cieczy cząsteczki niemal się stykają. Masa jednego mola cząsteczek azotu wynosi \(\mu_N = 2A_N~\text{g} = 28\) g. Objętość jednego mola ciekłego azotu \(V = \mu_N/\rho_l\) (cząsteczki azotu są dwuatomowe). Objętość przypadająca na jedną cząsteczkę wynosi \(v= V/N_A,\) co odpowiada sześcianowi o boku \(d^3,\) gdzie \(d\) oznacza średnie rozmiary cząsteczki. Otrzymujemy: \[d = \left(\frac{\mu_N}{N_A\rho_l}\right)^{1/3}\!.\] Liczbowo \(d \approx 3{,}86\cdot 10^{-10}\) m. W stanie gazowym objętość przypadająca na jedną cząsteczkę wynosi \(\rho_l/\rho_g\) i jest około 650 razy większa niż w cieczy. Wynika stąd, że w gazie średnia odległość \(l\) między cząsteczkami azotu wynosi: \[l = \left(\frac{\rho_g}{\rho_l}\right)^{1/3} d \approx 8{,}65\ d.\] Liczbowo \(l \approx 33{,}4\cdot 10^{-10}\) m.

Zadanie F 1100

Ile razy energia wiązania cząsteczki azotu w polu grawitacyjnym Ziemi jest większa od średniej energii kinetycznej cząsteczek azotu w powietrzu? Przyjmij, że temperatura powietrza \(T = 300\) K, stała Boltzmanna \({k = 1{,}38\cdot 10^{-23}}\) J/K, przyspieszenie ziemskie \(g = 9{,}81\) m/s\(^2,\) promień Ziemi \(R = 6370\) km, liczba masowa atomu azotu \(A_N = 14,\) liczba Avogadro \({N_A = 6{,}022\cdot 10^{23}}\)/mol.

Rozwiązanie

Masa cząsteczki azotu wynosi \(m_N = (2A_N/N_A\)) g. Energia wiązania takiej cząsteczki przez pole grawitacyjne Ziemi wynosi (\(G\) to stała grawitacyjna, \(M\) to masa Ziemi): \[E_g = -\frac{GMm_N}{R} = -m_NgR.\] Średnia energia kinetyczna ruchu cieplnego wynosi \(E_k = 3kT/2.\) Stosunek tych energii wynosi: \[\left|\frac{E_g}{E_k}\right|= \frac{2m_NgR}{3kT}.\] Liczbowo \(|E_g/E_k| \approx 468.\) Energia kinetyczna ruchu cieplnego odpowiada pracy potrzebnej do podniesienia cząsteczki azotu na wysokość \(h\) nad powierzchnią Ziemi: \[h = \frac{3kT}{2gm_N}.\] Liczbowo \(h \approx 13{,}6\) km.