Errata do wersji w druku: Na dole strony 4 pojawia się zdanie „Jeśli takich permutacji jest dokładnie \(n!,\) to o grafie \(G\) mówimy, że jest asymetryczny” , które powinno brzmieć: „Jeśli tylko permutacja identycznościowa prowadzi do grafu izomorficznego z grafem \(G\), to mówimy, że jest on asymetryczny”,
Afiliacja: Politechnika Lubelska
Dużo. A nawet nieskończenie wiele! Taka odpowiedź nie jest zbyt ciekawa, więc spróbujmy zadać pytanie bardziej konkretne. Może: ile jest grafów o \(n\) wierzchołkach? W tym przypadku odpowiedź nie jest być może zupełnie oczywista, ale ciągle mało interesująca. Różnych par wierzchołków jest tyle samo co wszystkich dwuelementowych podzbiorów zbioru \(n\)-elementowego, czyli \(\binom{n}{2}\). Ponieważ każda taka para może być lub nie być połączona krawędzią, więc grafów jest \(2^{\binom{n}{2}}\). Mamy jednak świadomość, że pewne z tych grafów są w zasadzie identyczne – różnią się tylko etykietami, które nadaliśmy wierzchołkom. Na przykład dla \(n = 4\) grafy
Przez graf rozumiemy parę uporządkowaną \((V,E)\), w której \(V\) jest ustalonym zbiorem wierzchołków, a \(E\) zbiorem krawędzi traktowanym jako pewien podzbiór zbioru \(\lbrace{ \lbrace{ v,w \rbrace}: v,w \in V,\ v \neq w \rbrace}\). Krawędź \(\lbrace{ v,w \rbrace}\) będziemy dla uproszczenia oznaczać jako \(vw\).
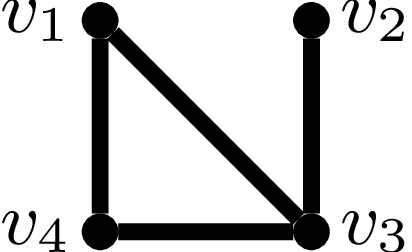
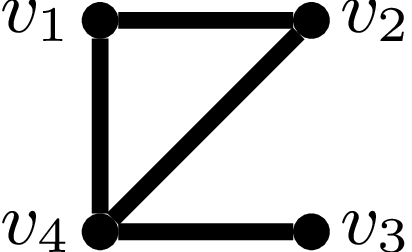
mają inne zbiory krawędzi, ale tak naprawdę są jednakowe. Wystarczy bowiem w pierwszym grafie zmienić numerację wierzchołków: \(v_1 \to v_2\), \(v_2 \to v_3\), \(v_3 \to v_4\), \(v_4 \to v_1\). Takich grafów nie chcemy zliczać osobno.
Powinniśmy w jakiś sposób utożsamić grafy, które różnią się wyłącznie nazwami wierzchołków. Powiemy, że dwa grafy \(G = (V,E)\) i \(G' = (V',E')\) są izomorficzne, jeżeli istnieje taka bijekcja \(f\colon V \to V'\), że \[vw \in E \ \ \ \text{wtedy i~tylko wtedy, gdy} \ \ \ f(v)f(w) \in E'\] dla dowolnych \(v,w \in V\). Intuicyjnie, dwa grafy są izomorficzne wtedy i tylko wtedy, gdy da się je narysować w ten sam sposób.
W rozważanym przykładzie ten izomorfizm już znaleźliśmy: \(f(v_1) = v_2\), \(f(v_2) = v_3\), \(f(v_3) = v_4\), \(f(v_4) = v_1\).
Możemy teraz zapytać:
Ile jest nieizomorficznych grafów o \(n\) wierzchołkach?
Dla \(n = 1\) taki graf jest tylko jeden i nie
ma żadnych krawędzi:

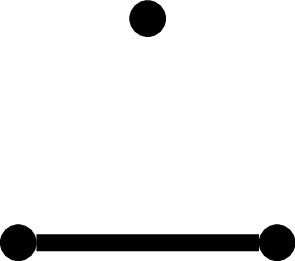
W przypadku \({n = 2}\) istnieją dwa różne grafy:
 i
i
 a dla \(n = 3\) cztery:
a dla \(n = 3\) cztery:

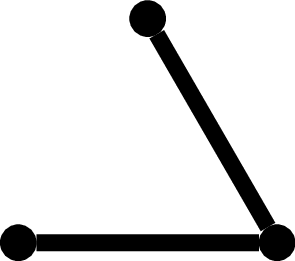
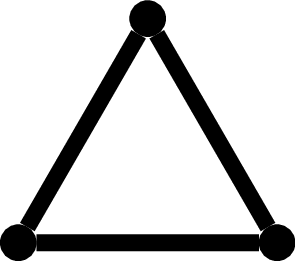
Trochę trudniej wyznaczyć wszystkie nieizomorficzne grafy zbudowane na czterech wierzchołkach, ale po paru minutach znajdziemy je wszystkie:
Samo narysowanie tych grafów to jedno, ale trzeba jeszcze pokazać, że żadne dwa z nich nie są izomorficzne oraz że żadnego nie brakuje.


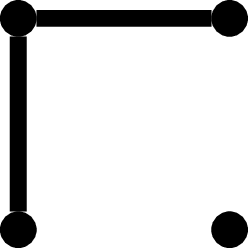
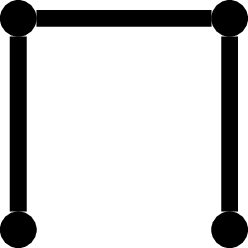



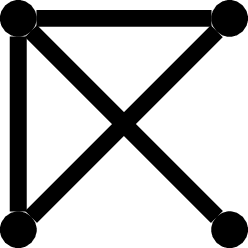


Oznaczając liczbę nieizomorficznych grafów o \(n\) wierzchołkach przez \(G_n\), sprawdziliśmy, że \(G_1 = 1\), \(G_2 = 2\), \(G_3 = 4\) oraz \(G_4 = 11\). Dla większych wartości \(n\) znalezienie \(G_n\) staje się coraz trudniejsze, nawet przy pomocy metod komputerowych. Powodem jest to, że nie znamy żadnego szybkiego (działającego w czasie wielomianowym) algorytmu, który sprawdzałby, czy dwa zadane grafy są izomorficzne.
Problem izomorficzności grafów należy do klasy NP (dla danej funkcji \(f\) łatwo sprawdzić, czy jest ona izomorfizmem), ale nie wiadomo, czy jest NP-zupełny ani czy należy on do klasy P. Wprowadzenie do klas złożoności Czytelnik znajdzie w artykule W. Czerwińskiego Dlaczego problem P = NP jest tak trudny? \((\Delta_{17}^3)\).
Możemy jednak stosunkowo łatwo oszacować liczbę \(G_n\). Ograniczeniem górnym jest oczywiście \(2^{\binom{n}{2}}\), ale domyślamy się, że nie jest to wartość optymalna. Spróbujmy znaleźć sensowne ograniczenie dolne. Zastanówmy się, ile grafów może być izomorficznych z danym grafem \(G.\) Z każdym takim izomorficznym grafem związana jest dowodząca izomorficzności permutacja wierzchołków \(G,\) więc grafów izomorficznych z \(G\) jest co najwyżej tyle, ile permutacji jego wierzchołków, czyli \(n!.\) ( Jeśli tylko permutacja identycznościowa prowadzi do grafu izomorficznego z grafem \(G\), to mówimy, że jest on asymetryczny – wtedy każde przeetykietowanie jego wierzchołków daje w efekcie inny graf). Skoro wszystkich grafów jest \(2^{{n\choose 2}},\) to z dokładnością do izomorfizmu jest ich co najmniej \(2^{{n\choose 2}}/n!.\) Ostatecznie \[\frac{2^{\binom{n}{2}}}{n!} \le G_n \le 2^{\binom{n}{2}}.\]
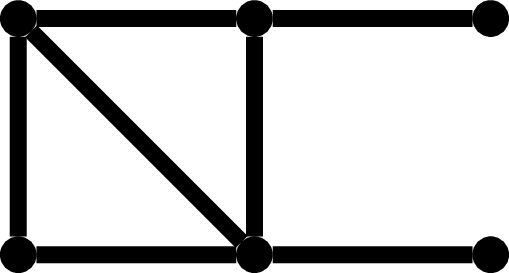
Każdy graf asymetryczny ma co najmniej sześć wierzchołków. Przykład poniżej.
Zwróćmy uwagę, że gdyby wszystkie grafy były asymetryczne, to nierówność z lewej strony stałaby się równością. Wiemy, że tak nie jest, bo dla każdego \(n\) istnieją grafy o \(n\) wierzchołkach, które nie są asymetryczne (na przykład grafy pełne, czyli kliki), Jeżeli jednak wyznaczymy, przy pomocy komputera, wartość \(G_n\) dla małych \(n\), to okaże się, że uzyskane dolne oszacowanie wcale nie jest takie złe.
W trzecim wierszu podaliśmy wartości \(2^{\binom{n}{2}}/n!\) zaokrąglone w górę. Dużym zaskoczeniem wydaje się fakt, że to oszacowanie jest coraz lepsze wraz ze wzrostem \(n\) i asymptotycznie okazuje się optymalne. Mówi o tym piękne i głębokie twierdzenie udowodnione przez Paula Erdősa, Alfréda Rényiego i George’a Pólyę. Wykazali oni, że prawie wszystkie grafy są asymetryczne, to znaczy przy \(n\) dążącym do nieskończoności stosunek liczby grafów asymetrycznych o \(n\) wierzchołkach do liczby wszystkich grafów o \(n\) wierzchołkach dąży do jednego, co implikuje poniższe twierdzenie.
Erdős i Rényi wykazali, iż prawdopodobieństwo zdarzenia, że losowo wybrany graf o \(n\) wierzchołkach jest asymetryczny, dąży do jedności przy \(n \to +\infty\), a Pólya znalazł asymptotykę \(G_n\).
Twierdzenie 1 (Erdős-Rényi-Pólya, 1963 r.). Mamy \[\lim_{n \to +\infty} \frac{G_n}{2^{\binom{n}{2}}/n!} = 1.\]
Na tym moglibyśmy właściwie zakończyć, ale prawdziwy skarb ciągle na nas czeka. Przejdźmy bowiem do grafów o przeliczalnej liczbie wierzchołków. Oczywiście nieizomorficznych grafów tego typu jest nieskończenie wiele, ale nas interesuje raczej to, jaką frakcję stanowią one w zbiorze wszystkich grafów. Aby to pytanie uściślić, wprowadźmy pojęcie grafu losowego.
Badanie grafów losowych zapoczątkowali wspomniani Erdős i Rényi.
Niech \(V = \lbrace{ v_i\colon i \in \mathbb N \rbrace}\) będzie ustalonym zbiorem wierzchołków. Ustawiamy w ciąg rodzinę wszystkich podzbiorów dwuelementowych \(\lbrace{ v_i, v_j \rbrace}\), \(i \neq j\) zbioru \(V\) i dla każdego z nich rzucamy symetryczną monetą. Jeżeli wypadł orzeł, to do zbioru krawędzi \(E\) dodajemy krawędź \(v_i v_j\). Tak skonstruowany graf \(G = (V,E)\) będziemy nazywać grafem losowym. Możemy teraz pytać, jakie jest prawdopodobieństwo, że taki graf ma pewną żądaną cechę.
Należy mieć świadomość, że konstrukcja przestrzeni probabilistycznej wymaga uwagi. Możemy utożsamić grafy losowe z ciągami zero-jedynkowymi i traktować je jak liczby rzeczywiste z przedziału \([0,1]\). Pytanie o to, czy graf losowy ma żądaną własność, sprowadzamy w ten sposób do pytania o miarę Lebesgue’a podzbiorów odcinka jednostkowego. Pozwolę sobie jednak pominąć mniej istotne szczegóły techniczne.
Wprowadźmy następującą własność:
Dla dowolnych skończonych i rozłącznych i skończonych zbiorów wierzchołków \(U, W \subset V\) istnieje wierzchołek \(v \in V\), który sąsiaduje ze wszystkimi wierzchołkami z \(U\) oraz z żadnym wierzchołkiem z \(V\).
Lemat 1. Prawdopodobieństwo, że graf losowy ma własność \((\triangle)\) jest równe \(1\).
Sprawdzimy, że dopełnienie rozważanego zdarzenia ma prawdopodobieństwo równe \(0\). Ponieważ różnych par \((U,W)\) utworzonych z rozłącznych i skończonych zbiorów \(U\) i \(W\) jest przeliczalnie wiele, wystarczy, że wykażemy tezę dla dowolnie wybranej pary. Przyjmijmy, że zbiory \(U\) i \(W\) mają łącznie \(n\) wierzchołków. To, czy wierzchołek \(v \in V\) ma cechę opisaną w \((\triangle)\), jest zdeterminowane przez wzajemną relację między \(v\) a wierzchołkami w \(U \cup W\). Ponieważ krawędzie losujemy niezależnie, to prawdopodobieństwo tego, że wierzchołek \(v\) nie ma żądanej własności, jest równe \(1 - 2^{-n}\). Oznaczając przez \(A_k\) zdarzenie: \[\text{żaden z~wierzchołków \( v_1, \dots, v_k \) nie spełnia \( (\triangle) \)},\] widzimy, ponownie wykorzystując niezależność, że jego prawdopodobieństwo jest równe \((1 - 2^{-n})^k\). To implikuje \(\lim_{k \to +\infty} P(A_k) = 0\) i kończy dowód lematu, gdyż własność \((\triangle)\) zachodzi wtedy i tylko wtedy, gdy zachodzi dopełnienie zdarzenia \(\lim_{k \to +\infty} A_k = \bigcup_{k = 1}^{+\infty} A_k\).
Jeżeli przeliczalnie wiele zdarzeń ma prawdopodobieństwo \(0\), to ich suma również.
Dla pełnej ścisłości powinniśmy się w tym miejscu powołać na ciągłość miary prawdopodobieństwa \(P\).
Sam lemat nie robi może wielkiego wrażenia, ale wynika z niego bezpośrednio, że istnieje tylko jeden nieskończony graf losowy!
Przypominamy, że rozważamy tylko przeliczalne grafy nieskończone.
Twierdzenie 2 (Erdős-Rényi, 1963 r.). Dwa nieskończone grafy losowe są izomorficzne z prawdopodobieństwem \(1\).
Proof. Niech \(G = (V,E)\) i \(G' = (V',E')\) będą nieskończonymi grafami losowymi. Wykorzystując technikę tam i z powrotem, zbudujemy izomorfizm \(f\) między nimi.
Przyjmijmy, że \(V = \lbrace{ v_1,v_2,\ldots \rbrace}\) i \(V' = \lbrace{ w_1,w_2,\ldots \rbrace}\), i połóżmy \(f(v_1) = w_1\). Rozważmy wierzchołek \(w_2\) i znajdźmy w grafie \(G\) wierzchołek \(v_i\) o tej własności, że \(v_1v_i \in E\) wtedy i tylko wtedy, gdy \(w_1w_2 \in E'\). Niech \(f(v_i) = w_2\). Przejdźmy do wierzchołka \(v_2\) (lub \(v_3\), w razie gdyby \(v_i = v_2\)), i znajdźmy w grafie \(G'\) wierzchołek \(w_j\), który jest w tej samej relacji do \(w_1\) i \(w_2\) co \(v_2\) do \(v_1\) i \(v_i\) – chcemy, aby grafy złożone z wierzchołków \(\lbrace{v_1,v_i,v_2\rbrace}\) i \(\lbrace{ w_1,w_2,w_j \rbrace}\) były izomorficzne. Definiujemy \(f(v_2) = w_j\).
Taki wierzchołek istnieje z prawdopodobieństwem \(1\) na mocy lematu.
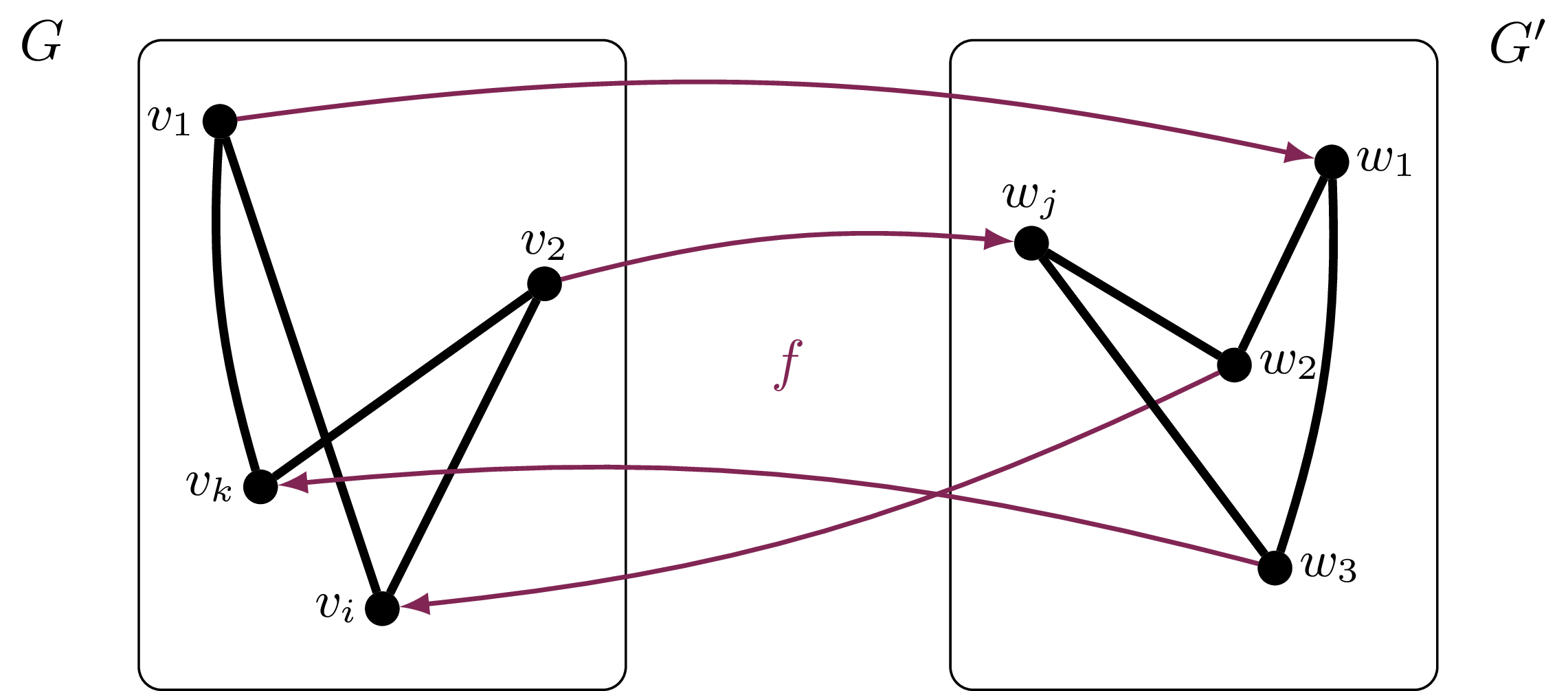
Powtarzamy opisaną procedurę w nieskończoność. W kroku o numerze nieparzystym (tam) znajdujemy pierwszy wierzchołek w zbiorze \(V\), powiedzmy \(v_n\), na którym funkcja \(f\) nie została jeszcze określona. Podzielmy zbiór wierzchołków, na których funkcja \(f\) jest już określona, na dwie części: niech \(U\) zawiera sąsiadów \(v_n\), a \(W\) resztę. Połóżmy \(U' = f(U)\) i \(W' = f(W)\). Zbiory \(U'\) i \(W'\) są skończone i rozłączne, bo takie też są zbiory \(U\) i \(W\). Z lematu wiemy, że istnieje w grafie \(G'\) wierzchołek, który sąsiaduje ze wszystkimi wierzchołkami z \(U'\) i żadnym wierzchołkiem z \(W'\). Wybierzmy taki wierzchołek o najmniejszym indeksie, powiedzmy \(w_m\), i zdefiniujmy \(f(v_n) = w_m\).
Podkreślamy, że \(U \cup W\) zawiera tylko te wierzchołki, na których \(f\) została już zdefiniowana.
Analogicznie postępujemy w kroku o numerze parzystym (z powrotem). Niech \(w_n\) będzie pierwszym wierzchołkiem w zbiorze \(V'\), który nie jest wartością funkcji \(f\). Aktualny zbiór wartości funkcji \(f\) dzielimy na sąsiadów \(U'\) wierzchołka \(w_n\) i resztę \(W'\). Następnie znajdujemy w grafie \(G\) odpowiednik \(v_m\) wierzchołka \(w_n\), który sąsiaduje ze wszystkimi wierzchołkami z \(f^{-1}(U')\) i nie sąsiaduje z żadnym wierzchołkiem z \(f^{-1}(W')\). Przyjmujemy \(f(v_m) = w_n\).
Bezpośrednio z konstrukcji funkcji \(f\) widać, że jest ona bijekcją między zbiorami wierzchołków \(G\) i \(G'\) i zadaje poszukiwany izomorfizm. ◻
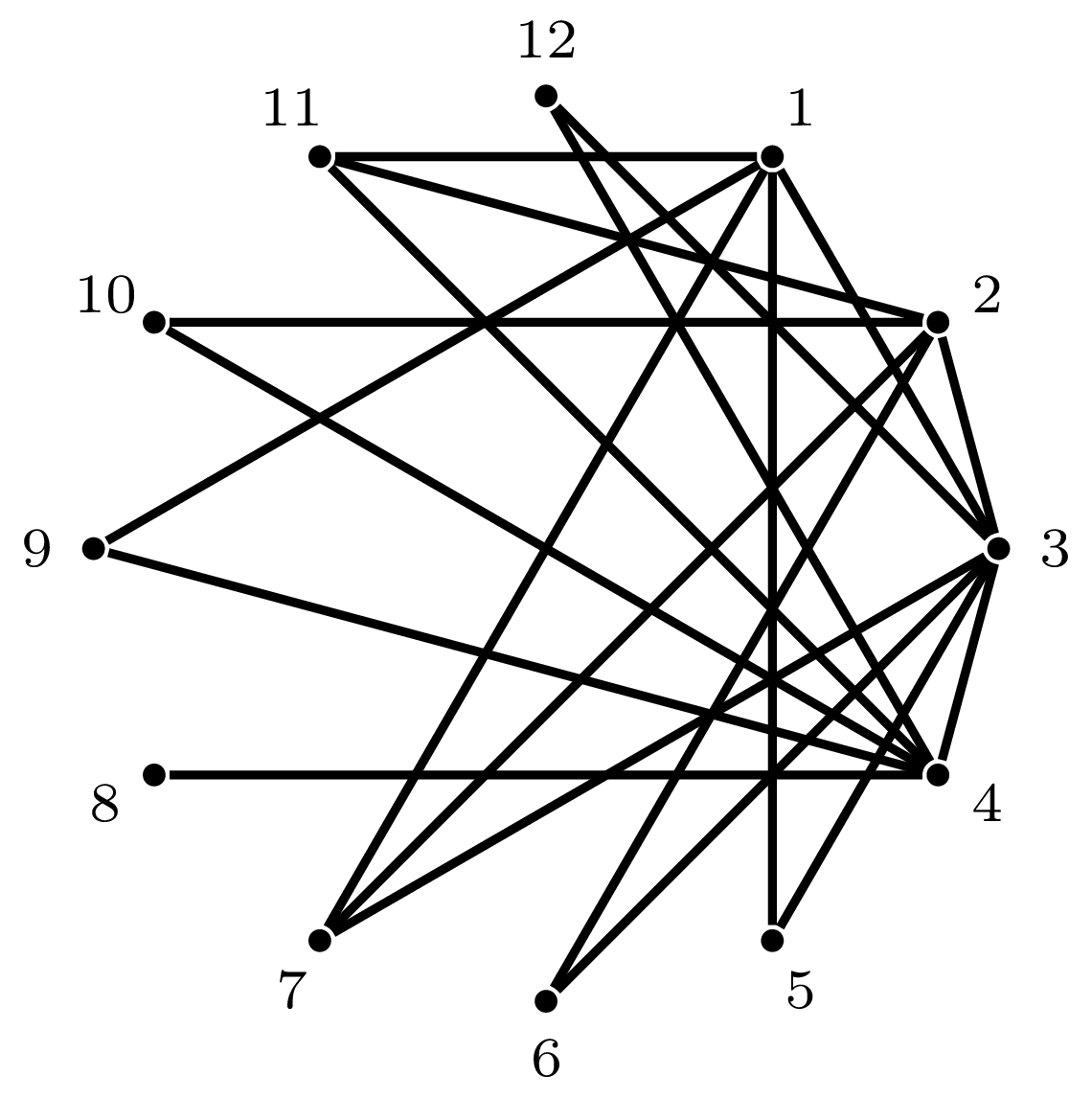
Erdős i Rényi pokazali, że w pewnym sensie istnieje tylko jeden nieskończony graf losowy – jest to graf określony przez warunek \((\triangle)\). Nie wskazali jednak żadnego konkretnego egzemplarza. Pierwszy przykład został skonstruowany przez Richarda Rado w 1964 roku. Graf Rado jest niezwykle urokliwy. Zbiorem wierzchołków jest \(V = % \mathbb N\), a \(m,n \in V\), \(m < n\) są połączone krawędzią wtedy i tylko wtedy, gdy w zapisie dwójkowym liczby \(n\) na \(m\)-tym miejscu od prawej strony występuje \(1\). Dla przykładu wierzchołki 4 i 10 są połączone krawędzią, ponieważ zapis dwójkowy liczby 10, czyli \((1010)_2,\) ma na 4. miejscu od prawej strony jedynkę. Uzasadnijmy, że tak skonstruowany graf ma własność \((\triangle)\). Niech \(U,W \subset V\) będą skończone i rozłączne. Dodając w razie potrzeby nowy wierzchołek do \(U\), możemy przyjąć, że \(\max U > \max W\). Wystarczy teraz zauważyć, że \(v = \sum_{u \in U} 2^{u-1}\) ma własność opisaną w \((\triangle)\).
Graf Rado przy obcięciu do pierwszych 12 wierzchołków