Każdy układ izolowany dąży do równowagi termodynamicznej. Po tym stwierdzeniu niemal zawsze następuje przykład gorącego kubka z herbatą. Nie bez powodu zresztą – nawet osoby, które nigdy w życiu nie słyszały o zasadach termodynamiki, wiedzą, że w chłodnym pokoju gorąca herbata zawsze stygnie, natomiast zimna herbata raczej nie zacznie się gotować. Ta asymetria wyznacza kierunek upływu czasu, zwany powszechnie strzałką czasu (o której można więcej przeczytać w \(\Delta^{1}_{19}\)). Skoro zatem bieg czasu w przeciwnym kierunku dałby nam niefizyczny proces, to stygnięcie herbaty jest procesem nieodwracalnym i jako taki wiąże się ze zwiększeniem entropii naszego systemu (więcej o entropii można przeczytać w \(\Delta^{4}_{19}\)). Gdy temperatura w kubku i pokoju wreszcie się wyrówna, system dochodzi do tzw. stanu równowagi termodynamicznej, czyli osiąga najbardziej prawdopodobny stan makroskopowy (stan o najwyższej entropii). Ta powszechna w układach fizycznych chęć dążenia do równowagi termodynamicznej ujęta jest przez drugą zasadę termodynamiki, która głosi, że entropia w układach izolowanych samorzutnie nie maleje.
Sam stan równowagi termodynamicznej ma dwie szczególne właściwości. Po pierwsze jest stanem stacjonarnym, a po drugie zachodzi w nim zasada równowagi szczegółowej. Wyjaśnimy teraz pokrótce te pojęcia. Gdy opisujemy obiekty złożone z ogromnej liczby cząstek, nie jesteśmy w stanie śledzić ruchu każdej z nich. Zamiast tego opisujemy układ za pomocą prawdopodobieństwa, na przykład tego, że w gazie jest cząstka o konkretnej prędkości. Stan stacjonarny jest to stan, w którym rozkład prawdopodobieństwa różnych konfiguracji układu nie zmienia się w czasie. W konsekwencji makroskopowe parametry układu, takie jak średnia temperatura, średnie ciśnienie czy średnia gęstość cząstek, pozostają stałe.
Ale stan równowagi termodynamicznej jest czymś więcej niż tylko stanem stacjonarnym. Cząsteczki gazu są w ciągłym ruchu, więc pomimo tego, że średnia gęstość jest stała, to gęstości cząstek fluktuują i układ przechodzi przez różne konfiguracje. W przypadku równowagi szczegółowej każdej zmianie w mikroskopowej konfiguracji odpowiada równie prawdopodobna zmiana w odwrotnym kierunku. Dlatego też ewolucja układu w stanie równowagi termodynamicznej jest taka sama zarówno “do przodu”, jak i “do tyłu”. Ponieważ dynamika nie wyróżnia kierunku w czasie, to układ w stanie równowagi termodynamicznej nie wyróżnia strzałki czasu. Natomiast układ, który jest tylko w stanie stacjonarnym, w ogólności może taką strzałkę wyróżniać. Dla układu w stanie stacjonarnym, który nie jest w stanie równowagi termodynamicznej, powstaje więc pytanie – jak bardzo dynamika tego układu jest nieodwracalna? Na to pytanie postaramy się tu znaleźć odpowiedź.
Mierzenie nieodwracalności procesów jest istotne nie tylko w fizyce, ale też w biologii. W publikacji [\(*\)], która zainspirowała nas do napisania tego artykułu, Autorzy analizowali odpowiedzi komórek siatkówki oka salamandry na różne bodźce wizualne. Przy odpowiednio silnym pobudzeniu komórki nerwowe wysyłają impuls prądowy, który nazywamy potencjałem czynnościowym, do następnych komórek. Powstanie takiego impulsu możemy obserwować w postaci zmiany potencjału elektrycznego wewnątrz neuronu i rejestrować za pomocą elektrod. Bodźce wizualne składały się z nagrań ze środowiska naturalnego (łamiące symetrię czasową) oraz poziomego paska poruszającego się losowo w górę i w dół (odwracalne czasowo). Okazało się, że nieodwracalność powstałych impulsów pojawiała się przy wszystkich rodzajach bodźców. Najbardziej nieoczywistym wynikiem było jednak to, że największa nieodwracalność w grupach komórek powstawała, gdy sam bodziec był najbardziej odwracalny. Formalizm wprowadzony przez autorów pozwala też określić źródło tej nieodwracalności. Wyniki pokazały, że jej głównym źródłem były interakcje pomiędzy neuronami, a nie cechy samego źródła.
W tym artykule, podążając za pracą [\(*\)], przybliżymy Czytelnikom, w możliwie łagodny sposób, metodę kwantyfikacji nieodwracalności w układach złożonych.
Wygodnym narzędziem do opisu procesów dynamicznych są łańcuchy Markowa. Czytelników, którzy chcieliby dowiedzieć się, czym te łańcuchy są, lub odświeżyć swoją wiedzę na ten temat, zapraszamy do przeczytania poświęconych im artykułów w \(\Delta^9_{13}\) i \(\Delta^{12}_{13}\). Niech \[T(x’|x) = P(X_n = x' | X_{n-1} = x)\] oznacza prawdopodobieństwo, że układ jest w stanie \(x’,\) pod warunkiem, że w poprzedniej chwili był w stanie \(x.\) Interpretujemy je jako prawdopodobieństwo przejścia ze stanu \(x\) do \(x’.\) Z twierdzenia Bayesa wynika, że \[T(x’|x) = \frac{P(X_n=x',X_{n-1}=x)}{P(X_{n-1}=x)},\] gdzie \(P(X_n = x’, X_{n-1} = x)\) oznacza prawdopodobieństwo, że w jednej chwili układ był w stanie \(x,\) a w kolejnej w \(x’,\) natomiast \(P(x_n = x)\) prawdopodobieństwo, że w pewnej chwili układ jest w stanie \(x.\) Prawdopodobieństwa te mogą zmieniać się w czasie (z powodu przejść pomiędzy stanami). Jeśli prawdopodobieństwa te się nie zmieniają, określają rozkład stacjonarny, a o samym procesie mówimy, że znajduje się w stanie stacjonarnym. Rozkład stacjonarny \(\pi(x)\) musi zatem spełniać następującą równość: \[\tag{1} \label{stationary_state} \begin{aligned}[t] \pi(x') &= P(X_n=x')= \sum_{x \in \Omega} P(X_n=x',X_{n-1}=x)= \\ &=\sum_{x \in \Omega} P(X_n=x'|X_{n-1}=x)P(X_{n-1}=x)=\\&= \sum_{x \in \Omega} T(x'|x) \pi(x). \end{aligned}\]
Wielkość \(P (X_{n-1} = x, X_n = x') = T(x'|x) \pi(x)\) będziemy nazywali całkowitym prawdopodobieństwem przejścia i oznaczali przez \(P(x\rightarrow x').\) Powiemy natomiast, że proces jest w stanie równowagi szczegółowej, gdy nie jesteśmy w stanie wyróżnić kierunku upływu czasu, to znaczy gdy \(P(x\rightarrow x')=P(x'\rightarrow x)\) dla dowolnych \(x,x'\in\Omega.\) Zauważmy, że taki stan musi być również stanem stacjonarnym, gdyż wówczas \[\tag{2}\label{cokolwiek} \sum_{x \in \Omega} T(x'|x) \pi(x)= \sum_{x \in \Omega} T(x|x') \pi(x')= \pi(x')\sum_{x \in \Omega} T(x|x')=\pi(x').\] Zależność odwrotna nie jest jednak prawdziwa, przykłady zobaczymy w dalszej części artykułu. Jak możemy zmierzyć poziom nieodwracalności procesu? Jednym z wyborów jest tak zwana entropia względna, określona wzorem
Entropia względna jest również znana jako dywergencja Kullbacka–Leiblera rozkładu \(P\) względem \(Q,\) \[D_{KL} (P || Q) = \sum_{x \in \Omega} P(x) \log \frac{P(x)}{Q(x)}.\]
\[\tag{3} \label{calkowita_nieodwracalnosc} \dot{I} = \sum_{x, x' \in \Omega} P(x\rightarrow x') \log \frac{P(x \rightarrow x')}{P(x' \rightarrow x)} \textrm{.}\] Można pokazać, że względna entropia \(\dot{I}\) jest zawsze nieujemna, a równowaga szczegółowa zachodzi wtedy i tylko wtedy, gdy \(\dot{I} = 0.\)
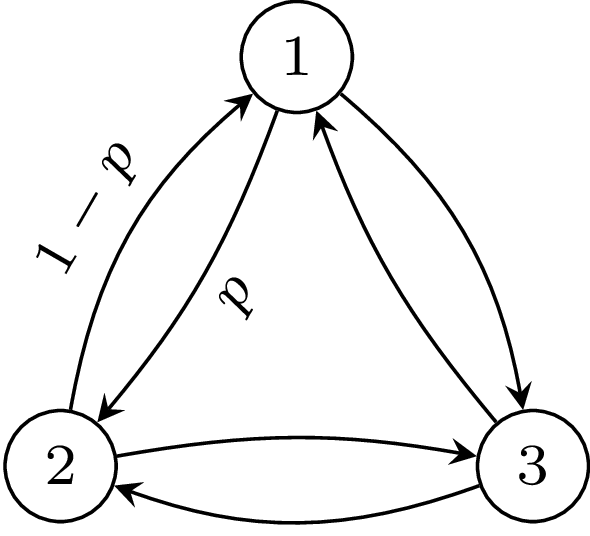
Rys. 1. Łańcuch Markowa o prawdopodobieństwach przejścia określonych przez macierz \[_{i,j\leq 3}= \begin{bmatrix} 0 & p & 1-p\\ 1-p & 0 & p\\ p & 1-p & 0 \end{bmatrix}\ \ \ \]
Zobaczmy, jak to działa w praktyce. Prosty przykład nieodwracalnego łańcucha jest przedstawiony na rysunku 1. Przestrzeń stanów składa się z trzech stanów \(\Omega = \{1,2,3\}.\) Prawdopodobieństwo przejścia w jednym kierunku wynosi \(p,\) natomiast w kierunku przeciwnym \(q\) (\(p+q=1\)). W naszej notacji \(T(x+1|x) = p,\) a \(T(x-1|x) = q\) dla \(x \in \Omega\) (działania wykonywane są modulo 3). Z definicji \(\eqref{stationary_state}\) rozkładu stacjonarnego dostajemy po prostych obliczeniach \(\pi(x) = 1/3\) dla każdego z trzech stanów. Nieodwracalność tego procesu wynosi natomiast: \[\dot{I} = \sum_{x, x' \in \{1,2,3 \}} P(x \rightarrow x') \log \frac{P(x\rightarrow x')}{P(x' \rightarrow x)} = 3 \cdot \frac{1}{3} p \log \frac{p}{q} + 3 \cdot \frac{1}{3} q \log \frac{q}{p} = (p-q) \log \frac{p}{q} \textrm{.}\] W sytuacji, gdy \(p=q,\) proces jest odwracalny i \(\dot{I} = 0.\) Niezależnie od wyboru \(p\) zawsze mamy \(\dot{I} \geq 0.\)
W pracy [\(*\)] autorzy pokazują, jak rozszerzyć przedstawiony wyżej formalizm, by dowiedzieć się czegoś o korelacjach i oddziaływaniach pomiędzy rożnymi częściami całego układu. By zilustrować to podejście, podzielmy układ na dwie części, które oznaczymy \(X\) i \(Y,\) i niech odpowiadające im zbiory możliwych stanów to \(\Omega_X, \Omega_Y.\) Całkowite prawdopodobieństwo przejścia układu pomiędzy stanami \((x,y)\) i \((x', y')\) będziemy oznaczać przez \[P\big((x,y) \rightarrow (x',y')\big) = P \big((X_{n+1},Y_{n+1}) = (x',y'), (X_n,Y_n) = (x,y)\big).\] W takiej sytuacji całkowita nieodwracalność układu przedstawia się tak jak poprzednio, zgodnie ze wzorem \(\eqref{calkowita_nieodwracalnosc}\), przy czym suma po stanach całego układu oznacza sumowanie zarówno po \(x,\) jak i \(y.\) Na potrzeby dalszych rozważań dołożymy pewne ograniczenie, mianowicie w danym kroku czasowym swój stan zmienia co najwyżej jeden z podukładów, tzn. \(X_{n+1} = X_n\) lub \(Y_{n+1} = Y_n.\) Przyjmiemy ponadto oznaczenie \(P(x\rightarrow x',y)=P\big((x,y) \rightarrow (x',y)\big).\)
Ponieważ nasz cały system składa się z kilku podukładów, jego całkowita nieodwracalność powinna być sumą nieodwracalności pochodzących z części składowych. Możemy zatem zdefiniować nieodwracalności dla indywidualnych podukładów, patrząc na ich dynamikę z pozostałymi podukładami pozostającymi w niezmienionym stanie. W naszym przypadku dwóch podukładów nieodwracalność w podukładzie \(X\) obliczymy w następujący sposób: \[\dot{I}_X = \sum_{y \in \Omega_Y} \sum_{x, x' \in \Omega_X} P(x \rightarrow x', y) \log \frac{P(x \rightarrow x', y)}{P(x' \rightarrow x, y)},\] i analogicznie określamy \(\dot{I}_Y.\) Zgodnie z wcześniejszym założeniem przejścia \((x,y)\rightarrow(x',y')\) dzielą się na takie, w których zmienia się tylko \(x,\) oraz takie, w których zmienia się tylko \(y,\) skąd łatwo wywnioskować równość \(\dot{I} = \dot{I}_X + \dot{I}_Y.\)
Może też zdarzyć się tak, że kilka układów fizycznych oddziałuje ze sobą, wpływając nawzajem na swoją dynamikę. W takim przypadku możemy patrzeć albo na wszystkie układy na raz, albo wybrać jeden z nich i badać tylko jego dynamikę, sumując po wszystkich pozostałych stopniach swobody. Zasadne jest zatem pytanie, ile dowiemy się o nieodwracalności systemu, stosując każde z tych podejść. Wielkość \(\dot{I}_X\) jest nieodwracalnością w pierwszym podukładzie i zależy od interakcji między podukładami przez to, że prawdopodobieństwo przejścia \(P(x \rightarrow x', y)\) zależy od stanu \(y\) drugiego układu i vice versa. Co się stanie, gdy spojrzymy na prawdopodobieństwo \(P(x \rightarrow x')\) przejścia \(x \rightarrow x'\) niezależnie od stanu drugiego podukładu? Wartość \(P(x \rightarrow x')\) otrzymamy, sumując po stanach drugiego podukładu: \[P(x \rightarrow x') = \sum_{y \in \Omega_Y} P(x\rightarrow x', y).\] Korzystając z tych prawdopodobieństw, możemy zdefiniować nieodwracalność podukładu, która, z samej konstrukcji, jest niezależna od stanu drugiego podukładu: \[\dot{I}_{\rm ind}^X = \sum_{x, x' \in \Omega_X} P(x \rightarrow x') \log \frac{P(x \rightarrow x')}{P(x' \rightarrow x)}.\] Analogicznie określamy \(\dot{I}_{\rm ind}^Y,\) definiujemy ponadto \(\dot{I}_{\rm ind} = \dot{I}_{\rm ind}^X + \dot{I}_{\rm ind}^Y.\)
Mając pełną wiedzę o stanie naszego układu (tzn. o stanach wszystkich jego podukładów), uzyskujemy również całą wiedzę o jego nieodwracalności. W konsekwencji \(\dot{I}_X\) jest całkowitą nieodwracalnością związaną z pierwszym podukładem. Ignorując pozostałe stopnie swobody, naturalnie tracimy część informacji. Dotyczy to również nieodwracalności podukładu. Tracona w ten sposób nieodwracalność związana jest z interakcją między podukładem, który nas interesuje, a resztą systemu. Prowadzi nas to do pojęcia nieodwracalności interakcji \(\dot{I}^{i}_{\rm int} \equiv \dot{I}^{i} - \dot{I}^{i}_{\rm ind}.\) Okazuje się, że tej nieodwracalności można nadać następującą interpretację: opisuje ona miarę informacji, jaką otrzymujemy o stanie całej reszty systemu, porównując dynamikę ustalonego podsystemu z dynamiką przy odwróconym kierunku czasu. Przy dwóch podukładach wyraża się to wzorem \[\dot{I}^X_{\rm int} = \sum_{y \in \Omega_Y} \sum_{x, x' \in \Omega_X} P(x\rightarrow x', y) \log \left[ \frac{P (y | x\rightarrow x')}{P (y | x'\rightarrow x)} \right]\textrm{,}\] gdzie \(P (y | x\rightarrow x') = P(x\rightarrow x', y) / P(x \rightarrow x').\) Nieodwracalność interakcji jest więc zerowa tylko wtedy, gdy puszczenie podukładu do przodu i do tyłu daje nam taką samą informację o reszcie systemu. W przeciwnym wypadku nieodwracalność interakcji podukładu jest ściśle dodatnia.
Oczywiście formalizm ten można rozszerzyć na systemy składające się z wielu różnych podukładów, gdzie możemy rozważać całą hierarchię nieodwracalności, z nieodwracalnością indywidualną na dole, a nieodwracalnością całkowitą na samej górze. Samą nieodwracalność interakcji możemy wówczas rozdzielić na interakcję drugiego rzędu, gdzie, tak jak wyżej, rozważamy jeden podukład, który zmienia stan, i jeden, którego stan jest ustalony, oraz trzeciego rzędu, gdzie dwa podukłady mają ustalone stany, i tak dalej.
By zobrazować ten podział, rozważmy tak zwany sensing system – układ złożony z dwóch podukładów: pierwszy wykonuje pewien losowy proces, a drugi stara się kopiować stan pierwszego. Jako pierwszy podukład \(X\) wybierzmy ponownie 3-stanowy proces Markowa z rysunku 1. Podukład \(Y\) kopiuje aktualny stan procesu \(X\) z prawdopodobieństwem \(p_y,\) zaś z prawdopodobieństwami \(\frac{1}{2}(1-p_y)\) wybiera każdy z pozostałych stanów. Za każdym krokiem czasowym podukład podlegający ewolucji jest wybierany losowo, każdy z prawdopodobieństwem \(\frac{1}{2}.\) Przykładową ewolucję obu układów prezentuje niniejsza tabelka, w której podkreśleniem zaznaczono układ podlegający zmianie, zaś ramką – sytuację, w której proces \(Y\) poprawnie skopiował proces \(X.\)
| X | \(\mid\) | 1 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 3 |
| Y | \(\mid\) | 1 | 1 | 1 | 3 |
2 | 2 | 1 | 2 |
2 | 2 | 2 |
Po zadaniu prawdopodobieństw przejść kolejnym krokiem jest znalezienie stanu stacjonarnego. Cały układ może teraz znajdować się w jednym z 9 stanów,
co oznacza, że stan stacjonarny jest rozwiązaniem układu \(9\) równań. Na szczęście dla naszego układu sytuacja się upraszcza. Ponieważ zasady ewolucji układu nie wyróżniają żadnego stanu, więc stan stacjonarny musi odzwierciedlać tę symetrię. Stąd wynika, że \(\pi(1,1) = \pi(2,2) = \pi(3,3) = \lambda,\) \(\pi(1,2) = \pi(2,3) = \pi(3,1) = \mu\) i \(\pi(1,3) = \pi(2,1) = \pi(3,2) = \nu.\) Prowadzi to do \(3\) równań na \(\lambda,\) \(\mu\) i \(\nu,\) których rozwiązaniem są: \[\begin{aligned} \lambda &= \frac{1}{N}(3 + 5p_y - 2p_x(1-p_x) ), \ \ \ \mu = \frac{1}{N}(5 - p_x - p_y + 2p_x^2 + 3 p_x p_y), \\ \nu &= \frac{1}{N}(6 - 3p_x - 4p_y + 2p_x^2 +3 p_x p_y), \end{aligned}\] Stała normująca \(N\) jest dobrana tak, by prawdopodobieństwa w stanie stacjonarnym sumowały się do \(1,\) czyli by \(\lambda + \mu + \nu = 1/3.\)
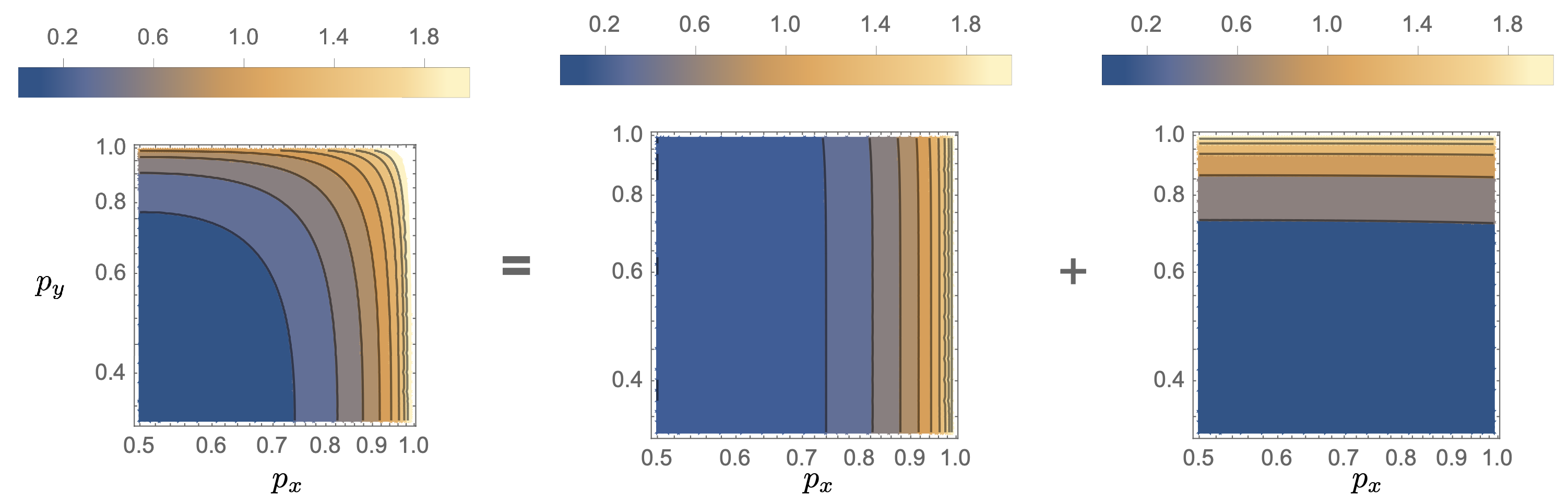
Znając stan stacjonarny, możemy obliczyć prawdopodobieństwa, że układ zmieni swój stan pomiędzy każdymi dwiema konfiguracjami. Na przykład prawdopodobieństwo, że układ był w stanie \((1, 1)\) i przeszedł do stanu \((1, 2),\) wynosi \(P(1, 1\rightarrow 2) = T(1, 2|1, 1) \pi(1,1).\) Natomiast prawdopodobieństwo, że podukład \(Y\) zmienił stan z \(1\) na \(2,\) wynosi \[P(1 \rightarrow 2) = T(1, 2|1, 1) \pi(1,1) + T(2, 2|2, 1) \pi(2,1) + T(3, 2|3, 1) \pi(3,1).\] Znając te prawdopodobieństwa, możemy obliczyć \(\dot{I}\) i \(\dot{I}_{\rm ind},\) na przykład \[\dot{I}_{\rm ind}^X = \frac{1}{2}\left(1-2 p_x\right) \log \frac{1-p}{p}, \ \ \ \dot{I}_{\rm ind}^Y = \frac{3}{4} (1-3 p_y) (\mu -\nu )\log {\left(\frac{1 -3 \nu - p_y +9 \nu p_y}{1 -3 \mu - p_y + 9 \mu p_y}\right)}.\] Wyrażenia na \(\dot{I}\) są bardziej skomplikowane i by zobrazować wyniki, posłużymy się wykresami. Na rysunku 2 przedstawiliśmy nieodwracalności w funkcji prawdopodobieństw \(p_x\) i \(p_y.\) Całkowita nieodwracalność zależy od obu zmiennych. Natomiast nieodwracalność niezależna \(\dot{I}_{\rm ind}\) i interakcji \(\dot{I}_{\rm int}\) zależą głównie od \(p_x\) i \(p_y,\) odpowiednio. Pokazuje to, że obie wielkości są czułe na różne aspekty dynamiki.
Gdyby ktoś z Czytelników postanowił obliczyć pozostałe nieodwracalności, okaże się, że nieodwracalności interakcji obu podukładów są dodatnie, pomimo że prawdopodobieństwa przejścia wewnątrz podukładu \(X\) zupełnie nie zależą od podukładu \(Y.\) Krótkie wyjaśnienie może być następujące. Obserwując tylko podukład \(X\) i jego asymetrię, możemy spodziewać się, że w podukładzie kopiującym asymetria ta będzie odwzorowana, choć z szumem. Tak samo, obserwując sam podukład \(Y,\) powinniśmy być w stanie wyciągnąć z niego pewną asymetrię, która będzie konsekwencją asymetrii układu \(X.\)
[*] Christopher W. Lynn, Caroline M. Holmes, William Bialek, and David J. Schwab. “Emergence of local irreversibility in complex interacting systems”. Phys. Rev. E, 106:034102, Sep 2022.
Podsumowując, wprowadzona przez autorów pracy [\(*\)] metoda pozwala na zmierzenie nieodwracalności. Wielkość ta mówi nam, jak daleko układ w stanie stacjonarnym jest od stanu równowagi termodynamicznej. Tym, co prowadzi do nieodwracalności, jest złamana zasada równowagi szczegółowej, co powoduje, że układ ewoluuje w konkretnym kierunku. Co ważne, metoda ta pozwala również określić źródło nieodwracalności – czy jest ona wynikiem dynamiki wewnątrz podukładów, czy jest efektem oddziaływań pomiędzy podukładami? Czekamy na kolejne zastosowania tej metody, by poznać jej pełen potencjał.