Delta 8/2024

Klub 44

Marcin E. Kuczma i Elżbieta Zawistowska

Redaguje Marcin E. KUCZMA

Rozwiązania zadań z numeru 4/2024

Przypominamy treść zadań:

879. Funkcje $f$ i $g,$ o wartościach rzeczywistych, są określone na przedziale $[a, b]$ ; funkcja $g$ jest rosnąca; $f (a) > 0 > f (b) .$ Wiadomo ponadto, że różnica $f - g$ jest funkcją ciągłą. Udowodnić, że w pewnym punkcie przedziału $(a, b)$ funkcja $f$ przyjmuje wartość 0.

Rozwiązanie

Niech $c$ będzie kresem górnym zbioru ${x \in [a, b] : f (x) \geq 0}$ (niepustego, bo $f (a) > 0$ ). Istnieje zatem ciąg $(x_{n})$ elementów tego zbioru (być może stały od pewnego miejsca), zbieżny od lewej strony do $c .$ Funkcja $g$ jest rosnąca, więc $g (x_{n}) \leq g (c)$ dla wszystkich $n .$ Funkcja $φ = f - g$ jest ciągła, więc $φ (x_{n}) \to φ (c)$ ; przy tym $φ (x_{n}) = f (x_{n}) - g (x_{n}) \geq 0 - g (c),$ skąd wniosek, że $φ (c) \geq - g (c),$ czyli $f (c) \geq 0 .$

Skoro (z założenia) $f (b) < 0,$ zatem $c < b .$ Z określenia liczby $c$ wynika, że dla $x \in (c, b]$ zachodzi nierówność $f (x) < 0$ ; a także nierówność $g (x) > g (c),$ bo $g$ jest funkcją rosnącą. Wobec tego $φ (x) = f (x) - g (x) < 0 - g (c)$ dla $x \in (c, b] .$ W granicy, gdy $x$ dąży do $c$ (od prawej strony), dostajemy $φ (c) \leq - g (c) .$

Uzyskane nierówności pokazują, że $φ (c) = - g (c)$ ; a to znaczy, że $f (c) = 0 .$

880. Rozstrzygnąć, czy zbiór wszystkich dodatnich liczb wymiernych $Q_{+}$ daje się przedstawić w postaci sumy dwóch zbiorów rozłącznych $A, B$ tak, by miały miejsce następujące implikacje (dla $x, y \in Q_{+}$ ): $∙$ jeśli $x y = 1,$ to $x \in A, y \in A$ lub $x \in B, y \in B$ ; $∙$ jeśli $| x - y | = 1,$ to $x \in A, y \in B$ lub $x \in B, y \in A .$

Rozwiązanie

Istnieje takie rozbicie. Opis metody: określamy funkcję $f : Q_{+} \to Q_{+}$ wzorami $f (x) = {\begin{cases} 1 / x =: f_{0} (x) & dla x \leq 1, \\ x - 1 =: f_{1} (x) & dla x > 1. \end{cases}$ Startujemy od dowolnej liczby $x \in Q_{+}$ i iterujemy przekształcenie $f$ (więc w każdym kroku stosujemy $f_{0}$ lub $f_{1},$ w zależności od tego, czy jesteśmy w przedziale $(0, 1],$ czy $(1, \infty)$ ). Zauważmy, że jeśli liczba wymierna (dodatnia) jest zapisana w postaci ułamka nieskracalnego, wówczas przy zastosowaniu funkcji $f_{1}$ suma licznika i mianownika zmniejsza się; zaś przy zastosowaniu $f_{0}$ ta suma nie ulega zmianie. Jednak po zastosowaniu $f_{0}$ jesteśmy w przedziale $(1, \infty)$ i w następnym kroku działamy znów funkcją $f_{1},$ zmniejszając sumę licznika i mianownika. Wniosek: po skończenie wielu krokach trafimy w liczbę 1. Kończymy wtedy procedurę iteracyjną.

Jeśli, startując od liczby $x,$ stosowaliśmy kolejno funkcje $f_{i_{1}}, f_{i_{2}}, \dots, f_{i_{k}},$ wówczas $(i_{1}, i_{2}, \dots, i_{k})$ jest ciągiem zerojedynkowym (skończonej długości), który możemy uważać za kod liczby $x .$

Przykład: dla $x = \frac{27}{98}$ dostajemy trajektorię $\frac{27}{98} \Rightarrow \frac{98}{27} \to \frac{71}{27} \to \frac{44}{27} \to \frac{17}{27} \Rightarrow \frac{27}{17} \to \frac{10}{17} \Rightarrow \frac{17}{10} \to \frac{7}{10} \Rightarrow \frac{10}{7} \to \frac{3}{7} \Rightarrow \frac{7}{3} \to \frac{4}{3} \to \frac{1}{3} \Rightarrow \frac{3}{1} \to \frac{2}{1} \to \frac{1}{1}$ (strzałka $\Rightarrow$ oznacza zastosowanie operacji $f_{0}$ ; strzałka $\to$ oznacza $f_{1}$ ). Kod liczby $\frac{27}{98}$ to $(0111010101011011) .$ [Można tu dostrzec rozbudowaną postać algorytmu Euklidesa].

Dla dowolnej liczby $x \in Q_{+}$ określamy $S (x)$ jako sumę symboli w jej kodzie: $S (x) = i_{1} + \dots + i_{k}$ (czyli liczbę jedynek; np. $S (\frac{27}{98}) = 10$ ; $S (1) = 0$ (kod pusty)). I teraz: jeśli $S (x)$ ma wartość parzystą, wrzucamy liczbę $x$ do zbioru $A$ ; jeśli nieparzystą – to do zbioru $B .$ Wymagane warunki są spełnione: gdy $x y = 1$ oraz (b.s.o.) $x < 1,$ to $y = f (x) = f_{0} (x)$ ; kody liczb $x,$ $y$ mają tyle samo jedynek, więc te liczby są obie w $A$ lub obie w $B .$ Gdy zaś $x - y = 1,$ to $y = f (x) = f_{1} (x),$ kody liczb $x,$ $y$ różnią się o jedną jedynkę, więc te liczby leżą jedna w $A,$ druga w $B .$

[Czytelnikowi Wnikliwemu proponujemy zastanowienie się, czy przedstawiona konstrukcja rozbicia $Q_{+} = A \cup B$ (o żądanej własności) jest jedyną możliwą (z dokładnością do zamiany symboli $A \leftrightarrow B$ )].

Redaguje Elżbieta ZAWISTOWSKA

Rozwiązania zadań z numeru 4/2024

Przypominamy treść zadań:

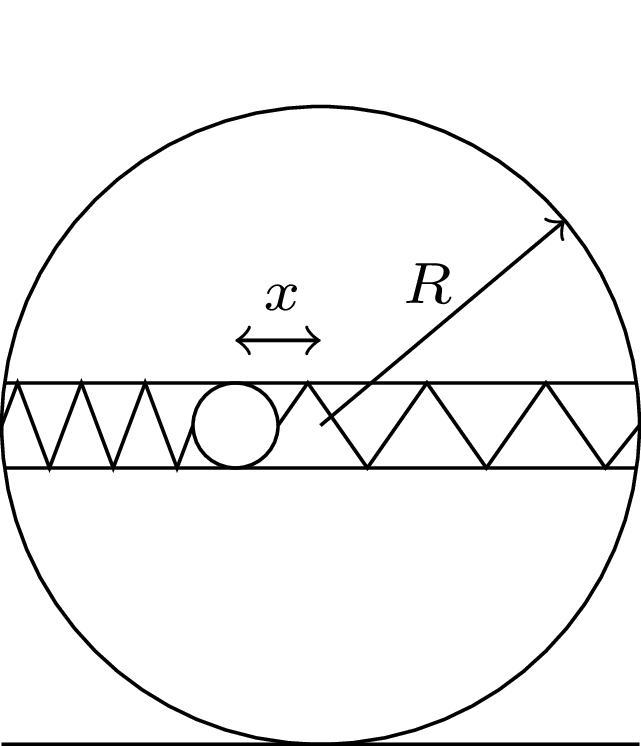
776. Na poziomej powierzchni stoi jednorodna, cienka obręcz o masie $M$ i promieniu $R .$ Poziomą średnicę obręczy stanowi lekka, gładka rurka, wewnątrz której umieszczono kulkę o masie $m$ przylegającą do rurki i połączoną z obręczą dwiema sprężynami o współczynnikach sprężystości $k$ (rys. 1). Przytrzymując obręcz, kulkę odchylono w lewo o $x,$ po czym układ pozostawiono samemu sobie. Znaleźć przyspieszenie środka obręczy w chwili początkowej, zakładając brak poślizgu obręczy.

Rozwiązanie

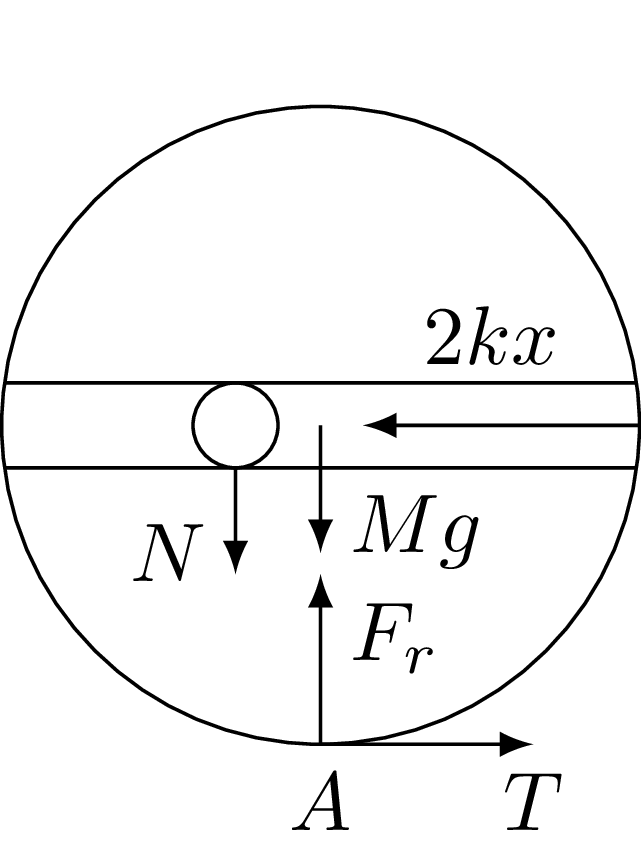
Na rysunku 3 zaznaczono siły działające na obręcz. Ponieważ nie występuje poślizg, możemy napisać równanie ruchu obrotowego obręczy wokół chwilowej osi obrotu przechodzącej przez punkt $A$ : $\begin{matrix} (1) & 2 M R^{2} ε = 2 k x R + N x, \end{matrix}$ gdzie $N$ jest siłą nacisku kulki na rurkę, $2 k x$ wypadkową siłą sprężystości.

Przyspieszenie kątowe $ε$ wiąże się z szukanym przyspieszeniem $a$ środka obręczy wzorem $\begin{matrix} (2) & ε = a / R . \end{matrix}$ Siłę nacisku $N$ znajdziemy z równania ruchu kulki w pionie: $\begin{matrix} (3) & m ε x = m g - N . \end{matrix}$ Z równań $(1)$ – $(3)$ otrzymujemy: $a = \frac{(m g + 2 k R) x R}{2 M R^{2} + m x^{2}} .$

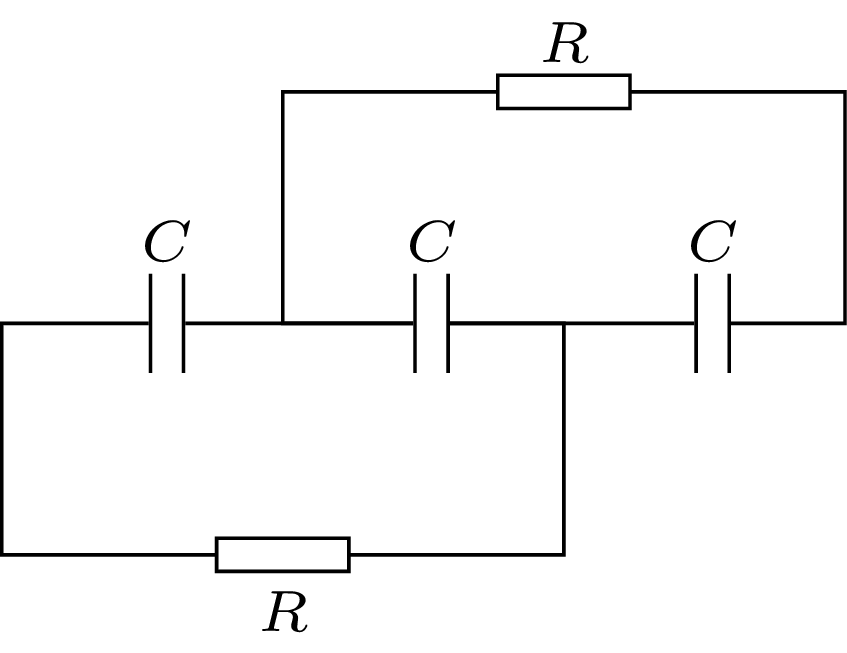
777. Trzy jednakowe kondensatory o pojemnościach $C$ połączono szeregowo, podłączono do źródła o sile elektromotorycznej $E$ i po naładowaniu odłączono od baterii. Następnie do układu podłączono jednocześnie dwa oporniki o oporach $R$ (rys. 2). Jaka ilość ciepła wydzieli się na każdym oporniku? Jakie natężenia mają prądy płynące przez oporniki w chwili, gdy napięcie na środkowym kondensatorze jest 10 razy mniejsze od siły elektromotorycznej baterii?

Rozwiązanie

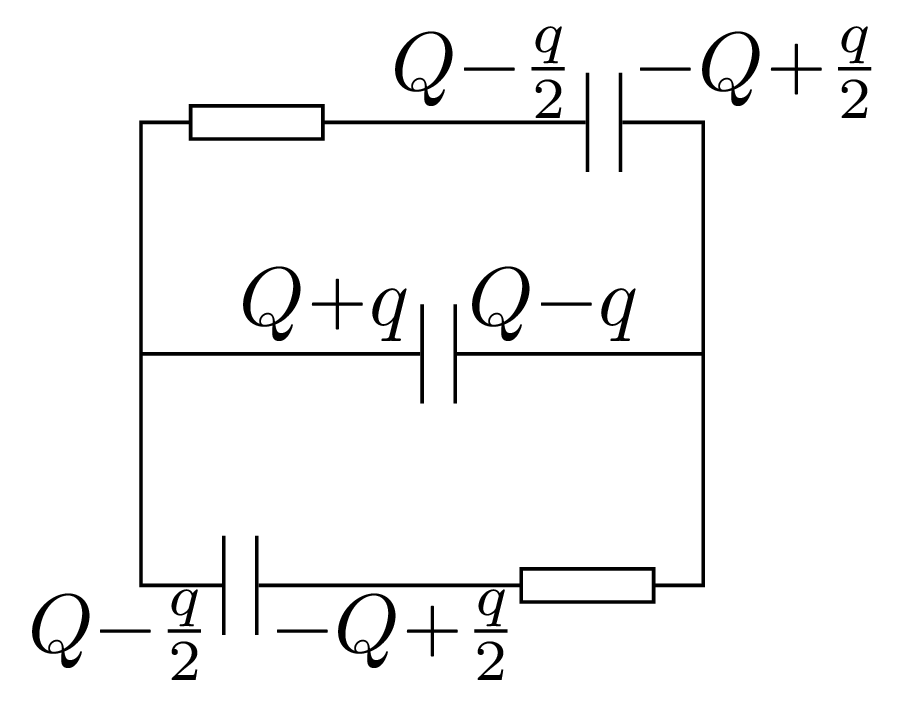
Ładunki na każdym z kondensatorów po odłączeniu baterii wynoszą $Q = C E / 3 .$ Po dołączeniu oporników, gdy prądy już nie płyną, kondensatory są połączone równolegle. Z dodatnio naładowanej okładki odpłynął ładunek $q$ i wpłynął na ujemnie naładowane okładki kondensatorów zewnętrznych (rys. 4). Ponieważ napięcia na kondensatorach są jednakowe, $Q - q = - Q + q / 2,$ stąd $q = 4 C E / 9 .$ Ładunki na prawych okładkach są równe $Q - q = - C E / 9 .$ Początkowa energia układu wynosi $W_{1} = 3 Q^{2} / 2 C = C E^{2} / 6,$ końcowa $W_{2} = C E^{2} / 54 .$ Ciepło wydzielone na każdym oporniku jest równe $W = (W_{1} - W_{2}) / 2 = 2 C E^{2} / 27.$ Ponieważ podczas przeładowywania zmieniają się znaki ładunków na środkowym kondensatorze, napięcie $E / 10$ pojawia się na nim dwukrotnie – podczas rozładowywania od $E / 3$ do zera i podczas ładowania od 0 do $E / 9 .$

Rozważmy przypadek pierwszy. Ładunek $q_{1}$ odpływający z okładki środkowego kondensatora znajdujemy z równania $Q - q_{1} = C E / 10,$ stąd $q_{1} = C E / 30 .$ Ładunek końcowy w rozważanym procesie na okładce kondensatora bocznego wynosi $- C E / 3 + q_{1} / 2 = - 13 C E / 60 .$ Z drugiego prawa Kirchhoffa dla dolnego oczka otrzymujemy: $E / 10 - R I_{1} + 13 E / 60 = 0,$ stąd szukane natężenie prądu $I_{1} = 19 E / 60 R .$

W drugim przypadku analogiczne równania mają postać: $Q - q_{2} = - C E / 10, - C E / 3 + q_{2} / 2 = - 7 C E / 60, - E / 10 - R I_{2} + 7 E / 60 = 0,$ a szukane natężenie $I_{2} = E / 60 R .$

Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
873 ( $W T = 1, 59$ ) i 874 ( $W T = 1, 69$ )
z numeru 1/2024

Paweł Kubit Kraków 45,24

Łukasz Merta Kraków 42,56

Szymon Kitowski 41,11

Adam Woryna Ruda Śl. 40,91

Piotr Kumor Olsztyn 40,44

Witold Bednarek Łódź 35,81

Krzysztof Zygan Lubin 34,43

Pan Paweł Kubit, od dawna nieprzerwanie obecny w Lidze, zakończył ósmą rundę!

Rys. 1

Rys. 2

Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
770 ( $W T = 3, 5$ ), 771 ( $W T = 2, 45$ ) z numeru 1/2024

Tomasz Rudny Poznań 1–44+1,96

Jacek Konieczny Poznań 40,41

Ryszard Baniewicz Włocławek 1–40,24

Konrad Kapcia Poznań 2–38,10

Paweł Perkowski Ożarów Maz. 5–33,59

Andrzej

Nowogrodzki Chocianów 3–23,69

Jan Zambrzycki Białystok 4–19,67

Tomasz Wietecha Tarnów 17–16,18

Paweł Kubit	Kraków	45,24
Łukasz Merta	Kraków	42,56
Szymon Kitowski		41,11
Adam Woryna	Ruda Śl.	40,91
Piotr Kumor	Olsztyn	40,44
Witold Bednarek	Łódź	35,81
Krzysztof Zygan	Lubin	34,43

Tomasz Rudny	Poznań	1–44+1,96
Jacek Konieczny	Poznań	40,41
Ryszard Baniewicz	Włocławek	1–40,24
Konrad Kapcia	Poznań	2–38,10
Paweł Perkowski	Ożarów Maz.	5–33,59
Andrzej
Nowogrodzki	Chocianów	3–23,69
Jan Zambrzycki	Białystok	4–19,67
Tomasz Wietecha	Tarnów	17–16,18