Afiliacja: University of Pittsburgh
A.S. is funded by NSF Career DMS-2044898
Czy przy mieszaniu łyżeczką gorącej kawy w filiżance zdarzyło Ci się kiedyś zastanowić, Czytelniku, nad skutecznością tego zabiegu? Mianowicie: czy jest możliwe, aby mimo starannego wymieszania jakaś pojedyncza cząstka kawy mogła znaleźć się dokładnie w tym samym miejscu, w którym była na początku? Jeśli wierzyć legendzie, holenderski matematyk Luitzen Egbertus Jan Brouwer (1881–1966) rzeczywiście się nad tym problemem zastanawiał, i zainspirowany przeprowadzonym eksperymentem dowiódł twierdzenia znanego dzisiaj jako twierdzenie Brouwera o punkcie stałym – pięknego wyniku łączącego w sobie topologię z analizą.
Dla uproszczenia przyjmiemy, że filiżanka jest dwuwymiarowa, jak na rysunku wyżej, choć analogiczne twierdzenie jest prawdziwe również w trzech wymiarach.
Przybliżmy sformułowanie interesującego nas twierdzenia. Weźmy dowolne ciągłe przekształcenie \(F\) z koła jednostkowego \({\mathbb{D}}\) w to samo koło. Przykładem jest tu przyporządkowanie każdej cząstce kawy \(\vec{p} \in {\mathbb{D}}\) jej położenia \(F(\vec{p})\) po wymieszaniu – koło \({\mathbb{D}}\) pełni tu rolę kształtu filiżanki. Twierdzenie orzeka, że istnieje wówczas co najmniej jeden punkt \(\vec{q},\) który nie ulega przemieszczeniu: \(F(\vec{q})= \vec{q}\) – co oznacza, że któraś cząstka kawy pozostała w miejscu.
Topologia: indeks krzywej
W Delcie pisaliśmy już o zastosowaniu pojęcia indeksu krzywej przy dowodzie podstawowego twierdzenia algebry (Maciej Skwarczyński, \(\Delta^{3}_{74}\)) i twierdzenia Borsuka–Ulama (Krzysztof Nowiński, \(\Delta^{11}_{75}\)).
Aby udowodnić twierdzenie Brouwera, zaczniemy od wprowadzenia na scenę naszego głównego narzędzia: indeksu. W tym celu weźmy ciągłe przekształcenie z okręgu w okrąg. Okrąg ten może reprezentować brzeg naszej (dla uproszczenia: dwuwymiarowej) filiżanki. Aby rozróżnić dziedzinę funkcji (okrąg przed mieszaniem) od jej przeciwdziedziny (okrąg po mieszaniu), oznaczymy je odpowiednio przez \(\mathbb{S}_1\) i \(\mathbb{S}_2.\)
Ciągłe przekształcenie \(f\) z \(\mathbb{S}_1\) (po lewej) w \(\mathbb{S}_2\) (po prawej) można przedstawić jako krzywą w \(\mathbb{S}_2.\) Aby lepiej zobaczyć jej zachowanie, wizualnie ,,pogrubiamy” \(\mathbb{S}_2.\) Zwróćmy uwagę na orientację: gdy poruszamy punktem \(\vec{v}\in \mathbb{S}_1\) zgodnie z ruchem wskazówek zegara, punkt \(f(\vec{v})\) porusza się w kierunku wskazanym przez strzałki.
Tak naprawdę lewy rysunek przedstawiający \(\mathbb{S}_1\) nie mówi nic o zachowaniu \(f,\) więc od teraz będziemy go pomijać.
Przekształcenie \(f\) to nic innego jak funkcja \(f \colon \mathbb{S}_1 \to \mathbb{S}_2.\) Ciągłość oznacza natomiast, że jeśli dwa punkty \(\vec{v}, \vec{u}\) w dziedzinie leżą blisko siebie, to \(f(\vec{v})\) nie może być zbyt daleko od \(f(\vec{u}).\) Takie ciągłe przekształcenie \(f\) będziemy też nazywać krzywą, bo możemy bez odrywania ołówka narysować wszystkie wartości \(f(\vec{v}),\) gdy \(\vec{v}\) przebiega \(\mathbb{S}_1.\) Ponieważ \(\mathbb{S}_1\) jest okręgiem, nie ma początku ani końca, podobnie jest więc z krzywą \(f\) zawartą w okręgu \(\mathbb{S}_2.\) Może przypominać ona gumkę recepturkę nawiniętą na \(\mathbb{S}_2.\)
Gdy założymy, że \(\vec{v}\) porusza się zgodnie z ruchem wskazówek zegara (w ten sposób ustalając orientację \(\mathbb{S}_2\)), to nasza gumka również jest zorientowana. Będzie dla nas ważne, by odróżniać poszczególne ,,pasma” gumki, więc w celu zwiększenia czytelności rysunki na marginesach przedstawiają ją na ,,pogrubionej” wersji okręgu \(\mathbb{S}_2.\)
Indeks krzywej równy \(1\)
Indeks krzywej równy \(2\)
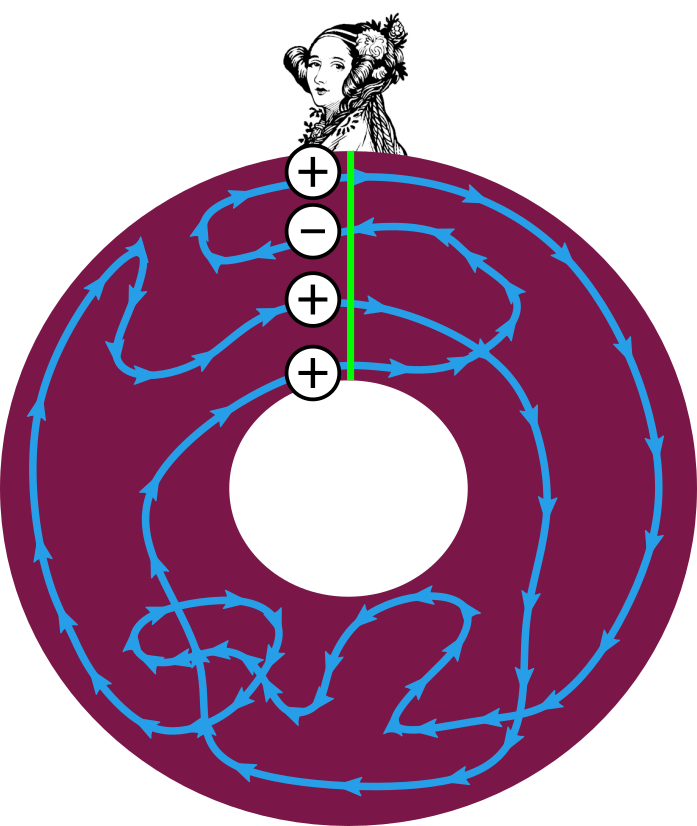
Czas na definicję. Przyjmijmy, że stoisz na górze okręgu \(\mathbb{S}_2\) i odnotowujesz, ile razy gumka przechodzi pod Twoimi nogami. Każde przejście zgodnie z ruchem wskazówek zegara liczy się jako \(+1,\) a każde przeciwne jako \(-1.\) Wynik takiego sumowania nazywamy indeksem krzywej \(f\) i oznaczamy przez \(\operatorname{ind}f.\) W zrozumieniu mogą pomóc przykłady na marginesie, a jeszcze bardziej – samodzielne narysowanie kolejnych.
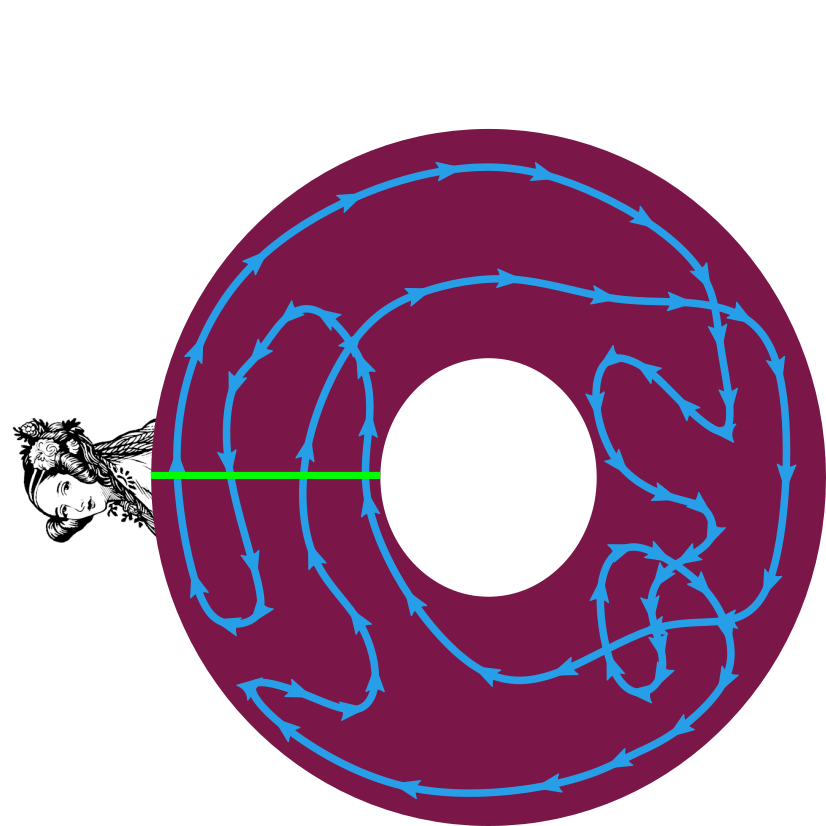
Ćwiczenie 1. Narysuj przykładowe krzywe o indeksie równym \(0,+1,-1,+2,-2,\ldots\) Znajdź kilka różnie wyglądających krzywych o indeksie \(2.\) Wyraź własnymi słowami: co mają wspólnego wszystkie krzywe o indeksie \(2.\)
Przy powyższym ćwiczeniu można się natknąć na dwie skrajne sytuacje. Po pierwsze, jeśli gumka nigdy Cię nie mija, współczynnik nawinięcia to po prostu zero. Skądinąd każde ,,dotknięcie”, gdy gumka do Ciebie dociera i od razu zawraca, liczy się jako \(0.\) Po drugie, dlaczego gumka nie miałaby nas mijać nieskończenie wiele razy? W takim przypadku jednak po prawie każdym przejściu gumka od razu zawraca i mija nas w przeciwną stronę; w rezultacie nieskończenie wiele \(+1\) i \(-1\) się wzajemnie znosi, pozostawiając skończoną sumę.
Przyjrzyjmy się jeszcze dwóm prostym, ale niezwykle ważnym przykładom:
Indeks krzywej równy \(0\)
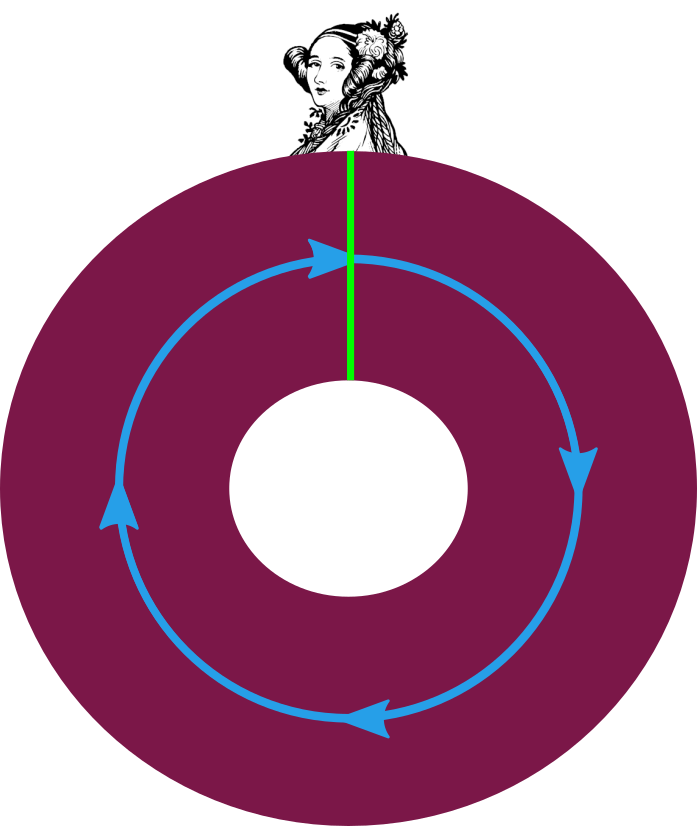
Przykład 1. Przyjmijmy, że przekształcenie \(f\) jest identycznością: \(f(\vec{v}) = \vec{v}.\) Wtedy gumka okrąża \(\mathbb{S}_2,\) zgodnie z ruchem wskazówek zegara, dokładnie raz. Indeks wynosi więc \(\operatorname{ind}f = 1.\)
Przykład 2. Ustalmy dowolny punkt \(\vec{u}\in \mathbb{S}_2\) i za \(h\) przyjmijmy przekształcenie stałe: \(h(\vec{v}) = \vec{u}.\) Gumka w ogóle nie okrąża wtedy \(\mathbb{S}_2,\) jest zdegenerowana do jednego punktu i dlatego \(\operatorname{ind}h = 0.\)
Przykład 1: Przekształcenie \(f(\vec{v}) = \vec{v}\) ma indeks równy \(1\)
Chociaż nie będzie to istotne dla dowodu, warto też wiedzieć rzecz następującą:
Przykład 2: Każde przekształcenie stałe ma indeks równy \(0\)
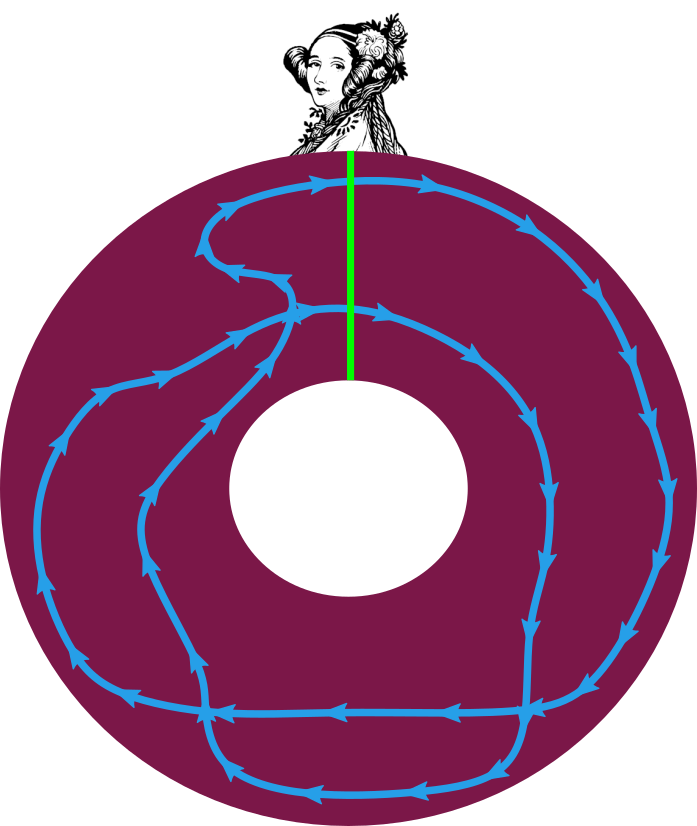
Ćwiczenie 2. Uzasadnij, że położenie obserwatora nie ma znaczenia: jeśli zamiast na górze okręgu będziemy stać w innym miejscu, wyznaczony przez nas indeks krzywej będzie taki sam.

Ćwiczenie 2: Niezależnie gdzie jest Ada, indeks jest taki sam
Wreszcie najważniejsza własność: ciągłe zmiany rozważanej krzywej nie zmieniają jej indeksu. Topologia ma osobną nazwę dla takiej ciągłej zmiany – to homotopia. Ponadto jeśli gumkę określoną przez \(f\) da się zdeformować do tej zadanej przez \(g,\) bez rozrywania i bez opuszczania \(\mathbb{S}_2,\) to przekształcenia \(f\) i \(g\) nazywamy homotopijnymi.
Ćwiczenie 3. Przekonaj się, że jeśli krzywą \(f\) przekształcimy w sposób ciągły w krzywą \(g\) – w trakcie tego procesu nie wychodząc poza \(\mathbb{S}_2\) – to indeks obu tych krzywych jest taki sam.
Ćwiczenie 3: Gdy jedną krzywą da się przekształcić w drugą bez rozrywania i opuszczania \(\mathbb{S}_2,\) indeks pozostaje ten sam. Ciekawostka: przeciwne wynikanie również jest prawdziwe!
Własność z ćwiczenia 3 może zostać wyrażona także w bardziej analityczny sposób:
Wniosek 4. Załóżmy, że przekształcenia \(f \colon \mathbb{S}_1 \to \mathbb{S}_2\) i \(g \colon \mathbb{S}_1 \to \mathbb{S}_2\) są ciągłe, a ponadto istnieje przekształcenie ciągłe zwane homotopią, \[H(t,\vec{v}) \in \mathbb{S}_2 \ \ \ \text{dla $0 \le t \le 1$ oraz $\vec{v}\in \mathbb{S}_2,$}\] spełniające następujące warunki:
\(H(0,\vec{v}) = f(\vec{v})\) dla wszystkich \(\vec{v}\in \mathbb{S}_1\);
\(H(1,\vec{v}) = g(\vec{v})\) dla wszystkich \(\vec{v}\in \mathbb{S}_1.\)
Wówczas indeks \(f\) jest równy indeksowi \(g.\)
Związek z ćwiczeniem 3 jest następujący. Dla każdej ,,chwili” \(t \in [0,1]\) funkcję \(\vec{v}\mapsto H(t,\vec{v})\) możemy traktować jako krzywą. Zmiana wartości \(t\) daje ciągłą zmianę tej krzywej, więc przekształcenie \(H\) opisuje ciągłą deformację krzywej \(f\) (w chwili \(t = 0\)) w krzywą \(g\) (w chwili \(t = 1\)).
Analiza: twierdzenie Brouwera o punkcie stałym
Zacznijmy od oznaczeń. Długość wektora \(\vec{p}= (x,y) \in \mathbb{R}^2\) oznaczamy przez \(|\vec{p}| := \sqrt{x^2+y^2},\) a domknięte koło jednostkowe przez: \[{\mathbb{D}}:= \{\text{wszystkie wektory } \vec{p}= (x,y) \in \mathbb{R}^2, \, \text{dla których } |\vec{p}| \leq 1 \}.\] Brzegiem koła \({\mathbb{D}}\) jest okrąg jednostkowy: \[\mathbb{S}:= \{\text{wszystkie wektory } \vec{p}= (x,y) \in \mathbb{R}^2, \, \text{dla których } |\vec{p}| = 1 \}.\] Użyjemy również oznaczenia \(\vec{0} = (0,0)\) na początek układu współrzędnych. Teraz już jesteśmy gotowi, by precyzyjnie sformułować twierdzenie Brouwera o punkcie stałym.
Twierdzenie 5. Dla dowolnego ciągłego przekształcenia \(F \colon {\mathbb{D}}\to {\mathbb{D}}\) istnieje co najmniej jeden punkt \(\vec{p}\in {\mathbb{D}}\) spełniający \(F(\vec{p}) = \vec{p}.\) Taki punkt \(\vec{p}\) nazywamy punktem stałym przekształcenia \(F.\)
Wróćmy na chwilę do filiżanki kawy z samego początku. Dla ułatwienia przyjmijmy, że filiżanka jest dwuwymiarowa, w kształcie koła \({\mathbb{D}}\) – tak jak widziana z góry na pierwszym rysunku. Przekształcenie \(F \colon {\mathbb{D}}\to {\mathbb{D}}\) możemy wtedy określić, rozważając kroplę kawy początkowo znajdującą się w punkcie \(\vec{p}\in {\mathbb{D}},\) i za \(F(\vec{p})\) przyjmując jej położenie po zamieszaniu. Oczywiście położenie to nadal jest w obrębie filiżanki \({\mathbb{D}}\) (nic się nie wylało!). W takiej sytuacji twierdzenie Brouwera stwierdza, że któraś z kropel kończy dokładnie tam, gdzie zaczęła.
Dowód Twierdzenia. Przeprowadzimy dowód przez sprzeczność, czyli założymy, że dane jest nam ciągłe przekształcenie \(F \colon {\mathbb{D}}\to {\mathbb{D}}\) pozbawione punktu stałego, i stąd wyprowadzimy sprzeczność. Na tej drodze pomoże nam wynikająca z braku punktu stałego obserwacja, że wielkość \(|\vec{p}-F(\vec{p})|\) jest dodatnia dla każdego \(\vec{p}\in {\mathbb{D}},\) a więc można przez nią dzielić bez obawy, że podzielimy przez zero. Posłuży nam to do zdeformowania gumki z przykładu 1 do tej z przykładu 2 i uzyskania w ten sposób sprzeczności z wnioskiem 4.
Konkretniej, do sprzeczności doprowadzi nas badanie indeksu krzywej \(g \colon \mathbb{S}_1 \to \mathbb{S}_2\) zadanej wzorem \(g(\vec{v}) := \frac{\vec{v}-F(\vec{v})}{|\vec{v}-F(\vec{v})|}.\) Skoro każdy punkt \(\vec{v}\) na okręgu jest również punktem koła, to ma sens rozważanie \(F(\vec{v}),\) a punkt powstały w wyniku dzielenia leży na okręgu \(\mathbb{S}_2.\) Ponadto nie dzielimy przez zero, więc funkcja \(g\) rzeczywiście jest dobrze określona i ciągła. Rozważymy trzy przekształcenia: \[\underbracket[0pt]{f(\vec{v}) = \vec{v},}_{\substack{{}\\[2mm] \text{jak w~przykładzie 1,} \\ \operatorname{ind}f = 1}} \ \underbracket[0pt]{g(\vec{v}) = \frac{\vec{v}-F(\vec{v})}{|\vec{v}-F(\vec{v})|},}_{\substack{{}\\[1mm] \text{jak wyżej}}} \ \underbracket[0pt]{h(\vec{v}) = - \frac{F(\vec{0})}{|F(\vec{0})|}.}_{\substack{{}\\[1mm] \text{stała jak w~przykładzie 2,} \\ \operatorname{ind}h = 0}}\] Naszym celem jest wykazanie, że krzywa \(f\) jest homotopijna z \(g,\) a \(g\) z \(h.\) Z wniosku 4 wyniknie wtedy, że indeksy krzywych \(f,\) \(g\) i \(h\) są równe – choć dobrze wiemy, że indeks \(f\) wynosi \(1,\) a indeks \(h\) to \(0.\) Ta oczywista sprzeczność pokazuje, że gdzieś musiał być błąd, i tym błędem musiało być początkowe założenie, że ,,\(F\) nie ma punktu stałego”. Skoro tak, to szukany przez nas punkt istnieje i dowód jest zakończony. ◻
Pozostaje więc dowieść homotopijności \(f,\) \(g\) i \(h,\) co naturalnie dzieli się na dwa kroki:
Dowód, że \(f\) i \(g\) są homotopijne. Rozważmy homotopię daną wzorem: \[H(t,\vec{v}) := \frac{\vec{v}-tF(\vec{v})}{|\vec{v}-tF(\vec{v})|}, \ \ \ \vec{v}\in \mathbb{S}_1, \ \ \ 0 \leq t \leq 1.\] Jest to przekształcenie dobrze określone i ciągłe, ponieważ unikamy dzielenia przez zero: \(|\vec{v}-tF(\vec{v})| \neq 0\) dla wszystkich \(\vec{v}\in {\mathbb{D}}\) i \(t \in [0,1].\) Istotnie, dla \(t = 1\) jest to konsekwencja naszego założenia \(F(\vec{v}) \neq \vec{v},\) natomiast dla \(t < 1\) punkt \(t F(\vec{v})\) leży ściśle wewnątrz okręgu jednostkowego (wszak \(|F(\vec{v})| \le 1\)), co w szczególności oznacza \(t F(\vec{v}) \neq \vec{v}.\)
Co więcej, \(H(0,\vec{v}) = f(\vec{v})\) (tu warto przypomnieć, że \(|\vec{v}|=1\)) oraz \(H(1,\vec{v}) = g(\vec{v}).\) Przekształcenie \(H\) jest więc homotopią w sensie wniosku 4. ◻
Dowód, że \(g\) i \(h\) są homotopijne. Tym razem przyjmijmy: \[H(t,\vec{v}) := \frac{t\vec{v}-F(t\vec{v})}{|t\vec{v}-F(t\vec{v})|}, \ \ \ \vec{v}\in \mathbb{S}_1, \ \ \ 0 \leq t \leq 1.\] Wówczas łatwo zauważyć, że:
\(H\) jest dobrze określone i ciągłe, bo nie dzielimy przez zero;
\(H(1,\vec{v}) = g(\vec{v})\);
\(H(0,\vec{v}) = h(\vec{v}).\)
Tak więc \(H\) w ciągły sposób przekształca \(g\) w \(h.\) ◻
Uwagi końcowe
Ograniczyliśmy się do rozważania dwuwymiarowego koła \({\mathbb{D}},\) którego brzegiem jest jednowymiarowy okrąg \(\mathbb{S},\) ale jedynie dlatego, że łatwo jest określić indeks krzywej w okręgu. To samo rozumowanie przenosi się jednak na kule wymiaru \(3\) i wyżej, wystarczy w tym celu pojęcie indeksu krzywej zamienić na ogólniejsze pojęcie stopnia przekształcenia. Istnieją nawet nieskończenie wymiarowe wersje twierdzenia Brouwera, przydatne w teorii równań różniczkowych cząstkowych. Teoria stopnia przekształcenia, lub ogólniej teoria grup homotopii, stanowi natomiast jedno z podstawowych zagadnień dziedziny znanej jako topologia algebraiczna.
Na koniec odnotujmy ważną własność przedstawionego przez nas dowodu twierdzenia Brouwera: nie mamy żadnego pojęcia, gdzie jest szukany punkt stały. Dowód nie jest konstruktywny – nie daje nam żadnej wskazówki, gdzie szukać. Wiemy tylko tyle, że istnieje. Co więcej, nie jest on wyznaczony jednoznacznie – punktów stałych może być wiele, choćby dla przekształcenia identycznościowego, czyli kiedy kawy wcale nie zamieszaliśmy. Na sam koniec, jako ostatnie ćwiczenie, zachęcam Czytelnika do samodzielnego sformułowania i dowodu twierdzenia Brouwera w przypadku jednowymiarowym, w którym rolę koła jednostkowego spełnia odcinek \([-1,1].\)
Konstruktywny dowód twierdzenia Brouwera przedstawił Jarosław Górnicki w \(\Delta^{7}_{20}\). Wyprowadzenie tego wyniku z twierdzenia Borsuka–Ulama można za to znaleźć u Krzysztofa Ciesielskiego i Zdzisława Pogody w \(\Delta^{11}_{99}\).