Delta 9/2024

Klub 44

Marcin E. Kuczma i Elżbieta Zawistowska

Zadania z matematyki nr 885, 886

Redaguje Marcin E. KUCZMA

885. Niech $p$ będzie ustaloną liczbą pierwszą nieparzystą i niech $M = {1, 2, \dots, p - 1} .$ Wyznaczyć liczbę funkcji $f : M \to M$ takich, że dla każdego $x \in M$ liczba $x f (f (x)) - 1$ dzieli się przez $p .$

886. W trójkącie ostrokątnym o bokach długości $a, b, c$ kąty wewnętrzne przy przeciwległych wierzchołkach mają miary (odpowiednio) $α, β, γ .$ Wykazać, że wartość ilorazu $\frac{a \cos α + b \cos β + c \cos γ}{a + b + c}$ wyraża się przez długości promieni okręgów opisanego i wpisanego. Wyjaśnić, czy uzyskany wzór jest słuszny również dla trójkątów rozwartokątnych.

Zadanie 886 zaproponował pan Marian Łupieżowiec z Gliwic.

Rozwiązania zadań z numeru 5/2024

Przypominamy treść zadań:

881. Ciąg $a_{0}, a_{1}, a_{2}, \dots$ jest określony wzorami: $a_{0} = 3,$ $a_{n + 1} = a_{n}^{2} - 2 .$ Obliczyć granicę $lim_{n \to \infty} \frac{1}{a_{n}} \prod_{i = 0}^{n - 1} a_{i}$ lub wykazać, że ta granica nie istnieje.

Rozwiązanie

Należy zbadać granicę ciągu $(b_{n} / a_{n}),$ gdzie $b_{n} = a_{0} \dots a_{n - 1}$ (przyjmujemy $b_{0} = 1$ ). Widać, że $b_{n + 1} = a_{n} b_{n} .$ Wykażemy indukcyjnie, że dla $n = 0, 1, 2, \dots$ zachodzi równość $a_{n}^{2} - 5 b_{n}^{2} = 4.$ Dla $n = 0$ zgadza się. Przyjmijmy słuszność wzoru dla $n$ i przejdźmy do $n + 1$ : $a_{n + 1}^{2} - 5 b_{n + 1}^{2} = (a_{n}^{2} - 2)^{2} - 5 (a_{n} b_{n})^{2} = a_{n}^{2} (a_{n}^{2} - 4 - 5 b_{n}^{2}) + 4 = 4;$ w ostatnim kroku użyte zostało założenie indukcyjne (wyrażenie w nawiasie zeruje się). Dowodzona równość zachodzi więc dla wszystkich $n \geq 0 .$ Wynika z niej, że $(\frac{b_{n}}{a_{n}})^{2} = \frac{a_{n}^{2} - 4}{5 a_{n}^{2}} = \frac{1}{5} (1 - \frac{4}{a_{n}^{2}}) .$ Jasne, że $a_{n} \to \infty .$ Stąd $lim_{n \to \infty} (\frac{b_{n}}{a_{n}})^{2} = \frac{1}{5}, zatem lim_{n \to \infty} \frac{b_{n}}{a_{n}} = \frac{1}{\sqrt{5}} .$

882. Na bokach $A B,$ $B C,$ $C D,$ $D A$ równoległoboku $A B C D$ wybrano, odpowiednio, punkty $K, L, M, N,$ różne od wierzchołków. Weźmy pod uwagę trójkąty $A N K,$ $B K L,$ $C L M,$ $D M N .$ Udowodnić, że każda z następujących czwórek punktów stanowi czwórkę wierzchołków pewnego równoległoboku: (a) ortocentra tych trójkątów; (b) środki ciężkości tych trójkątów; (c) środki okręgów opisanych na tych trójkątach.

Rozwiązanie

Oznaczmy ortocentra tych czterech trójkątów, w podanej kolejności, przez $H_{a}, H_{b}, H_{c}, H_{d}$ ; ich środki ciężkości – przez $G_{a}, G_{b}, G_{c}, G_{d}$ ; zaś środki okręgów na nich opisanych – przez $O_{a}, O_{b}, O_{c}, O_{d} .$

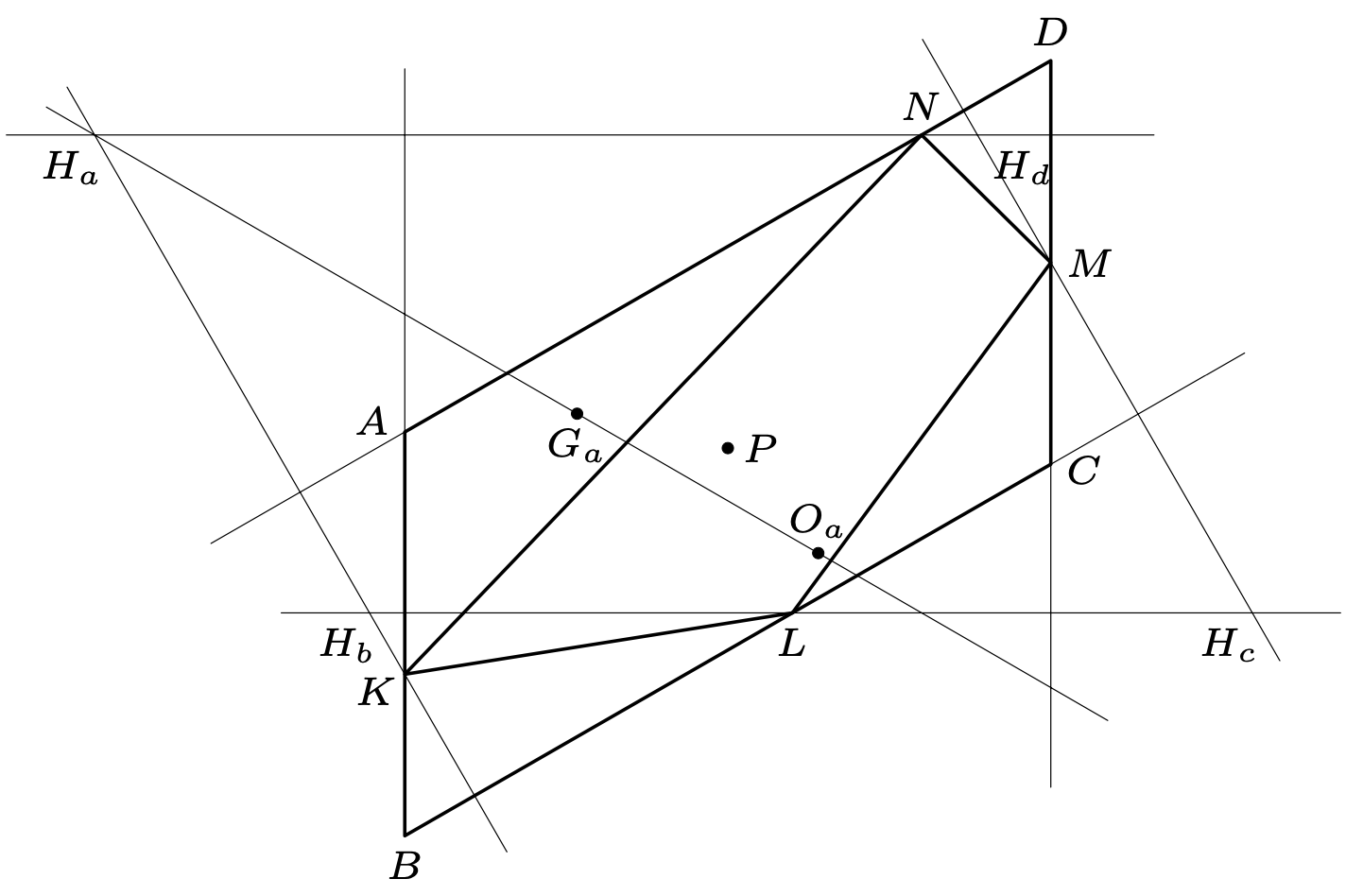
(a) Punkty $H_{a}$ i $H_{b}$ leżą na prostej przechodzącej przez $K$ (wspólny wierzchołek trójkątów $A N K,$ $B K L$ ), prostopadłej do prostych $D A$ i $B C .$ Punkty $H_{c}$ i $H_{d}$ leżą na prostej przechodzącej przez $M$ i także prostopadłej do $D A$ i $B C .$ Zatem $H_{a} H_{b} ‖ H_{c} H_{d} .$ Analogicznie pokazujemy, że $H_{b} H_{c} ‖ H_{d} H_{a}$ : czworokąt $H_{a} H_{b} H_{c} H_{d}$ jest równoległobokiem.

(b) Rachujemy na wektorach. Niech $P$ będzie punktem przecięcia przekątnych $A C$ i $B D$ ; a więc $\vec{P A} + \vec{P C} = \vec{0} = \vec{P B} + \vec{P D} .$ Stąd $\begin{aligned} \vec{P G_{a}} + \vec{P G_{c}} & = \frac{1}{3} (\vec{P A} + \vec{P N} + \vec{P K}) + \frac{1}{3} (\vec{P C} + \vec{P L} + \vec{P M}) = \\ = \frac{1}{3} (\vec{P N} + \vec{P K} + \vec{P L} + \vec{P M}), \\ \vec{P G_{b}} + \vec{P G_{d}} & = \frac{1}{3} (\vec{P B} + \vec{P K} + \vec{P L}) + \frac{1}{3} (\vec{P D} + \vec{P M} + \vec{P N}) = \\ = \frac{1}{3} (\vec{P K} + \vec{P L} + \vec{P M} + \vec{P N}) . \end{aligned}$ Uzyskana równość $\begin{matrix} (1) & \vec{P G_{a}} + \vec{P G_{c}} = \vec{P G_{b}} + \vec{P G_{d}} \end{matrix}$ oznacza, że środki odcinków $G_{a} G_{c}$ i $G_{b} G_{d}$ pokrywają się: czworokąt $G_{a} G_{b} G_{c} G_{d}$ jest równoległobokiem.

(c) W trójkącie $A N K$ (jak w każdym trójkącie) rozważane punkty charakterystyczne $O_{a},$ $G_{a},$ $H_{a}$ leżą w tej kolejności na jednej prostej (Eulera), tworząc proporcję $O_{a} G_{a} : G_{a} H_{a} = 1 : 2 .$ Stąd $\vec{P G_{a}} = \frac{2}{3} \vec{P O_{a}} + \frac{1}{3} \vec{P H_{a}},$ czyli $\vec{P O_{a}} = \frac{3}{2} \vec{P G_{a}} - \frac{1}{2} \vec{P H_{a}} .$ Analogicznie wyrażają się wektory $\vec{P O_{b}}, \vec{P O_{c}}, \vec{P O_{d}} .$

Z konkluzji części (a) wynika, że odcinki $H_{a} H_{c}$ i $H_{b} H_{d}$ mają wspólny środek, czyli że $\begin{matrix} (2) & \vec{P H_{a}} + \vec{P H_{c}} = \vec{P H_{b}} + \vec{P H_{d}} . \end{matrix}$ Skoro zaś (dla $x = a, b, c, d$ ) wektory $\vec{P O_{x}}$ wyrażają się jednolitym wzorem jako kombinacja liniowa wektorów $\vec{P G_{x}}, \vec{P H_{x}},$ z równości (1) i (2) wynika taka sama równość dla wektorów $\vec{P O_{x}}$ : $\vec{P O_{a}} + \vec{P O_{c}} = \vec{P O_{b}} + \vec{P O_{d}} .$ Oznacza ona, że odcinki $O_{a} O_{c}$ i $O_{b} O_{d}$ mają wspólny środek: czworokąt $O_{a} O_{b} O_{c} O_{d}$ jest równoległobokiem.

Zadania z fizyki nr 782, 783

Redaguje Elżbieta ZAWISTOWSKA

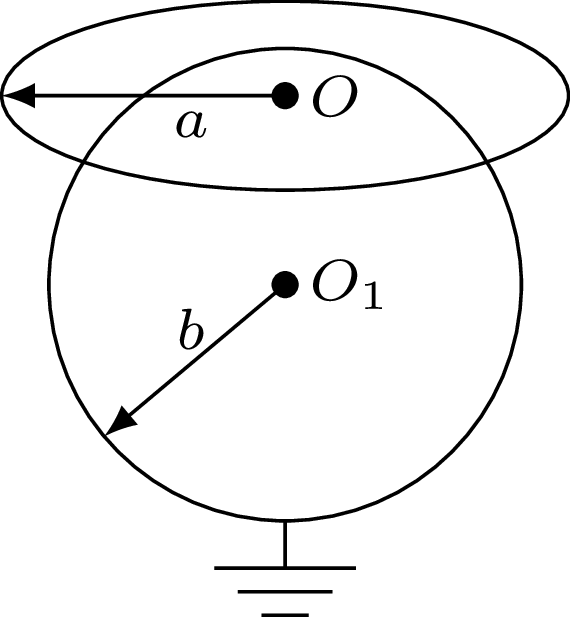
782. Potencjał w środku odosobnionego, naładowanego, drucianego pierścienia o promieniu $a$ wynosi $φ_{a} .$ Pierścień ten zbliżono do uziemionej przewodzącej sfery o promieniu $b$ tak, że tylko środek pierścienia znajduje się na powierzchni sfery (rys. 1). Znaleźć ładunek indukowany na sferze.

783. Mała kulka o masie $m$ naładowana ładunkiem $q$ zawieszona jest na nieważkiej i nierozciągliwej nici w jednorodnym polu magnetycznym o indukcji $B_{0}$ skierowanej pionowo. Kulkę odchylono o mały kąt z położenia równowagi i puszczono swobodnie. Po jakim czasie płaszczyzna wahań wahadła obróci się o kąt $2 π$ ? Maksymalna siła Lorentza działająca na kulkę jest mała w porównaniu z maksymalną siłą zawracającą. Nie uwzględniamy efektów związanych z obrotem Ziemi.

Rozwiązania zadań z numeru 5/2024

Przypominamy treść zadań:

778. Na osi długiej rury o lustrzanej powierzchni wewnętrznej znajduje się punktowe, izotropowe źródło światła oraz całkowicie pochłaniająca światło kulka o promieniu $r = 1$ cm. Środek kulki znajduje się w odległości $l = 2$ cm od źródła. Jaki powinien być promień wewnętrzny rury, aby kulka pochłaniała połowę energii emitowanej przez źródło?

Rozwiązanie

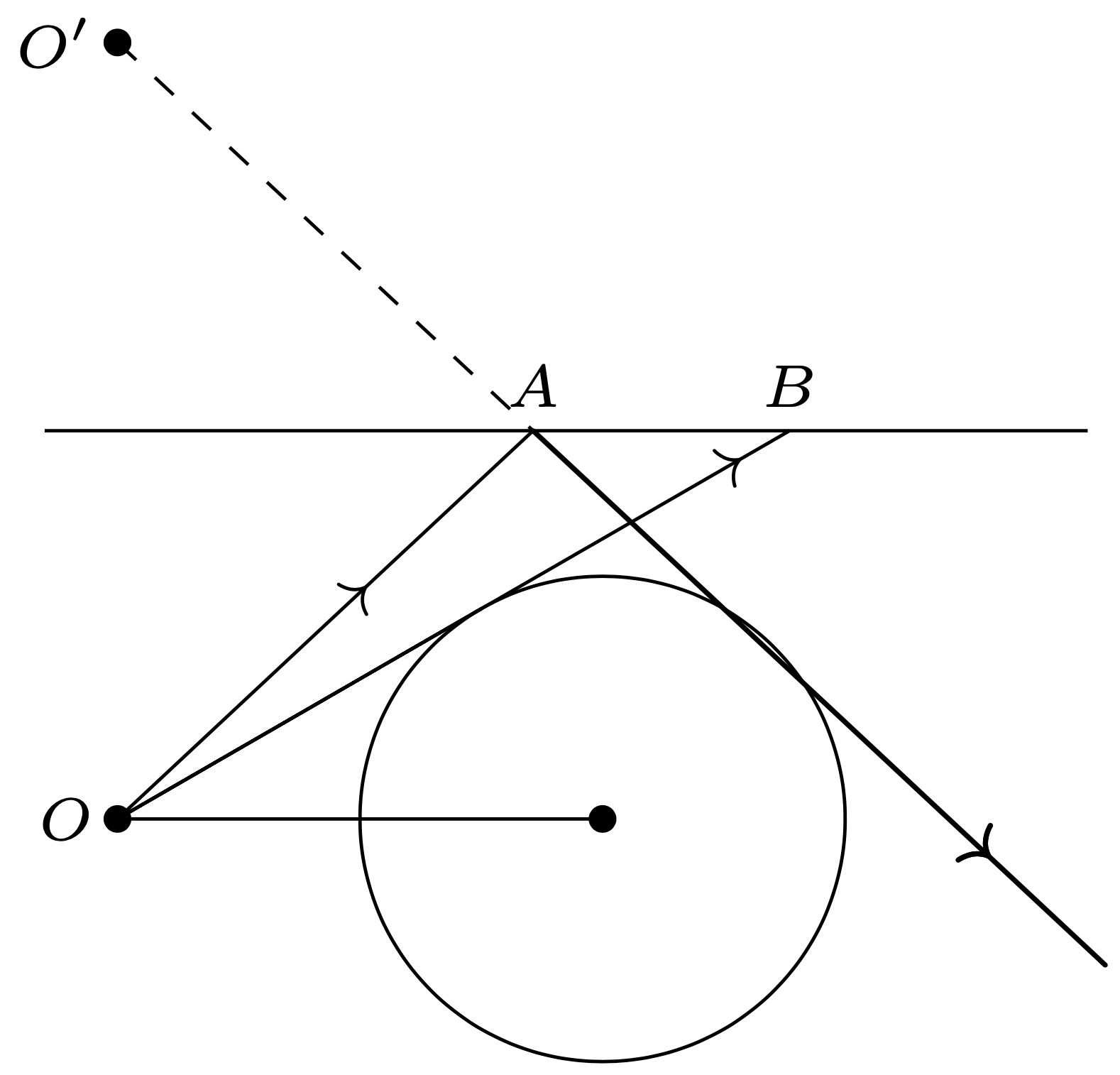
Rys. 2 Rysunek 2 przedstawia bieg promieni wychodzących ze źródła $O,$ w płaszczyźnie przekroju rury. Promienie w obszarze $O A B$ nie spełniają warunków zadania. Zmniejszając promień rury, zmniejszamy powierzchnię tego obszaru. Przypadek graniczny, gdy wszystkie promienie biegnące ze źródła na prawo od prostej $O O^{'},$ wyznaczonej przez źródło i jego obraz, trafiają na kulkę bezpośrednio albo po odbiciach od powierzchni wewnętrznej rury, przedstawia rysunek 3.
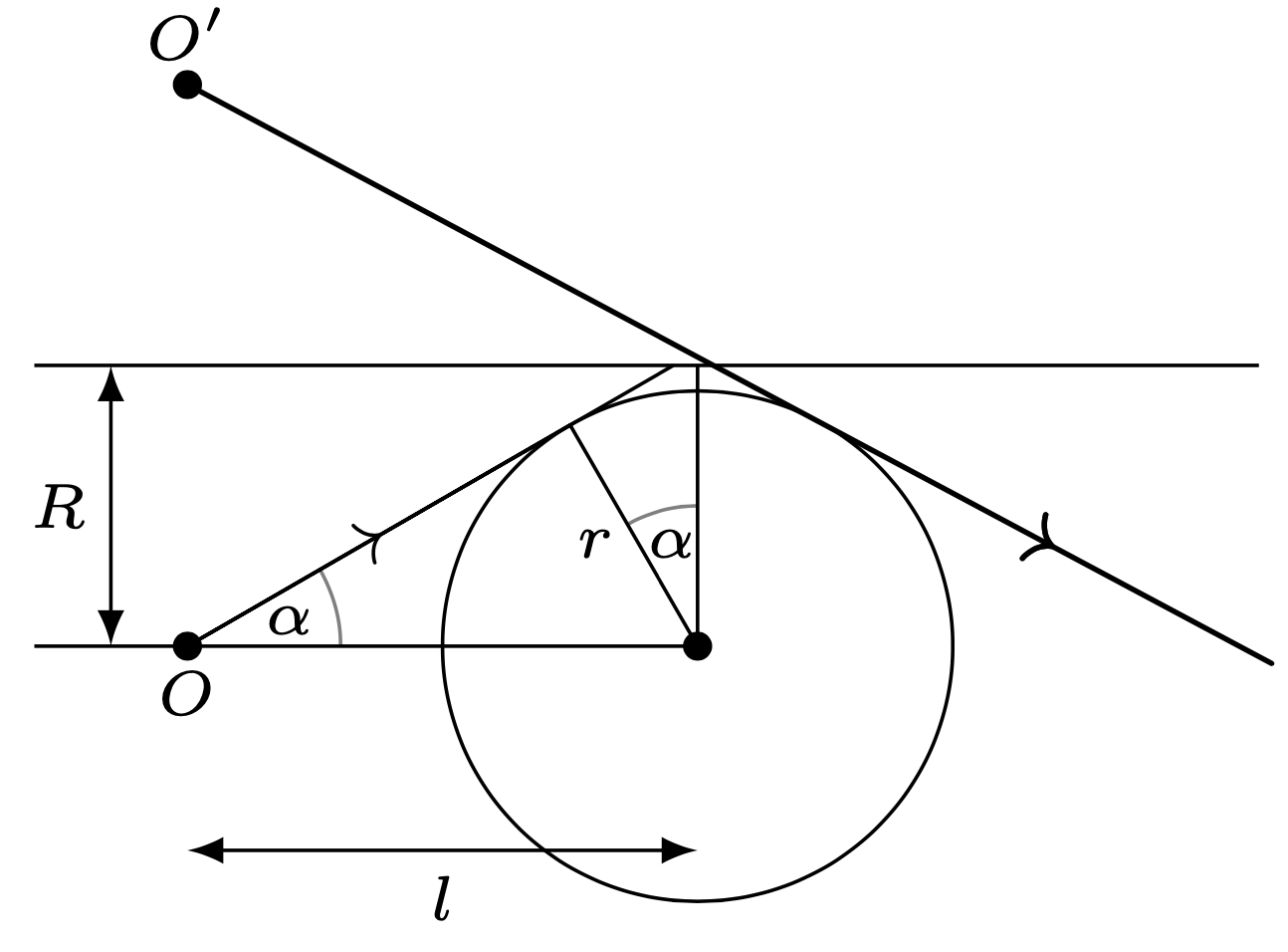
Rys. 3 Promienie biegnące w lewo od prostej $O O^{'}$ wychodzą z rury albo bezpośrednio, albo po wielokrotnych odbiciach.

Maksymalny promień rury, dla którego spełnione są warunki zadania, dany jest wzorem: $R = r / \cos α = r / \sqrt{1 - r^{2} / l^{2}} \approx 1, 15 c m .$

779. W pionowo ustawionym naczyniu, pod ciężkim tłokiem znajduje się niewielka ilość helu. Nie ma ciśnienia atmosferycznego, tłok „wisi” na wysokości $H$ nad dnem naczynia, a jego tarcie o ścianki naczynia jest zaniedbywalne. Tłok bardzo szybko podniesiono na wysokość $10 H$ względem dna naczynia (tak, że podczas podnoszenia nie dochodziło do zderzeń z cząsteczkami gazu) i po ustaleniu się równowagi puszczono swobodnie. Na jakiej wysokości nad dnem naczynia tłok zatrzymał się, gdy ustały jego drgania? Naczynie nie przewodzi ciepła, pojemność cieplną ścianek i tłoka można zaniedbać, hel traktujemy jako gaz doskonały.

Rozwiązanie

Podczas podnoszenia tłoka nie jest wykonywana praca nad gazem, nie ma wymiany ciepła z otoczeniem i gaz jest doskonały, zatem zgodnie z pierwszą zasadą termodynamiki energia wewnętrzna gazu nie zmienia się: $Δ U = n c_{V} (T_{1} - T_{0}) = 0,$ a tym samym w wyniku podniesienia tłoka nie zmienia się jego temperatura: $T_{1} = T_{0} .$

Podczas opadania tłoka praca wykonana nad gazem wynosi $W = M g (10 H - x),$ gdzie $M$ jest masą tłoka, a $x$ szukaną wysokością końcową. Zasada zachowania energii ma postać: $\begin{matrix} (1) & M g (10 H - x) = 3 n R (T_{2} - T_{0}) / 2. \end{matrix}$ Ciśnienia w stanach początkowym i końcowym są jednakowe: $p_{2} = M g / S = p_{0},$ gdzie $S$ jest przekrojem naczynia. Z równań Clapeyrona : $p_{0} S H = n R T_{0}$ , $p_{2} S x = n R T_{2},$ otrzymujemy: $\begin{matrix} (2) & T_{2} = T_{0} x / H . \end{matrix}$ Wstawiając $(2)$ do $(1)$ , dostajemy: $x = 4, 6 H .$

Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
875 ( $W T = 2, 62$ ) i 876 ( $W T = 1, 48$ )
z numeru 2/2024

Łukasz Merta Kraków 42,56

Piotr Kumor Olsztyn 41,92

Szymon Kitowski 41,11

Adam Woryna Ruda Śl. 40,91

Witold Bednarek Łódź 37,29

Krzysztof Zygan Lubin 34,43

Michał Adamaszek Kopenhaga 31,25

Jędrzej Biedrzycki 31,02

Andrzej Kurach Ryjewo 30,66

Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
772 ( $W T = 1, 64$ ), 773 ( $W T = 2, 71$ ) z numeru 1/2024

Ryszard Baniewicz Włocławek 2–44+0,43

Jacek Konieczny Poznań 40,41

Konrad Kapcia Poznań 2–39,58

Paweł Perkowski Ożarów Maz. 5–35,07

Andrzej

Nowogrodzki Chocianów 3–23,69

Jan Zambrzycki Białystok 4–22,38

Tomasz Wietecha Tarnów 17–20,53

Paweł Kubit Kraków 17,21

Łukasz Merta	Kraków	42,56
Piotr Kumor	Olsztyn	41,92
Szymon Kitowski		41,11
Adam Woryna	Ruda Śl.	40,91
Witold Bednarek	Łódź	37,29
Krzysztof Zygan	Lubin	34,43
Michał Adamaszek	Kopenhaga	31,25
Jędrzej Biedrzycki		31,02
Andrzej Kurach	Ryjewo	30,66

Ryszard Baniewicz	Włocławek	2–44+0,43
Jacek Konieczny	Poznań	40,41
Konrad Kapcia	Poznań	2–39,58
Paweł Perkowski	Ożarów Maz.	5–35,07
Andrzej
Nowogrodzki	Chocianów	3–23,69
Jan Zambrzycki	Białystok	4–22,38
Tomasz Wietecha	Tarnów	17–20,53
Paweł Kubit	Kraków	17,21