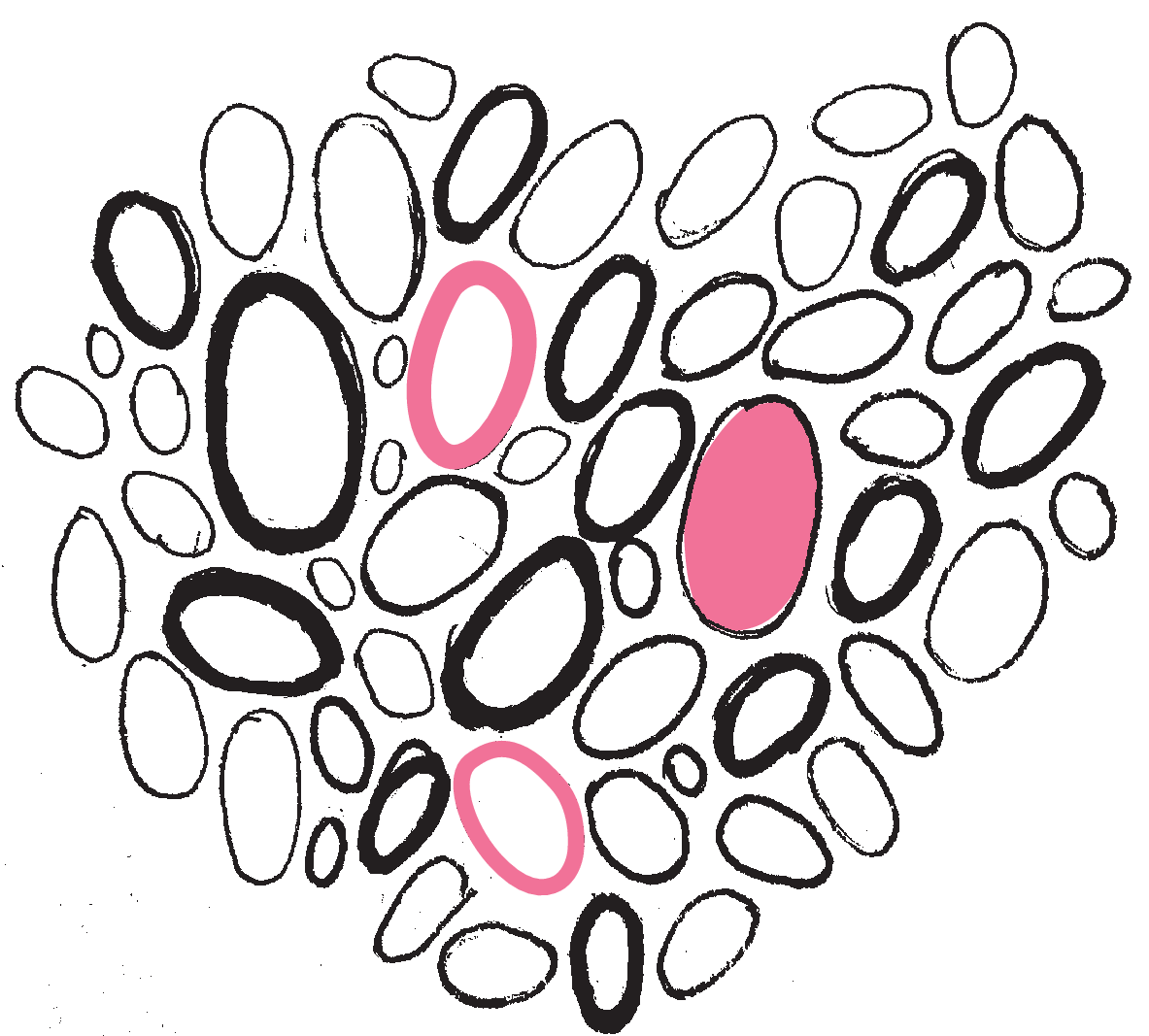Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Tytułowe pytanie może brzmieć dosyć dziwnie. Płaszczyzna jest nieskończona, więc i liter na niej możemy napisać nieskończenie wiele (dysponując, jak to matematycy, nieskończonym czasem). Nie od dziś wiadomo jednak, że nieskończoności są różne, jedne mniejsze, drugie większe. Która z tych nieskończoności odpowiada na tytułowe pytanie? I czy zależy to od litery, której ono dotyczy? Nad tym właśnie zastanowimy się w niniejszym artykule.
Czytelnikom, którym obce jest rozróżnianie między nieskończonościami, polecamy Deltowy wykład na ich temat autorstwa Michała Korcha, zwłaszcza odcinek Nieskończoność 4. Nie każda jest taka sama, \(\Delta^{6}_{19}.\) Poniżej w pigułce prezentuję istotne dla nas wiadomości – dla tych, którzy potrzebują jedynie krótkiego przypomnienia w tym zakresie. Powiemy, że dwa zbiory są równoliczne, jeśli ich elementy można ,,połączyć w pary”, czyli jeśli istnieje między nimi bijekcja. Równoliczne są zatem zbiory liczb naturalnych i liczb parzystych, a odpowiednia bijekcja między tymi zbiorami to funkcja \(f(n)=2n.\) Każdy zbiór, który jest równoliczny ze zbiorem liczb naturalnych, nosi nazwę przeliczalnego. Przeliczalne są wszystkie nieskończone podzbiory zbioru liczb naturalnych, jak również pewne jego nadzbiory (np. zbiór liczb wymiernych). Przeliczalne są również zbiory par, trójek, czwórek itp. elementów pochodzących ze zbioru przeliczalnego (np. przeliczalny jest zbiór par liczb naturalnych, co mocno wiąże się z przeliczalnością zbioru liczb wymiernych). Przykładem zbioru nieprzeliczalnego jest zbiór liczb rzeczywistych, a nawet sam odcinek \([0,1].\) Jego ,,liczba elementów” nosi nazwę continuum; jest to również liczba punktów na płaszczyźnie czy w przestrzeni.
Wracając do tytułowego problemu, zaznaczmy od razu, że nie chcemy, aby litery się przecinały. Za przecinające się literki już w przedszkolu można było dostać deszczową chmurkę zamiast uśmiechniętego słoneczka, czego oczywiście chcemy uniknąć. Weźmy na warsztat najprostszą w zapisie literę, czyli \(\textsf{I}\). Czy na płaszczyźnie starczy miejsca na continuum egzemplarzy, czy ,,tylko” przeliczalnie wiele? Okazuje się, że \(\textsf{I}\) specjalnie się nie rozpycha, i możemy upakować jej continuum. Wystarczy dla każdej liczby rzeczywistej \(t\) narysować kreskę od punktu \((t,0)\) do punktu \((t,1).\) Każda taka kreska (przyznajmy, zerowej grubości) może śmiało reprezentować literę \(\textsf{I}\), i postawiliśmy ich continuum (rys. 1). Na więcej nie mamy co liczyć, gdyż na płaszczyźnie jest tylko (aż?) continuum punktów.
Rys. 1. Continuum liter \(\textsf{I}\) na płaszczyźnie, na czarno zaznaczono jedną z nich
To, co zadecydowało o sukcesie całej operacji, to możliwość przesuwania
\(\textsf{I}\) w ustalonym kierunku tak, by żadna z przesuniętych wersji nie
zahaczała o pozostałe. To samo moglibyśmy wykonać w przypadku \(\textsf{N}\)
(rys. 2), \(\textsf{Z}\), \(\textsf{M}\) czy \(\textsf{W}.\)
Dla każdej z tych liter możemy bowiem wskazać kierunek taki, że każda prosta
w tym kierunku przecina naszą literę co najwyżej raz. Niektórzy matematycy,
zwani topologami, mogliby w tym momencie uśmiechnąć się z politowaniem, ponieważ dla
nich wszystkie te litery są niejako tożsame z \(\textsf{I}\), gdyż są po prostu jej
powyginanymi wersjami, i wniosek co do liczności możliwych
do upchania egzemplarzy powinien być ten sam.
Cóż, gdyby, mając napisać na kartce \(\textsf{N}\), nabazgrali
, to od razu zobaczyliby w zeszycie burzowe chmurzysko, i mina by im zrzedła. My
będziemy staranni!
Rys. 2. Continuum liter \(\textsf{N}\) na płaszczyźnie. Literę trzeba przesuwać ,,pod kątem”, by uniknąć nachodzenia na siebie
Można w tym momencie nabrać podejrzeń, że każdą literę możemy napisać na płaszczyźnie continuum razy. Przyjrzyjmy się jednak literze \(\textsf{O}\). Tutaj przesuwanie już nie zadziała – niewielkie przesunięcia skutkują przecięciami, obojętnie w jakim kierunku zostaną wykonane. Możemy jednak powiększać tę literę niczym pompowany balonik. Dostaniemy wówczas koncentryczne okręgi o różnych promieniach (rys. 3). Ponieważ promień możemy wybrać dowolny, liter \(\textsf{O}\) również możemy zmieścić continuum.
Rys. 3. Continuum liter \(\textsf{O}\) na płaszczyźnie
Takie rozwiązanie może się jednak nie podobać. Mało który przedszkolak poproszony o napisanie na kartce kilku liter \(\textsf{O}\) umieściłby pewne dwie jedna wewnątrz drugiej. Możemy zatem w tym wypadku chcieć nie tylko, by litery się nie przecinały, lecz również by rozłączne były zamknięte przez nie obszary płaszczyzny. Gdy dołożymy takie wymaganie, odpowiedź na nasze pytanie ulegnie zmianie. Zauważmy bowiem, że wewnątrz każdej litery \(\textsf{O}\) na płaszczyźnie musi się znaleźć punkt o współrzędnych wymiernych, niezależnie od tego, jak koślawo ją napiszemy. Jest to konsekwencja faktu, że między dowolnymi dwiema różnymi liczbami rzeczywistymi znajduje się liczba wymierna. Punkty przypisane różnym literom muszą być różne, skoro ich wnętrza są rozłączne. Ponieważ liczb wymiernych jest przeliczalnie wiele, tyle jest również ich par, czyli punktów o współrzędnych wymiernych. Dowodzi to, że liter \(\textsf{O}\) o rozłącznych wnętrzach można umieścić na płaszczyźnie tylko przeliczalnie wiele. To samo tyczy się wszystkich liter ,,zamykających” jakiś fragment płaszczyzny: \(\textsf{A}\), \(\textsf{B}\), \(\textsf{P}\) czy \(\textsf{R}\).
Spróbujmy teraz naszych sił z literą \(\textsf{Y}\). Wydaje się, że nie zajmuje ona zbyt wiele miejsca – przede wszystkim nie ma żadnego ,,brzuszka”, więc nie jesteśmy w stanie, używając poprzedniego argumentu, uzasadnić, że zmieści się tylko przeliczalnie wiele jej egzemplarzy. Można powiedzieć, że składa się ona z trzech połączonych liter \(\textsf{I}\), co pozwala nabrać podejrzeń, że na płaszczyźnie znajdzie się miejsce na ich continuum. Jednak podstawowe zastosowane dotychczas sztuczki w tym wypadku się nie sprawdzają – zarówno przesuwanie, jak i skalowanie (które działało w przypadku litery \(\textsf{O}\)) nie dają pożądanego rezultatu. Intuicja może podpowiadać, że odpowiednio ją wyginając (nawet kosztem niskich not za styl), będziemy na tyle blisko litery \(\textsf{I}\), że kontinuum powinno być w zasięgu ręki. Ta intuicja jest jednak błędna, o czym przekonuje poniższe rozumowanie.
Rozważmy zatem dowolny zbiór nieprzecinających się liter \(\textsf{Y}\) na płaszczyźnie. Udowodnimy, że musi on być co najwyżej przeliczalny. Dla ułatwienia dalszego rozumowania, wprowadźmy pojęcie koła wymiernego, to znaczy takiego, że zarówno jego promień, jak i obie współrzędne środka są wymierne. Wymiernych kół jest zatem przeliczalnie wiele, podobnie jak ich par, trójek, czwórek itp.
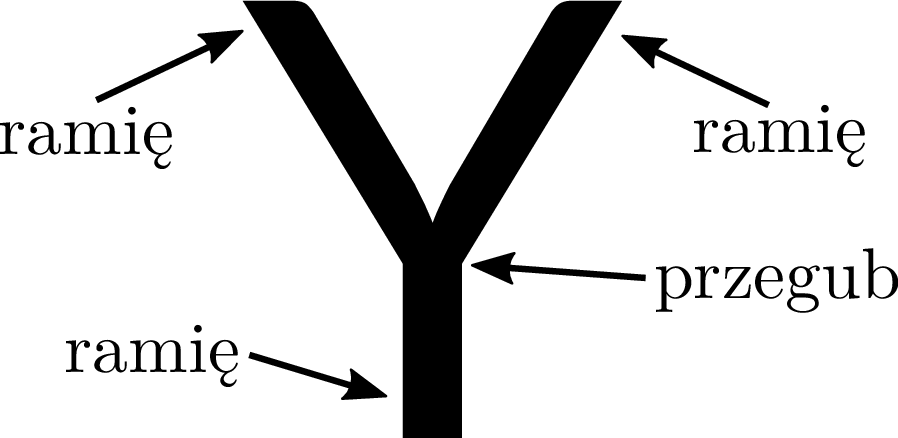
Przyjrzyjmy się teraz igrekowej anatomii. Litera \(\textsf{Y}\) ma trzy ramiona łączące się w punkcie, który nazwiemy przegubem (rys. 4). Jakbyśmy takiej litery \(\textsf{Y}\) nie napisali, możemy wskazać trzy rozłączne i wymierne koła, z których każde
Rys. 4. Anatomia litery \(\textsf{Y}\)
zawiera koniec jednego z jej ramion,
nie przecina żadnego z pozostałych ramion, w szczególności nie zawiera przegubu.
Każdej napisanej przez nas literze \(\textsf{Y}\) przypisujemy w ten sposób trójkę wymiernych kół. Jak już wspomnieliśmy, takich trójek jest przeliczalnie wiele. To oczywiście nie koniec dowodu – dwie litery \(\textsf{Y}\) mogą mieć przypisany ten sam zestaw trzech wymiernych kół, jak pokazuje rys. 5. Okazuje się jednak, że jeden zestaw nie może być współdzielony przez trzy litery \(\textsf{Y}\). Stwierdzenie to, które zaraz uzasadnimy, implikuje, że liter \(\textsf{Y}\) napisaliśmy co najwyżej przeliczalnie wiele.
Rys. 5. Dwie malownicze litery \(\textsf{Y}\), którym przypisaliśmy tę samą trójkę kół
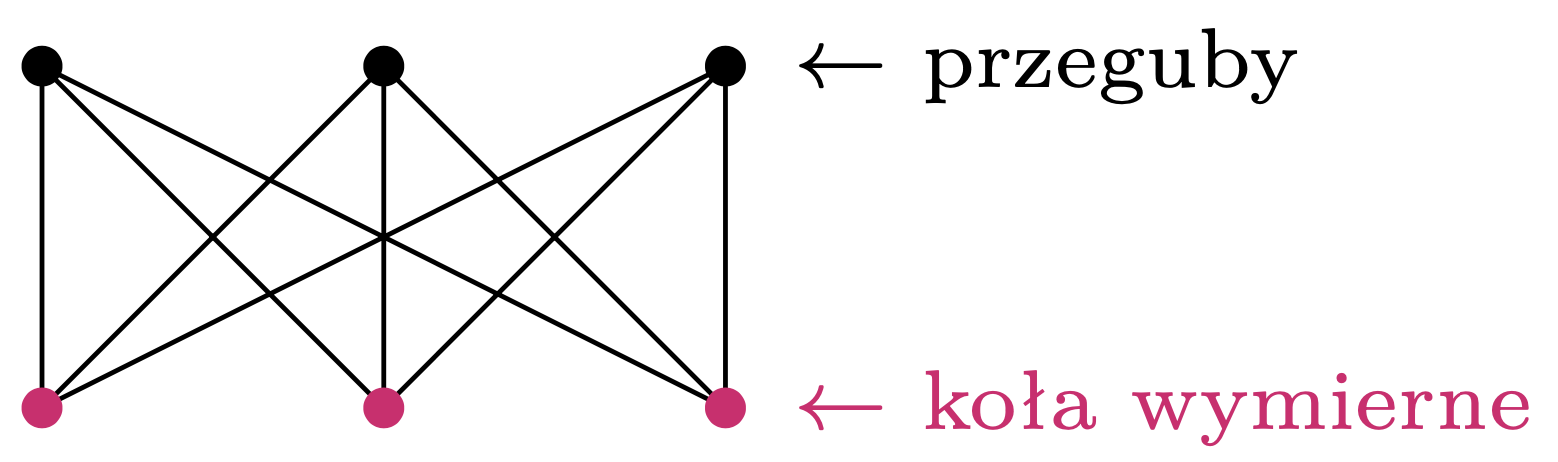
Rys. 6. Pełny graf dwudzielny \(K_{3,3},\) którego nie można narysować na kartce tak, by połączenia między wierzchołkami nie przecinały się
Przypuśćmy zatem, że jest inaczej – i że pewnym trzem literom \(\textsf{Y}\) przyporządkowaliśmy tę samą trójkę kół wymiernych. Mamy trzy koła wymierne i trzy przeguby, każdy przegub jest połączony kreską z każdym kołem wymiernym i kreski te nie przecinają się (bo nie przecinają się napisane przez nas litery \(\textsf{Y}\)). Polecam Czytelnikowi choć jedną próbę narysowania takiej konfiguracji. Nie udało się, prawda? I nie bez powodu – jest to niemożliwe! Problem ten przybiera różne postaci, w jednej z nich należy trzy domy podłączyć do źródeł wody, elektryczności i gazu tak, aby przyłącza nie przecinały się. A w formalnym żargonie jest to stwierdzenie nieplanarności pełnego grafu dwudzielnego \(K_{3,3}\) (rys. 6). Nie da rady i już – krótkie wyjaśnienie oparte na wzorze Eulera można odnaleźć w Deltoidzie z \(\Delta^{8}_{11}\).
Rys. 7. Litera \(\textsf{Y}\) (na czarno) jako podlitera innych liter
Ponieważ \(\textsf{Y}\) może zmieścić się na płaszczyźnie co najwyżej przeliczalnie wiele razy, to to samo dotyczy wszystkich liter, które zawierają \(\textsf{Y}\) jako ,,podliterę”. Przykładami są \(\textsf{T}\) czy \(\textsf{K}\), lecz również wspomniane wcześniej \(\textsf{A}\) i \(\textsf{P}\) (rys. 7), i to nawet jeśli dopuścimy ,,zawieranie” liter jedna w drugiej. Czytelnikowi proponujemy rozstrzygnięcie tytułowego pytania dla każdej z pozostałych liter alfabetu. Nie trzeba dodawać, że próby praktyczne są skazane na niepowodzenie…