Afiliacja: Student Wydziału Fizyki Uniwersytetu Warszawskiego członek Klubu Naukowego Fenix
Jak rozwiązywać zadania z fizyki?
Podążając za myślą Jana Kalinowskiego – sprawdź wymiary! (zob. \(\Delta_{92}^{3})\), a następnie zredukuj problem do wielkości bezwymiarowych. Radzę się przy tym nie pomylić, bo po omyłce całe podejście będzie postrzegane jako przedawkowanie elegancji, które grozi uduszeniem krawatem.
Czy to wszystko?
Otóż nie! Wielkości bezwymiarowe okazują się niezwykle użyteczne np. przy analizowaniu równań różniczkowych. Jeśli przeprowadzimy procedurę ubezwymiarowienia takiego równania, to znaczy sprowadzimy je do wielkości o wymiarze (jednostce) 1, to dostaniemy równanie, które na przykład zależy od jednej bezwymiarowej wielkości. Będzie to ta sama stała, którą dostaniemy z analizy wymiarowej (z dokładnością do potęgi). Jak później zobaczymy, pozwala to na zrozumienie wpływu istotnych zjawisk na dynamikę wynikającą z równań.
Zatem procedura daje przyjemniejsze dla oka równanie, fizyczną intuicję stojącą za jego zachowaniem w zależności od parametru, który rozumiemy, możliwość rysowania krzywych skalowania, ang. master curves opisanych w Sprawdź wymiary!, a także wiele innych korzyści, których nie da się wyczerpująco opisać w jednym artykule.
Charakterystyczne wielkości.
Zacznijmy od pytania, jak mierzyć wielkości w układach fizycznych? Opisywanie odległości w metrach czy czasu w sekundach jest mało interesującym podejściem, gdyż przekazuje mało informacji. Więcej wniosków dostarczy nam przekazanie wartości w skali ważnej wielkości w układzie.
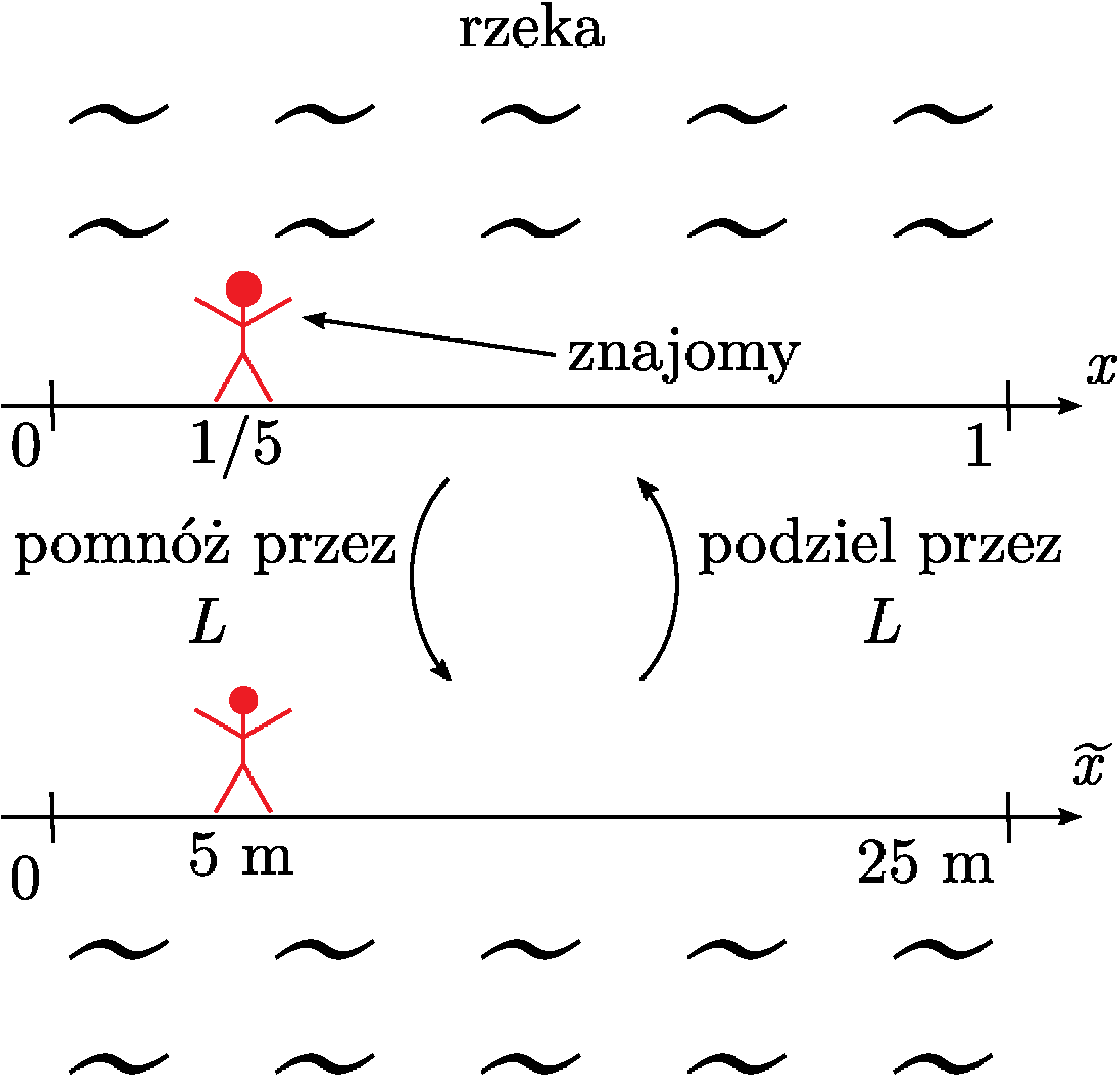
Przykład: Wyobraźmy sobie rozmowę przez telefon ze znajomym, który właśnie pokonuje rwącą rzekę. Możemy usłyszeć dwa stwierdzenia:
Przebyłem \(5\textrm{ m}\)!
Przebyłem \(1/5\) szerokości rzeki!
Rys. 1. Dwa podejścia do mierzenia położenia znajomego i przejście pomiędzy nimi przez dzielenie i mnożenie przez wielkość charakterystyczną
Pierwsze stwierdzenie dostarcza nam mało informacji na temat położenia znajomego, na podstawie drugiego możemy jednak dokładnie wyobrazić sobie odcinek odpowiadający szerokości rzeki (która jest nam nieznana) i naszego rozmówcę umiejscowionego na nim. Dla wygody wyobraźmy sobie, że odcinek ten ma długość 1, i oznaczmy na nim pozycję znajomego jako \(x\) (Uwaga! nasz \(x\) nie ma wymiaru). Gdybyśmy chcieli przejść do wielkości z wymiarem, wymnożymy wszystko przez szerokość rzeki \(L,\) tak jak na rysunku 1. Wtedy nasz wyobrażony odcinek zyskuje szerokość \(L,\) a rzeczywiste położenie, już w metrach, wynosi: \(\tilde{x}=x L.\)
W różnych układach charakterystyczne wymiary przyjmują różną postać, ale zawsze będzie ich co najmniej tyle, co trzeba. Często jednak jest ich za dużo, na przykład dwie charakterystyczne długości. Wtedy, zgodnie z intuicją, z analizy wymiarowej, dynamika układu będzie zależeć od stosunku dwóch wielkości. Weźmy dwie wielkości: \(a_1,\) \(a_2.\) Gdy wyrazimy \(a_2\) w charakterystycznej wielkości \(a_1,\) otrzymamy \(a_2/a_1\) – bezwymiarową wielkość, której poszukujemy!
Obliczmy coś.
Załóżmy, że celem przeprawy znajomego przez rwącą rzekę było spotkanie się z nami na umówioną oranżadę. Z tego powodu nie możemy się już doczekać jego przybycia, zatem z nudów zaczynamy wyliczać, kiedy wreszcie mu się uda dotrzeć.
Zacznijmy od naiwnego modelu, w którym zmęczenie powoduje działanie stałej, opóźniającej siły \(F,\) o wymiarze \(\left[F\right]=(\textrm{m} \cdot \textrm{kg})/(\textrm{s}^2).\) Możemy teraz wypisać równania ruchu: \[m\, \tilde{a} = -F,\] gdzie \(m\) to masa znajomego, \(\tilde{a}\) – jego przyspieszenie. Przypatrzmy się dokładniej powyższemu równaniu. Jest ono mało eleganckie – wielkości mają wymiary. Naprawmy to!
Pamiętamy z powyższych rozważań, że charakterystyczną miarą długości jest szerokość rzeki, zatem możemy od razu zastąpić \(\tilde{x}\) przez \(x L,\) ubezwymiarawiając położenie. Aby zobaczyć, jak taka zmiana wpływa na równanie, musimy przyjrzeć się definicjom przyspieszenia i prędkości: \[\tilde{a} = \frac{\Delta \tilde{v}}{\Delta t}, \ \ \ \tilde{v} = \frac{\Delta \tilde{x}}{\Delta t}.\] Podążając drogą ubezwymiarawiania, możemy zapisać: \(\Delta \tilde{x}=L \Delta x.\) W ten sposób \[\tilde{v} = \frac{L \Delta x}{\Delta t.}\] Skoro mamy już bezwymiarowe położenie, to nic nie powinno nam przeszkodzić w znalezieniu bezwymiarowego czasu. Zgodnie z wyrobioną przy położeniu procedurą szukamy charakterystycznej wielkości \(\alpha\) o wymiarze sekund. Wtedy czas wyrażamy w postaci \(t = \alpha \tau,\) gdzie \(\tau\) jest bezwymiarowe. W układzie mamy do dyspozycji wielkości: \(L,\) \(F,\) \(m\) i niewykorzystaną wcześniej prędkość początkową \(v_0.\) Dostajemy dwie kombinacje o wymiarze sekund: \(L/v_0\) i \(\sqrt{mL/F}\) (zachęcam Czytelnika do sprawdzania wymiarów, w każdym napisanym równaniu – praktyka czyni mistrza…).
W tym artykule wykorzystamy pierwsze skalowanie, czyli \(\alpha=L/v_0,\) drugie pozostawiam Czytelnikowi jako ćwiczenie na wykorzystanie wypracowanych tutaj metod. Fizycznie \(L/v_0\) to czas potrzebny na pokonanie \(L\) z prędkością \(v_0.\) Podstawiając skalowanie, dostajemy \(\Delta t = \alpha \Delta \tau=(L/v_0) \Delta \tau.\) Prędkość można wtedy zapisać jako: \[\tilde{v} = \frac{L \Delta x}{(L/v_0) \Delta \tau} = v_0 \frac{\Delta x}{\Delta \tau}=v_0\, v.\] Mierzymy prędkość w prędkości początkowej! \(v\) to bezwymiarowa prędkość. Dalej, pamiętając, że \(\Delta \tilde{v} = v_0 \Delta v,\) spójrzmy na przyspieszenie: \[\tilde{a} = \frac{\Delta \tilde{v}}{\Delta t} = \frac{v_0 \Delta v}{(L/v_0) \Delta \tau}=\frac{v_0^2}{L}\, a,\] gdzie \(a\) to bezwymiarowe przyspieszenie. Dostaliśmy naturalną miarę dla przyspieszenia, wykorzystajmy ją do równania ruchu: \[-F = m\, \tilde{a} = \frac{m v_0^2}{L}\, a.\] Przekształcając, dostajemy wreszcie: \[\tag{1} a = -\frac{F L}{m v_0^2}=- \frac{\xi}{2}. \label{eq:dimless}\] Otrzymaliśmy na końcu bezwymiarowe równanie – lewa i prawa strona mają wymiar 1. Przeanalizujmy wynik – nadajmy sens nowo oznaczonej, bezwymiarowej, wielkości \(\xi\) (do tego służy \(\frac{1}{2}\)). Ustawmy definicję tak, aby dało się zauważyć, co sobą reprezentuje: \[\tag{2} \xi = \left( F L\right)/ \left( \frac{m v_0^2}{2}\right). \label{eq:xi_def}\] Wprawny Czytelnik od razu rozpozna w mianowniku początkową energię kinetyczną znajomego, a w liczniku pracę wykonaną przez siłę oporu po pokonaniu całej rzeki. Po przekształceniach matematycznych dostaliśmy wielkość, która ma fizyczny sens!
I po co nam to było?
Namęczyliśmy się, i co z tego wynikło? Jeśli popatrzymy dogłębnie na równanie \(\eqref{eq:dimless}\) i poprzedzające rozumowanie, to otrzymamy kilka wniosków.
Po pierwsze, rozwiązaliśmy każdy ruch jednostajnie przyspieszony, konkretne krzywe pojawią się dla różnych wartości \(\xi,\) która w pewien sposób zależy od parametrów układu. W dodatku okazuje się, że równanie, zatem i rozwiązanie, wygląda identycznie dla dwóch różnych układów, ale o takiej samej wartości \(\xi.\) Po trzecie ruch jednostajnie przyspieszony zależy tylko od stosunku pracy wykonanej przez siłę na pewnym odcinku do energii kinetycznej na początku ruchu. W tak prostym przykładzie wydaje się to oczywistym wnioskiem, który mogliśmy uzyskać, nie ,,kombinując” z jednostkami, jednak w dużo bardziej skomplikowanych układach takie wnioskowanie może być wielce przydatne. Zatem przyjrzyjmy się tym bardziej skomplikowanym układom…
Liczba Reynoldsa.
Zaprzęgnijmy maszynerię z poprzedniego rozdziału do hydrodynamiki. W tekstach Sprawdź Wymiary! Jana Kalinowskiego, Zagadki hydrodynamiki i turbulencja Zbigniewa Peradzyńskiego (\(\Delta_{86}^{6}\)) oraz w większości problemów z dynamiki płynów pojawia się wielkość zwana liczbą Reynoldsa, \(Re.\) Można ją uzyskać na wiele sposobów, również korzystając z naszej metody.
Rys. 2. Pokazowa zmiana dynamiki układu wraz ze wzrostem \(Re.\) Sanatoshi Taneda, Karman vortex behind a circular cylinder, zdjęcia z An album of fluid motion, Milton van Dyke (1982). Zalecam lekturę Albumu, piękne ilustracje do całej gamy zjawisk w hydrodynamice
Weźmy równania Naviera–Stokesa (można o nich przeczytać np. w artykule Witolda Sadowskiego Równanie Naviera–Stokesa w \(\Delta_{12}^{14}\)). Zachęcam Czytelnika do sprawdzenia wymiarów: \[\rho \tilde{D_{t}} \tilde{u} = -\tilde{\nabla} \tilde{p} + \eta \tilde{\nabla}^2 \tilde{u,}\] gdzie: \(u\) – prędkość cieczy, \(D_t u\) – przyspieszenie cieczy (pochodna po czasie z prędkości na sterydach), \(\rho\) – gęstość cieczy, \(p\) – ciśnienie, \(\eta\) – lepkość dynamiczna (zob. Wyznaczamy współczynnik lepkości cieczy Stanisława Bednarka w \(\Delta_{08}^{8}\)). Wiele oznaczeń posiada symbol \(\tilde{\ },\) tak jak uprzednio, oznacza to, że wyrażenie ma wymiar. Niestety musimy tutaj użyć pochodnych cząstkowych, które operacyjnie są bardziej skomplikowane, ale ich ubezwymiarawianie przebiega identycznie – można je traktować jak zwykłą pochodną, a więc wyrażenie w postaci np. \([\tilde{\nabla} \tilde{u}] = [\Delta \tilde{u}/ \Delta \tilde{x}].\) Czyli z licznika wyjdzie skalowanie dla \(\tilde{u},\) a z mianownika skalowanie \(\tilde{x}.\)
Mierząc położenie w jednostkach pewnej charakterystycznej długości \(L,\) a prędkość w jednostkach charakterystycznej prędkości \(U,\) czas musimy naturalnie mierzyć w \(L/U,\) i podstawiając, dostajemy: \[\tilde{\nabla} = \frac{1}{L}\nabla \ \ \ \tilde{D_t} = \frac{U}{L} D_{\tau}.\] Wstawiając do równania Naviera–Stokesa i podstawiając \(\tilde{u} = u U,\) otrzymujemy: \[\rho \frac{U}{L} D_\tau \left( u U\right) = - \frac{1}{L}\nabla \tilde{p} + \eta \frac{1}{L^2} \nabla^2 ( u U).\] Przekształcając, dostajemy: \[D_\tau u = - \frac{1}{\rho U^2}\nabla \tilde{p} + \frac{\eta}{\rho U L} \nabla^2 u.\] Wprowadzając oznaczenie \(Re=\left(\rho U L\right)/\eta,\) dostaliśmy liczbę Reynoldsa!
Dodatkowo widzimy, że dobrą wielkością charakterystyczną dla ciśnienia jest \(\rho U^2.\) Podstawiając \(\tilde{p}= \rho U^2 p,\) kończymy z równaniem: \[D_\tau u = - \nabla p + \textcolor{var(--primary-color)}{ \frac{1}{Re} \nabla^2 u.}\] Przeanalizujmy uzyskane równanie. Lewa strona opisuje bezwładność cieczy. Pierwszy człon po prawej stronie jest gradientem ciśnienia. Drugi, kolorowy człon po prawej stronie odpowiada za siły lepkie. Patrząc z tej perspektywy na równanie, dowiadujemy się, że liczba \(Re\) określa, jak duży jest wpływ sił lepkości na dynamikę cieczy. Im mniejsza wartość \(Re,\) tym lepkość odgrywa ważniejszą rolę. Dla wystarczająco dużych wartości \(Re\) wpływ lepkości na dynamikę staje się zaniedbywalny.
Wielkość \(\rho U^2\) może słusznie kojarzyć się z zasadą Bernoulliego.
Podsumowując, liczbę Reynoldsa \(Re\) można zapisać jako stosunek: \[Re=\frac{\textrm{bezwładność cieczy}}{\textrm{siły lepkości}}.\]
Podsumowanie.
Każdy układ ma swoje liczby wymiarowe, a co za tym idzie – bezwymiarowe równanie opisujące je. Szukanie postaci bez jednostek pozwala na dogłębne zrozumienie jego dynamiki i zależności od istotnych zjawisk fizycznych. W ruchu znajomego po rzece: \[\xi=\frac{\textrm{praca sił}}{\textrm{energia kinetyczna}},\] w prostych układach hydrodynamicznych: \[Re=\frac{\textrm{bezwładność cieczy}}{\textrm{siły lepkości}},\] w artykule Nawijanie miodu z \(\Delta_{22}^{11}\): \[\kappa=\frac{\textrm{siły lepkości}}{\textrm{siły grawitacji}}.\] Przykładów jest wiele, szczególnie w dynamice płynów (polecam stronę Dimensionless numbers in fluid mechanics na Wikipedii), ale pojawiają się wszędzie. Zatem: Składajcie wymiary do 1!