Delta 12/2024

Zadania

Dominik Burek i Andrzej Majhofer

Zadanie M 1801

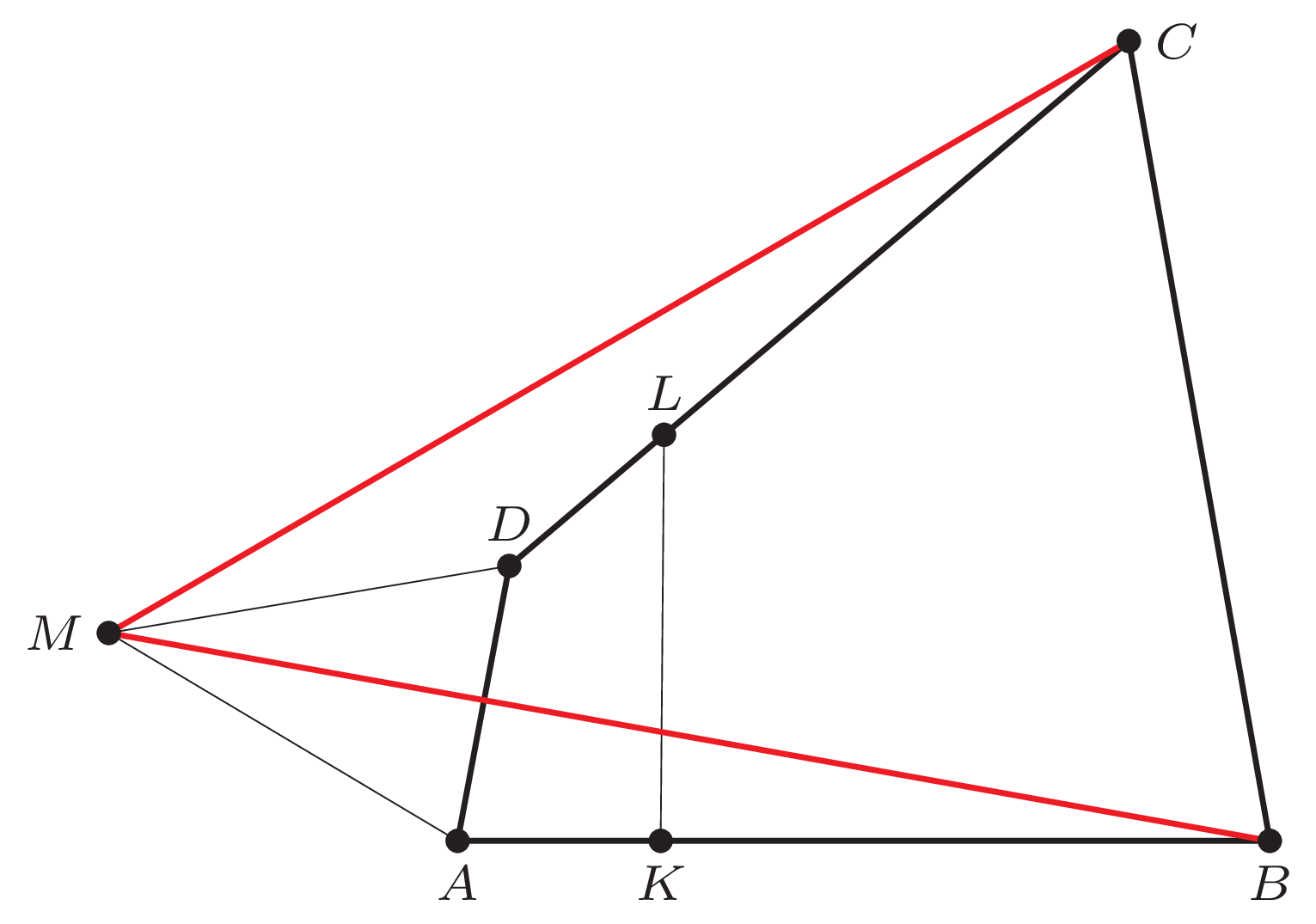
Dany jest czworokąt wypukły \(ABCD,\) w którym \({AB = BC = CD = 4.}\) Punkty \(K\) i \(L\) są wybrane, odpowiednio, na bokach \(AB\) i \(CD\) tak, że \({AK = DL = 1.}\) Trójkąt \(AMD\) jest zbudowany na boku \(AD\) na zewnątrz czworokąta, a ponadto \(AM = MD = 2.\) Załóżmy, że \(KL = 2.\) Udowodnić, że \({BM = CM}.\)

Rozwiązanie

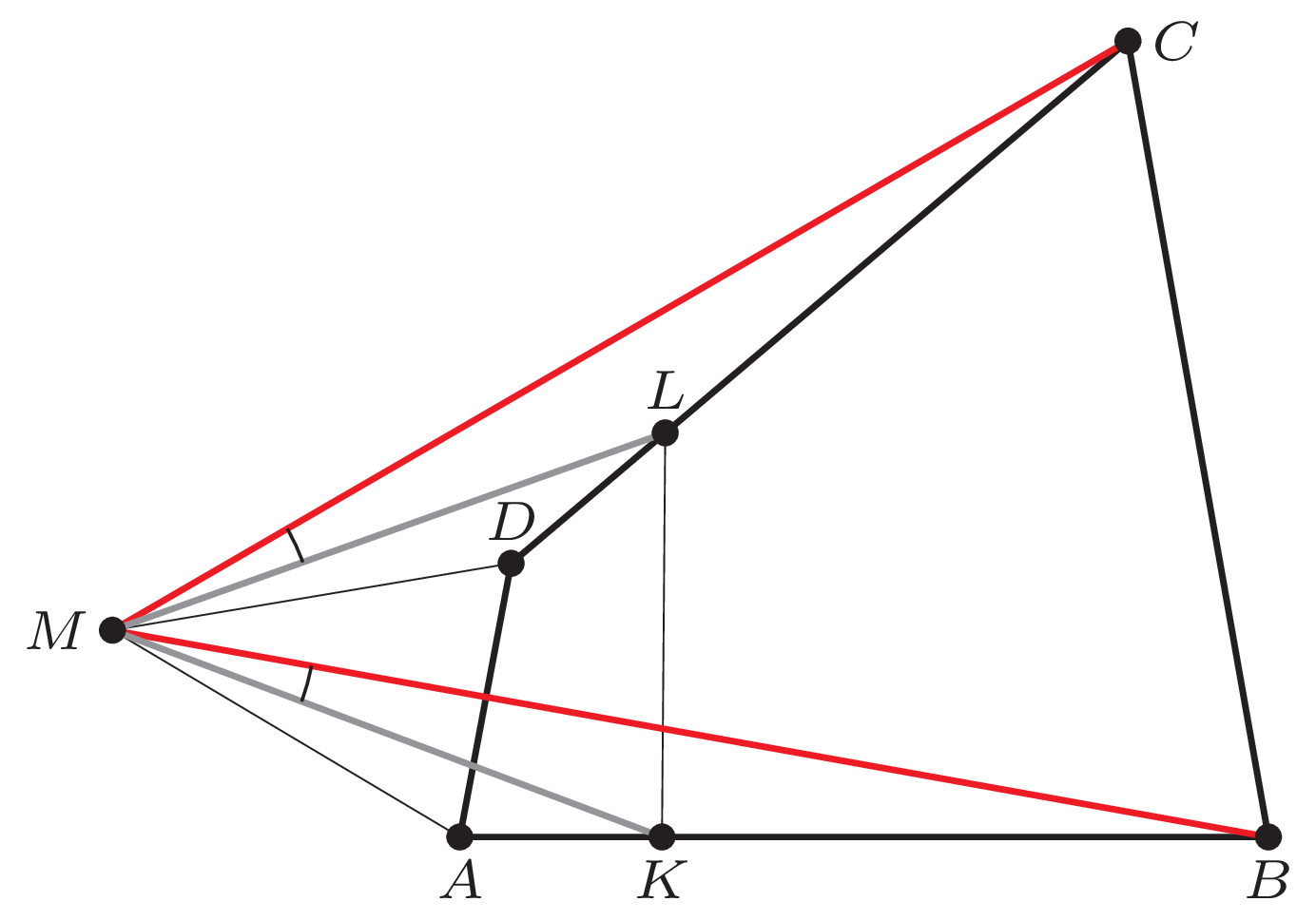
Zauważmy, że trójkąty \(MDL\) i \(CDM\) są podobne, a skala ich podobieństwa jest równa \(2\) (\(CD = 2MD,\) \(DM = 2DL,\) kąt przy wierzchołku \(D\) jest wspólny). W szczególności \(MC = 2 ML.\) Podobnie \(MB =2MK.\) Z założenia \({BC=2KL},\) więc trójkąt \(MKL\) jest podobny do trójkąta \(MBC.\) Zatem \(\measuredangle LMK = \measuredangle CMB,\) a stąd \(\measuredangle LMC = \measuredangle KMB.\) Oznacza to, że trójkąt \(LMC\) jest podobny do trójkąta \(KMB.\) Ale \(LC = KB,\) więc te trójkąty są przystające, skąd otrzymujemy, że \(BM = CM.\)

Zadanie M 1802

Komórki tabeli \(n \times n\) są wypełnione znakami ,,\(+\)” i ,,\(-\)”. Podczas ruchu można zmienić wszystkie znaki w dowolnym wierszu lub kolumnie na przeciwne. Wiadomo, że startując z początkowego układu, można w skończenie wielu ruchach zamienić wszystkie znaki w tabeli na plusy. Udowodnić, że można to osiągnąć, wykonując nie więcej niż \(n\) ruchów.

Rozwiązanie

Na początku zauważmy, że nie ma znaczenia, w jakiej kolejności zmieniane są znaki, ważne jest tylko to, w jakich wierszach i kolumnach (w skrócie liniach) następuje zmiana i ile razy. Jeśli w danym ruchu dwukrotnie zmienimy znaki, to nic się nie zmieni. Dlatego wystarczy zmienić znaki nie więcej niż raz w każdej linii.

Załóżmy, że udało nam się uzyskać wszystkie plusy, zmieniając znaki w \(k\) kolumnach i \(r\) wierszach. Jeżeli \(k+r > n,\) zaznaczmy na czerwono wszystkie linie, w których zmieniliśmy znaki. Znak zmienił się tylko w polach należących do dokładnie jednej czerwonej linii. Ale wtedy te same pola należą do dokładnie jednej niepomalowanej linii. Dlatego też rezultat byłby taki sam, gdybyśmy zmienili znaki w niepomalowanych liniach, a tych jest dokładnie \[(n - k) + (n -r)=2n-(k+r)<n.\]

Zadanie M 1803

Liczbę całkowitą dodatnią nazwiemy prawie kwadratem, jeśli można ją przedstawić jako iloczyn dwóch liczb, które różnią się nie więcej niż o \(1\%\) większej z nich. Udowodnić, że istnieje nieskończenie wiele czwórek kolejnych liczb naturalnych będących prawie kwadratami.

Rozwiązanie

Równanie \(2x^2-y^2=1\) ma rozwiązanie \((x,y)=(1,1).\) Ponadto zachodzi równość: \[2(3x+2y)^2-(4x+3y)^2=2x^2-y^2.\] Jeśli zatem \((x,y)\) rozwiązuje równanie \(2x^2-y^2=3,\) to \((3x+2y,4x+3y)\) również, stąd rozwiązań jest nieskończenie wiele. Weźmy takie rozwiązanie, dla którego \(y>1000\) i niech \(n=3xy.\) Wówczas \(2n^2 = 6x^2 * 3y^2 = (3y^2+3)\cdot (3y^2) = z^2+z-2,\) gdzie \(z=3y^2+1.\) Rozważmy \(4\) kolejne liczby i ich odpowiednie rozkłady: \[\begin{aligned} &4n^4-2=(z^2-2)(z^2+2z-1), \\ &4n^4-1=(2n^2-1)(2n^2+1), \\ &4n^4=2n^2\cdot 2n^2,\\ &4n^4+1=(2n^2+2n+1)(2n^2-2n+1). \end{aligned}\] Liczba \(4n^4\) jest oczywiście prawie kwadratem, natomiast z założenia \(y>1000\) dostaniemy, że każdy z ułamków \[\frac{z^2-2}{z^2+2z-1},\;\; \frac{2n^2-1}{2n^2+1},\;\; \frac{2n^2-2n+1}{2n^2+2n+1}\] jest równy co najmniej \(0{,}99\) – więc liczby \(4n^4-2,\) \(4n^4-1,\) \(4n^4+1\) są również prawie kwadratami.

Uwaga: Dobór liczb inspirowany jest tożsamością Sophie Germain. Równanie \(2x^2-y^2\) jest natomiast przykładem równania typu Pella i pod tym hasłem można znaleźć więcej informacji o sposobach znajdowania jego rozwiązań.

Krzywa rotacji typowej galaktyki spiralnej: (A) obliczona na podstawie obserwacji mas widocznych gwiazd, (B) obserwowana.

Zadanie F 1109

Krzywą rotacji galaktyki nazywany jest wykres zależności orbitalnych prędkości, \(v,\) widocznych gwiazd od ich odległości, \(r,\) od centrum galaktyki. Obserwowane zależności odbiegają od obliczonych na podstawie rozkładu mas widocznych gwiazd w galaktyce (rysunek). Dla wyjaśnienia tej rozbieżności przyjmuje się istnienie wewnątrz i wokół galaktyk niewidocznej tzw. ciemnej materii. Jak gęstość, \(\rho,\) ciemnej materii powinna zmieniać się z odległością, \(r,\) od centrum galaktyki w obszarze, w którym obserwowana prędkość ruchu orbitalnego gwiazd nie zależy od \(r\)? Przyjmij sferycznie symetryczny rozkład masy ciemnej materii.

Rozwiązanie

Prędkość, \(v,\) ciała obiegającego po orbicie o promieniu \(r\) środek sferycznie symetrycznego rozkładu masy zależy jedynie od \(M(r),\) tj. wielkości masy wewnątrz kuli o promieniu \(r,\) i wynosi (\(G\) oznacza stałą grawitacji): \[v(r) = \sqrt{\frac{GM(r)}{r}}.\] Znając \(v(r),\) możemy wyznaczyć \(M(r)\): \[M(r) = \frac{v^2r}{G}.\] W przypadku sferycznego rozkładu masy mamy: \[\frac{dM}{dr} = 4\pi r^2 \rho(r) = \frac{d}{dr}\left(\frac{v^2r}{G}\right).\] Po obliczeniu pochodnych otrzymujemy: \[\rho(r) = \frac{1}{4\pi r^2 G}\left(v^2 + 2vr\frac{dv}{dr}\right).\] W obszarze, gdzie \(v\) nie zmienia się ze zmianą \(r,\) mamy więc: \[\rho (r) = \frac{v^2}{4\pi r^2 G}.\]

Zadanie F 1110

Rowerzysta jedzie z prękością \(v\) po drodze pokrytej cienką warstwą błota. Nad kołami wyścigowego roweru nie ma błotników. Na jaką maksymalną wysokość mogą wznosić się cząstki błota oderwane od kół roweru. Koła mają promień \(R,\) przyspieszenie ziemskie równe jest \(g.\) Opór powietrza pomijamy.

Rozwiązanie

Cząstki (krople) błota odrywają się z prędkością styczną do koła i co do wartości równą prędkości roweru. Przeanalizujmy ruch kropli, która oderwała się z końca promienia tworzącego kąt \(\varphi\) z pionem (licząc od powierzchni drogi). W momencie oderwania kropla znajdowała się na wysokości \(h = R(1-\cos{\varphi})\) nad drogą i miała pionową składową prędkości równą \(v\sin{\varphi}.\) Najwyższy punkt toru jej ruchu (,,rzut ukośny”) znajdował się więc na wysokości: \[H = R(1-\cos{\varphi}) + \frac{v^2\sin^2{\varphi}}{2g}.\] Przyrównajmy pochodną \(H\) względem \(\varphi\) do zera: \[H' = R\sin{\varphi} + \frac{v^2 \sin{\varphi}\cos{\varphi}}{g} = 0.\] Gdy \(v^2 < gR,\) pochodna zeruje się jedynie dla \(\varphi = 0\) lub \(\varphi = \pi\) i maksymalna wysokość \(H = 2R\) (dla \(\varphi = \pi\)). Gdy \(v^2 > gR,\) zerowaniu pochodnej odpowiada także warunek: \[\cos{\varphi} = - \frac{gR}{v^2},\] co odpowiada \(\varphi > \pi/2\) i: \[H = R + \frac{gR^2}{2v^2} + \frac{v^2}{2g}.\]