Zbiór Cantora przed Cantorem

Zbiory, które przedstawimy w niniejszym artykule, są jednymi z najbardziej niezwykłych. Pojawiają się w wielu fragmentach współczesnej matematyki. Dzięki nim lepiej rozumiemy skomplikowaną strukturę zbioru liczb rzeczywistych oraz płaszczyzny euklidesowej. Nie można wykluczyć, że zbiory te wciąż skrywają własności, które czekają na swoich odkrywców.

W 1875 roku irlandzki matematyk Henry Smith w pracy [1] wykazał, że ograniczona funkcja rzeczywista będzie całkowalna w sensie Riemanna „[nawet, gdy jej punkty nieciągłości] będą istnieć w nieskończonej liczbie w skończonym przedziale bez wypełnienia jakiejkolwiek części tego przedziału”. Ten opis może nam się wydać odrobinę dziwny, ale proszę zauważyć, że powstał on w czasach, gdy nie istniała ani teoria mnogości, ani topologia, ani teoria miary, jakie znamy dzisiaj. Mimo to jest on zadziwiająco zgodny z dzisiejszym stanem wiedzy, który podsumowuje poniższy wynik.

Twierdzenie 1. Funkcja ograniczona w przedziale domkniętym $f:\mathrm{\Delta }\to \mathbb{R},$ $\mathrm{\Delta }\subset \mathbb{R},$ jest całkowalna w sensie Riemanna w tym przedziale wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma miarę Lebesgue’a równą zero.

Trafność sformułowania Smitha jeszcze lepiej widać, gdy spojrzymy na podane przez niego przykłady zbioru punktów, które „mogą istnieć w nieskończonej liczbie w skończonym przedziale bez wypełnienia jakiejkolwiek części tego przedziału”.

Przykład 1 (Smith, 1875). Niech $m$ będzie dowolną liczbą całkowitą większą od 2. Podzielmy przedział $[0,1]$ na $m$ równych przedziałów i usuńmy ostatni segment („segment” to taki przedział, że to, co zostaje po jego usunięciu, jest zbiorem domkniętym). Każdy z pozostałych $m-1$ przedziałów podzielmy na $m$ równych przedziałów i usuńmy ostatni segment z każdego z nich (rys. 1).

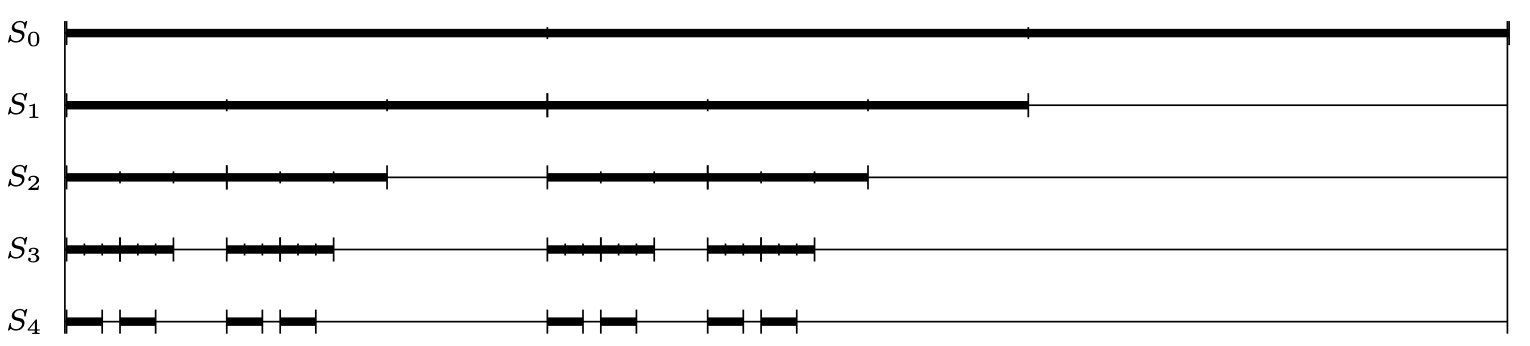
Rys. 1. Pierwsze etapy konstrukcji Smitha dla $m=3$

Jeżeli ta operacja będzie kontynuowana w nieskończoność, to otrzymamy domknięty zbiór $\mathcal{S}$ o nieskończonej liczbie punktów, który nie wypełnia jakiejkolwiek części przedziału $[0,1].$ Łączna długość przedziałów, jakie pozostają po $k$-tym kroku konstrukcji, jest równa $(\frac{m-1}{m}{)}^k$ i dąży do 0, gdy $k\to \mathrm{\infty }.$ Jednocześnie po $k$ krokach konstrukcji długość usuniętych przedziałów jest równa $1-(\frac{m-1}{m}{)}^k$ i dąży do 1, gdy $k\to \mathrm{\infty }.$ Zbiór $\mathcal{S}$ nazywamy zbiorem Smitha.

Opisana konstrukcja Smitha to jeden z najwcześniejszych opublikowanych przykładów zbioru fraktalnego (samopodobnego) utworzonego rekurencyjnie!

Przejdźmy do omówienia tytułowego zbioru Cantora. W latach 1879–1884 matematyk niemiecki Georg Cantor badał topologiczne własności podzbiorów zbioru liczb rzeczywistych. W pracy [2], bez wskazania motywacji, podał przykład zbioru doskonałego i nigdziegęstego (to dla purystów, bo dalszy tekst nie wymaga znajomości tych pojęć).

Przykład 2 (Cantor, 1883). Zbiór liczb postaci $$\mathcal{C}=\{x\in \mathbb{R}:x=\sum _{i=1}^{\mathrm{\infty }}\frac{c_i}{3^i},\text{gdzie}{c}_i\in \{0,2\}\},$$ nazywamy zbiorem Cantora.

Zbiór Cantora tworzą zatem te liczby z przedziału $[0,1],$ które można zapisać w systemie trójkowym w postaci nieskończonego rozwinięcia przy użyciu tylko cyfr 0 lub 2. Należy przy tym pamiętać, że np. $\frac{1}{3}\in \mathcal{C},$ bo $\frac{1}{3}=(\mathrm{0,022}2\dots {)}_3,$ a nie tylko $\frac{1}{3}=(0,1{)}_3.$

Zauważmy teraz, że w rozwinięciu $x=(0,c_1{c}_2{c}_3\dots {)}_3,$

Ponieważ prawdziwe są również implikacje odwrotne, więc zbiór Cantora możemy opisać geometrycznie: podzielmy przedział $[0,1]$ na trzy równe przedziały i usuńmy otwarty przedział środkowy. Każdy z pozostałych przedziałów podzielmy na trzy równe przedziały i z każdego takiego podziału usuńmy otwarty przedział środkowy. Jeżeli ta operacja będzie kontynuowana w nieskończoność, to otrzymamy w przedziale $[0,1]$ domknięty zbiór $\mathcal{C}$ (rys. 2).

Rys. 2. Pierwsze etapy geometrycznej konstrukcji zbioru Cantora

Podobnie jak w przykładzie 1, „długość” (w dzisiejszym języku: miara) zbioru Cantora jest równa 0.

Porównując geometryczne konstrukcje zbioru Smitha (dla $m=3$) i zbioru Cantora, stwierdzamy, że $$\mathcal{S}=\{x\in \mathbb{R}:x=\sum _{i=1}^{\mathrm{\infty }}\frac{s_i}{3^i},\text{gdzie}{s}_i\in \{0,1\}\}\text{i}2\cdot \mathcal{S}=\mathcal{C}.$$ Przy próbie rysowania przybliżeń zbioru Cantora widzimy jedynie wymierne końce wybranych przedziałów, których jest przeliczalnie wiele. Czy w zbiorze Cantora są inne liczby? Pokażemy (dwoma sposobami), że $\frac{1}{4}\in \mathcal{C},$ choć nie jest końcem jakiegokolwiek przedziału z konstrukcji zbioru Cantora.

Sposób 1. Punkty $x_1=\frac{1}{3},$ $x_2=\frac{1}{3}-\frac{1}{9},$ $x_3=\frac{1}{3}-\frac{1}{9}+\frac{1}{27}$ itd. są końcami przedziałów w konstrukcji zbioru Cantora, więc należą do zbioru $\mathcal{C}.$ Jednocześnie $(\frac{1}{3})-(\frac{1}{3}{)}^2+(\frac{1}{3}{)}^3-\cdots =\frac{1}{4},$ więc $\frac{1}{4}\in \mathcal{C},$ bo zbiór $\mathcal{C}$ jest domknięty.

Sposób 2. Z definicji zbioru Cantora $x=(\mathrm{0,020}202\dots {)}_3\in \mathcal{C}.$ Ponieważ $$x=\frac{2}{3^2}+\frac{2}{3^4}+\frac{2}{3^6}+\cdots =\frac{1}{3^2}(2+[\frac{2}{3^2}+\frac{2}{3^4}+\dots ])=\frac{1}{9}(2+x),$$ więc $x=\frac{1}{4}\in \mathcal{C}.$

Twórca teorii mnogości wiedział, że zbiór $\mathcal{M}$ wszystkich nieskończonych ciągów utworzonych z 0 lub 1 jest nieprzeliczalny, to znaczy nie da się utworzyć ciągu złożonego z wszystkich jego elementów.

Uzasadnienie jest łatwe. Załóżmy, że wszystkie elementy zbioru $\mathcal{M}$ (będące ciągami) zostały ponumerowane liczbami naturalnymi (zostały ustawione w ciąg): $M_1=\{m_i^1{\}}_{i=1}^{\mathrm{\infty }},$ $M_2=\{m_i^2{\}}_{i=1}^{\mathrm{\infty }},$ $\dots$ Tworzymy nowy ciąg $T=\{t_i{\}}_{i=1}^{\mathrm{\infty }},$ który na $i$-tym miejscu różni się od ciągu $M_i,$ przyjmując, że jeśli $m_i^i=0,$ to $t_i=1,$ a jeśli $m_i^i=1,$ to $t_i=0.$ Wtedy ciąg $T$ $\text{należy do}$ $\mathcal{M}$ (bo zbudowany jest z 0 lub 1) i $T\ne M_i$ dla każdego $i=1,2,\dots$ Jest to sprzeczne z założeniem, że wszystkie elementy zbioru $\mathcal{M}$ zostały ponumerowane liczbami naturalnymi, więc $\mathcal{M}$ jest zbiorem nieprzeliczalnym.

Z poczynionych obserwacji wynikają następujące stwierdzenia.

Twierdzenie 2:

1. Zbiór Smitha ma tyle samo elementów co zbiór Cantora (równoliczność ustala funkcja mnożenia przez 2, czyli$$\mathcal{S}\ni (0,s_1{s}_2{s}_3\dots {)}_3⟼(0,c_1{c}_2{c}_3\dots {)}_3\in \mathcal{C},$$ gdzie $s_i\in \{0,1\}$ i $c_i=2s_i$ dla każdego $i=1,2,\dots$);

2. Zbiór Smitha $($zbiór Cantora$)$ jest nieprzeliczalny.

Stwierdzenie (2) możemy wzmocnić, wykazując, że przekształcenie $$f((0,c_1{c}_2{c}_3\dots {)}_3)=\frac{1}{2}\sum _{i=1}^{\mathrm{\infty }}\frac{c_i}{2^i},\text{gdzie}{c}_i\in \{0,2\},$$ odwzorowuje w sposób ciągły zbiór Cantora $\mathcal{C}$ na przedział $[0,1].$ Wynika stąd, że zbiór $\mathcal{C}$ ma nie mniej elementów niż jego obraz $f(\mathcal{C})=[0,1].$ Ponieważ $\mathcal{C}\subset [0,1],$ więc zbiór Cantora ma tyle samo elementów co przedział $[0,1].$

Zatem większości liczb ze zbioru Cantora (zbioru Smitha) nie widzimy (!), choć jest ich tak dużo jak w całym przedziale $[0,1],$ i na dodatek wszystkie one mieszczą się na „odcinku” zerowej długości! Doprawdy niewiarygodne, jak matematyka potrafi zaskoczyć naszą intuicję i poruszyć wyobraźnię.

Jakby tego było mało, okazuje się, że ten „mały” zbiór może tworzyć zaskakująco duże zbiory, na przykład $$\mathcal{C}+\mathcal{C}=\{x+y:x,y\in \mathcal{C}\}=[0,2].$$ Uzasadnienie jest następujące. Ponieważ $\mathcal{C}\subset [0,1],$ więc oczywiście $\mathcal{C}+\mathcal{C}\subset [0,2].$ Aby wykazać zawieranie przeciwne, ustalmy liczbę $t\in [0,2].$ Musimy wskazać dwie liczby $b,d\in \mathcal{C}$ takie, że $b+d=t.$ Zauważmy, że jeśli $C_1=[0,\frac{1}{3}]\cup [\frac{2}{3},1],$ to $\{x+y:x,y\in C_1\}=[0,2].$ Powody wyjaśnia rysunek 3 (to jedna z możliwych realizacji).

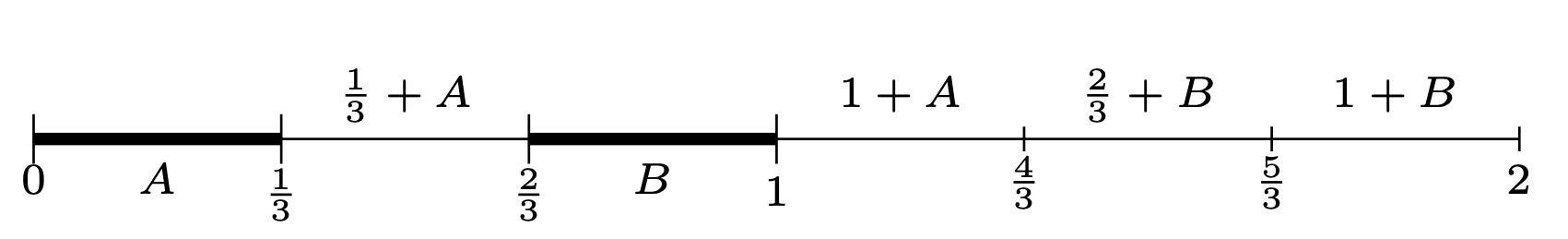
Rys. 3. Pierwsze etapy geometrycznej konstrukcji zbioru Cantora

Zatem istnieją liczby $b_1,d_1\in C_1$ takie, że $b_1+d_1=t.$ Analogicznie, jeśli $C_2=[0,\frac{1}{9}]\cup [\frac{2}{9},\frac{1}{3}]\cup [\frac{2}{3},\frac{7}{9}]\cup [\frac{8}{9},1],$ to $\{x+y:x,y\in C_2\}=[0,2].$ Istnieją więc liczby $b_2,d_2\in C_2$ takie, że $b_2+d_2=t.$ Kontynuując to postępowanie, możemy dla każdego $i$ znaleźć liczby $b_i,d_i\in C_i$ takie, że $b_i+d_i=t.$ Oczywiście ciągi $\{b_i{\}}_{i=1}^{\mathrm{\infty }},\{d_i{\}}_{i=1}^{\mathrm{\infty }}\text{ zawierają się w }\mathcal{C},$ więc korzystając ze zwartości zbioru $\mathcal{C},$ możemy uzasadnić istnienie podciągów $\{b_{i_k}{\}}_{k=1}^{\mathrm{\infty }},$ $\{d_{i_k}{\}}_{k=1}^{\mathrm{\infty }},$ które są zbieżne do liczb $b,d\in \mathcal{C},$ odpowiednio. Ponieważ przechodzenie do granicy zachowuje operację dodawania, więc przechodząc z $k\to \mathrm{\infty }$ w równaniu $b_{i_k}+d_{i_k}=t,$ otrzymujemy $b+d=t.$ Zatem $[0,2]\subset \mathcal{C}+\mathcal{C},$ co kończy uzasadnienie. Podobnie moglibyśmy również pokazać, że $\mathcal{C}-\mathcal{C}=[-1,1].$

Obserwacje te mogą stanowić naturalny punkt wyjścia do rozważań nad miarą, kategorią i wymiarem zbiorów, i de facto stały się impulsem do rozwoju tych teorii na przełomie XIX i XX wieku. Problematyka ta jest jeszcze lepiej widoczna na tle uwagi Smitha z pracy [1]: „rozważając dla uproszczenia przypadek dwóch wymiarów, zauważmy, że [skończony przedział (czyli prostokąt) całkowania] może nie tylko zawierać punkty nieciągłości o skończonej lub nieskończonej liczbie, ale może być także przecięty krzywymi nieciągłości (…), nawet gdy całkowita długość krzywych nieciągłości jest nieskończona, [bez wypełnienia jakiejkolwiek części przedziału całkowania]”.

Możemy spekulować, że Smith, zanim wyraził tę myśl, wyobraził sobie dwuwymiarową wersję konstrukcji z przykładu 1 (dla $m=3$). Kwadrat jednostkowy $[0,1{]}^2$ dzielimy na 9 przystających kwadratów i usuwamy kwadrat (segment) w prawym dolnym rogu. Każdy z 8 pozostałych kwadratów dzielimy na 9 przystających kwadratów i w każdym z nich usuwamy kwadrat (segment) w prawym dolnym rogu. Dla pozostałych 64 kwadratów operację powtarzamy. Kontynuując tę operację w nieskończoność, otrzymamy zbiór, który „nie wypełnia jakiejkolwiek części kwadratu $[0,1{]}^2$”. Pole pozostałe w $k$-tym kroku konstrukcji jest równe $(\frac{8}{9}{)}^k$ i dąży do 0, gdy $k\to \mathrm{\infty }$ (rys. 4).

Rys. 4. Pierwsza, druga i czwarta iteracja konstrukcji płaskiego zbioru Smitha dla $(m=3)$

Dodatkowo prawa dolna granica powstałego zbioru jest wersją krzywej płatka śniegu (o nieskończonej długości) opublikowanej przez Helge von Kocha w 1904 roku.

Patrząc na opisane w artykule konstrukcje, nabieramy szacunku do pozornie prostych pytań: co to jest linia? co to jest powierzchnia? Odpowiedź na każde z nich… wcale nie jest łatwa!

I na koniec ciekawostka. Jeśli wyżej opisaną płaską konstrukcję Smitha wykonamy dla $m=2,$ to otrzymamy$\dots$ wersję trójkąta Sierpińskiego (!), który został opublikowany w 1915 roku (rys. 5).

Rys. 5. Druga, czwarta i szósta iteracja konstrukcji płaskiego zbioru Smitha dla $(m=2)$

Ale w 1875 roku Wacława Sierpińskiego nie było jeszcze na świecie! Ach, co by to było, gdyby Smith miał komputer$\dots$

Literatura

1. H.J.S. Smith, „On the integration of discontinuous functions”, Proc. London Math. Soc. (1) 6 (1875), 140–153.

2. G. Cantor, „Uber unendliche lineare Punktmannichfaltigkeiten”, V, Math. Ann. 21 (1883), 545–591.