Tablice trygonometryczne, logarytmiczne, astronomiczne czy tablice liczb losowych w czasach przedkomputerowych pełniły rolę swoistej konserwy, w której zakumulowano wysiłek wielu rachmistrzów. Kopciuszkiem w tym gronie była tabliczka mnożenia. Okazało się, że w XX wieku sławne tablice przestały być potrzebne, a tabliczkę mnożenia czekała całkiem nowa i nieoczekiwana rola.
Inspiracją do napisania niniejszego artykułu była fascynująca historia tablic matematycznych przedstawiona w [1]. Zainteresowanym tablicami liczb losowych polecam również lekturę [2].
Tabliczka mnożenia.
Kwadratowa tabliczka mnożenia – taka, jaką znamy,
| 1 | 2 | \(\ldots\) | 9 | 1 |
| 2 | 4 | \(\ldots\) | 18 | 2 |
| \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) |
| 9 | 18 | \(\ldots\) | 81 | 9 |
| 1 | 2 | \(\ldots\) | 9 |
zawiera wyniki mnożenia przez siebie liczb od 1 do 9. Dzięki jej zapamiętaniu (to ta konserwa rachunkowa, która pozostaje w głowie na całe życie) można opanować mnożenie pisemne dwóch dowolnych liczb. I nie wydaje się, aby do czegoś więcej można było takiej tabliczki użyć.
Będziemy interesować się tablicami \(T=\left[t_{ij}\right]\) o \(I\) wierszach i \(J\) kolumnach, składającymi się z liczb rzeczywistych dodatnich. Powiemy, że tablica \(T\) jest tabliczką mnożenia \(TM(\mathbf{\boldsymbol{w}}\boldsymbol{,k})\) o czynnikach: wierszowym \(\mathbf{w}=\left[w_{1},w_{2},\ldots,w_{I}\right]\) i kolumnowym \(\mathbf{k}=\left[k_{1},k_{2},\ldots,k_{J}\right],\) gdy \[t_{ij}=w_{i}k_{j}\;\textrm{dla }\:i=1,2,\ldots,I,\:j=1,2,\ldots,J.\] Nietrudno zauważyć, że tablica
\(T_{1}=\)
| 14 | 28 | 56 | 112 | 210 | 700 | 1400 |
| 13 | 26 | 52 | 104 | 195 | 650 | 1300 |
jest tabliczką mnożenia:
| 14 | 28 | 56 | 112 | 210 | 700 | 1400 | 0,14 |
| 13 | 26 | 52 | 104 | 195 | 650 | 1300 | 0,13 |
| 100 | 200 | 400 | 800 | 1500 | 5000 | 10 000 |
Liczby w powyższej tabliczce zostały wybrane nieprzypadkowo. Tabliczka mnożenia \(T_{1}\) okazuje się przyzwoitym przybliżeniem tabeli aktualnych rekordów świata kobiet i mężczyzn w biegach (wyrażonych w sekundach):
\(T_{0}=\)
| 10,49 | 21,34 | 47,60 | 113,28 | 230,07 | 846,62 | 1741,03 | kobiety |
| 9,58 | 19,19 | 43,03 | 100,91 | 206,00 | 755,36 | 1571,00 | mężczyźni |
| 100 m | 200 m | 400 m | 800 m | 1500 m | 5000 m | 10 000 m |
Związek tablic \(T\) i \(TM(\mathbf{\boldsymbol{w}}\boldsymbol{,k})\) wygodnie jest przedstawić w postaci reprezentacji resztowej \(T\) względem \(TM(\mathbf{\boldsymbol{w}}\boldsymbol{,k})\):
| R | w |
| k |
Elementy \(r_{ij}\) tablicy resztowej \(R=R(\textbf{w},\textbf{k})\) wyznaczone są z warunku \({t_{ij}=r_{ij}w_ik_j.}\)
Reprezentacja resztowa \(T_0\) względem \(T_1\) ma, z dokładnością do 0,001, postać
| 0,749 | 0,762 | 0,850 | 1,011 | 1,096 | 1,209 | 1,244 | 0,14 |
| 0,737 | 0,738 | 0,828 | 0,970 | 1,056 | 1,162 | 1,208 | 0,13 |
| 100 | 200 | 400 | 800 | 1500 | 5000 | 10000 |
Rzecz jasna, nie każda tabela jest tabliczką mnożenia. Z definicji wynika, że dowolne dwa jej wiersze muszą być proporcjonalne, czyli stosunek odpowiadających wyrazów tych wierszy musi być stały (i równy stosunkowi odpowiednich wyrazów czynnika kolumnowego). W takim wypadku mówimy o jednorodności wierszy. Gdyby w tabeli rekordów w biegach \(T_{0}\) występowała jednorodność wierszy, to wyniki mężczyzn byłyby proporcjonalne do wyników kobiet. W rzeczywistości wiersze są prawie jednorodne. Stosunek czasu mężczyzn do czasu kobiet jest niemal równy na wszystkich dystansach:
| 0,913 | 0,899 | 0,904 | 0,891 | 0,895 | 0,892 | 0,902 |
| 100 m | 200 m | 400 m | 800 m | 1500 m | 5000 m | 10 000 m |
Tabeli rekordów nie możemy zatem przedstawić jako tabliczki mnożenia. Jednorodność wierszy jest jednocześnie warunkiem dostatecznym – jeśli występuje, jesteśmy w stanie dobrać czynniki wierszowy i kolumnowy, by uzyskać daną tablicę jako tabliczkę mnożenia. W analogiczny sposób możemy zdefiniować jednorodność kolumn, która również jest warunkiem koniecznym i dostatecznym do tego, by dana tablica była tabliczką mnożenia.
Przedstawimy teraz nieco bardziej skomplikowane kryterium, któremu jednak będziemy mogli nadać pewien statystyczny charakter. Oznaczmy: \[\begin{aligned} t_{i1}+t_{i2}+\ldots+t_{iJ} & =t_{i+}, \\ t_{1j}+t_{2j}+\ldots+t_{Ij} & =t_{+j}, \\ \sum_{i=1}^{I}\sum_{j=1}^{J}t_{ij} & =t_{++}. \end{aligned}\] Można pokazać, że tabela \(T\) jest tabliczką mnożenia wtedy i tylko wtedy, gdy \[\tag{1}\label{eq:multy} t_{ij}=\frac{t_{i+}t_{+j}}{t_{++}} \ \ \ \textnormal{dla każdego}\:i,j.\] Warunek ten nazwiemy kryterium multiplikatywnym. Prześledźmy je na następującym przykładzie. Wylosowano 600 studentów Uniwersytetu Delaware i zanotowano ich kolor oczu i włosów.
| WŁOSY | OCZY | |||
| brązowe | niebieskie | szare | zielone | |
| czarne | 68 | 20 | 15 | 5 |
| szatynowe | 119 | 84 | 54 | 29 |
| rude | 26 | 17 | 14 | 14 |
| blond | 7 | 94 | 10 | 16 |
Gdyby to była tabliczka mnożenia, to musiałaby zachodzić równość \(\eqref{eq:multy}\), równoważna równości \[\tag{2} \frac{t_{ij}}{t_{++}}=\frac{t_{i+}}{t_{++}}\frac{t_{+j}}{t_{++}} \ \ \ \textnormal{dla każdego}\:i,j.% \label{eq:2}\] Zwróćmy uwagę, że \(\frac{t_{i+}}{t_{++}}\) jest oszacowaniem prawdopodobieństwa wystąpienia \(i\)-tego koloru włosów, \(\frac{t_{+j}}{t_{++}}\) oszacowaniem prawdopodobieństwa wystąpienia \(j\)-tego koloru oczu, zaś \(\frac{t_{ij}}{t_{++}}\) – prawdopodobieństwa jednoczesnego wystąpienia kolorów \(i\) oraz \(j.\)
Warunek \(\eqref{eq:2}\) oznacza, że prawdopodobieństwo jednoczesnego wystąpienia koloru włosów \(i\) oraz koloru oczu \(j\) jest iloczynem ich prawdopodobieństw. W rachunku prawdopodobieństwa taki warunek oznaczałby niezależność koloru oczu i włosów. W tym przypadku warunek ten nie jest spełniony – nie mamy zatem do czynienia z tabliczką mnożenia.
W naszej tabeli \(t_{11}=68,\) \(t_{1+}=108,\) \(t_{+1}=220,\) \(t_{++}=592\) oraz \[\frac{68}{592}\neq\frac{108}{592}\frac{220}{592}.\]
Jak daleko od tabliczki mnożenia?
Tabela rekordów w biegach i tabela koloru oczu i włosów nie są tabliczkami mnożenia. Wszystkie symptomy wskazują jednak, że tabela rekordów jest bardzo podobna do jakiejś tabliczki mnożenia – tabela kolorów nie wydaje się podobna do żadnej. Jak to zmierzyć?
Zróżnicowanie \(z(T,U)\) tabel \(T\) i \(U\) o tych samych rozmiarach \(I\times J\) zdefiniujemy jako średnie zróżnicowanie \(z(t_{ij},u_{ij})\) ich elementów. Naturalną średnią w tym przypadku jest średnia geometryczna. Wynika to z faktu, że mnożenie jest działaniem naturalnym dla tabliczek mnożenia, a średnia geometryczna \(g\) liczb \(x_1,\ldots,x_n\) spełnia \(x_{1}\cdot x_{2}\cdot \ldots\cdot x_{n}=g^n.\)
Liczba \(y\) jest średnią (średnią De Morgana) zbioru liczb \(\left\{ x_{1},x_{2},\ldots,x_{n}\right\}\) względem łącznego i przemiennego działania \(\circledast,\) jeśli \(x_{1}\circledast x_{2}\circledast\ldots\circledast x_{n}=y\circledast y\circledast\ldots\circledast y\) (\(n\) razy). Średnia geometryczna jest zatem średnią względem mnożenia.
Samo zaś zróżnicowanie \(z(a,b)\) dwóch liczb dodatnich \(a\) i \(b\) powinno spełniać warunki:
Symetria: \(z(a,b)=z(b,a)\);
Niezależność od wyboru jednostek: dla każdego \(s>0,z(a,b)=z(sa,sb)\);
Monotoniczność: funkcja \(f \colon [1,\infty) \to \mathbb{R}\) określona wzorem \(\smash{f(a)\stackrel{df}{=}z(a,1)}\) jest rosnąca.
Funkcję \(f\) z warunku 3 będziemy nazywać funkcją skalującą. Łatwo jest wykazać, że zróżnicowanie \(z(a,b)\) wyraża się wzorem \[z(a,b) = f \left( \max{\left( \frac{a}{b},\frac{b}{a} \right)}\right).\] Oczywistym, najprostszym wyborem funkcji skalującej \(f\) jest \(f(a)=a.\) Wtedy \[z(a,b) = \max{ \left(\frac{a}{b},\frac{b}{a}\right)}.\] Liczba \(z(a,b)\) jest wówczas wielkością korygującą \(a\) tak, aby przez pomnożenie lub podzielenie przez nią otrzymać \(b.\) Właśnie takie określenie zróżnicowania \(z(a,b)\) przyjmujemy w dalszej części tekstu.
Dla logarytmicznej funkcji skalującej \[\begin{split} z(a,b) & =\log\left(\max\left(\frac{a}{b},\frac{b}{a}\right)\right) \\&=\left|\log\left(a\right)-\log\left(b\right)\right|. \end{split}\]
Zróżnicowanie \(z \left(T,TM(\boldsymbol{w},\boldsymbol{k})\right) =\left( {\prod_i \prod_j z\left(t_{ij},w_i k_j\right)}\right)^{1/IJ}\) można wyrazić poprzez tabelę resztową \[z\left(T,TM(\boldsymbol{w},\boldsymbol{k})\right) = z\left(R(\boldsymbol{w},\boldsymbol{k}), \mathcal{J} \right) = \left({\prod_i~\prod_j z\left(r_{ij},1 \right)} \right)^{1/IJ},\] gdzie \(\mathcal{J}\) jest tablicą jedynek rozmiaru \(I\times J,\) a \(z\left( r_{ij},1\right)=\max\left( r_{ij}, r_{ij}^{-1}\right).\) Zróżnicowanie tablic \(T_0\) i \(T_1\) z pierwszego przykładu jest równe \[z(T_{0},T_{1})=\sqrt[14]{{0{,}749}^{-1}\cdot {0{,}762}^{-1}\cdot \ldots\cdot 1{,}208}\simeq1{,}19,\] co oznacza, że średnia korekta elementów \(T_1,\) aby otrzymać \(T_0,\) wynosi 19%.
Reprezentacja optymalna.
Tabliczkę mnożenia najbardziej podobną do danej tabeli \(T\) nazywamy optymalną reprezentacją \(T.\)
Innymi słowy, reprezentacja optymalna tabeli \(T\) jest tabliczką mnożenia \(TM(\boldsymbol{w_{0}},\boldsymbol{k_{0}})\) spełniającą warunek \[z\left(T,TM(\boldsymbol{w_{0}},\boldsymbol{k_{0}})\right)\leq z\left(T,TM(\boldsymbol{w},\boldsymbol{k})\right),\] równoważnie \[z\left(R(\boldsymbol{w_{0}},\boldsymbol{k_{0}}),\mathcal{J}\right)\leq z\left(R(\boldsymbol{w},\boldsymbol{k}),\mathcal{J}\right),\] dla dowolnych \(\boldsymbol{w}\) i \(\boldsymbol{k}.\) Liczbę \(\operatorname{Ind}\left(T\right)\stackrel{df}{=}z\left(T,TM(\boldsymbol{w_{0}},\boldsymbol{k_{0}})\right)\) nazywamy indeksem tabeli \(T.\)
Tablica resztowa optymalnej reprezentacji \(T\) jest najbardziej podobna do tablicy jedynek \(\mathcal{J}\) spośród wszystkich reprezentacji \(T.\)
Optymalna reprezentacja resztowa tabeli \(T_{0}\) rekordów w biegach to
| 0,992 | 1,000 | 0,997 | 1,005 | 1,002 | 1,004 | 0,998 | 21,340 |
| 1,008 | 1,000 | 1,003 | 0,995 | 0,998 | 0,996 | 1,002 | 19,190 |
| 0,495 | 1,000 | 2,236 | 5,283 | 10,758 | 39,517 | 81,725 |
Indeks tabeli \(T_0\) jest równy 1,0033. Rekordy kobiet i mężczyzn na wszystkich dystansach są praktycznie takie same z dokładnością do efektu płci” \(21{,}34/19{,}19 \approx 1{,}1120.\) Efekt ten oznacza, że kobiety mają dłuższy średnio o 11% czas biegu na każdym dystansie.
Powstaje naturalne pytanie, jak rozpoznać optymalną reprezentację danej tabeli? Do sformułowania warunku koniecznego potrzebne jest pojęcie mediany.
Mediana ciągu \(x=\left(x_1,x_2,\ldots,x_n \right)\) jest liczbą \(m\) o tej własności, że co najmniej połowa elementów \(x\) spełnia warunek \(x_i \leq m\) i co najmniej połowa – warunek \(x_i \geq m.\) Gdy liczba \(n\) jest nieparzysta, to mediana jest wyznaczona jednoznacznie, gdy parzysta – możliwe wartości mediany tworzą przedział domknięty.
Można pokazać, że dla dowolnego ciągu liczb dodatnich \(x=\left(x_1,x_2,\ldots,x_n \right)\) średnia geometryczna \(\sqrt[n]{\prod_{i=1}^{n}z\left(x_{i},m\right)}\) osiąga wartość minimalną tylko wtedy, gdy \(m\) jest medianą zbioru. Obserwacja ta jest podstawą poniższego twierdzenia.
Twierdzenie. Warunkiem koniecznym na to, by tabliczka mnożenia \(TM(\boldsymbol{w_{0}},\boldsymbol{k_{0}})\) była optymalną reprezentacją \(T,\) jest to, aby liczba 1 należała do mediany każdego wiersza i każdej kolumny tabeli resztowej \(R(\boldsymbol{w_{0}},\boldsymbol{k_{0}}).\)
Metodę przekształcenia tabeli danych tak, aby spełniła ten warunek, zwaną wygładzaniem medianowym (ang. median polish), wykorzystał w analizie statystycznej John Tukey (1915–2000). Analiza ta prowadzona jest w języku addytywnym, a nie multiplikatywnym, jak w naszym przypadku.
Warunek ten nie jest dostateczny. Tabela
\(T=\)
| 5 | 1 | 1 |
| 15 | 4 | 3 |
| 10 | 2 | 4 |
ma dwie reprezentacje spełniające warunek konieczny:
\(T=\)
| 4/3 | 1 | 1 | 1/4 |
| 1 | 1 | 3/4 | 1 |
| 1 | 3/4 | 3/2 | 2/3 |
| 15 | 4 | 4 |
\(=\)
| 1 | 1 | 1 | 1 |
| 1 | 4/3 | 1 | 3 |
| 1 | 1 | 2 | 2 |
| 5 | 1 | 1 |
Zróżnicowanie pierwszej reprezentacji \(T,\) równe \(\sqrt[9]{\frac{32}{9}},\) jest większe od zróżnicowania \(\sqrt[9]{\frac{24}{9}}\) drugiej reprezentacji. Tak więc pierwsza nie jest reprezentacją optymalną.
Okazuje się, że w tym wypadku druga reprezentacja jest optymalna.
Warunek konieczny jest również dostateczny, gdy \(T\) lub jej transpozycja jest rozmiaru \(2\times n,\) \(3\times4,\) \(4\times4,\) \(4\times5\) lub \(4\times6.\) Dla pozostałych rozmiarów warunki dostateczne sformułował Johannes Kemperman [3].
Dla tabeli koloru oczu i włosów tabela resztowa optymalnej reprezentacji ma następującą postać:
| WŁOSY | OCZY | |||
| brązowe | niebieskie | szare | zielone | |
| czarne | 2,302 | 0,959 | 1,035 | 0,480 |
| szatynowe | 1,044 | 1,043 | 0,966 | 0,721 |
| rude | 0,958 | 0,887 | 1,052 | 1,463 |
| blond | 0,214 | 4,068 | 0,623 | 1,387 |
Jej indeks równy 1,486 świadczy o bardzo wysokiej zależności między tymi kolorami. Prominentnymi oznakami tej zależności są pary włosy blond–oczy brązowe o wskaźniku zróżnicowania \(0{,}214^{-1}=4{,}673\) i włosy blond–oczy niebieskie o wskaźniku 4,068.
Analiza statystyczna tabeli danych.
Dane zapisane w tabeli opisują relację pomiędzy zmiennymi w jej wierszach i w kolumnach. Jeżeli tabela jest tabliczką mnożenia, to w zależności od sposobu zbierania danych możliwe są dwie interpretacje tej relacji:
Jeśli wiersze odpowiadają pewnym rozkładom prawdopodobieństwa a kolumny – ich możliwym do uzyskania wartościom (lub odwrotnie), to wnioskujemy o równości tych rozkładów;
Jeśli wiersze odpowiadają możliwym wartościom jednej zmiennej, a kolumny – drugiej, to wnioskujemy o ich niezależności.
Gdy tabela danych istotnie różni się od każdej tabliczki mnożenia, to hipotezy te powinny być odrzucone. Aby to się stało, wystarczy, by tabela istotnie różniła się od jej optymalnej reprezentacji, czego miarą jest indeks tabeli. Indeks ten ma interpretację statystyczną, podobnie jak wartości zróżnicowań \(z(r_{ij},1)\) tabeli resztowej. Ich istotnie duże wartości wskazują na związek między poziomem \(i\) zmiennej wierszowej i poziomem \(j\) zmiennej kolumnowej.
Wartości indeksu większe od 1,10 można uznać za umiarkowanie istotne, większe od 1,16 za istotne, a większe od 1,22 za bardzo istotne.
Infografika.
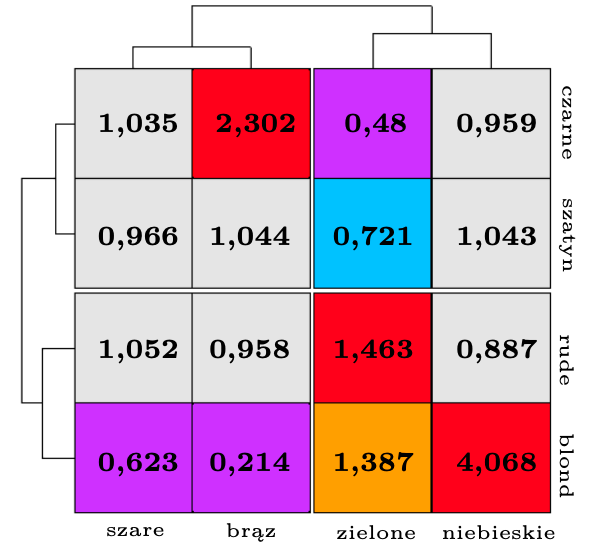
Tabelę resztową \(R\) można zabarwić według statystycznej istotności jej elementów. Kolory zimne, od fioletowego do jasnoniebieskiego, oznaczają małe reszty, a ciepłe – od czerwonego do żółtego – duże. Kolor szary odpowiada nieistotnie różniącej się od 1 wartości w tabeli \(R.\) Relacje łączące czynniki wierszowe czy kolumnowe ujawnia algorytm klasyfikacji, który porządkuje wiersze i kolumny tabeli \(R\) tak, aby sąsiadami były podobne wiersze/kolumny, a istotność różnicy między grupami można odczytać z długości gałęzi dendrytu, umieszczonego u góry i z lewej strony tabeli.
Przeanalizujmy w ten sposób tabelę dotyczącą koloru oczu/włosów.
Przedstawiona na marginesie tabela szybko prowadzi nas do następujących wniosków:
Kolor włosów tworzy dwie grupy: włosy jasne (rude i blond) oraz ciemne (czarne i szatyn).
Kolor oczu tworzy dwie grupy (oczy niebieskie i zielone oraz brązowe i szare).
Oczy niebieskie w sposób bardzo istotny (\(r = 4{,}068\)) są nadreprezentowane wśród blondynów; z pozostałym kolorem włosów nie są istotnie powiązane.
Włosy czarne są nadreprezentowane (\(r = 2{,}302\)) wśród osób o brązowym kolorze oczu, a wyjątkowo rzadko (\(r = 0{,}48\)) występują wśród osób o zielonych oczach.
Włosy jasne kojarzą się z oczami niebieskimi i zielonymi, a nie kojarzą się z oczami czarnymi i brązowymi.
Wspomnijmy na koniec, że te obserwacje znajdują częściowe biologiczne wytłumaczenie. Kolory oczu i włosów zależą od typu melaniny. Ciemne włosy często kojarzą się z ciemnymi oczami w populacjach, w których przeważa eumelanina. Feomelanina odpowiada za jasny kolor oczu i włosów.
Literatura
Campbell-Kelly, M. (edytor) i inni, The history of mathematical tables, Oxford University Press, Oxford 2007.
Dąbrowski, A., Przypadek wróg czy sojusznik?, Wiad. Mat. 56(2) 2020, 241–255.
Kemperman, J.H.B., Least absolute value and median polish, Inequalities in Statistics and Probability, IMS Lecture Notes Monograph Series, vol. 5 (1964), 84–103.