Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
XXVIII Dolnośląski Festiwal Nauki – „Nauka jest chrobra”
Tegoroczna, XXVIII edycja Dolnośląskiego Festiwalu Nauki odbywa się pod hasłem „Nauka jest chrobra”, które nawiązuje do 1000-lecia koronacji Bolesława Chrobrego – pierwszego króla Polski – i symbolicznie łączy odwagę władcy z odwagą poznawczą, jakiej wymaga podejmowanie wyzwań naukowych we współczesnym świecie. Hasło to stanowi również wyraz dumy z lokalnego dziedzictwa Dolnego Śląska i znaczenia nauki jako czynnika rozwoju społecznego.
Edycja wrocławska (13–21 września 2025) zainauguruje Festiwal serią wydarzeń na terenie największych wrocławskich uczelni. Szczególnym akcentem będzie Miasteczko Naukowe – wielki popularnonaukowy piknik edukacyjny, który po raz pierwszy odbędzie się na terenie Papieskiego Wydziału Teologicznego we Wrocławiu. Stoiska, eksperymenty, pokazy, warsztaty i atrakcje dla całych rodzin pokażą naukę w działaniu i w dostępnej formie.
Edycja regionalna (25 września– 31 października 2025) obejmie ponad 10 miast Dolnego Śląska – od Legnicy przez Głogów, Jelenią Górę i Zgorzelec po Kłodzko i Ząbkowice Śląskie. Lokalne ośrodki akademickie i instytucje kultury zaproszą do wspólnego odkrywania nauki w kontekście regionalnym.
W ramach całego Festiwalu zaplanowano ponad 1800 bezpłatnych wydarzeń: wykładów, pokazów, debat, warsztatów, spacerów naukowych i spotkań z naukowcami. To największe święto nauki na Dolnym Śląsku, otwarte dla wszystkich – od przedszkolaków po seniorów.
Część Czytelników po przeczytaniu tytułu tego artykułu pomyślała z pewnością, że to jakiś żart. W zaokrąglaniu liczb nie ma żadnej filozofii – jeśli chcę zaokrąglić liczbę do \(k\) miejsc po przecinku, to patrzę na cyfrę na pozycji \((k+1)\)-szej i jeśli jest ona mniejsza niż \(5,\) to ucinam wszystkie cyfry za pozycją \(k\)-tą, a w przeciwnym przypadku dodaję \(1\) na pozycji \(k\)-tej, również pomijając resztę zapisu. Od tej zasady są wprawdzie wyjątki – lubimy zaokrąglać w górę rzeczy, które o nas dobrze świadczą (np. średnią ocen) albo kiedy liczymy się z jakimś ryzykiem (np. błędy pomiaru). Wysyłając stolarzowi wymiary wnęki na szafę, raczej zaokrąglimy je w dół, gdyż odrobinę za szeroki mebel jest znacznie bardziej problematyczny niż odrobinę za wąski. Niemniej jednak, każdy wie, o co chodzi, więc możemy zakończyć artykuł w tym miejscu.
Niestety, mimo że wiedza o zaokrąglaniu i jego konsekwencjach jest powszechna, cały czas ta procedura prowadzi do pewnych niejasności.
| Prawdziwe wartości | 34.6 | 31.6 | 15.6 | 12.6 | 8.6 |
| Po zaokrągleniu | 35 | 32 | 16 | 13 | 9 |
Przed zaokrągleniem suma wynosiła \(100.0,\) a po zaokrągleniu \(102.0.\)
„Dlaczego odpowiedzi ankietowanych dodają się w sumie do \(102\%\)?” – możemy usłyszeć, kiedy ktoś chce podważyć wyniki pewnej sondy, najczęściej sondażu wyborczego, w którym jego ulubiona partia wypadła poniżej oczekiwań.
Powstaje więc pytanie, w jaki sposób zaokrąglić \(n\) liczb sumujących się do określonej wartości \(S\) tak, żeby po zaokrągleniu ich suma nadal wynosiła \(S.\) Warto zauważyć, że rozwiązanie tego problemu ma dużo szersze zastosowania, w szczególności kiedy musimy rozdzielić niepodzielne zasoby. Najbardziej oczywistym przykładem takiej sytuacji są wybory do wszelkiej maści ciał kolegialnych (np. sejmu), kiedy nie możemy przypisywać startującym tam komitetom ułamkowych miejsc (nie można zostać połową posła).
Funkcje zaokrąglające
Najogólniej funkcję zaokrąglającą możemy zdefiniować poprzez ciąg takich wartości \(s = s_0, s_1, s_2, \ldots,\) że \(k \le s_k \le k + 1.\) Wtedy funkcja zaokrąglająca \(r_s\) odpowiadająca takiemu ciągowi \(s\) przypisuje każdej liczbie \(x \in \mathbb{R}_+\) jej zaokrąglenie, to znaczy, jeśli \(x \in [k, k+1),\) to \[\begin{cases} r_s(x) = k & \text{jeśli } x \le s_k; \\ r_s(x) = k+1 & \text{jeśli } x > s_k. \end{cases}\] Przyjęliśmy tutaj dość arbitralnie, że w przypadku gdy \(x = s_k,\) zaokrąglamy do \(k,\) a nie \(k + 1.\) Nie jest to jednak nic istotnego w dalszych rozważaniach, ale upraszcza analizę.
Szczególnym przykładem funkcji zaokrąglających są funkcje stacjonarne \(r_q\) dla \(0 \le q \le 1.\) Funkcja stacjonarna \(r_q\) definiowana jest przez ciąg \(s_k = k + q\) dla każdego \(k.\) Zauważmy, że funkcja \(r_0\) to zwykłe zaokrąglanie w górę, \(r_1\) to zaokrąglanie w dół, a \(r_{1/2}\) to wspomniane na początku artykułu zaokrąglanie do najbliższej liczby całkowitej.
Metody mnożnikowe
Nasz oryginalny problem dotyczący zaokrąglania sondażowych wyników najłatwiej analizować, zakładając, że mamy dane \(n\) nieujemnych liczb \(x_1, x_2, \ldots, x_n\) sumujących się do \(1\) oraz pewną liczbę \(S.\) Naszym celem jest znalezienie takich \(n\) liczb całkowitych \(y_1, y_2, \ldots, y_n,\) że \(y_1 + y_2 + \ldots + y_n = S\) oraz \(y_i\) jest w jakimś sensie zaokrągleniem \(x_i \cdot S.\)
Ogólnie taki problem można rozwiązywać przy użyciu metod mnożnikowych. Dla dowolnej funkcji zaokrąglającej \(r,\) ciągu nieujemnych liczb \(x = (x_1, x_2, \ldots, x_n)\) sumujących się do \(1\) oraz liczby \(S\) możemy zdefiniować dopuszczalne zaokrąglenia jako: \[\begin{gathered} M_r(x, S) = \Bigl\{ (y_1, \ldots, y_n) \in \mathbb Z^n : \sum_{i=1}^n y_i = S \text{ oraz istnieje } \nu > 0 \text{ spełniające } y_i = r(x_i\cdot \nu) \Bigr\}. \end{gathered}\] Innymi słowy, skalujemy wszystkie liczby \(x_1, \ldots, x_n\) z pewną stałą (mnożnikiem) \(\nu > 0,\) zaokrąglamy je zgodnie z regułą \(r,\) a uzyskany wynik uznajemy za dobry, jeśli suma zaokrągleń wynosi \(S.\)
Łatwo wykazać, że dla dowolnych \(r_q, x, S\) zbiór \(M_{r_q}(x, S)\) ma co najwyżej jeden element, ale w niektórych przypadkach może być pusty. Na przykład przy zaokrąglaniu w dół \(r_1\) i danych \(x_1 = 1/3, x_2 = 2/3\) oraz \(S = 2,\) biorąc \(\nu < 3,\) będziemy mieli \(r_1(1/3 \cdot \nu) + r_1(2/3 \cdot \nu) \le 1,\) a dla \(\nu \ge 3\) zachodzi \({r_1(1/3 \cdot \nu) + r_1(2/3 \cdot \nu) \ge 3}.\)
Metody mnożnikowe są dość popularne w zastosowaniach praktycznych. Na przykład metoda d’Hondta, stosowana w wyborach do polskiego sejmu, jest metodą mnożnikową korzystającą z zaokrągleń w dół (czyli \(r_1\)). Dla przykładu przeanalizujmy wyniki w ostatnich wyborach do sejmu, w 2023 roku, w okręgu numer 19 (obejmującym miasto Warszawę). Można było tam głosować na \(7\) komitetów wyborczych, z których \(5\) przekroczyło próg wyborczy i brało udział w podziale \(20\) mandatów. Komitety te otrzymały (w kolejności malejącej) \(741 286,\) \(345 380,\) \(230 648,\) \(227 127\) i \(124 220\) głosów. Dzieląc te liczby przez sumę wszystkich głosów oddanych na komitety, które przekroczyły próg wyborczy (czyli \(1 668 661\)), otrzymujemy \(x = (0.444, 0.207, 0.138, 0.136, 0.074).\) Aby obliczyć podział mandatów, musimy znaleźć \(M_{r_1}(x, 20).\) Czytelnik zechce sprawdzić, że w tym celu można wziąć dowolną wartość \(\nu\) z przedziału (z dokładnością do nomen omen zaokrąglenia) \((22.04, 22.51),\) i każda z nich da ten sam podział mandatów. Dla przykładu, biorąc \(\nu = 22.3\) i skalując przez nie wektor \(x,\) otrzymamy \((9.91, 4.62, 3.08, 3.04, 1.66),\) a po zaokrągleniu tych liczb w dół dostajemy podział mandatów \((9, 4, 3, 3, 1).\) Czytelnik Wnikliwy zechce sprawdzić, że te wyliczenia pokrywają się z oficjalnymi wynikami wyborów podanymi na stronie Państwowej Komisji Wyborczej.
Problem znalezienia odpowiedniego mnożnika \(\nu\) nie wydaje się zbyt skomplikowany dla konkretnych danych wejściowych. Przy za małym \(\nu\) wartości \(r(x_i \cdot \nu)\) będą sumować się do wartości mniejszej niż \(S,\) a przy \(\nu\) za dużym – do wartości większej niż \(S.\) W związku z tym możemy nasze \(\nu\) eksperymentalnie zwiększać lub zmniejszać, aż znajdziemy odpowiednią wartość.
Sytuacja komplikuje się, kiedy nie znamy dokładnych wartości \(x_1, \ldots, x_n.\) Jest to typowy problem z przeliczaniem wyników sondażowych na faktyczny podział mandatów w polskim sejmie. Zauważmy, że publikowane sondaże pokazują szacunkowe poparcie komitetów wyborczych w skali całego kraju, ale podział mandatów odbywa się w poszczególnych okręgach wyborczych, różniących się ilością przydzielanych mandatów, a nierzadko także preferencjami wyborców, mogącymi znacząco odbiegać od ogólnokrajowej średniej. Jak w takim razie przeliczyć wyniki sondażowe na faktyczny podział mandatów? W tym celu musimy sięgnąć po aparat rachunku prawdopodobieństwa.
Losowe wartości
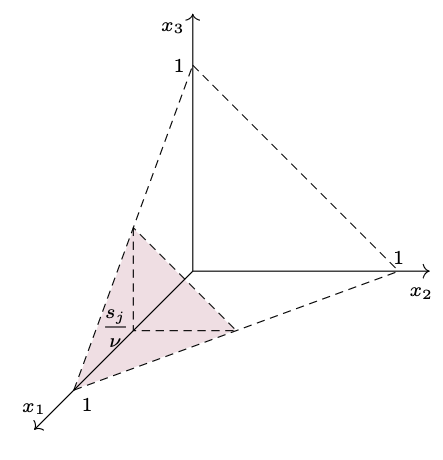
Niech \(X = (X_1, X_2, \ldots, X_n)\) będzie wektorem losowym o rozkładzie jednostajnym na zbiorze \(\mathcal S_{n - 1} = \{(x_1, \ldots, x_n) \in \mathbb{R}_+ : \sum_{i = 1}^n x_1 = 1\}\) nazywanym \((n{-}1)\)-wymiarowym sympleksem. Na przykład dla \(n=3\) wektor \((X_1,X_2,X_3)\) to punkt losowo (jednostajnie) wybrany z trójkąta o wierzchołkach \((0,0,1), (0,1,0)\) i \((1,0,0).\) Ponieważ liczby \(X_1, \ldots, X_n\) sumują się do \(1,\) więc możemy je interpretować jako proporcje głosów oddanych na poszczególne komitety wyborcze w danym okręgu. Dla danej wartości \(\nu\) zdefiniujmy \[T_n(\nu) = \sum_{i = 1}^n r(X_i\cdot \nu),\] czyli sumę \(n\) losowych liczb \(X_1, \ldots, X_n\) przeskalowanych przez \(\nu\) i zaokrąglonych zgodnie z regułą \(r.\) Wykażemy, że jeśli reguła zaokrąglania \(r\) dana jest przez ciąg \(s_0, s_1, \ldots,\) to \[\operatorname{\mathbb E} T_n(\nu) = n \sum_{j = 0}^k \left(1 - \frac{s_j}\nu \right)^{n - 1},\] gdzie \(k\) jest największym indeksem, dla którego \(s_k \le \nu.\)
Dowód. Niech \(N_1 = r(\nu X_1).\) Z liniowości wartości oczekiwanej mamy \({\operatorname{\mathbb E} T_n(\nu) = n \operatorname{\mathbb E} N_1}.\) Dla danej liczby całkowitej \(j \le k\) zachodzi \(N_1 > j\) wtedy i tylko wtedy, gdy \(X_1 > s_j/\nu.\) Pozostawiamy Czytelnikowi sprawdzenie, że \(\mathbb P(N_1 > j) = \mathbb P(X_1 > s_j/\nu) = (1 - s_j/\nu)^{n - 1},\) co w szczególności daje nam \[\operatorname{\mathbb E} T_n(\nu) = n \operatorname{\mathbb E} N_1 = n \sum_{j = 0}^k \mathbb P(N_1 > j) = n \sum_{j = 0}^k \left(1 - \frac{s_j}\nu \right)^{n - 1}.{\Box}\] Nietrudno zauważyć, że funkcja \(f(\nu) = n \sum_{j = 0}^k \left(1 - {s_j}/\nu \right)^{n - 1}\) jest funkcją ciągłą na przedziale \((0, \infty)\) i rosnącą względem \(\nu,\) a więc dla ustalonych \(S\) i \(n\) istnieje jedyne takie \(\nu,\) że \(\operatorname{\mathbb E} T_n(\nu) = S.\)
Bibliografia
D. Boratyn, W. Słomczyński, D. Stolicki, Seat Allocation and Seat Bias under the Jefferson–D’Hondt Method, arXiv:1805.08291.
J. Flis, W. Słomczyński, D. Stolicki, Pot and Ladle: A Formula for Estimating the Distribution of Seats under the Jefferson-D’Hondt Method.
Happacher, M., and Pukelsheim, F. (2000), Rounding probabilities: Maximum probability and minimum complexity multipliers, Journal of Statistical Planning and Inference, 85(1–2), 145–158.
Jasne jest, że dla każdej stacjonarnej funkcji zaokrąglającej \(r_q\) zachodzi \({\nu X_i - q \le r_q(\nu X_i) \le \nu X_i + 1 - q}.\) Sumując te nierówności, dostajemy \({\nu - nq \le T_n(\nu) \le \nu + n(1 - q)}.\) Biorąc \(\nu = S + n(q - 1/2),\) dostajemy symetryczne ograniczenia: \[S - n/2 \le T_n(S + n(q - 1/2)) \le S + n/2.\] Niezbyt skomplikowana, ale dość długa analiza pokazuje, że dla dowolnego \(\nu\) zachodzi \[\operatorname{\mathbb E} T_n(\nu) = \nu - n(q - 1/2) + \mathcal O(1/\nu),\] więc dla \(\nu_S = S + n(q - 1/2)\) mamy \[\operatorname{\mathbb E} T_n(\nu_S) = S + \mathcal O(1/S),\] co oznacza, że dla dużych wartości \(S\) wartość oczekiwana \(T_n(\nu_S)\) jest bliska \(S.\) Daje nam to intuicję, że używanie \(\nu_S\) jako mnożnika daje nam dobre przybliżenie podziału mandatów.
Sondaże (nie) kłamią
Wróćmy więc do postawionego chwilę temu pytania: Jak przeliczyć ogólnokrajowe wyniki sondażowe na faktyczny podział mandatów? Nie znamy dokładnych wartości poparcia każdej partii w każdym okręgu, a tylko liczbę okręgów (w Polsce w wyborach do sejmu jest ich \(o = 41\)), liczbę wszystkich mandatów (do sejmu wybieramy \({M = 460}\) posłów) oraz liczbę komitetów, które przekroczyły próg wyborczy (w ostatnich wyborach było to \(n = 5\)). W każdym z \(o\) okręgów wybieramy średnio \(S = M/o\) posłów, więc przyjmując mnożnik \(\nu_S = S + n(q - 1/2),\) partia, która uzyskała \(p_i\)-tą część ważnych głosów w skali kraju, powinna otrzymać w każdym okręgu mniej więcej \(r_1(p_i \cdot \nu_S)\) mandatów. Jeśli przyjmiemy, że średnia wartość części ułamkowej \(p_i \cdot \nu_S\) to \(1/2\) (bo pochodzi ona z odcinka \((0, 1)\)), to tyle średnio będziemy „tracili” na zaokrąglaniu w dół. W związku z tym otrzymujemy, że \(i\)-ta partia otrzyma \[(p_i \cdot (S + 1/2 \cdot n) - 1/2) \cdot o = p_i \cdot (M + 1/2 \cdot n \cdot o) - o/2\] mandatów w skali kraju. Możemy ten wzór interpretować w ten sposób, że każda partia dostaje \(p_i M\) mandatów, a następnie oddaje \(o/2\) mandatów do puli, która znowu zostaje podzielona. Jeśli próg wyborczy przekroczyło \(n\) komitetów, to w dodatkowej puli mamy \(1/2 \cdot n \cdot o\) mandatów, z których otrzymujemy \(p_i\)-tą część.
Aby wyprowadzić powyższy wzór, musieliśmy przyjąć dość dużo założeń i uproszczeń. Okazuje się jednak, że w praktyce sprawdza się dość dobrze, co można zobaczyć na przykładzie ostatnich wyborów do sejmu w Polsce.
| Komitet | Głosy | Część głosów ważnych | Przewidywane | Faktyczne |
|---|---|---|---|---|
| PiS | 7 640 854 | 0.3676 | 186.26 | 194 |
| KO | 6 629 402 | 0.3189 | 158.89 | 157 |
| TD | 3 110 670 | 0.1496 | 63.67 | 65 |
| NL | 1 859 018 | 0.0894 | 29.80 | 26 |
| Konf | 1 547 364 | 0.0744 | 21.37 | 18 |
Dodajmy, że wzór ten został przedstawiony w pracy [2], a jego matematyczna słuszność przy pewnych założeniach na temat systemu wyborczego została udowodniona w pracy [1]. Analizując ten wzór, możemy też zobaczyć, na czym polega faworyzowanie większych partii w systemie wyborczym stosowanym w Polsce.
Na koniec warto dodać, że metoda d’Hondta jest stosowana w Polsce także do wyborów do sejmików województw, rad powiatów i większych rad gmin. Zachęcam Czytelników do sprawdzenia w swojej Małej Ojczyźnie, na ile faktyczny podział mandatów w tych organach samorządowych pokrywa się z tymi przewidywanymi przez podany wyżej wzór.