Redaguje Marcin E. KUCZMA
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
893 (\(WT = 3{,}25\)) i 894 (\(WT = 1{,}35\))
z numeru 1/2025
Andrzej Kurach Ryjewo 47,81 Janusz Olszewski Warszawa 45,27 Krzysztof Zygan Lubin 44,74 Michał Warmuz Żywiec 41,39 Marcin Kasperski Warszawa 40,49 Marek Spychała Warszawa 39,84 Piotr Wiśniewski Warszawa 38,24 Grzegorz Wiączkowski 37,93 Andrzej Daniluk Warszawa 37,89 Krzysztof Kamiński Pabianice 35,71 Marian Łupieżowiec Gliwice 35,53 Krzysztof Maziarz Londyn 34,67 Jerzy Cisło Wrocław 33,16 I znów: na linii mety – dobrze znane nazwiska: pan Andrzej Kurach po raz czwarty; pan Janusz Olszewski po raz dwudziesty piąty; pan Krzysztof Zygan po raz drugi. Czekamy na kolejne okrążenia!
Rozwiązania zadań z numeru 4/2025
Przypominamy treść zadań:
899. Niech \({g\colon\mathbb Z^2\to\mathbb R}\) będzie dowolną funkcją (\(\mathbb Z^2\) jest zbiorem punktów kratowych, czyli uporządkowanych par liczb całkowitych). Określamy odległość punktów \({P,Q\in\mathbb Z^2},\) \({P=(x,y)},\) \({Q=(u,v)}\) wzorem \({d(P,Q)=\max(|x-u|,|y-v|)}.\) Dowieść, że istnieje nieskończenie wiele pięcioelementowych zbiorów takich punktów kratowych \((P_0,P_1,P_2,P_3,P_4),\) że (dla \({i=1,2,3,4}\)): \({d(P_0,P_i)=1},\) \({g(P_0)\le{g(P_i)}}.\)
900. Wielomiany \(f_1,f_2,f_3,f_4\) jednej zmiennej, o współczynnikach rzeczywistych, spełniają warunki: \[\begin{aligned} f_1(x)\le f_2(x)\le f_3(x)\le f_4(x)\ \ \ & \hbox{dla}\;x\in[0,1], \\ f_2(x)\le f_4(x)\le f_1(x)\le f_3(x)\ \ \ & \hbox{dla}\;x\in[-1,0]. \end{aligned}\] Wykazać, że \({f_1=f_2=f_3=f_4}.\)
899. O punktach \(P,Q\) z odległością \({d(P,Q)=1}\) będziemy mówili, że sąsiadują. Weźmy dowolny kwadrat złożony z 16 punktów kratowych (po cztery w czterech rządkach). Odetnijmy punkty narożne. Zostaje układ \(K\) złożony z 12 punktów (kolejno w rządkach: \(2,4,4,2\)). W tym układzie każdy punkt ma co najmniej czterech sąsiadów.
Bierzemy jako \(P_0\) ten punkt zbioru \(K,\) w którym funkcja \(g\) przyjmuje najmniejszą wartość. Niech \(P_1,P_2,P_3,P_4\) będą punktami zbioru \(K,\) sąsiadującymi z \(P_0\) (gdy jest ich więcej, wybieramy cztery dowolne). Piątka \(P_0,P_1,P_2,P_3,P_4\) ma wymaganą własność.
Na płaszczyźnie kratowej możemy umieścić nieskończenie wiele kopii zbioru \(K\) i w każdym z nich znaleźć piątkę punktów, o jaką chodzi.
900. Oznaczenia przedziałów: \({I=[0,1]},\) \({J=[-1,0]}.\) Dowód tezy zadania nie wprost. Przypuśćmy, że nie wszystkie cztery wielomiany są identyczne. Z podanych warunków wynika, że wówczas żadne dwa nie są identyczne. Zatem następujące trzy wielomiany są niezerowe: \[P=f_2-f_1 \begin{cases} \le0 & \text{w~$J$},\cr \ge0 & \text{w~$I$},\cr \end{cases} \ \ \ Q=f_3-f_1 \begin{cases} \ge0 & \text{w~$J$},\cr \ge0 & \text{w~$I$},\cr \end{cases} \ \ \ R=f_4-f_1 \begin{cases} \le0 & \text{w~$J$},\cr \ge0 & \text{w~$I$}.\cr \end{cases}\] Jasne, że \({P(0)=Q(0)=R(0)=0}.\) O lokalnym zachowaniu tych trzech wielomianów w otoczeniu zera decydują ich składniki w najniższej potędze. Używając skrótu sws (\(=\) składniki wyższych stopni) możemy napisać: \[P(x)=ax^k+\hbox{sws},\ \ \ Q(x)=bx^l+\hbox{sws},\ \ \ R(x)=cx^m+\hbox{sws}\] (\(k,l,m\) to wykładniki owych wiodących składników; \(a,b,c\) – współczynniki). Wielomiany \(P\) i \(R\) zmieniają znak przy przejściu przez 0 i wobec tego wykładniki \(k\) i \(m\) są nieparzyste; natomiast \(Q\) ma lokalne minimum w punkcie 0, zatem wykładnik \(l\) jest parzysty (tak więc \({k\ne{l}\ne{m}}\)).
Wielomian \(P-Q=f_2-f_3 \begin{cases} \le0 & \text{w~$J$},\cr \le0 & \text{w~$I$}\cr \end{cases}\) ma lokalne maksimum w punkcie 0, co (wobec wiedzy, że \({k\ne{l}}\)) oznacza, że \(\min\{k,l\}\) jest liczbą parzystą. Stąd, na mocy wcześniejszych ustaleń, \({k>l}.\)
Wielomian \(Q-R=f_3-f_4 \begin{cases} \ge0 & \text{w~$J$},\cr \le0 & \text{w~$I$}\cr \end{cases}\) zmienia znak przy przejściu przez 0, co teraz oznacza, że \(\min\{l,m\}\) jest liczbą nieparzystą. Stąd \({l>m}\) (i w konsekwencji \({k>m}\)).
Wreszcie wielomian \(R-P=f_4-f_2 \begin{cases} \ge0 & \text{w~$J$},\cr \ge0 & \text{w~$I$}\cr \end{cases}\) ma lokalne minimum w punkcie 0, co oznacza, że \(\min\{k,m\}\) (czyli po prostu \(m\)) jest liczbą parzystą. Ale wcześniej zostało ustalone, że \(m\) jest liczbą nieparzystą. Sprzeczność kończy dowód.
Redaguje Elżbieta ZAWISTOWSKA
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
790 (\(WT=2{,}32\)), 791 (\(WT=2{,}92\))
z numeru 1/2025
Jacek Konieczny Poznań 41,11 Jan Zambrzycki Białystok 4 – 33,80 Andrzej Nowogrodzki Chocianów 3 – 29,48
Rys. 1
Rys. 2
Rys. 3
Rozwiązania zadań z numeru 4/2025
Przypominamy treść zadań:
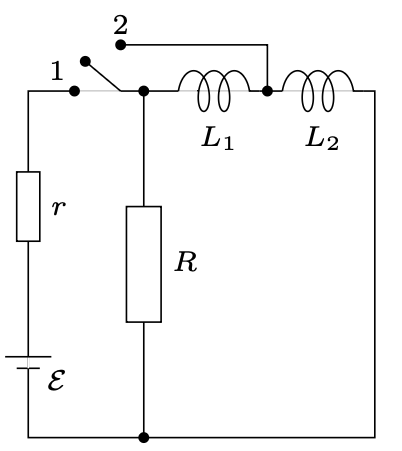
796. W obwodzie przedstawionym na rysunku 1 klucz zamknięto do położenia 1, a po ustaleniu się prądów bardzo szybko przełączono go do pozycji 2. Przyjmując, że cewki \(L_1\) i \(L_{2}\) są idealne, wyznaczyć ilość ciepła, jaka wydzieli się na oporniku \(R\) po przełączeniu. Siła elektromotoryczna źródła wynosi \(\mathcal E ,\) jego opór wewnętrzny \(r.\)
797. W środku dna prostopadłościennej barki o długości \(a=80\) m, szerokości \(b=10\) m i wysokości \(c=5\) m powstał otwór o średnicy \(d=1\) cm. Ocenić czas, po którym barka zatonie, jeśli nie będzie odpompowywana z niej woda. Barka jest otwarta z góry, nie ma żadnego ładunku, początkowa wysokość burty nad poziomem wody wynosi \(h=3{,}75\) m.
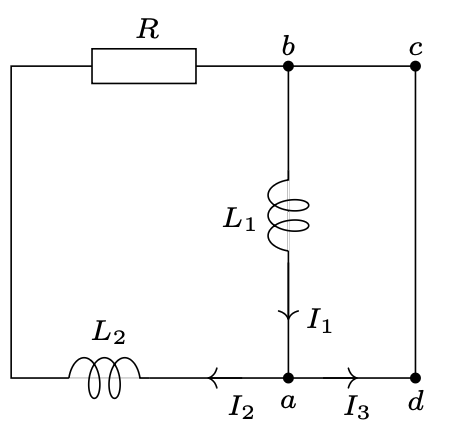
796. Przed przełączeniem klucza przez cewki \(L_1\) i \(L_2\) płynie prąd o natężeniu \(I={\mathcal E }/{r}.\) Ponieważ cewki są idealne, napięcie na oporniku \(R,\) a tym samym natężenie prądu płynącego przez ten opornik, są równe zeru. Natychmiastowe przełączenie klucza z położenia 1 do położenia 2 oznacza, że w trakcie przełączania natężenie prądu w cewkach praktycznie nie zmienia się. Układ w położeniu 2 przedstawiony jest na rysunku 2. Wielkości początkowe wynoszą: \[I_1\left(0\right)=I_2\left(0\right)=I={\mathcal E }/{r};\ \ \ I_3\left(0\right)=0.\] Z prawa Kirchhoffa dla konturu \(abcd\) w dowolnej chwili czasu mamy: \[L_1{dI_1}/{dt=0},\text{ stąd }I_1=\text{const}.\] Ponieważ \(I_1=I_2+I_3,\) zachodzi związek: \[{dI_1}/{dt}={dI_2}/{dt}+{dI_3}/{dt},\text{ stąd }dI_2=-dI_3.\] Na oporniku \(R\) wydziela się ciepło, co powoduje zanikanie prądu \(I_2,\) a jego zmniejszenie jest równe przyrostowi prądu \(I_3.\) Po ustaleniu się prądów mamy: \[I_1\left(\infty \right)=I_3\left(\infty \right)={\mathcal E }/{r}, I_2\left(\infty \right)=0.\] Zgodnie z zasadą zachowania energii, energia pola magnetycznego cewki \(L_2\) wydzieli się w postaci ciepła \(Q\) na oporniku \(R\): \[Q={L_2{I_2}^2\left(0\right)}/{2}={L_2{\mathcal E }^2}/{\left(2r^2\right)}.\]
797.
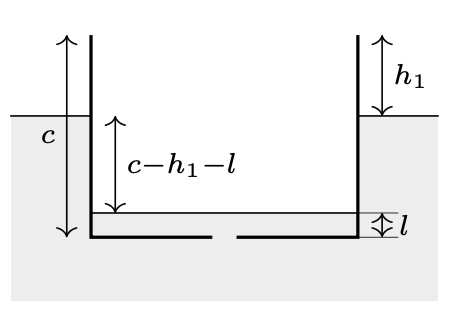
Warunek pływania barki, w której nie ma wody, ma postać: \[\tag{1} \label{GrindEQ__1_} mg=\rho gab(c-h),\] gdzie \(m\ \)jest masą barki, a \(\rho\) gęstością wody. Załóżmy, że barka zanurzyła się tak, że wysokość jej burty nad powierzchnią wody jest równa \(h_1,\) a grubość warstwy wody wewnątrz barki wynosi \(l\) (rys. 3). Warunek pływania przyjmuje teraz postać: \[\tag{2} \label{GrindEQ__2_} mg+\rho gabl=\rho gab(c-h_1).\] Z równań \(\eqref{GrindEQ__1_}\) i \(\eqref{GrindEQ__2_}\) otrzymujemy: \[\tag{3} \label{GrindEQ__3_} c-h_1-l=c-h,\] co oznacza, że różnica poziomów wody w dowolnej chwili (dopóki barka nie zatonie) jest stała i równa różnicy wysokości barki i wysokości burty nad wodą w nieprzeciekającej barce. Zatem woda dostaje się do barki ze stałą prędkością. Wyznaczymy ją, korzystając z równania Bernoulliego.Przyjmiemy, że energia potencjalna na poziomie wody na zewnątrz barki wynosi 0. Dla rurki prądu, która zaczyna się na poziomie wody na zewnątrz barki i kończy na poziomie wody wewnątrz barki nad otworem, możemy napisać: \[\tag{4} \label{GrindEQ__4_} p_0=p_0-\rho g\left(c-h_1-l\right)+{\rho v^2}/{2},\] gdzie \(p_0\) jest ciśnieniem atmosferycznym, \(v\) prędkością wody wciekającej do otworu. W równaniu \(\eqref{GrindEQ__3_}\) uwzględniliśmy fakt, że powierzchnia wody wewnątrz barki jest dużo większa od powierzchni otworu. Dlatego prędkość podnoszenia się wody w barce jest dużo mniejsza od \(v\) i można ją zaniedbać. Z równań \(\eqref{GrindEQ__3_}\) i \(\eqref{GrindEQ__4_}\) otrzymujemy: \(v=\sqrt{2g(c-h)}.\)
Barka zatonie, gdy krawędź burty zrówna się z powierzchnią wody na zewnątrz, czyli poziom wody nad podłogą osiągnie wartość \(h,\) a objętość wody w barce \[V=abh=Sv\Delta t,\text{ gdzie }S={\pi d^2}/{4}.\] Szukany czas: \[\Delta t={4abh}/{\left(\pi d^2\sqrt{2g\left(c-h\right)}\right)}\approx 3\text{ miesiące.}\]