Delta 8/2025

Zadania

Dominik Burek i Andrzej Majhofer

Zadanie M 1825

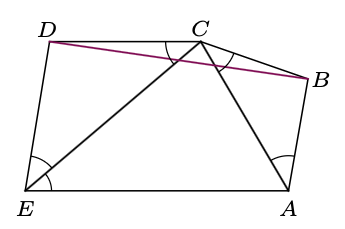
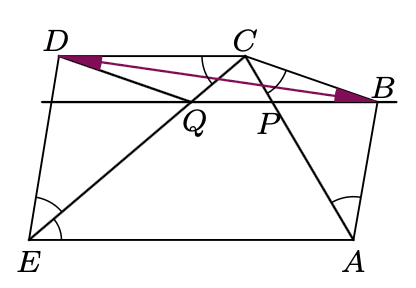
Dany jest pięciokąt wypukły \(ABCDE,\) w którym \[\measuredangle CAB=\measuredangle BCA=\measuredangle ECD=\measuredangle DEC=\measuredangle AEC.\] Udowodnić, że \(CE\) połowi \(BD.\)

image

Rozwiązanie
Z równości kątów mamy \(CD \!\!\parallel\!\! AE.\) Niech prosta przechodząca przez \(B\) i równoległa do \(AE\) przecina \(AC\) i \(CE\) odpowiednio w punktach \(P\) i \(Q.\) Zauważmy, że \(P\) i \(Q\) dzielą podstawy \(CA\) i \(CE\) podobnych trójkątów równoramiennych \(ABC\) i \(EDC\) w tym samym stosunku, więc \(\measuredangle CBP = \measuredangle CDQ.\) Wobec tego czworokąt \(BCDQ\) jest równoległobokiem, a środki odcinków \(BD\) i \(CQ\) oczywiście się pokrywają.

image

Zadanie M 1826

Na każdej z \(2n\) kart napisano pewną liczbę z przedziału \([1,2]\) (na różnych kartach napisano być może różne liczby). Udowodnić, że można te karty podzielić na dwa stosy tak, aby sumy liczb napisanych na kartach stosów \(s_1,\) \(s_2\) spełniały nierówności \[\frac{n}{n+1} \leq \frac{s_1}{s_2} \leq 1.\]

Rozwiązanie
Niech \(x_1 \leq x_2 \leq \ldots \leq x_{2n}\) będą liczbami zapisanymi na kartach. Udowodnimy, że \(s_1 = x_1 + x_3 + \ldots + x_{2n-1}\) oraz \(s_2=x_2+x_4+\ldots+x_{2n}\) spełniają warunki zadania. Nierówność \(s_1 \leq s_2\) jest oczywista. Rozważmy drugą nierówność \[\begin{aligned} \frac{s_1}{s_2} & \geq \frac{x_3 + x_5 \ldots + x_{2n-1} + 1}{x_2 + x_4 + \ldots + x_{2n-2} + 2}\geq \\ & \geq \frac{x_2 + x_4 + \ldots + x_{2n-2}+1}{x_2 + x_4 + \ldots + x_{2n-2} + 2}= \\ & =1-\frac{1}{x_2 + x_4 + \ldots + x_{2n-2} + 2} \geq \\&\geq 1-\frac{1}{n+1} = \frac{n}{n+1}. \end{aligned}\]
Zadanie M 1827

Dane są takie liczby pierwsze \(p,\) \(q,\) że \(p<q<2p.\) Udowodnić, że istnieją takie dwie kolejne liczby całkowite dodatnie, że największy dzielnik pierwszy jednej z nich jest równy \(p,\) a drugiej \(q.\)

Rozwiązanie
Liczby \(p\) i \(q\) są względnie pierwsze, więc istnieje takie \(1\leqslant a < q,\) że \(ap \equiv 1\pmod{q}.\) Rozpatrzmy teraz dwa przypadki.

  • Jeśli \(1\leqslant a \leqslant p,\) to rozpatrzmy dwie kolejne liczby: \(ap\) oraz \(ap-1.\) Ponieważ \(1\leqslant a\leqslant p,\) największym dzielnikiem pierwszym liczby \(ap\) jest \(p.\) Ponadto \(ap - 1 \leq p^2-1< q^{2},\) więc liczba całkowita \((ap-1)/q\) jest mniejsza od \(q,\) zatem żaden dzielnik pierwszy liczby \(ap - 1\) nie przekracza \(q.\)

  • Jeśli \(p < a < q,\) wtedy \((q - a)p \equiv -1\pmod{q}\) i \({1\leqslant q - a < q.}\) Rozpatrzmy teraz dwie kolejne liczby \((q - a)p\) oraz \((q - a)p + 1.\) Ponieważ \(q - p < p < a,\) więc \(q - a < p,\) a więc największym dzielnikiem pierwszym liczby \((q - a)p\) jest \(p.\) Z drugiej strony \((q - a)p + 1 < q^{2},\) zatem liczba całkowita \(((q - a)p + 1)/q\) jest mniejsza od \(q\) i podobnie jak w pierwszym przypadku żaden dzielnik pierwszy liczby \((q - a)p + 1\) nie przekracza \(q.\)

Zadanie F 1125

W chwili \(t_0\) w całej objętości jednorodnego, kulistego ciała niebieskiego o promieniu \(R\) następuje wybuch. W wyniku wybuchu cała masa zaczyna ekspandować. Początkowa prędkość \(v\) ekspansji każdego elementu masy jest proporcjonalna do jego odległości \(r\) od środka ciała: \(v = Hr.\) \(H > 0\) jest pewną stałą. Jaki warunek musi spełniać początkowa gęstość \(\rho\) ciała, żeby opisany wybuch zakończył się ponownym skupieniem całej masy? Stała grawitacji wynosi \(G.\)

Rozwiązanie
Zbadajmy ruch małego elementu masy \(\Delta m\) znajdującego się w chwili początkowej w odległości \(r\) od środka ciała. Element ten oddala się od środka ciała z prędkością \(v=Hr\) i jest przyciągany grawitacyjnie jedynie przez masę wypełniającą kulę o promieniu \(r.\) Masa znajdująca się w odległości od środka większej niż \(r\) ,,ucieka” z prędkością większą niż \(Hr\) i nie oddziałuje grawitacyjnie na \(\Delta m.\) Całkowita energia \(\Delta E\) elementu \(\Delta m\) wynosi: \[\begin{aligned} \Delta E & = - \frac{4\pi r^3\rho G\Delta m}{3r} + \frac{1}{2} \Delta m v^2 \\&= - \frac{4\pi r^3\rho G\Delta m}{3r} + \frac{1}{2} \Delta m H^2 r^2. \end{aligned}\] Ekspansja skończy się ponownym skupieniem (,,zapadnięciem”) masy, jeśli \(\Delta E < 0.\) Oznacza to, że ekspansja wyhamuje, po czym zakończy się ponownym skupieniem całej masy, jeśli początkowa gęstość masy ciała spełniała warunek: \[\rho > \frac{3H^2}{8\pi G}.\]
Zadanie F 1126

W upalny dzień temperatura w mieszkaniu wynosi \(t_p = 30\)C. Kompresor lodówki ma moc \(P = 40\) W. Jaki jest minimalny czas \(\tau\) potrzebny do zamrożenia (tzn. zamienienia w lód) \(m = 1\) kg wody o początkowej temperaturze \(t_w = 0\)C? Ciepło topnienia lodu \(L = 334\) J/g.

Rozwiązanie
Minimalną pracę potrzebną do zamrożenia wody obliczymy, porównując działanie kompresora z odwróconym cyklem Carnota – pobierającym ciepło od wody o temperaturze bezwzględnej \(T_1 = t_w + 273\) K i oddającym ciepło otoczeniu o temperaturze bezwzględnej \(T_2 = t_p + 273\) K (\(T_2 > T_1\)), wykonującym przy tym pracę \(W = P\tau.\) Ciepło pobrane \(Q_1 = Lm,\) a oddane \(Q_2 = Q_1 + W.\) Na podstawie II zasady termodynamiki wiemy, że spełniona jest nierówność Clausiusa: \[\frac{Q_1}{T_1} - \frac{Q_2}{T_2} \le 0,\] czyli (\(Q_2 = Q_1 + W\)): \[W = P\tau \ge \frac{T_2 - T_1}{T_1}Q_1 = \frac{T_2 - T_1}{T_1}Lm .\] Ostatecznie: \[\tau \ge \frac{(T_2 - T_1)Lm}{T_1P}.\] Liczbowo: \(\tau \ge 918\) s \(\approx\) 15,3 minuty.