Zadania z matematyki nr 905, 906 Termin nadsyłania rozwiązań: 30 XI 2025
Redaguje Marcin E. KUCZMA
905. Niech \(f(x)=x^3(x^2+1)^{-1}.\) Wyznaczyć wszystkie możliwe całkowite wartości sumy \({f(a)+f(b)+f(c)}\) dla dowolnych liczb całkowitych dodatnich \(a,b,c.\)
906. W przestrzeni (trójwymiarowej) dana jest parabola \(P.\) Niech \(R\) będzie zbiorem wszystkich punktów będących wierzchołkami stożków obrotowych, na których leży \(P\) [przez stożek obrotowy rozumiemy tu powierzchnię powstałą przez obrót prostej wokół przecinającej ją (nie prostopadle) innej prostej (osi obrotu)].
Udowodnić, że zbiór \(R\) także jest parabolą oraz wyjaśnić, jak są usytuowane jej wierzchołek i ognisko względem wierzchołka i ogniska paraboli \(P.\) [Wierzchołek paraboli to punkt jej przecięcia z płaszczyzną symetrii; ognisko to punkt (w jej płaszczyźnie) określony przez własność: każdy punkt paraboli jest jednakowo odległy od ogniska i od pewnej prostej (zwanej kierownicą)].
Zadanie 906 zaproponował pan Janusz Fiett z Warszawy.
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
895 (\(WT = 1{,}73\)) i 896 (\(WT = 1{,}65\))
z numeru 2/2025
Michał Warmuz Żywiec 44,77 Marek Spychała Warszawa 43,22 Marcin Kasperski Warszawa 42,22 Piotr Wiśniewski Warszawa 41,62 Grzegorz Wiączkowski 41,31 Andrzej Daniluk Warszawa 39,54 Krzysztof Maziarz Londyn 38,05 Krzysztof Kamiński Pabianice 36,87 Jerzy Cisło Wrocław 36,37 Marian Łupieżowiec Gliwice 35,53 Roksana Słowik 31,78 Pan Michał Warmuz: nowa twarz w Klubie 44 M – pierwsza od przeszło roku. Witamy!
Rozwiązania zadań z numeru 5/2025
Przypominamy treść zadań:
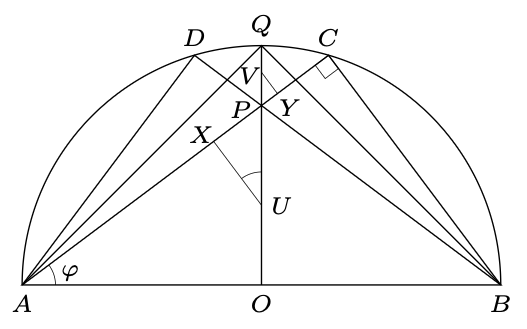
901. Trapez równoramienny \(ABCD\) jest wpisany w okrąg \(\Omega\) o średnicy \(AB.\) Przekątne trapezu, długości \(d,\) przecinają się w punkcie \(P.\) Okrąg styczny do odcinków \(PC,\) \(PD\) i do krótkiego łuku \(CD\) (okręgu \(\Omega\)) ma promień \(r.\) Okrąg wpisany w trójkąt \(ABP\) ma promień \(3r.\) Obliczyć stosunek \({r/{d}}.\)
902. Dla liczby naturalnej \(n\) niech \(w(n)\) oznacza największy całkowity wykładnik, dla którego \(n!\) dzieli się przez \(10^{w(n)}\) i niech \({f(n)=10^{-w(n)}n!}.\) Udowodnić, że dla każdej liczby naturalnej \(m\) spełniona jest zależność \({f(5^m)\equiv2^m}\) (mod 5).
901. Niech \(V\) i \(U\) będą (odpowiednio) środkami okręgów o promieniach \(r\) i \(3r,\) określonych w zadaniu. Nazwijmy punkty styczności: okrąg \((U,3r)\) styczny do odcinka \(AB\) w punkcie \(O\) (środku okręgu \(\Omega\)) i do odcinka \(AP\) w punkcie \(X\); okrąg \((V,r)\) styczny do łuku \(CD\) w jego środku \(Q\) i do odcinka \(CP\) w punkcie \(Y.\) Niech \({R=OA=OB=OQ}.\)
Skoro \({UX=3r},\) \({VY=r},\) zatem z podobieństwa \({\triangle{PXU}\sim\triangle{PYV}}\) odczytujemy, że \({PU/{PV}=3},\) i w konsekwencji \({PO/{PQ}=3}.\) Stąd \({PO={3\over 4}{R}}\) oraz \({UP=PO-UO={3\over 4}{R}-3r}.\)
Oznaczając \({\varphi=\measuredangle{PAO}=\measuredangle{PUX}},\) mamy \({R\,{\rm{tg}\,}\varphi=OA\,{\rm{tg}\,}\varphi=OP={3\over 4}{R}},\) więc \({{\rm{tg}\,}\varphi={3\over 4}},\) wobec czego \({\cos\varphi={4\over 5}},\) \({\sin\varphi={3\over 5}}.\) Dalej, \({3r=UX=UP\cos\varphi=({3\over 4}{R}{-}3r){\cdot}{4\over 5}},\) skąd \({R=9r}.\) I ostatecznie: \({d=AC=AB\cos\varphi=2R\cdot{4\over 5}=18r\cdot{4\over 5}}.\)
Mamy odpowiedź na pytanie z zadania: \({r/{d}=5/72}.\)
902. Liczba \(w(n)\) to także największy wykładnik, dla którego \(n!\) dzieli się przez \(5^{w(n)}\) (bo w rozkładzie \(n!\) jest więcej dwójek niż piątek); w standardowych symbolach: \({w(n)=v_5(n!)}.\)
Ustalmy \({m\in{\mathbb N}}.\) Określamy rozłączne zbiory \(A_0,A_1,\ldots,A_m,\) zawarte w \(\{1,2,\ldots,5^m\}\): \[A_j=\{k\cdot5^j\colon\;1\le{k}\le5^{m-j};\;\;k\perp5\}\ \ \ \ \hbox{dla}\ j=0,1,\ldots,m. \tag{1}\] Dla \({j<m}\) liczność zbioru \(A_j\) wynosi tyle, ile jest liczb \({k\le5^{m-1}}\) niepodzielnych przez 5; czyli \[|A_j|=4\cdot5^{m-j-1}\ \ \ \ \hbox{dla}\ j<m. \tag{2}\]Łączna liczność zbiorów \(A_0,\ldots,A_{m-1}\) z dołączonym zbiorem jednoelementowym \({A_m=\{1\cdot5^m\}}\) wynosi \({4\sum_{j=0}^{m-1}5^{m-j-1}+1=5^m}.\) Ich elementy nie przekraczają \(5^m,\) więc tworzą permutację zbioru \(\{1,\ldots,5^m\}\); skąd wniosek, że iloczyn wszystkich tych elementów wynosi \((5^m)!.\)
Zapiszmy iloczyn elementów zbioru \(A_j\) jako \(5^{\alpha_j}P_j,\) gdzie \({P_j\perp5}.\) Wymnażając (po \({j=0,\ldots,m}\)), dostajemy \[(5^m)!=5^{\alpha_0+\ldots+\alpha_m}Q,\ \ \ \hbox{gdzie}\ Q=P_0\ldots P_{m-1}P_m\perp5. \tag{3}\] Oczywiście \({\alpha_m=m},\) \({P_m=1}\); zaś dla \({j<m}\) mamy, zgodnie z określeniem (1), \({\prod_{a\in{A_j}}{\!\!}a=\bigl((5^j)^{|A_j|}\bigr)P_j},\) więc \({\alpha_j=j\cdot|A_j|}.\) To liczba podzielna przez 4 (wzór (2)). Ponadto \[P_j=\prod_{k\le5^{m-j},\,k\perp5}{\!\!\!}k =(1{\cdot}2{\cdot}3{\cdot}4)\cdot (6{\cdot}7{\cdot}8{\cdot}9)\cdot \ldots\cdot({\cdots})\ \ \ \hbox{dla}\ j<m.\] W tym ostatnim przedstawieniu mamy \({{1\over 4}|A_j|}\) czynników \((\,)(\,)\ldots(\,),\) a to liczba nieparzysta (wzór (2)). Dlatego \({P_j\equiv4}\) (mod 5); a stąd, zgodnie z (3), \({Q\equiv4^m}\) (mod 5).
Równość (3) pokazuje, że \({w(5^m)=\alpha_0+\ldots+\alpha_m=4l+m}\) dla pewnego \(l\) (bo \(4{\mid}\alpha_j\) dla \({j<m}\)). Zatem \[\begin{aligned} f(5^m) & =10^{-w(5^m)}(5^m)!=10^{-w(5^m)}{\cdot}5^{w(5^m)}Q=2^{-w(5^m)}Q \\&=2^{-4l-m}Q, \end{aligned}\] skąd ostatecznie \({f(5^m)\equiv2^{-4l}\cdot2^{-m}\cdot4^m\equiv2^m}\) (mod 5); to teza zadania.
Zadania z fizyki nr 802, 803
Termin nadsyłania rozwiązań: 30 XI 2025
Redaguje Elżbieta ZAWISTOWSKA
802. Podróżny stał obok początku wagonu z numerem porządkowym \(k.\) Pociąg ruszył z miejsca, po czym okazało się, że wagon o numerze \(m\) mijał pasażera przez \(t\) sekund. Ile czasu przejeżdżał obok tego pasażera wagon o numerze \(n\)? Pociąg poruszał się ruchem jednostajnie przyspieszonym, długości wagonów są jednakowe, odległości między wagonami zaniedbywalne. Podróżny nie poruszał się względem peronu.
803. Dwie metalowe kule o promieniach \(R\) znajdują się w bardzo dużej odległości od siebie i połączone są cienkim przewodnikiem, w którego rozcięcie włączona jest cewka o współczynniku samoindukcji \(L.\) W chwili początkowej jedna z tych kul naładowana jest ładunkiem \(Q,\) druga nienaładowana. Po jakim czasie ładunek kuli naładowanej zmaleje dwukrotnie?
Errata: W wersji drukowanej pytanie z zadania 803 było błędnie odniesione do kuli nienaładowanej
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
792 (\(WT=3{,}23\)), 793 (\(WT=2{,}07\))
z numeru 2/2025
Jacek Konieczny Poznań 41,11 Jan Zambrzycki Białystok 4 – 34,42 Andrzej Nowogrodzki Chocianów 3 – 29,48 Paweł Kubit Kraków 17,21 Paweł Perkowski Ożarów Maz. 6 – 15,13 Tomasz Wietecha Tarnów 18 – 13,15 Krzysztof Zygan Lubin 13,02
Rys. 1
Rys. 2
Rys. 3
Rozwiązania zadań z numeru 5/2025
Przypominamy treść zadań:
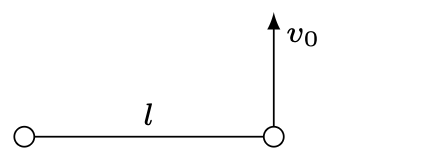
798. Dwie bardzo małe jednakowe kulki związane nieważką, nierozciągliwą nicią leżą na powierzchni poziomej (rys. 1).
Jednej z kulek nadano prędkość \(v_{0}\) skierowaną pionowo w górę. Jaka powinna być wartość tej prędkości, aby druga kulka nie oderwała się od poziomej powierzchni, a nić przez cały czas była naciągnięta? Po jakim torze porusza się wtedy pierwsza kulka? Tarcie kulki o podłoże jest zaniedbywalne.799. Elektron krąży po orbicie kołowej w jednorodnym polu magnetycznym. Indukcja pola magnetycznego zostaje powoli zwiększona trzy razy, w czasie wielokrotnie przewyższającym okres obrotu. Ile razy zmieni się w tym czasie promień orbity elektronu?
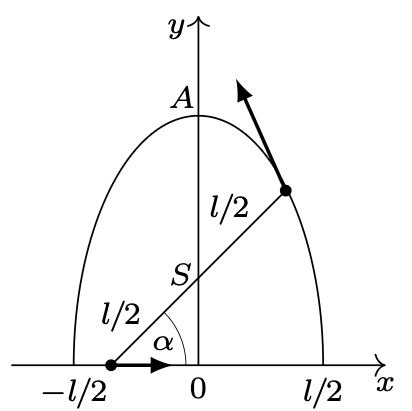
798. Ponieważ nie ma tarcia, a prędkość nadana jednej z kulek jest pionowa, środek masy układu porusza się w kierunku pionowym. Obie kulki uczestniczą w ruchu złożonym – ruch po okręgu o promieniu \({l\over 2}\) wokół środka nici nakłada się na ruch tego środka wzdłuż linii pionowej. Wybierzmy układ współrzędnych jak na rysunku 2. Dolna
kulka porusza się wzdłuż osi \(x\), jej prędkość w każdej chwili jest równa co do wartości składowej poziomej prędkości górnej kulki i przeciwnie skierowana. Współrzędne \(x\) i \(y\ \)górnej kulki możemy wyrazić przez kąt \(\alpha\): \[x = {l\cos\alpha\over 2},\ \ \ y = l\sin\alpha.\] Eliminując \(\alpha\) z równań (1), otrzymujemy równanie elipsy o półosiach \({l\over 2}\) i \(l\): \[{x^{2}\over\left( {l\over 2} \right)^{2}} + {y^{2}\over l^{2}} = 1.\]Gdy górna kulka wznosi się, jej prędkość maleje. Siła ciężkości odgrywa coraz większą rolę w zakrzywianiu jej toru, co powoduje zmniejszanie siły napięcia nici. Aby znaleźć najmniejsze napięcie, musimy rozważyć sytuację w najwyższym punkcie toru.
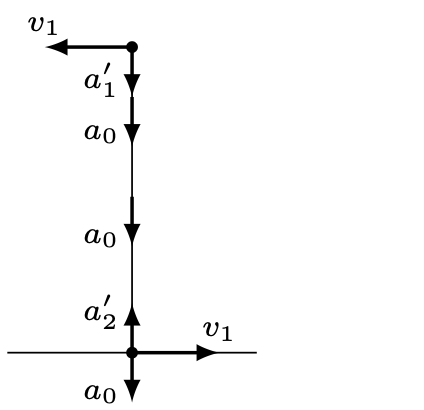
Zasada zachowania energii pozwala obliczyć wartość prędkości \(v_{1}\) w punkcie \(A,\) jednakową dla obu kulek: \[{mv_{0}^{2}\over 2} = 2{mv_{1}^{2}\over 2} + mgl,\text{ stąd } v_{1}^{2} = {v_{0}^{2}\over 2} - gl.\] Oznaczmy przyspieszenie środka masy układu w chwili, gdy górna kulka znajduje się w punkcie \(A\) przez \(a_{0}\), przyspieszenia dośrodkowe kulek przez \(a_{1}'\) i \(a_{2}'\) (rys. 3), a ich
przyspieszenia całkowite przez \(a_{1}\) i \(a_{2}\). Spełnione są równania: \[\begin{aligned} {a_{1}}' & = a_{2}' = {v_{1}^{2}\over\left( {l\over 2} \right)}, \\ a_{2} & = a_{2}' - a_{0} = 0,\text{ stąd } a_{0} = {2v_{1}^{2}\over l}, \\ a_{1} & = a_{1}' + a_{0} = {4v_{1}^{2}\over l}. \end{aligned}\] Minimalne napięcie nici \(N\) znajdziemy z równania ruchu górnej kulki oraz równania (2): \[N + mg = {4mv_{1}^{2}\over l} \implies N={2mv_{0}^{2}\over l} - 5mg.\] Nić będzie cały czas napięta podczas ruchu, gdy \(N > 0\), stąd \(v_{0}^{2} > {5gl\over 2}\).Dolna kulka nie oderwie się od podłoża, gdy \(N < mg\), stąd \(v_{0}^{2} < 3gl\).
Górna kulka zakreśli połowę elipsy i uderzy o podłoże. Jeśli zderzenie będzie sprężyste, to zakreśli ten sam tor w przeciwnym kierunku.
799. Siła Lorentza nadaje elektronowi przyspieszenie dośrodkowe. Zgodnie z drugą zasadą dynamiki \[{mv^{2}\over R} = evB,\] gdzie \(m\) jest masą, a \(e\) wartością bezwzględną ładunku elektronu. Zmiana pola magnetycznego powoduje pojawienie się wirowego pola elektrycznego \(E\). Zgodnie z prawem Maxwella natężenie \(E\) tego pola dla krótkiego czasu \(\Delta t\) spełnia równanie \[% 2\pi RE = {\Delta \Phi_{B}\over\Delta t} = {\pi R^{2}\Delta B\over\Delta t},\] stąd \[E = {R\Delta B\over(2\Delta t)}.\] Siła elektryczna przyspiesza elektron, zmienia się jego prędkość i promień orbity, ale zależność (1) nadal jest spełniona.
Praca siły elektrycznej w krótkim czasie \(\Delta t\) zmienia energię kinetyczną elektronu: \[\begin{aligned} \notag & eEv\Delta t = \Delta \left( {mv^{2}\over 2} \right) \approx mv\Delta v, \\ & \Delta v \approx {eR\Delta B\over(2m)}. \end{aligned}\] Z drugiej strony, z równania (1), mamy: \[\Delta v \approx {e(R\Delta B + B\Delta R)\over m}.\] Z porównania (3) i (4): \[\Delta(BR^2)=R^2\Delta B+2BR\Delta R=R(R\Delta B+ 2B\Delta R)=0.\] Oznacza to, że przy zmianie pola magnetycznego wielkość \(BR^{2}\) zachowuje się. Trzykrotny wzrost pola magnetycznego powoduje, że promień orbity maleje \(\sqrt{3}\) razy.