Zadania z matematyki nr 907, 908
Termin nadsyłania rozwiązań: 31 XII 2025
Redaguje Marcin E. KUCZMA
907. Niech \(n\) będzie ustaloną liczbą naturalną, \({n\ge3}.\) Znaleźć największą liczbę naturalną \(m,\) dla której istnieją różne liczby rzeczywiste \(x_1,\ldots,x_m\) takie, że wartość wyrażenia \[\sum_{i=0}^n x_k^{n-i}x_l^i\] jest jednakowa dla każdej pary różnych numerów \({k,l\in\{1,\ldots,m\}}.\)
908. Wyznaczyć wszystkie liczby całkowite \({a\ge1}\) o tej własności, że dla każdej liczby całkowitej \({n\ge1}\) suma \({1+a+\ldots+a^{n-1}}\) jest liczbą trójkątną.
Zadanie 908 zaproponował pan Witold Bednarek z Łodzi.
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
897 (\(WT = 2{,}97\)) i 898 (\(WT = 1{,}22\))
z numeru 3/2025
Marek Spychała Warszawa 47,41 Piotr Wiśniewski Warszawa 45,51 Grzegorz Wiączkowski 44,90 Marcin Kasperski Warszawa 43,44 Andrzej Daniluk Warszawa 40,76 Krzysztof Kamiński Pabianice 38,09 Krzysztof Maziarz Londyn 38,05 Jerzy Cisło Wrocław 37,59 Marian Łupieżowiec Gliwice 35,90 Barbara Mroczek 34,09 Mikołaj Znamierowski 33,62 Roksana Słowik 33,00 Pan Marek Spychała to już dwukrotny Weteran: \({6\times 44}\)(!). Pan Piotr Wiśniewski goni czołówkę: \({2\times 44},\) w krótkim czasie. A pan Grzegorz Wiączkowski, \({1\times 44},\) to nowa postać w naszym Klubie – w ostatnich czasach nie tak często mamy okazję witać nowych przybyszów.
Rozwiązania zadań z numeru 6/2025
Przypominamy treść zadań:
903. Funkcje \(f\) i \(g\) są dane wzorami \[\begin{aligned} f(x) & =(1+x+x^2+x^3+\ldots+x^{42})+45x^{43}, \\ g(x) & =(1+x+x^2+x^3+\;\;\ldots\;\;+x^{44})+45x^{45}. \end{aligned}\] Liczby rzeczywiste \(a,b\) spełniają warunki \({f(a)=g(b)=44}.\) Wyjaśnić, która z liczb \(a,b\) jest większa.
904. Niech \({A_1=31},\) \({A_2=331},\) …, \({A_n=33\ldots31}\) (\(n\) trójek, a na końcu jedynka – zapis dziesiętny). Dla każdej liczby pierwszej \({p<44}\) rozstrzygnąć, czy istnieje liczba \(n\) (zależna od \(p\)), dla której \(A_n\) dzieli się przez \(p.\) Jeśli istnieje, ustalić, czy jest wówczas nieskończenie wiele, czy tylko skończenie wiele takich numerów \(n.\)
903. Z równości \[% \begin{aligned} (x-1)f(x) & =x^{43}-1+45(x^{44}-x^{43}) \\&=45x^{44}-44x^{43}-1,\\ (x-1)g(x) & =x^{45}-1+45(x^{46}-x^{45}) \\&=45x^{46}-44x^{45}-1 \end{aligned} \tag{1}\] otrzymujemy związek \[(x-1)(g(x)-f(x))=x^{43}(x^2-1)(45x-44),\] i dalej (dla \({x\ne1},\) ale dla \({x=1}\) też, bo to wielomiany): \[g(x)-f(x)=x^{43}(x+1)(45x-44). \tag{2}\] Liczby \(a,b\) dane są równaniem \({f(a)=g(b)=44}.\) Dla \({x<0}\) mamy na mocy wzorów (1): \[\begin{aligned} (x-1)(f(x)-44) & =45x^{44}-44x^{43}-1-44x+44>0, \\ (x-1)(g(x)-44) & =45x^{46}-44x^{45}-1-44x+44>0, \end{aligned}\] więc \({f(x)-44<0},\) \({g(x)-44<0}\) (dla \({x<0}\)). Zatem \({a,b\ge0}.\)
Ze wzoru (2) widać, że \({f\bigl({44\over 45}\bigr)=g\bigl({44\over 45}\bigr)}.\) Prosty rachunek (oparty na wzorach (1)) pokazuje, że ta wspólna wartość wynosi 45. W zbiorze liczb nieujemnych funkcje \(f,g\) są ściśle rosnące, przy czym \({f(0)=g(0)=1}.\) Stąd wniosek, że \({a,b\in\bigl(0,{44\over 45}\bigr)}.\) Ponieważ \({f(x)>g(x)}\) w tym przedziale (wzór (2)), więc gdyby zachodziła nierowność \({a\ge{b}},\) mielibyśmy \({44=f(a)>g(a)\ge g(b)=44},\) sprzeczność. Stąd odpowiedź na pytanie zadania: \({a<b}.\)
904. Liczba \(A_n\) wyraża się wzorem \[A_n=\textstyle{1\over 3}(10^{n+1}-1)-2={1\over 3}(10^{n+1}-7).\] Widać od razu, że (dla żadnego \(n\)) nie dzieli się przez \(2,3,5,7.\) Dalej badamy podzielność przez liczby pierwsze \({p\in[11,43]}.\) Jest to więc pytanie o to, czy w ciągu \(10,100,1000,\ldots\) (mod \(p\)) pojawia się siódemka. Jeżeli tak – niech np. \({10^m\equiv7}\) (mod \(p\)) – to ponieważ \({10^{p-1}\equiv1}\) (mod \(p\)), więc minimalny taki wykładnik \(m\) znajduje się w przedziale \([0,p{-}2].\) Dla każdego \({k\ge0}\) mamy wówczas \({10^{k(p-1)+m}\equiv7}\) (mod \(p\)), co oznacza, że w tym przypadku istnieje nieskończenie wiele liczb \(n,\) o jakie pyta zadanie. Jeżeli natomiast wśród liczb \(10,10^2,\ldots,10^{p-2}\) branych (mod \(p\)) nie ma siódemki, to nie ma jej w całym nieskończonym ciągu \(10,10^2,10^3,\ldots\) (mod \(p\)), więc nie istnieje liczba \(n,\) o jaką pyta zadanie.
Rozstrzygnięcie (dla \({p<44}\)) kwestii; siódemka [pojawia się/nie pojawia się] najprościej uzyskać, pisząc banalny programik numeryczny. Wychodzi odpowiedź tak dla \({p=17,19,23,29,31}\) (minimalny wykładnik \(m\) wynosi, odpowiednio, \(9,12,21,20,2\)); nie dla \({p=2,3,5,7,11,13,37,41,43}.\)
[Czytelników, którzy z niechęcią widzą użycie urządzenia obliczeniowego, zachęcamy do ręcznego przeszukania stosownych wartości (zamiast badania potęg \(10^l\) dla \({l<p{-}1}\) wystarczy rozważać \({l<\delta},\) gdzie \({\delta=\min}\): \({10^\delta\equiv1}\) (mod \(p\))). Stosując proste sztuczki w operowaniu kongruencjami, daje się to zrobić w przeciągu kilkunastu minut na niewielkiej kartce papieru.]
Zadania z fizyki nr 804, 805
Termin nadsyłania rozwiązań: 31 XII 2025
Redaguje Elżbieta ZAWISTOWSKA
804. Chłopiec znajduje się w punkcie \(A\) na brzegu rzeki, której prędkość nurtu wynosi \(w\) (rys. 1). Chłopiec może biec po brzegu z prędkością \(v\) i płynąć rzeką z prędkością \(u\) względem wody, przy czym \(u<v.\) W jakiej odległości od punktu \(A\) znajduje się na brzegu punkt \(C,\) z którego chłopiec powinien zacząć płynąć, aby dotrzeć do punktu \(B\) w najkrótszym czasie? Odległość \(|BD|\) punktu \(B\) od brzegu wynosi \(h,\) odległość \(|AD|\) jest równa \(l.\)
Rys. 1
Rys. 2
Rys. 3
805. Para jednakowych małych kulek \(A\) i \(B\) połączonych nieważką nicią o długości \(l\) zaczyna ześlizgiwać się z gładkiego stołu o wysokości \(l,\) przy czym w chwili początkowej kulka \(B\) znajduje się na wysokości \(h=2l/3\) nad podłogą (rys. 2). Po dotknięciu podłogi kulka \(B\) przykleja się do niej, a kulka \(A\) spada w tym momencie ze stołu. Od jakiej wysokości kulki \(A\) nad podłogą nić będzie napięta?
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
794 (\(WT=3{,}7\)), 795 (\(WT=2{,}5\))
z numeru 3/2025
Jacek Konieczny Poznań 41,11 Jan Zambrzycki Białystok 4 – 35,42 Andrzej Nowogrodzki Chocianów 3 – 29,98 Paweł Perkowski Ożarów Maz. 6 – 17,63 Paweł Kubit Kraków 17,21 Tomasz Wietecha Tarnów 18 – 14,63 Krzysztof Zygan Lubin 14,52
Rozwiązania zadań z numeru 6/2025
Przypominamy treść zadań:
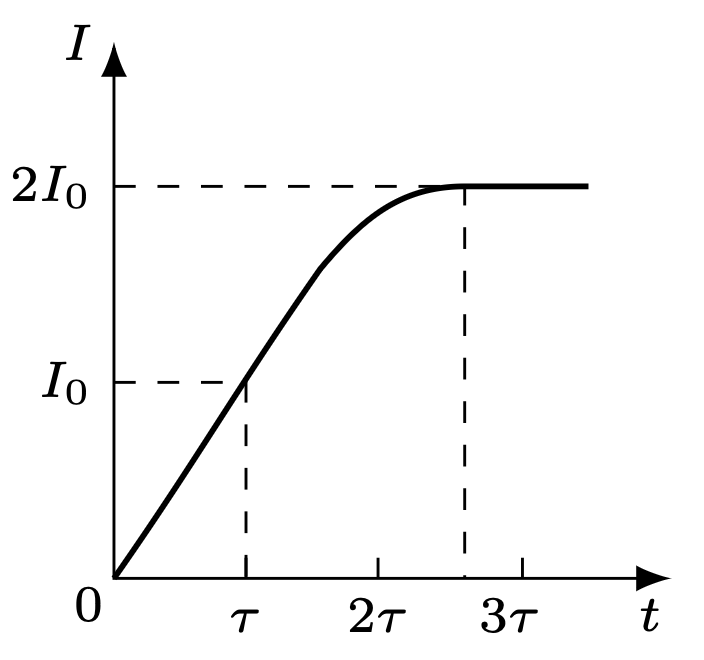
800. W obwodzie przedstawionym na rysunku 3 dioda jest idealna i wszystkie opory omowe zaniedbywalne. Klucz \(K\) zamknięto na czas \(\tau,\) a następnie otwarto. W chwili otwierania klucza natężenie prądu w cewce miało wartość \(I_{0}.\) Po jakim czasie po otwarciu klucza osiągnęło ono wartość maksymalną równą \(2I_{0}\)? Narysuj wykres zależności natężenia prądu w cewce od czasu \(t\) \((0<t<\infty)\).
801. Statek kosmiczny przemieszcza się od Ziemi do Marsa po orbicie eliptycznej, której peryhelium znajduje się na orbicie Ziemi, a aphelium na orbicie Marsa. Znaleźć czas przelotu oraz minimalny czas, w jakim kosmonauci będą musieli oczekiwać na Marsie na start w drogę powrotną po takiej samej orbicie. Okres obiegu Ziemi wokół Słońca wynosi \(T_{\rm Z}=365{,}25\) dób, okres obiegu Marsa \(T_{\rm M}=687\) dób. Przyjąć, że planety poruszają się po orbitach kołowych leżących w jednej płaszczyźnie.
800. Po zamknięciu klucza \(K\) napięcie na kondensatorze i cewce w bardzo krótkim czasie osiąga wartość \(\varepsilon\) równą sile elektromotorycznej źródła. W przedziale czasowym \(\tau\) ładunek na kondensatorze o pojemności \(C\) ma stałą wartość \(C\varepsilon\) (prąd przez diodę nie płynie), a prąd płynący przez cewkę o współczynniku samoindukcji \(L\) narasta liniowo: \[L{dI\over dt} = \varepsilon\ \Rightarrow \ I = {\varepsilon t\over L},\ \ \ 0 < t \leq \tau.\] W chwili \(t = \tau\), zgodnie z treścią zadania: \[I(\tau) = I_{0} = \varepsilon\tau/L.\] Po otwarciu klucza natężenie prądu w cewce nadal rośnie w wyniku rozładowywania kondensatora. \[{Q\over C} + L{dI\over dt} = 0,\ \ \ I = {dQ\over dt},\ \ \ {d^{2}I\over dt^{2}} + {I\over(LC)} = 0,\ \ \ Q(\tau) = C\varepsilon.\] Ładunek na kondensatorze nie może zmienić się skokowo, zatem prostoliniowy odcinek zależności natężenia prądu w cewce od czasu przechodzi płynnie (bez skoku pochodnej) na część sinusoidy, której okres \(T = 2\pi/\omega = 2\pi\sqrt{LC}\) (rys. 4).
Z zasady zachowania energii \[{L{I_{0}}^{2}\over 2} + {C\varepsilon^{2}\over 2} = {L{I_{\max}}^{2}\over 2},\ \ \ \text{gdzie \(I_{\max} = 2I_{0} = {2\varepsilon\tau\over L}\),}\] otrzymujemy: \[LC = 3\tau^{2}.\] Natężenie prądu w cewce zmienia się od wartości \(I_{0}\) do \(2I_{0}\), gdy wartość sinusa zmienia się od \({1\over 2}\) do 1, a jego argument od \(\pi/6\) do \(\pi/2\), czyli szukany czas wynosi: \[{\Delta\tau} = T/6 = \pi\sqrt{3}\tau/3 \cong 1{,}8\tau.\] W chwili \(t = \tau + {\Delta}\tau \cong 2{,}8\tau\) potencjały punktów \(A\) i \(B\) wyrównują się, opór odcinka z diodą w kierunku od \(B\) do \(A\) staje się równy zeru. Od tego momentu przez cewkę płynie stały prąd \(2I_{0}\), a ładunek kondensatora wynosi 0.
 Rys. 4
Rys. 4
 Rys. 5
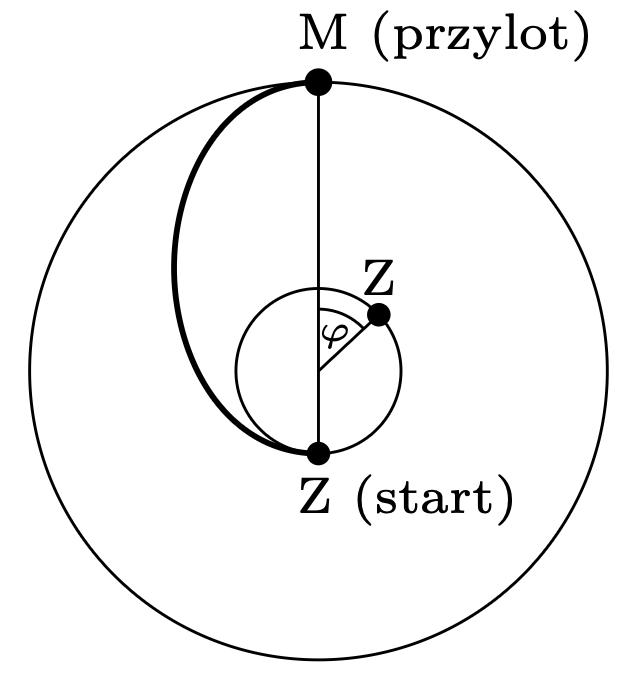
Rys. 5
801. Półoś wielka \(a\) orbity, po której porusza się statek kosmiczny, równa jest połowie sumy promieni orbit Ziemi i Marsa (rys. 5): \(a = {\left( a_{\rm Z} + a_{\rm M} \right)\over 2}.\) Zgodnie z trzecim prawem Keplera \(a_{\rm Z}\sim{T_{\rm Z}}^{2/3}\) i \(a_{\rm M}\sim{T_{\rm M}}^{2/3}\). Analogicznie związana jest półoś wielka orbity statku i okres jego obiegu \(T\): \(a\sim T^{2/3}\). Stąd \(T^{2/3} = {( {T_{\rm Z}}^{2/3} + {T_{\rm M}}^{2/3} )\over 2}.\) Szukany czas przelotu statku od Ziemi do Marsa jest równy \[\tau = {( {T_{\rm Z}}^{2/3} + {T_{\rm M}}^{2/3})^{3/2}\over 2^{5/2}} \cong 259\text{ dób.}\] W chwili przylotu Ziemia wyprzedza Marsa o kąt \[\varphi = \omega_{\rm Z}\tau - \pi = {2\pi\tau\over T_{\rm Z} - \pi},\] gdzie \(\omega_{\rm Z}\) jest prędkością kątową ruchu Ziemi względem Słońca. W chwili startu w podróż powrotną Ziemia powinna być cofnięta względem Marsa o taki sam kąt \(\varphi\), innymi słowy – powinna wyprzedzać go o kąt \(2\pi - \varphi\ \)(czas oczekiwania na Marsie ma być minimalny). Czas, po którym kąt wyprzedzenia zmienia się od \(\varphi\ do\ 2\pi - \varphi\), wynosi \[t = {(2\pi - 2\varphi)\over\left( \omega_{\rm Z} - \omega_{\rm M} \right)},\] gdzie \(\left( \omega_{\rm Z} - \omega_{\rm M} \right)\) jest względną prędkością kątową ruchu Ziemi i Marsa. Minimalny czas oczekiwania kosmonautów na Marsie jest równy \[t = {( 2 - 2{\tau\over T_{\rm Z}} )\over( {1\over T_{\rm Z}} - {1\over T_{\rm M}} ) \cong 457}\text{ dób.}\]