Turniej Młodych Fizyków to konkurs drużynowy dla uczniów szkół średnich, który łączy badania naukowe z prezentacją ich wyników w formie publicznej debaty.
Uczestnicy mają niemal cały rok na zmierzenie się z 17 otwartymi problemami fizycznymi – wymagającymi zarówno kreatywności, jak i solidnej wiedzy teoretycznej.
Praca nad zagadnieniami obejmuje projektowanie i przeprowadzanie doświadczeń, formułowanie modeli teoretycznych, stawianie hipotez oraz ich weryfikację.
Uczniowie mogą korzystać z literatury, internetu oraz pomocy nauczycieli i naukowców.
Efektem tych przygotowań są prezentacje, które uczestnicy przedstawiają na scenie podczas zawodów – a następnie bronią swoich tez w dyskusji z przeciwnikiem i recenzentem. Aby wziąć udział w turnieju, wystarczy stworzyć pięcioosobowy zespół licealistów oraz znaleźć nauczyciela-opiekuna.
Do 18 stycznia 2026 r. należy przesłać rozwiązania dziesięciu z siedemnastu problemów.
Najlepsze zespoły zostaną zaproszone do udziału w półfinałach, które odbędą się w marcu i przyjmą formę tzw. potyczek fizycznych.
Finał ogólnopolski, zaplanowany na kwiecień, wyłoni reprezentację Polski na Międzynarodowy Turniej Młodych Fizyków, który w 2026 roku odbędzie się w Szwajcarii.
Szczegóły oraz listę zagadnień można znaleźć na stronie: tmf.org.pl.
Zagadnienia Turnieju Młodych Fizyków 2026
1. Wymyśl sam. Sztywną rurkę wygiętą w odpowiedni kształt można wykorzystać do zbudowania syfonu, który po częściowym zanurzeniu w wodzie sam zaczyna zasysać ciecz, bez potrzeby wstępnego odsysania powietrza. Zbadaj, w jaki sposób istotne parametry, takie jak geometria rurki, wpływają na działanie syfonu.
2. Tłumienie elektryczne. Magnes zawieszony na sprężynie, po wychyleniu z punktu równowagi, wykonuje drgania harmoniczne. Jeżeli magnes oscyluje wewnątrz solenoidu połączonego z rezystorem, ruch jest tłumiony. Zbadaj czynniki wpływające na tłumienie.
3. Pierścieniowa fontanna. Płaski metalowy pierścień, spadając z pewnej wysokości do zbiornika z wodą, powoduje powstanie fontanny, która może wyrzucać wodę na znaczną wysokość. Jak parametry pierścienia wpływają na maksymalną wysokość osiąganą przez wodę?
4. Rozlewający się olej. Cienka warstwa oleju spożywczego na płaskiej metalowej powierzchni rozpływa się na zewnątrz, gdy powierzchnia zostanie podgrzana. Zbadaj to zjawisko i jego zależność od odpowiednich parametrów.
5. Dynamika fal sprężystych. Zawieś metalową kulkę na gumce recepturce przymocowanej do nieruchomego uchwytu i skręć ją wielokrotnie wokół osi pionowej. Po zwolnieniu kulki w gumce powstają fale stojące. Zbadaj zjawisko i określ, jak powstająca fala zależy od istotnych parametrów.
6. Flipo Flip. Zabawka Flipo Flip potrafi toczyć się, wykonując wiele obrotów, mimo że jej kształt nie jest kolisty. Zbadaj, jak parametry takie jak geometria zabawki oraz warunki początkowe wpływają na jej ruch.
7. Twierdzenie o rakiecie tenisowej. Bryła o różnych momentach bezwładności względem swoich osi głównych, rzucona z nadanym obrotem, może nagle zmienić oś obrotu na inną niż początkowa. Zbadaj, jak podczas swobodnego spadku ruch obrotowy takiego ciała zależy od istotnych parametrów.
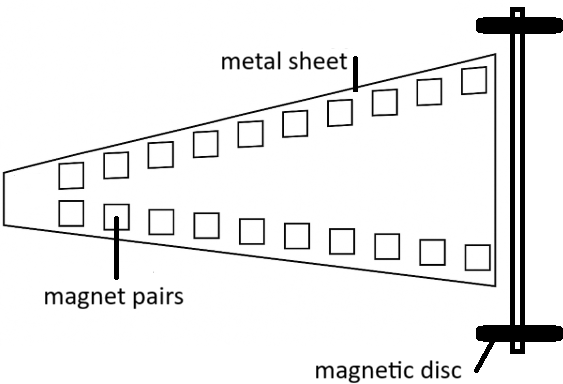
8. Magnetyczny akcelerator. Przytwierdź pary magnesów do metalowej płyty, jak w układzie przedstawionym na rysunku. Jeśli na osi osadzisz dwa magnetyczne dyski, ten „pojazd” może, w pewnych warunkach, przyspieszać wzdłuż rzędów magnesów. Zbadaj to zjawisko.
9. Sterowanie lewitacją. Odpowiednio ułożone cienkie płytki grafitu mogą lewitować nad magnesami neodymowymi. Oświetlając powierzchnię grafitu, można sterować jego ruchem. Zbadaj i wyjaśnij to zjawisko.
10. Zanurzony krater. Jeśli wsypiesz piasek lub podobny materiał ziarnisty do pojemnika wypełnionego wodą, ziarna opadną na dno i mogą utworzyć strukturę przypominającą krater. Zbadaj i wyjaśnij to zjawisko.
11. Słodki monochromator. Przepuść liniowo spolaryzowane światło białe przez kolumnę roztworu cukru. Przy obserwacji światła za pomocą polaryzatora mogą pojawić się kolory. Obracając polaryzator, można zmieniać obserwowany kolor. Zbuduj taki „słodki monochromator” i zoptymalizuj układ, aby uzyskać możliwie najwęższe pasmo długości fali.
12. Jesienna moneta. Ruch monety opadającej na dno zbiornika z cieczą może przypominać trzepotanie i koziołkowanie opadającego jesiennego liścia. Zbadaj, jak ruch monety zależy od istotnych parametrów.
13. Śpiewająca linijka. Linijka, z unieruchomionym jednym końcem, po uderzeniu drga i wydaje charakterystyczny dźwięk. Zbadaj, jak dźwięk zależy od istotnych parametrów.
14. Krystaliczne stworki. Zaobserwuj parowanie kropli roztworu soli kuchennej na podgrzanej hydrofobowej powierzchni. Po odparowaniu wody pozostają różnorodne, charakterystyczne kształty kryształów. Zbadaj i wyjaśnij to zjawisko.
15. Magnetyczna kołyska Newtona. Nowy rodzaj kołyski Newtona może zostać skonstruowany z użyciem odpychających, niestykających się magnesów, zamiast zderzających się kulek. Taka kołyska potrafi zachowywać się podobnie do zwykłej, a jednocześnie wykazuje też inne interesujące efekty. Zbadaj i wyjaśnij ruch tej magnetycznej kołyski.
16. Skręcone spaghetti. Skręcony pęczek spaghetti może wytrzymać większe siły poprzeczne niż prosty, nieskręcony pęczek. Zbadaj, jak skręcony pęczek spaghetti reaguje na poprzeczne obciążenie i wyznacz optymalny kąt skręcenia maksymalizujący wytrzymałość.
17. Wędrujący płomień. Płomień może nieprzerwanie wędrować po pierścieniowym rowku wypełnionym cienką warstwą łatwopalnej cieczy. Zbadaj, od jakich parametrów zależą właściwości tego wędrującego płomienia.
