Afiliacja: Katedra Matematyki i Informatyki, Uniwersytet Jana Długosza w Częstochowie
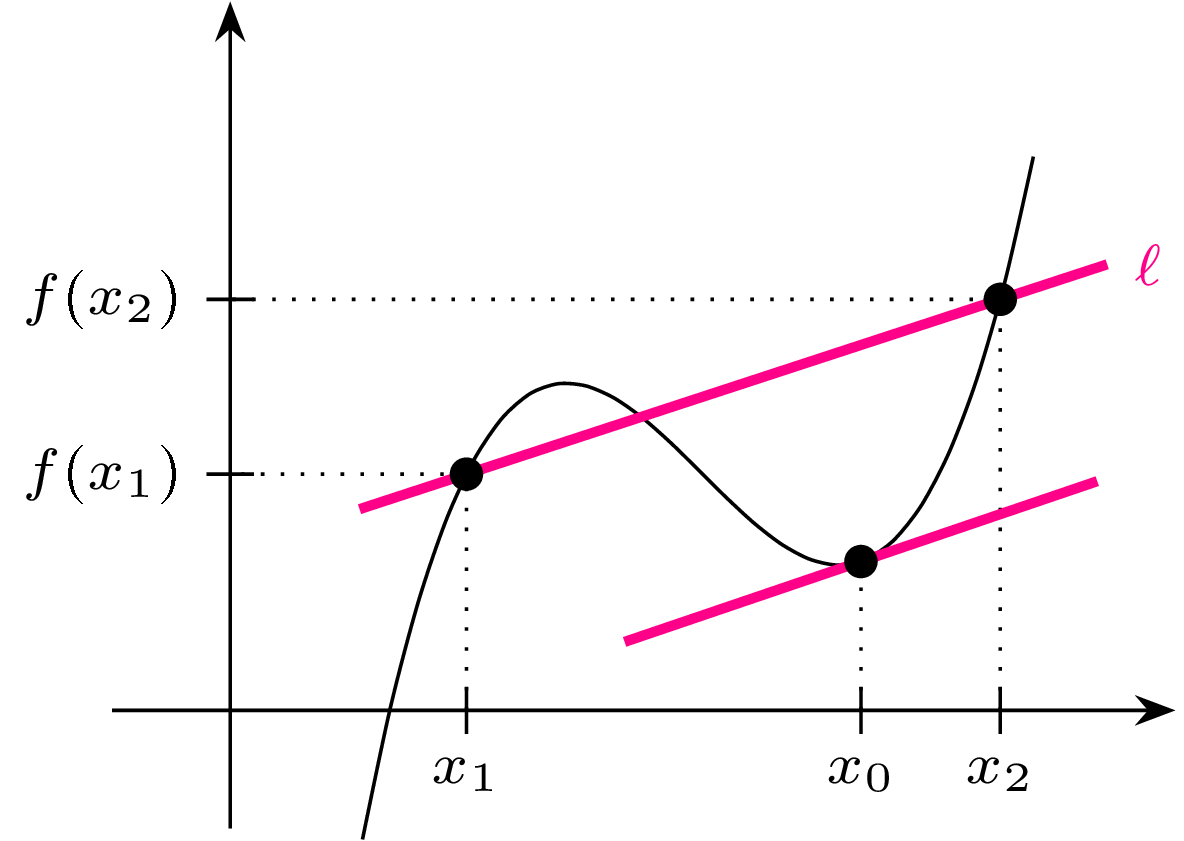
Czy dla każdej siecznej do wykresu da się znaleźć równoległą do niej styczną? Lub bardziej precyzyjnie, czy mając daną funkcję \(f\) i sieczną \(\ell\) poprowadzoną przez punkty o odciętych \(x_1 < x_2,\) można tak dobrać punkt \(x_0 \in (x_1,x_2),\) żeby styczna do wykresu funkcji \(f\) w \((x_0,f(x_0))\) była równoległa do \(\ell\)?
Sieczną \(\ell,\) o której tu mowa, jest prosta nachylona do osi \(Ox\) układu współrzędnych pod kątem, którego tangens – jak łatwo dostrzec – jest równy ilorazowi \(\frac{f(x_2)-f(x_1)}{x_2-x_1}.\) Tangens kąta nachylenia stycznej w \((x_0,f(x_0))\) jest zadany przez pochodną: \(f'(x_0).\) Pytanie o prostą styczną równoległą do \(\ell\) jest więc pytaniem o istnienie \(x_0 \in (x_1,x_2)\) o własności \[f'(x_{0}) = \frac{f(x_2)-f(x_1)}{x_2-x_1}.\] Jak powszechnie wiadomo, odpowiedź na powyższe pytanie (dla funkcji \(f\) różniczkowalnej w danym przedziale) przynosi klasyczne twierdzenie Lagrange’a o wartości średniej. Odpowiedź jest pozytywna. Trzeba tylko nadmienić, że szukana styczna nie musi być jedyna, a teza twierdzenia nie daje nam jawnego wzoru na punkt \(x_0,\) którego istnienie jest ową tezą zapewnione.
Rys. 1. Sieczna \(\ell\) poprowadzona przez punkty \((x_1,f(x_1))\) i \((x_2,f(x_2))\) oraz poprowadzona przez \((x_0,f(x_0))\) styczna równoległa do \(\ell\) (nie jedyna!)
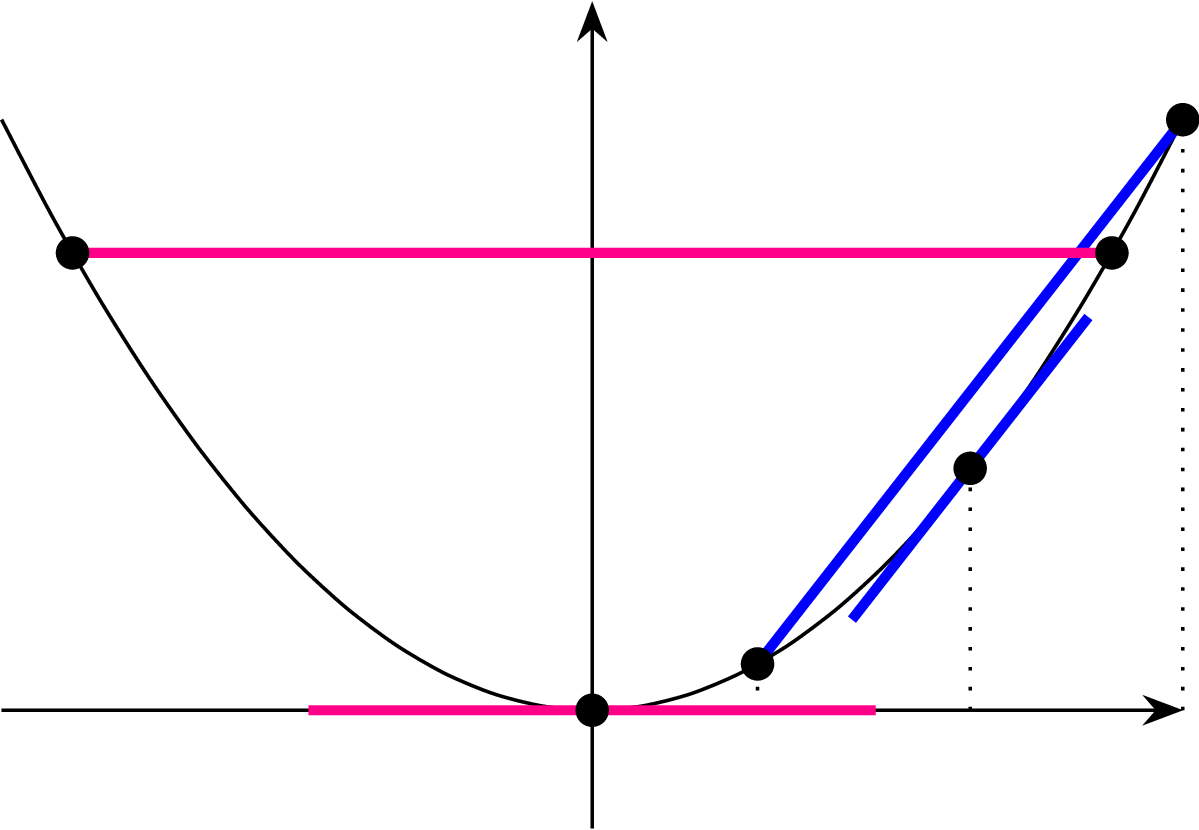
Twierdzenie Lagrange’a dla trójmianów. Łatwo sprawdzić, że specyficznie zachowuje się pod tym względem funkcja określona trójmianem kwadratowym. Istotnie, rozważając funkcję \(f \colon [x_1,x_2] \to \mathbb R\) określoną wzorem \(f(x) = ax^2 + bx + c,\) mamy \[\frac{f(x_2)-f(x_1)}{x_2-x_1} = \frac{a(x_2^2-x_1^2)+b(x_2-x_1)}{x_2-x_1} = a(x_2+x_1)+b \ \ \ \text{oraz} \ \ \ f'(x) = 2ax+b,\] dla wszelkich \(x \in (x_1,x_2).\) Pozwala to zauważyć, że punktem \(x_0\) ,,realizującym” (dodajmy, że w przypadku \(a \neq 0\) jedynym) poszukiwaną styczną, równoległą do prostej \(\ell\) przechodzącej przez punkty \((x_1,f(x_1))\) oraz \((x_2,f(x_2)),\) jest średnia arytmetyczna liczb \(x_1\) i \(x_2.\) Przykładu może tu dostarczyć funkcja przyporządkowująca argumentowi \(x\) wartość \(x^2\) (por. rys. 2).
Rys. 2. Wykres funkcji \(f(x) = x^2,\) jego dwie sieczne i odpowiadające im styczne. W obu przypadkach punkt \(x_0 = \frac{x_1+x_2}{2}\) zadaje jedyną możliwą styczną
A w drugą stronę? Naturalnym wydaje się pytanie, dla jakich jeszcze funkcji zachodzi taka prawidłowość, że szukaną styczną równoległą do zadanej siecznej jest ta, która za odciętą punktu styczności ma średnią arytmetyczną odciętych punktów, przez które poprowadzono sieczną.
Okazuje się, że tylko trójmiany mają tę właściwość. Dokładniej, w klasie funkcji różniczkowalnych \(f \colon \mathbb R\to\mathbb R\) równanie \[\label{eq:E}\tag{E} \frac{f(x)-f(y)}{x-y}=f'\biggl(\frac{x+y}{2}\biggr) \ \ \ \text{dla } x,y\in\mathbb R, \ x\neq y\] spełniają jedynie wielomiany stopnia co najwyżej \(2.\)
Nie jest trudno to udowodnić. Wiemy już, że równanie \(\eqref{eq:E}\) jest spełnione przez trójmiany kwadratowe, można więc bez straty ogólności przyjąć, że \(f(0) = 0\) oraz \(f'(0) = 0\) (w przeciwnym przypadku odjęlibyśmy od \(f\) funkcję liniową \(f(0) + xf'(0)\)). Podstawiając \(y=0\) w równaniu \(\eqref{eq:E}\), otrzymuje się \[\frac{f(x)-f(0)}{x}=f'\left( x/2 \right) \ \ \ \text{dla } x \neq 0,\] co dzięki założeniu \(f(0) = 0\) oznacza równość \[f(x) = xf'(x/2) \ \ \ \text{dla wszystkich } x \in \mathbb R.\] Podstawienie jej do \(\eqref{eq:E}\) prowadzi do: \[\frac{x f'(x/2) - y f'(y/2)}{x-y} = f'\biggl( \frac{x+y}{2} \biggr).\] Dla uproszczenia zapisu rozważmy pomocniczo funkcję \(G(x) := f'(x/2).\) Zgodnie z założeniem mamy \(G(0) = 0,\) a równanie wyżej daje nam \[\label{eq:E1}\tag{E1} xG(x)-yG(y)=(x-y)G(x+y) \ \ \ \text{dla } x,y \in \mathbb R.\] Podstawiając \(y=-x,\) uzyskuje się, że funkcja \(G\) jest nieparzysta. Teraz wystarczy w równaniu \(\eqref{eq:E1}\) w miejsce \(y\) przyjąć \(-y,\) żeby po wykorzystaniu nieparzystości otrzymać \[\label{eq:E2}\tag{E2} xG(x)-yG(y)=(x+y)G(x-y) \ \ \ \text{dla } x,y \in \mathbb R.\] Równania \(\eqref{eq:E1}\) i \(\eqref{eq:E2}\) prowadzą do: \[(x-y)G(x+y)=(x+y)G(x-y) \ \ \ \text{dla } x,y\in\mathbb R.\] Zauważmy, że wartości \(s = x+y\) oraz \(t = x-y\) możemy wybrać dowolnie (biorąc \(x=\frac{s+t}{2}\) i \(y=\frac{s-t}{2}\)), a więc \(tG(s)=sG(t)\) dla wszystkich \(s,t \in \mathbb R,\) co oznacza, że \(G(x)/x\) jest funkcją stałą.
Redukcja rozważań do przypadku \(f(0) = f'(0) = 0\) jest wygodna, ale nie jest konieczna – zachęcam Czytelnika do przekonania się, jak dalsze rozumowanie przebiega bez tej redukcji.
Dowiedliśmy w ten sposób, że dla pewnej stałej \(a \in \mathbb R\) zachodzi tożsamość \(G(x) = ax.\) Zgodnie z definicją \(G\) oznacza to \(f'(x) = 2ax,\) co w połączeniu z warunkiem \(f(0) = 0\) daje \(f(x) = ax^2,\) a więc trójmian kwadratowy.
Co dalej? Nieco więcej trudu kosztuje uzyskanie opisu rozwiązań równania \[\frac{f(x)-g(y)}{x-y}=h(x+y) \ \ \ \text{dla } x,y \in \mathbb R, \ x \neq y.\] Zadanie jest dużo ogólniejsze, ale jego rozwiązanie wymaga tylko nieco więcej trudu i jest bardzo podobne do rozwiązania równania \(\eqref{eq:E}\). Okazuje się, że jeśli funkcje \(f,g,h \colon \mathbb R\to\mathbb R\) spełniają powyższe równanie, to istnieją takie liczby \(a,b,c\in\mathbb R,\) że \[f(x) = ax^2 +bx+c = g(x) \ \ \ \text{oraz} \ \ \ h(x) = ax+b.\]
Czytelnik łatwo zauważy, że po dodaniu więzów \(f(x) = g(x)\) oraz \(h(x) = f'(x/2)\) problem obok przybiera postać równania \(\eqref{eq:E}\).
W uzyskaniu opisu rozwiązań powyższego równania kluczowym jest uzyskać równość \(f(x)=g(x)\) dla \(x\neq 0.\) W tym celu zauważmy, że \[\begin{aligned} \frac{f(x)-g(y)}{x-y} & = h(x+y) = h(y+x) \\&= \frac{f(y)-g(x)}{y-x} \ \ \ \text{dla } x \neq y, \end{aligned}\] co w konsekwencji daje \[f(x)-g(x) = g(y)-f(y) \ \ \ \text{dla } x \neq y.\] Podstawiając za \((x,y)\) pary \((z_1,z_2),\) \((z_2,z_3),\) \((z_3,z_1),\) otrzymujemy równość \(f(x) = g(x)\) dla wszystkich \(x.\) Do rozwiązania pozostaje równanie \[\frac{f(x)-f(y)}{x-y} = h(x+y) \ \ \ \text{dla } x,y \in \mathbb R, \ y \neq 0, \ x \neq y,\] które rozwiązujemy… tak jak poprzednio! Okazuje się, że powiązanie prawej strony równania z pochodną funkcji \(f\) nie było w rozumowaniu konieczne i nadal jesteśmy w stanie otrzymać wzór określający funkcje \(f\) i \(h.\)