Zapewne każdy Czytelnik ma konto w jakimś systemie bądź serwisie internetowym. Czasem to systemy automatycznie nadają nam identyfikator (nazywany też loginem), innym razem możemy wybrać go samodzielnie. Niezależnie od metody identyfikator musi być unikatowy. Dlatego jeśli samodzielnie możemy zaproponować swój login, to system sprawdza i informuje nas, czy jest on dostępny. Z perspektywy użytkownika to nic niezwykłego – zwykłe sprawdzenie, czy dany element figuruje w bazie. Co więcej, wiemy, że elementy w tej bazie są unikalne. Jednak choć proste podejście może działać w małych zbiorach, w skali globalnych sieci społecznościowych problem staje się znacznie bardziej złożony.
W 2019 roku Gmail obsługiwał ponad półtora miliarda kont. W 2023 roku Facebook raportował prawie 3 miliardy aktywnych użytkowników miesięcznie. Gdy pomyślimy, jak w takiej liczbie loginów zapewnić ich unikalność, sprawa przestaje być trywialna. Spróbujmy oszacować, ile miejsca zajmują takie dane. Zakładając, że login składa się wyłącznie ze znaków alfanumerycznych, a jego średnia długość wynosi \(N,\) to otrzymujemy \(3 \times 10^9 \times N\) znaków. Przy przechowywaniu wszystkich identyfikatorów jako zwykłe ciągi znaków daje to około \(3 \times N\) GB danych.
Większość informatyków zna struktury danych, takie jak drzewa czy tablice asocjacyjne, które umożliwiają wydajne zarządzanie zbiorami – odpowiadając na pytanie, czy dany element należy do zbioru, oraz pozwalając go dodawać i usuwać. O ile takie struktury optymalizują koszt dostępu, to ceną za to jest zwiększone zapotrzebowanie na pamięć.
W zarządzaniu projektami często mówi się o triadzie: czas, zakres, koszt – z których można zoptymalizować tylko dwie wartości jednocześnie. W potocznym rozumieniu: szybko, dobrze i tanio, ale nie możemy mieć wszystkiego na raz. Typowe struktury danych najczęściej optymalizują czas i koszt, zachowując stały zakres, czyli gwarancję, że dane nie zostaną utracone. A co by było, gdybyśmy zgodzili się na niewielki kompromis: pozwolili strukturze odpowiadać na pytanie o obecność elementu z pewnym marginesem niepewności? Innymi słowy, zaakceptowali odpowiedzi w rodzaju: „na pewno nie” albo „być może tak”.
W przypadku nazw użytkowników takie podejście jest akceptowalne. Jeśli system zasugeruje, że login być może jest już używany, użytkownik po prostu wymyśli inny. Tak długo, jak poziom pewności będzie wysoki, nikt nie zauważy różnicy.
Struktury, które optymalizują czas i koszt, poświęcając zakres, nazywamy probabilistycznymi strukturami danych. Jedną z nich jest filtr Blooma, zaprojektowany w 1970 roku przez Burtona Blooma. Filtr ten odpowiada na pytanie, czy element na pewno nie znajduje się w zbiorze.
Filtr Blooma wykorzystuje tablicę bitów i zestaw funkcji skrótu. Podstawowa koncepcja przypomina tablice asocjacyjne, ale zamiast zapisywać każdy element pod wskazanym indeksem i rozwiązywać kolizje, filtr używa kilku różnych funkcji skrótu.
Funkcja skrótu (inaczej funkcja mieszająca lub haszująca) to funkcja, która dla zadanej wartości przyporządkowuje jej jakąś liczbę z ograniczonego przedziału – skrót. Na przykład ciąg znaków zamienia na liczbę naturalną mniejszą od 100. Oczekujemy przy tym, że funkcja skrótu będzie zachowywała się „losowo” – drobna zmiana wartości wejściowej powoduje „niekontrolowaną” zmianę przypisanego skrótu.
Formalnie, filtr Blooma składa się z tablicy bitów o rozmiarze \(m\) oraz \(k\) funkcji skrótu \((f_1, \dots, f_k),\) które zwracają wartości z zakresu \([0, m-1].\) Na początku wszystkie bity w tablicy są ustawione na \(0.\) Gdy dodajemy nowy element, obliczamy jego skróty i ustawiamy bity na odpowiednich pozycjach w tablicy na \(1,\) tj. jeśli \(f_i(x) = j,\) to ustawiamy wartość \(j\)-tego bitu na \(1.\) Sprawdzanie obecności elementu również zaczynamy od obliczenia wartości wszystkich \(k\) funkcji skrótu. Jeśli choć jeden z odpowiadających im bitów ma wartość \(0,\) możemy z całą pewnością stwierdzić, że elementu nie ma w zbiorze. Jeśli wszystkie wskazane bity są ustawione na \(1,\) nie możemy być pewni odpowiedzi – element może być obecny lub może to być wynik kolizji.
Zobaczmy przykład działania filtru Blooma – do początkowo pustego zbioru dodajemy kilka elementów.
| element | \(f_1\) | \(f_2\) | \(f_3\) | filtr Blooma |
0000000000000 |
||||
| xyz | 2 | 7 | 12 | 0010000100001 |
| abc | 7 | 4 | 0 | 1010100100001 |
| foo | 10 | 1 | 5 | 1110110100101 |
| bar | 12 | 0 | 7 | 1110110100101 |
Jak widzimy, powyższy algorytm jest bardzo prosty, a przy odpowiednim doborze funkcji skrótu i parametrów również efektywny w implementacji. Pozwala także zaoszczędzić bardzo dużo pamięci, gdyż zamiast przechowywać pełne dane – utrzymujemy tylko tablicę bitów. Złożoność dodawania i sprawdzania, czy element należy do zbioru, to \(O(k),\) gdzie \(k\) jest liczbą użytych funkcji skrótu. Warto zauważyć, że rozmiar użytej pamięci nie zależy od samych danych, a jedynie od zbioru wartości funkcji skrótu \([0, m - 1].\) Jednak wraz ze wzrostem liczby elementów zbioru (\(n\)) rośnie liczba bitów o wartości \(1,\) a więc również prawdopodobieństwo \(p\) odpowiedzi fałszywie pozytywnej. Natomiast nigdy nie pojawią się fałszywie negatywne.
Spróbujmy teraz oszacować, jak duża powinna być tablica bitów i ile funkcji skrótu należy użyć, aby zapewnić odpowiednio wysoką precyzję, czyli odpowiednio niskie prawdopodobieństwo \(p.\) Załóżmy, że dodajemy nowy element \(x\) do zbioru i obliczamy jego skróty. Dla pierwszej funkcji skrótu \(f_1,\) dowolnego innego elementu \(y\) ze zbioru oraz wybranej funkcji \(f_j\) prawdopodobieństwo, że \(f_1(x) = f_j(y),\) wynosi \(\frac{1}{m},\) gdzie \(m\) to rozmiar tablicy bitów. Oznacza to, że z prawdopodobieństwem \(1 - \frac 1m\) bit \(f_1(x)\) nie koliduje z \(f_j(y).\) Jeśli w naszym zbiorze mamy \(n\) elementów i dla każdego obliczyliśmy \(k\) funkcji skrótu, to z niezależności wartości funkcji skrótu otrzymujemy, że z prawdopodobieństwem \(\left(1 - \frac 1m\right)^{nk}\) bit \(f_1(x)\) nie koliduje z żadnym z \(n\) elementów zbioru, a więc z prawdopodobieństwem \(1 - \left(1 - \frac 1m\right)^{nk}\) bit \(f_1(x)\) był już wcześniej ustawiony na \(1.\) Skoro używamy \(k\) niezależnych funkcji skrótu, to prawdopodobieństwo, że wszystkie obliczone bity \(f_1(x), f_2(x), \ldots, f_k(x)\) są już ustawione na \(1,\) wynosi \[\tag{1} p = \left(1 - \left(1 - \frac 1m\right)^{nk}\right)^k. \label{eq:precision}\] Zastanówmy się, czy możemy w jakiś łatwy sposób oszacować to prawdopodobieństwo. Jako że szukamy dobrej struktury danych dla bardzo dużych zbiorów, możemy rozpatrywać przypadek graniczny, w którym \(m\to\infty.\) Wytrawny Czytelnik na pewno widzi pewne podobieństwo między wzorem (1) a jedną z fundamentalnych własności liczby \(e,\) a konkretnie \[e^{-1} = \lim_{m\to\infty} \left( 1-\frac{1}{m} \right)^m.\] Zapisując \[\left(1-\frac{1}{m}\right)^{nk} = \left(\left(1-\frac{1}{m}\right)^m\right)^\frac{nk}{m} \approx \left(e^{-1}\right)^{\frac{nk}m} = e^{-\frac{nk}m},\] możemy oszacować \(p \approx (1-e^{\frac{-nk}{m}})^k.\)
Aby odpowiedzieć sobie na pytanie, ilu funkcji skrótu potrzebujemy, należy zastanowić się, jakiego prawdopodobieństwa odpowiedzi fałszywie pozytywnej (\(p\)) oczekujemy, oraz oszacować liczbę elementów w zbiorze (\(n\)) i dostępny rozmiar tablicy (\(m\)), w której zaimplementujemy filtr Blooma. Wyznaczmy najpierw minimum funkcji \(p(k)\) dla ustalonej wartości stosunku \(\frac m n.\) Mamy: \[p(k) \approx \left(1-e^{-\frac{nk}{m}}\right)^k = e^{\ln{\left(1-e^{-\frac{nk}{m}}\right)^k}} = e^{k\ln{\left(1-e^{-\frac{nk}{m}}\right)}}.\] Wystarczy teraz przyrównać do 0 pochodną wykładnika w wyrażeniu po prawej stronie powyższej równości (tzn. logarytmu naturalnego z funkcji \(p(k)\)): \[\left(k\ln\left(1-e^\frac{-nk}{m}\right)\right)' = \ln\left(1-e^\frac{-nk}{m}\right) + k\frac{\frac{n}{m}e^\frac{-nk}{m}}{1-e^\frac{-nk}{m}}.\] Zamiast szukać miejsca zerowego pochodnej dla dodatniego \(k,\) wygodniej jest podstawić \(q = e^\frac{-nk}{m},\) czyli \(\ln{q} = \frac{-nk}{m}.\) Wtedy otrzymujemy do rozwiązania równanie: \[\ln({1-q})-\frac{q}{1-q}\ln{q} = 0,\] dla \(q\) należącego do przedziału \((0, 1).\)
Warto zauważyć, że to pytanie ilościowe, a nie jakościowe. Nie wiemy, jakich funkcji użyć.
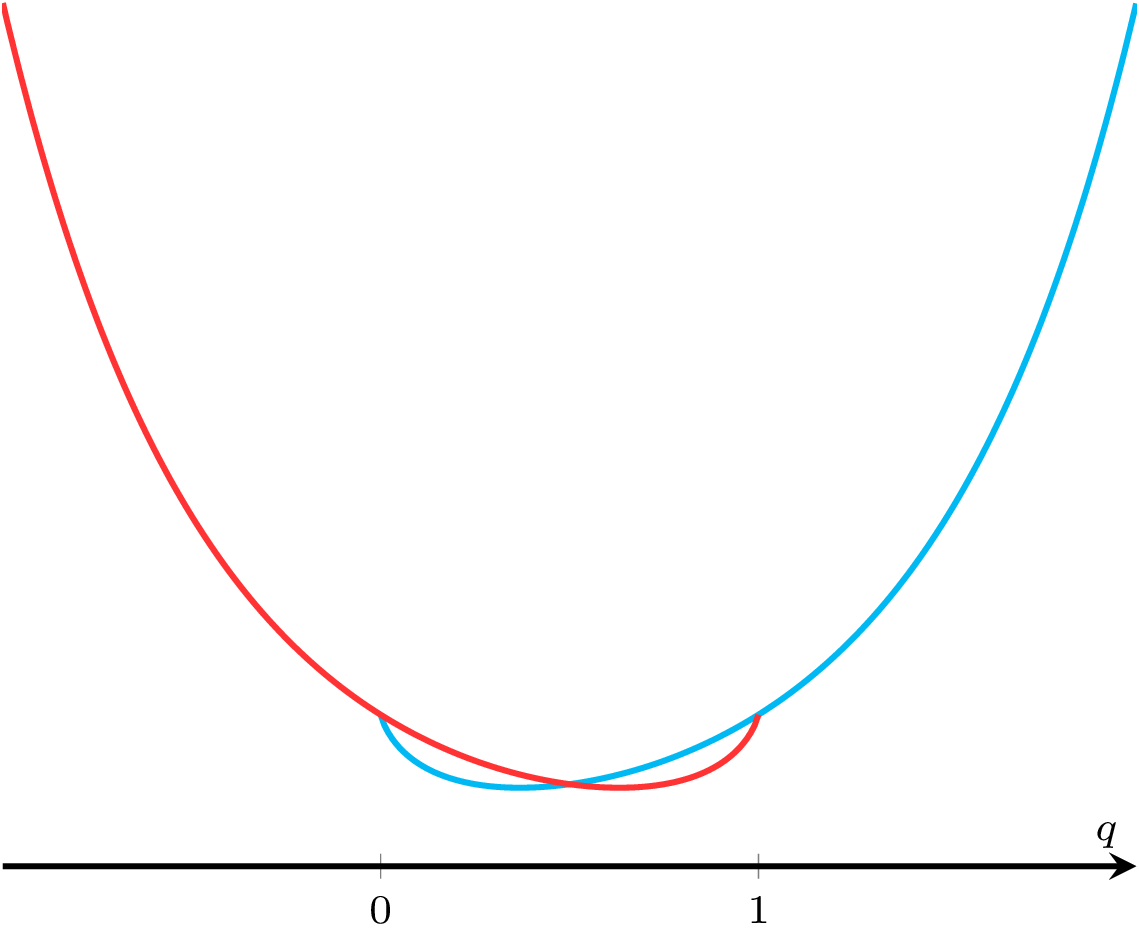
Powyższe równanie możemy przekształcić w następujący sposób: \[\begin{aligned} (1-q)\ln({1-q}) - q\ln{q} & = 0 , \\ \ln((1-q)^{1-q}) - \ln(q^q) & = 0, \\ \ln\left(\frac{(1-q)^{1-q}}{q^q}\right) & = 0 , \\ \frac{(1-q)^{1-q}}{q^q} & = 1 , \\ \textcolor{red}{(1-q)^{1-q}} & = {\color{cyan}{q^q}} . \end{aligned}\] Ponieważ funkcje \(q^q\) oraz \((1 - q)^{1 - q}\) są symetryczne względem punktu \(\frac 12,\) otrzymujemy \(q = \frac{1}{2},\) czyli \(e^\frac{-nk}{m} = \frac{1}{2},\) co oznacza, że \(p(k)' = 0\) dla \(k = \frac{m}{n}\ln2.\)
Porównanie funkcji \(q^q\) oraz \((1 - q)^{1 - q}\)
Co więcej, Czytelnik łatwo uzasadni widoczny na rysunku fakt, że dla \(0 < q < \frac 12\) mamy \(q^q < (1 - q)^{1 - q},\) zaś dla \(\frac 12 < q < 1\) zachodzi \(q^q > (1 - q)^{1 - q}.\) Oznacza to, że dla \(q < \frac 12\) (czyli \(k > \frac{m}{n}\ln2\)) mamy \(p(k)' > 0\) i podobnie dla \(k < \frac{m}{n}\ln2\) mamy \(p(k)' < 0.\) Stąd wnioskujemy, że dla \(k = \frac{m}{n}\ln2\) funkcja \(p\) osiąga swoje minimum.
Ponieważ jesteśmy w stanie uzależnić optymalną liczbę funkcji skrótu \(k\) od \(\frac{m}{n},\) nic nie stoi na przeszkodzie, aby obliczyć, jakiego rozmiaru tablicy potrzebujemy do przechowania \(n\) elementów z zadanym prawdopodobieństwem odpowiedzi fałszywie pozytywnej \(p\): \[\begin{aligned} p & = \left(1-e^{-n\frac{\frac{m}{n}}{m}\ln2}\right)^{{\frac{m}{n}}\ln2} = 2^{-\frac{m}{n}\ln2}, \\ m & = \frac{n}{\ln2}\log_\frac{1}{2}{p}. \end{aligned}\]
Dla naszego przykładu, w którym Facebook sprawdza loginy \(n = 3 \times 10^9\) użytkowników, jeśli chcemy uzyskać \(p=0{,}001,\) to potrzebujemy zaledwie \({k=10}\) funkcji oraz raptem \(m\approx5\text{GB}\) danych.
Jak widać na powyższym przykładzie, filtr Blooma pozwala znacząco zmniejszyć zużycie danych oraz utrzymać stały czas odpowiedzi, o ile jesteśmy w stanie zaakceptować pewien margines błędu.