Afiliacja: Wydział Matematyki i Nauk Informacyjnych, Politechnika Warszawska

Każdy, kto ma rodzeństwo, w dzieciństwie doskonale musiał opanować sztukę dzielenia się. Jak sprawiedliwie podzielić między siebie kawałek ciasta? Dla uproszczenia sytuacji, załóżmy najpierw, że w podziale uczestniczą dwie osoby: Alicja i Basia. Naturalnym rozwiązaniem, często stosowanym w praktyce, jest metoda „ja kroję, ty wybierasz”. Alicja kroi ciasto na dwa kawałki, zaś Basia wybiera swój kawałek jako pierwsza. Oczywiście w interesie Alicji jest, aby kawałki były możliwie równe, czyli by wartość mniejszego była jak największa. Wtedy jeśli Alicja dostanie kawałek, który jej nie zadowala, może mieć pretensje tylko do siebie.

Co ciekawe, podejście „ja kroję, ty wybierasz” jest znane od bardzo dawna. Już w Biblii, a dokładniej w Księdze Rodzaju, możemy znaleźć fragment o tym, jak Abram i Lot podzielili między siebie Ziemię Obiecaną, aby uniknąć konfliktów:

„Kraj nie mógł utrzymać ich obu, bo zbyt liczne mieli trzody; musieli więc się rozłączyć. A gdy wynikła sprzeczka, (…) rzekł Abram do Lota: Niechaj nie będzie sporu między nami, (…) bo przecież jesteśmy krewni. Wszak cały ten kraj stoi przed tobą otworem. Odłącz się ode mnie! Jeżeli pójdziesz w lewo, ja pójdę w prawo, a jeżeli ty pójdziesz w prawo, ja – w lewo. (…) Lot wybrał sobie zatem całą tę dolinę Jordanu i wyruszył ku wschodowi, i tak rozłączyli się obaj. Abram pozostał w ziemi Kanaan, Lot zaś zamieszkał w owej okolicy”. [Rdz 13, 6-12] (cytat z Biblii Tysiąclecia).

Co jednak zrobić, jeśli w podziale uczestniczy więcej osób? Pytanie to w pierwszej połowie XX wieku zadał Hugo Steinhaus swoim studentom, Stefanowi Banachowi i Bronisławowi Knasterowi. Dało to początek tak zwanej teorii sprawiedliwych podziałów, która jest dziś bogatą dziedziną, leżącą na styku matematyki, informatyki i ekonomii.

Dobra podzielne i niepodzielne

Problem dzielenia ciasta jest stosunkowo łatwy, gdyż ciasto ma następującą przyjemną cechę (poza innymi oczywistymi zaletami): można je podzielić/przekroić w dowolnym miejscu. My zajmiemy się problemem trudniejszym, gdy musimy rozdzielić dobra niepodzielne. Wyobraźmy sobie, że drużyna poszukiwaczy przygód, po pokonaniu smoka, odkryła jego skarb, który składa się z wielu cennych przedmiotów. Każdy przedmiot sam w sobie jest niepodzielny, czyli jedna osoba powinna go wziąć w całości. Dodatkowo każdy z uczestników wyprawy inaczej ceni poszczególne przedmioty: magiczny łuk ma niewielką wartość dla krasnoluda, ale elfi tropiciel będzie nim zdecydowanie zainteresowany. Inne przykładowe scenariusze, gdzie mamy do czynienia z podziałem zbioru niepodzielnych dóbr, to podział majątku po rozwodzie lub podział spadku. Formalnie dany mamy pewien zbiór przedmiotów \(V\) oraz \(n\) osób, zwanych zwyczajowo agentami. Ponadto dla każdego agenta dana jest jego funkcja użyteczności, która każdemu przedmiotowi przypisuje pewną nieujemną wartość. Funkcję użyteczności \(i\)-tego agenta będziemy oznaczać przez \(u_i.\)

Ciekawy przykład ścisłego podejścia do sprawiedliwego podziału spadku został zilustrowany w książce Cryptonomicon Neala Stephensona, którą Czytelnikom polecamy.

Niech \(\mathcal{P}_n(V)\) będzie rodziną wszystkich podziałów zbioru \(V\) pomiędzy \(n\) agentów; nie zakładamy tutaj, że zbiory w tym podziale muszą być niepuste. Każdy taki podział jest zatem ciągiem \((P_1\ldots,P_n),\) gdzie \(P_i\) jest podzbiorem \(V,\) który dostanie agent numer \(i.\) W tym artykule będziemy zakładać, że każda funkcja \(u_i\) jest addytywna, czyli wartością zbioru \(S \subseteq V,\) ozn. \(u_i(S),\) jest suma wartości jego elementów, czyli \(\sum_{v \in S} u_i.\) Przy tym założeniu wartość uzyskana przez \(i\)-tego agenta w podziale \((P_1,\ldots,P_n) \in \mathcal{P}_n(V)\) wynosi \(\sum_{v \in P_i} u_i(v).\) Zwróćmy uwagę, że założenie o addytywności nie zawsze jest spełnione w rzeczywistych sytuacjach.

Naszym celem jest znalezienie takiego podziału, aby każdy agent był zadowolony z wartości uzyskanych przedmiotów. Inaczej mówiąc, znalezienie podziału, który jest sprawiedliwy.

Co to jest „sprawiedliwy podział”?

Najbardziej naturalnym kryterium sprawiedliwości jest proporcjonalność: \(i\)-ty agent chciałby uzyskać przedmioty o łącznej wartości co najmniej \(u_i(V)/n.\) Nietrudno jednak przekonać się, że proporcjonalne podziały nie zawsze istnieją. Na przykład: jeśli jeden przedmiot istotnie przewyższa wartością pozostałe, może go dostać tylko jeden agent, a pozostali odejdą w poczuciu krzywdy. Badano więc wiele innych, mniej restrykcyjnych, definicji sprawiedliwego podziału, w nadziei na znalezienie takiej, która z jednej strony odzwierciedli intuicyjne poczucie sprawiedliwości, zaś z drugiej strony, zagwarantuje istnienie
rozwiązania.

W niniejszym artykule zajmiemy się stosunkowo nowym kryterium sprawiedliwości zaproponowanym przez Budisha [3] w 2011 roku, które bardziej pasuje do podziałów zbioru niepodzielnych dóbr. Nazwijmy je kryterium maksyminimalnego udziału. Dalej będziemy je nazywać w skrócie kryterium mms. Najpierw każdy agent przeprowadza następujący eksperyment myślowy: co by było, gdybyśmy mieli podzielić się zgodnie z metodą „ja kroję, ty wybierasz?”. Zatem każdy agent rozważa wszystkie podziały \(V\) na \(n\) części i wybiera taki, gdzie wartość najgorszej części (według jego funkcji użyteczności) jest jak największa. Wartość ta będzie oznaczana przez \(\mathsf{mms}_i,\) gdzie \(i\) jest numerem agenta. Formalnie mamy więc \[\mathsf{mms}_i = \max_{(P_1,\ldots,P_n) \in \mathcal{P}_n(V)} \min_{j \in \{1,\ldots,n\}} u_i(P_j).\] Podział, który realizuje maksimum w wyrażeniu powyżej, nazywamy mms-podziałem dla agenta \(i.\) Podział, gdzie dla każdego \(i\) agent \(i\)-ty uzyskuje przedmioty o łącznej wartości co najmniej \(\mathsf{mms}_i,\) będziemy uznawać za sprawiedliwy. Formalnie podział \((P_1,\ldots,P_n)\) jest mms-sprawiedliwy, jeśli dla każdego \(i\) zachodzi nierówność \(u_i(P_i) \geq \mathsf{mms}_i.\)

Skrót mms pochodzi od anglojęzycznej nazwy tego kryterium: maximin share.

Intuicyjnie każdy agent realistycznie (czy też pesymistycznie) ocenia to, na co może liczyć, zatem można spodziewać się, że tak niewygórowane oczekiwania uda się zaspokoić. Zauważmy też, że jeśli \((P_1,\ldots,P_n)\) jest mms-podziałem dla \(i\)-tego agenta, to \[u_i(V) = \sum_{j =1}^n u_i(P_j) \geq \sum_{j =1}^n \mathsf{mms}_i = n \cdot \mathsf{mms}_i,\] czyli w szczególności \(\mathsf{mms}_i \leq u_i(V)/n.\)

Zwróćmy uwagę, że każdy agent, obliczając swoją wartość \(\mathsf{mms}_i,\) przyjmuje pesymistyczny scenariusz, że każdy inny agent ceni wszystkie przedmioty tak jak on sam. Może się więc okazać, że istnieją podziały, w których każdy agent dostaje zbiór o wartości znacznie przewyższającej jego oczekiwania. Ekstremalnym przykładem jest sytuacja z dwoma agentami i dwoma przedmiotami \(a\) i \(b,\) gdzie agent 1 przypisuje wartość 1 przedmiotowi \(a\) i 0 przedmiotowi \(b,\) natomiast agent 2 odwrotnie – wartość 1 przedmiotowi \(b\) i 0 przedmiotowi \(a.\) W takim przypadku wartość parametru \(\mathsf{mms}_i\) wynosi 0 dla obu agentów, a każdy z nich może otrzymać przedmiot o wartości 1.

Istnienie mms-sprawiedliwych podziałów

Czy tak zdefiniowane sprawiedliwe podziały zawsze istnieją? Odpowiedź na to pytanie nie jest oczywista, o czym świadczy fakt, że znalezienie tej odpowiedzi zajęło aż 3 lata od momentu zaproponowania kryterium mms. Zanim tę odpowiedź zaprezentujemy, pokażmy dwie proste obserwacje.

Po pierwsze, jeśli w podziale występuje \(n=2\) agentów, mms-sprawiedliwy podział zawsze istnieje. Istotnie, rozważmy następujący protokół postępowania. Pierwszy agent prezentuje swój mms-podział \((P_1,P_2).\) Drugi agent wybiera zbiór \(P_j\) \((j \in \{1,2\})\) o większej wartości według funkcji \(u_2\) (lub dowolny zbiór, jeśli wartości obu zbiorów są równe). Zauważmy, że wartość ta wyniesie co najmniej \(u_2(V)/2 \geq \mathsf{mms}_2,\) zatem drugi agent będzie zadowolony z uzyskanych przedmiotów. Pierwszy agent bierze zbiór, który pozostał – zauważmy, że on także będzie zadowolony, gdyż wartość jego zbioru wynosi co najmniej \(\min_{j \in \{1,2\}} u_1(P_j) = \mathsf{mms}_1.\)

Powyższą obserwację można nieco uogólnić na sytuację, kiedy agentów jest dowolnie wielu, ale wszyscy, z wyjątkiem być może jednego (powiedzmy pierwszego), mają tę samą funkcję użyteczności i, co za tym idzie, ten sam mms-podział \((P_1,\ldots,P_n).\) Agent pierwszy wybiera ten zbiór \(P_j,\) który maksymalizuje wartość \(u_1(P_j),\) zaś każdy z pozostałych agentów bierze jeden z pozostałych \(n-1\) zbiorów (każdy agent inny zbiór). Analogicznie do poprzedniego przypadku nietrudno zweryfikować, że przy takim podziale każdy z agentów odejdzie zadowolony.

Problem rozstrzygnięcia, czy mms-sprawiedliwe podziały dla więcej niż dwóch agentów zawsze istnieją, okazał się znacznie trudniejszy. Ostatecznie sprawdziła się tu maksyma wypowiedziana przez Nogę Alona (w kontekście innej hipotezy, która wydawała się oczywista, a okazała się nieprawdziwa: hipotezy Hedetniemiego): czasami powodem, że coś jest bardzo trudne do pokazania, jest to, że jest to nieprawda. Pierwszy przykład zbioru dóbr i funkcji użyteczności, dla których nie istnieje mms-sprawiedliwy podział, został skontrowany przez Kurokawę, Procaccia i Wanga [5]. Poniżej zaprezentujemy uproszczoną konstrukcję podaną przez Feigego, Sapira i Taubera [4]. Rozważmy zbiór przedmiotów \(V = \{1,\ldots,9\}\) i trzech agentów z następującymi funkcjami użyteczności.

Zauważmy, że \(u_1(V) = u_2(V) = u_3(V) = 120.\) Rozważmy następujące trzy podziały zbioru \(V\) na trzy podzbiory: \[\begin{aligned} \mathcal{P}_1 = & (\{1,6,8\},\{2,4,9\},\{3,5,7\}), \\ \mathcal{P}_2 = & (\{1,5,9\},\{2,6,7\},\{3,4,8\}), \\ \mathcal{P}_3 = & (\{1,4\},\{2,5,8\},\{3,6,7,9\}). \end{aligned}\] Pomocna przy ich analizie może być tabelka, gdzie w wierszu odpowiadającym podziałowi \(\mathcal{P}_i\) przedstawione są wagi przedmiotów dla \(i\)-tego agenta.

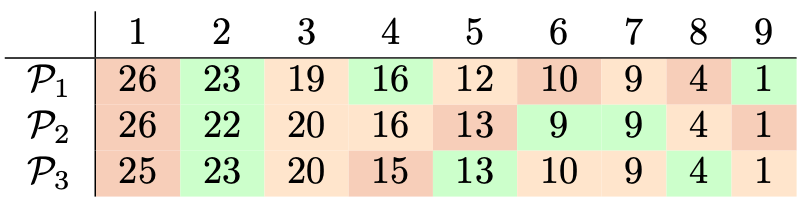
Zauważmy, że dla każdego \(i\) każdy zbiór w podziale \(\mathcal{P}_i\) ma dla \(i\)-tego agenta wartość 40. Ponieważ jest to dokładnie jedna trzecia wartości całego zbioru \(V,\) podział \(\mathcal{P}_i\) jest mms-podziałem dla \(i\)-tego agenta, czyli \(\mathsf{mms}_i = 40.\) Jednakże nietrudna, choć dość żmudna, analiza przypadków pozwala przekonać się, że w każdym podziale \((P_1,P_2,P_3) \in \mathcal{P}_3(V)\) istnieje \(i,\) dla którego \(u_i(P_i) \leq 39.\) Pokazuje to, że nie da się podzielić zbioru \(V\) w taki sposób, aby każdy z trzech agentów był zadowolony.

Powyższa konstrukcja pokazuje, że nie w każdej sytuacji mms-sprawiedliwy podział istnieje. Rozważmy jednak podział \(\mathcal{P} = (P_1,P_2,P_3),\) w którym \[P_1 = \{1,5,9\}, \ \ \ P_2 = \{2,6,7\}, \ \ \ P_3 = \{3,4,8\}.\] Pomocna może okazać się poniższa tabelka (w \(i\)-tym wierszu pokazane są odpowiednie wartości funkcji \(u_i\)).

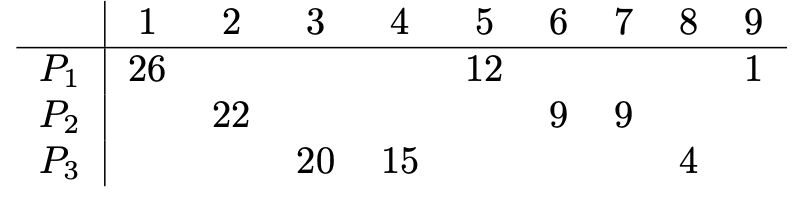
W tym podziale mamy \(u_1(P_1) = u_3(P_3)=39\) i \({u_2(P_2)=40}.\) Zatem pierwszy i trzeci agent, choć nie są w pełni zadowoleni, uzyskali prawie tyle, na ile liczyli. Czy można coś ciekawego powiedzieć o istnieniu takich prawie mms-sprawiedliwych podziałów? Wrócimy do tej myśli później, a tymczasem zmieńmy nieco temat.

Podziały grafów

W dotychczas analizowanym przez nas problemie nie występowały żadne związki między przedmiotami ze zbioru \(V,\) i dowolny zbiór przedmiotów był akceptowany przez agentów, o ile tylko miał dla nich odpowiednio dużą wartość. W praktycznych sytuacjach związki pomiędzy dobrami często mają znaczenie. Przykładem może być następujący problem pojawiający się w rolnictwie. Przez wiele pokoleń rolnicy dzielili swoje pola na coraz mniejsze kawałki między swoje, często bardzo liczne, potomstwo. W wyniku tego procesu, po latach, pola zostały podzielone na bardzo dużo bardzo małych kawałków, a poszczególni właściciele posiadają gospodarstwa złożone z wielu małych, często odległych od siebie poletek. Taka sytuacja nie sprzyja oczywiście racjonalnej gospodarce rolnej. W związku z tym dokonuje się ponownego podziału ziemi pomiędzy dotychczasowych właścicieli, czyli tzw. komasacji. Dla rolników istotna jest nie tylko wartość pól, które w wyniku tego podziału otrzymują, ale również to, aby każdy z nich miał pole w jednym kawałku.

Załóżmy więc, że zbiór dzielonych przedmiotów \(V\) jest zbiorem wierzchołków pewnego spójnego grafu \(G.\) Każdy z agentów ma funkcję użyteczności przypisującą wartości poszczególnym przedmiotom (dokładnie tak jak wcześniej). Teraz jednak każdy agent chciałby, aby otrzymane przez niego przedmioty tworzyły spójny podgraf grafu \(G.\) Wartość \(\mathsf{mms}_i\) jest też zdefiniowana względem podziałów \(V\) na \(n\) spójnych części.

Zdefiniujmy ten problem formalnie. Mamy dany graf \(G\) o zbiorze wierzchołków \(V\) oraz dla każdego \(i \in \{1,\ldots,n\}\) addytywną funkcję użyteczności \(u_i : V \to \mathbb{R}_{\geq 0}.\) Przez \(\mathcal{P}_n(G)\) oznaczmy rodzinę wszystkich uporządkowanych podziałów \(V,\) w których każdy zbiór podziału indukuje spójny podgraf \(G.\) Dla każdego \(i\) definiujemy: \[\mathsf{mm}s_i = \max_{(P_1,\ldots,P_n) \in \mathcal{P}_n(G)} \min_{j \in \{1,\ldots,n\}} u_i(P_j).\] Znowu: \(\mathsf{mm}s_i\) oznacza minimalną łączną wartość przedmiotów, po otrzymaniu których agent numer \(i\) będzie zadowolony. Podział \((P_1,\ldots,P_n) \in \mathcal{P}_n(G)\) nazywamy mms-sprawiedliwym podziałem grafu \(G\), jeśli każdy agent jest zadowolony, czyli dla każdego \(i\) zachodzi \(u_i(P_i) \geq \mathsf{mm}s_i.\) Problem rozważany w poprzedniej sekcji jest więc szczególnym przypadkiem aktualnego, gdy \(G\) jest grafem pełnym. Nietrudno też zweryfikować, że w aktualnie rozważanym wariancie nadal działa argumentacja dowodząca istnienia mms-sprawiedliwego podziału w sytuacji, gdy wszyscy agenci, z wyjątkiem być może jednego, mają identyczną funkcję użyteczności. Prowadzi nas to do pytania: Dla jakich grafów \(G\) możemy zagwarantować istnienie mms-sprawiedliwego podziału, niezależnie od liczby agentów i ich funkcji użyteczności?

Drzewa. Okazuje się, że przykładem rodziny grafów o takiej własności są drzewa, co zostało udowodnione przez Bouvereta i in. [2]. Naszkicujemy ten dowód, ale najpierw wprowadźmy oznaczenia. Niech \(T\) będzie drzewem o zbiorze wierzchołków \(V\) i rozważmy \(n\) agentów z funkcjami użyteczności \(u_i : V \to \mathbb{R}_{\geq 0},\) dla \(i \in \{1,\ldots,n\}.\) Wybierzmy dowolny wierzchołek \(r \in V,\) będziemy traktować go jako korzeń. Definiuje to dla każdej pary sąsiadujących wierzchołków relację rodzic–dziecko. Dla \(w \in V\) przez \(V_w\) oznaczać będziemy podzbiór \(V\) składający się z wierzchołka \(w\) i wszystkich jego potomków w drzewie \(T.\) Zauważmy, że zbiór \(V_w\) indukuje poddrzewo \(T\) ukorzenione w \(w,\) czyli w szczególności spójny podgraf \(T.\) Co więcej, graf uzyskany z \(T\) przez usunięcie wierzchołków z \(V_w\) jest spójny (dokładniej, jest drzewem).

Dowód istnienia mms-sprawiedliwego podziału jest indukcyjny po \(n.\) Jeśli \(n=1,\) czyli jest tylko jeden agent, sytuacja jest jasna: zgarnia on cały zbiór \(V.\) Niech więc \(n \geq 2\) i przypuśćmy, że każde drzewo ma mms-sprawiedliwy podział dla \(n-1\) agentów.

Zainicjujmy \(w = r.\) Następnie dla \(i=1,2,\ldots\) agent \(i\)-ty sprawdza, czy \(u_i(V_{w}) \geq \mathsf{mms}_i.\) Jeśli nie, nic się nie dzieje i przechodzimy do kolejnego agenta. W przeciwnym przypadku agent \(i\)-ty wskazuje wierzchołek \(w' \in V_{w}\) o następujących własnościach:

1. \(u_i(V_{w'}) \geq \mathsf{mms}_i\) oraz

2. spośród wszystkich wierzchołków spełniających pierwszą własność \(w'\) leży w drzewie \(T\) najniżej, czyli w największej odległości od korzenia (remisy rozstrzygamy dowolnie).

Wierzchołek \(w'\) zastępuje wierzchołek \(w\) i przechodzimy do kolejnego agenta.

Zauważmy, że w ciągu tej procedury na pewno któryś agent coś wskaże, bo w szczególności każdy byłby (bardzo) zadowolony, gdyby dostał zbiór \(V_r=V,\) rozpatrywany w pierwszym kroku. Teraz rozważmy wierzchołek zapisany jako \(w\) po ostatniej iteracji i niech \(i\) będzie numerem agenta, który go wskazał.

Agent \(i\) dostaje zbiór \(V_w,\) a dla pozostałych \({n-1}\) agentów i drzewa indukowanego przez \(V \setminus V_w\) otrzymujemy podział z założenia indukcyjnego. Dlaczego ten podział zbioru \(V\) jest mms-sprawiedliwy? Agent \(i\) na pewno będzie zadowolony, bo sam tak zadeklarował, wskazując wierzchołek \(w.\) Z drugiej strony dla każdego \(j \neq i\) zbiór \(V_w\) jest zawarty w jednym z bloków mms-podziału agenta \(j\) (dlaczego?). Oznacza to, że agent \(j\) w swoim mms-podziale liczy się z utratą zbioru \(V_w\) (a nawet jego nadzbioru). Nietrudno pokazać, że wynika z tego, że dla każdego agenta \(j \neq i\) najgorszy zbiór w jego mms-podziale drzewa indukowanego przez \(V \setminus V_w\) między \(n-1\) agentów ma wartość co najmniej \(\mathsf{mms}_i\) (gdzie wartość ta policzona jest dla całego zbioru \(V\) i \(n\) agentów). Zatem zbiór, przyznany mu w wywołaniu indukcyjnym, spełni jego oczekiwania.

Cykle. Zachęceni sukcesem w przypadku drzew spójrzmy na inne grafy o prostej strukturze. Naturalnym pierwszym kandydatem są cykle. Okazuje się jednak, że w tym wypadku mms-sprawiedliwe podziały mogą nie istnieć. Zaprezentujmy konstrukcję Bouvereta i in. [2]. Tym razem mamy osiem przedmiotów ułożonych w cykl zgodnie z naturalnym porządkiem. Agentów jest czworo, przy czym funkcje użyteczności agentów 1 i 2 są równe, podobnie agentów 3 i 4. Zauważmy, że funkcje te są „cyklicznie przesunięte” względem siebie.

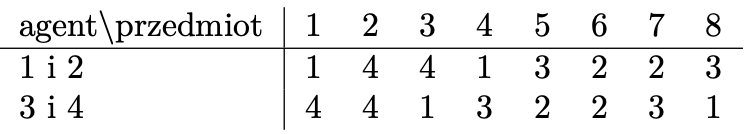
Rozważmy dwa podziały zbioru przedmiotów na cztery spójne bloki, przedstawione poniżej:

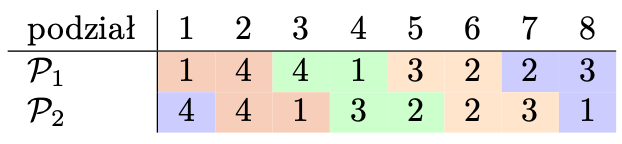
Zauważmy, że w podziale \(\mathcal{P}_1\) każdy agent dostaje jedną czwartą łącznej wartości wszystkich przedmiotów według funkcji użyteczności \(u_1=u_2,\) a w podziale \(\mathcal{P}_2\) każdy agent dostaje jedną czwartą łącznej wartości wszystkich przedmiotów według funkcji użyteczności \(u_3=u_4.\) Zatem podział \(\mathcal{P}_1\) jest mms-podziałem dla agentów 1 i 2, a podział \(\mathcal{P}_2\) jest mms-podziałem dla agentów 3 i 4. Dla każdego \(i\) wartość \(\mathsf{mms}_i\) wynosi więc 5.

Przypuśćmy, że w rozważanym przypadku istnieje mms-sprawiedliwy podział \(\mathcal{P}.\) W podziale tym każdy agent powinien dostać przedmioty, którym przypisuje wartość co najmniej 5. Skoro wartość każdego przedmiotu nie przekracza 4, w podziale \(\mathcal{P}\) każdy agent dostaje co najmniej dwa (czyli dokładnie dwa) przedmioty. Zatem \(\mathcal{P}\) jest albo podziałem \(\mathcal{P}_1,\) albo podziałem \(\mathcal{P}_2.\) Jest to sprzeczność, gdyż podział \(\mathcal{P}_1\) nie jest zadowalający dla jednego spośród agentów 3 i 4, a podział \(\mathcal{P}_2\) nie jest zadowalający dla jednego spośród agentów 1 i 2.

Zwróćmy uwagę, że konstrukcja dla cyklu nie oznacza, że jeśli graf \(G\) zawiera cykl o ośmiu wierzchołkach, to nie istnieje dla niego mms-sprawiedliwy podział. Co prawda, ustawiając wartości funkcji użyteczności dla wierzchołków spoza cyklu na 0, możemy zasygnalizować, że nie mają one wartości dla żadnego z agentów, ale te dodatkowe wierzchołki (i krawędzie) tworzą nowe połączenia, przez co rodzina rozważanych podziałów wierzchołków cyklu może być większa.

Co dalej?

Wspomnieliśmy wcześniej, że w zaprezentowanym przykładzie, gdzie nie istnieje mms-sprawiedliwy podział (dla grafu pełnego), każdy agent \(i\) otrzymuje przedmioty o sumarycznej wartości prawie równej swojej wartości \(\mathsf{mms}_i.\) Prowadzi to do następującego wariantu problemu. Niech \(\mathcal{G}\) będzie rodziną grafów. Wyznacz największą stałą \(\alpha_\mathcal{G} \in [0,1]\) (zależną tylko od \(\mathcal{G}\)), dla której prawdziwe jest następujące stwierdzenie: Jeśli przedmioty są wierzchołkami grafu z rodziny \(\mathcal{G},\) to niezależnie od liczby agentów i ich funkcji użyteczności istnieje podział gwarantujący każdemu agentowi \(i\) przedmioty, którym przypisuje on łączną wartość co najmniej \(\alpha_\mathcal{G} \cdot \mathsf{mms}_i.\) Zaprezentowana wcześniej konstrukcja pokazuje, że jeśli \(\mathcal{G}\) jest rodziną grafów pełnych, to \(\alpha_\mathcal{G} \leq \frac{39}{40}.\) Okazuje się, że w tym samym przypadku mamy \(\alpha_\mathcal{G} \geq \frac{3}{4}+\frac{3}{3836},\) co pokazali Akrami i Garg [1]. Tylko dla niewielu spośród innych klas grafów znane są podobne oszacowania.

Bibliografia

1. Akrami, H., & Garg, J. (2024). „Breaking the 3/4 barrier for approximate maximin share”. W Proceedings of the 2024 Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2024, str. 74–91.

2. Bouveret, S., Cechlárová, K., Elkind, E., Igarashi, A., & Peters, D. (2017). „Fair division of a graph”. W Proceedings of the 26th International Joint Conference on Artificial Intelligence, IJCAI 2017, str. 135–141.

3. Budish, E. (2011). „The combinatorial assignment problem: Approximate competitive equilibrium from equal incomes”. Journal of Political Economy, 119(6), str. 1061–1103.

4. Feige, U., Sapir, A., & Tauber, L. (2022). „A tight negative example for mms fair allocations”. W Proceedings of 17th International Conference, WINE 2021, str. 355–372.

5. Kurokawa, D., Procaccia, A. D., & Wang, J. (2018). „Fair enough: Guaranteeing approximate maximin shares”. Journal of the ACM, 65(2), str. 1–27.