Zadania z matematyki nr 913, 914
Termin nadsyłania rozwiązań: 31 III 2026
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
903 (\(WT = 1{,}45\)) i 904 (\(WT = 1{,}36\))
z numeru 6/2025
Jerzy Cisło Wrocław 46,09 Szymon Kitowski 43,92 Barbara Mroczek 43,05 Andrzej Daniluk Warszawa 40,76 Mikołaj Znamierowski 40,68 Marian Łupieżowiec Gliwice 38,54 Krzysztof Kamiński Pabianice 38,09 Roksana Słowik 37,51 Michał Adamaszek Kopenhaga 37,30 Stanisław Bednarek Łódź 37,24 Moment godny uwagi: pan Jerzy Cisło – 44 p. po raz osiemnasty!
Redaguje Marcin E. KUCZMA
913. Niech \(m\) będzie liczbą naturalną nieparzystą. Wyznaczyć największą możliwą liczność zbioru \(M,\) zawartego w przedziale \([-m,m],\) złożonego z liczb całkowitych, w którym każda trójka różnych liczb ma sumę różną od zera.
914. Znaleźć wszystkie pary \(a,b\) liczb rzeczywistych różnych od zera, dla których funkcja \({f\colon\mathbb R\to\mathbb R}\) dana wzorem \({f(x)=|\!\sin(ax)|+|\!\cos(bx)|}\) jest okresowa.
Zadanie 914 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązania zadań z numeru 9/2025
Przypominamy treść zadań:
905. Niech \(f(x)=x^3(x^2+1)^{-1}.\) Wyznaczyć wszystkie całkowite dodatnie wartości sumy \({f(a)+f(b)+f(c)}\) dla dowolnych liczb całkowitych \(a,b,c.\)
906. W przestrzeni (trójwymiarowej) dana jest parabola \(P.\) Niech \(R\) będzie zbiorem wszystkich punktów, będących wierzchołkami stożków obrotowych, na których leży \(P\) [przez stożek obrotowy rozumiemy tu powierzchnię powstałą przez obrót prostej wokół przecinającej ją (nie prostopadle) innej prostej (osi obrotu)].
Udowodnić, że zbiór \(R\) także jest parabolą oraz wyjaśnić, jak są usytuowane jej wierzchołek i ognisko względem wierzchołka i ogniska paraboli \(P.\) [Wierzchołek paraboli to punkt jej przecięcia z osią symetrii; ognisko to punkt (w jej płaszczyźnie) określony przez własność: każdy punkt paraboli jest jednakowo odległy od ogniska i od pewnej prostej (zwanej kierownicą)].
905. Z uwagi na równość \({f(x)=x-g(x)},\) gdzie \({g(x)=x(x^2+1)^{-1}},\) warunek zadania jest (dla liczb całkowitych \({a,b,c\ge1}\)) równoważny temu, by suma \({g(a)+g(b)+g(c)}\) była liczbą całkowitą. W przedziale \([1,\infty)\) funkcja \(g\) jest malejąca. Jej wartości dla argumentów \(1,2,3,4,5,\ldots\) wynoszą, kolejno: \[\tfrac12\,,\; \tfrac25\,,\; \tfrac3{10}\,,\; \tfrac4{17}\,,\; \tfrac5{26}\,,\;\ldots\,,\] więc jedyną możliwą całkowitą wartością wypisanej sumy jest \({g(a)+g(b)+g(c)=1}.\) Przyjmijmy (b.s.o.), że \({a\le{b}\le{c}}\,\); wówczas \({g(a)\ge g(b)\ge g(c)}\) oraz \({g(a)\ge{1\over 3}},\) czyli \({a=1}\) lub \({a=2}.\) Dalej, musi być \({g(b)\ge{1\over 2}(1-g(a))}.\) Dla \({a=1}\) oraz dla \({a=2}\) to daje, odpowiednio, \({g(b)\ge{1\over 4}}\) oraz \({g(b)\ge{3\over 10}}\,\); w obu przypadkach to oznacza, że \({b\le3}.\)
Pozostaje sprawdzić, czy dla uzyskanych par \((a,b)\) (\({{}=(1,1),\,(1,2),\,(1,3),\,(2,2),\,(2,3)}\)) różnica \({1-(g(a)+g(b))}\) jest możliwą wartością \(g(c).\) Jedynie dla \({a=2},\) \({b=3}\) tak jest; wtedy także \({c=3}\,\) i \({g(2)+g(3)+g(3)={2\over 5}+{3\over 10}+{3\over 10}=1},\) zaś \({f(2)+f(3)+f(3)=(2+3+3)-1=7}.\) To jedyna możliwa wartość sumy \({f(a)+f(b)+f(c)}.\)
906. Ustalmy kartezjański układ współrzędnych \(Oxyz,\) w którym parabola \(P\) jest dana równaniem \({y=x^2},\) \({z=0}\) (b.s.o, bo wszystkie parabole są podobne). Ma ona wierzchołek \({{\bf w}=(0,0,0)}\) i ognisko \({{\bf f}=(0,{1\over 4},0)}\) (kierownicą jest prosta \({x=z=0},\) \({y=-{1\over 4}}\)). Weźmy dowolny stożek obrotowy \(C,\) na którym leży \(P.\) Przyjmijmy, że wierzchołkiem stożka \(C\) jest punkt \({{\bf p}_0=(x_0,y_0,z_0)}.\) Oznaczmy przez \(\varphi\) miarę kąta ostrego między jego osią obrotu i tworzącą i niech \({c=\cos\varphi}\) (zatem \({0<c<1}\)). Niech \({{\bf u}=(u,v,w)}\) będzie wersorem kierunkowym osi obrotu, zorientowanym tak, by \({v>0}\) (wersor to wektor o długości 1).
Dowolnie wybrany punkt przestrzeni \({{\bf p}=(x, y,z)}\) leży na stożku \(C\) wtedy i tylko wtedy, gdy kąt między wektorami \({{\bf p}-{\bf p}_0}\) oraz \({\bf u}\) ma miarę \(\varphi\) lub \({\pi-\varphi}\); czyli gdy jego kosinus (dany znanym wzorem \({{{\bf u}\mathop{\lower-2pt\hbox{\bf.}}({\bf p}-{\bf p}_0)\over\Vert{\bf u}\Vert\cdot\Vert{\bf p}-{\bf p}_0\Vert}}\,\)) jest równy \(\pm{c}.\) Skoro \({\Vert{\bf u}\Vert=1},\) warunek ten po rozpisaniu na współrzędne przybiera postać \[\begin{aligned} u(x-x_0)+v(y-y_0)+w(z-z_0)\\[-2pt]=\pm{c}\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}. \end{aligned} \tag{1}\] Jest to więc równanie powierzchni stożka \(C.\) Parabola \(P\) leży na niej, jeśli po podstawieniu \({y=x^2},\) \({z=0}\) równanie (1) jest spełnione dla każdej liczby rzeczywistej \(x.\) Przez podniesienie stronami do kwadratu wnosimy, że zawieranie \({P\subset{C}}\) ma miejsce wtedy i tylko wtedy, gdy \[\begin{aligned} \bigl(u(x-x_0)+v(x^2-y_0)+w(-z_0)\bigr)^2\\=c^2\bigl((x-x_0)^2+(x^2-y_0)^2+z_0^2\bigr)\ \ \ \hbox{dla}\;x\in\mathbb R. \end{aligned} \tag{2}\] To równość dwóch wielomianów zmiennej \(x,\) czwartego stopnia. Przyrównując współczynniki przy \(x^4\) po lewej i prawej stronie, a następnie współczynniki przy \(x^3,\) dostajemy równości \({v^2=c^2},\) \({2uv=0}\); czyli (pamiętając, że \({v>0},\) \({c>0}\)): \({v=c},\) \({u=0}.\) Wstawiamy te wartości do (2) i po redukcji dostajemy równanie \[-2cwz_0(x^2-y_0)+w^2z_0^2=c^2(x-x_0)^2+z_0^2c^2. \tag{3}\] Kolejne przyrównanie współczynników, tym razem przy \(x^2\) oraz \(x^1,\) pokazuje, że \({-2cwz_0=c^2},\) \({-2c^2x_0=0},\) skąd \({wz_0=-{{1\over 2}}c},\) \({x_0=0}.\) Równanie (3) redukuje się do postaci \({-c^2y_0+\bigl(-{{1\over 2}}c\bigr)^2=c^2z_0^2},\) czyli \({y_0={1\over 4}-z_0^2}.\)
Zważywszy, że stożek \(C\) (zawierający parabolę \(P\)) był wybrany dowolnie, więc jego wierzchołek był dowolnym punktem zbioru \(R,\) widzimy, że zbiór \(R\) jest opisany równaniami \[x=0,\ \ \ \ y={1\over 4}-z^2.\] Jest zatem parabolą, leżącą w płaszczyźnie \({x=0},\) izometryczną z parabolą \(P.\) Jej wierzchołkiem jest punkt \({\widetilde{{\bf w}}=(0,{1\over 4},0)},\) a ogniskiem punkt \({\widetilde{{\bf f}}=(0,0,0)}\) (obraz ogniska paraboli \(P\) w tej izometrii). Pierwszy z nich pokrywa się z ogniskiem paraboli \(P,\) drugi z jej wierzchołkiem: \({\widetilde{{\bf w}}={\bf f}},\) \({\widetilde{{\bf f}}={\bf w}}.\) To właśnie usytuowanie, o które chodziło w zadaniu.
[Autor zadania, Janusz Fiett, zwrócił uwagę na artykuł Stożkowe (w \(\Delta^{12}_{13}\)), w którym jest opisana własność pozwalająca uprościć rozwiązanie: sfera wpisana w stożek, styczna do płaszczyzny przecinającej jego powierzchnię wzdłuż paraboli, ma punkt styczności z tą płaszczyzną będący ogniskiem tej paraboli. Zachęcamy Czytelników do zapoznania się z tym artykułem i do dopracowania rozwiązania tą metodą.]
Zadania z fizyki nr 810, 811
Termin nadsyłania rozwiązań: 31 III 2026
Redaguje Elżbieta ZAWISTOWSKA
810. Gładki, jednorodny sznurek o długości \(l\) i masie \(m\) przerzucony jest przez niewielki nieruchomy blok tak, że w chwili początkowej pozostaje w równowadze, a po lekkim przesunięciu zaczyna ześlizgiwać się z bloku. Znaleźć siłę nacisku sznurka na blok w chwili, gdy jego długość z jednej strony wynosi \(l/3.\)
811. Naładowany kondensator płaski znajduje się w jednorodnym polu magnetycznym, którego linie są prostopadłe do płaszczyzn okładek. Odległość między okładkami wynosi \(d,\) indukcja pola magnetycznego \(B.\) Wewnątrz kondensatora, koło ujemnie naładowanej okładki znajduje się źródło powolnych elektronów wysyłanych w różnych kierunkach. Jakie musi być napięcie między okładkami, aby elektrony ogniskowały się z możliwie najlepszą dokładnością na dodatnio naładowanej okładce? Oddziaływanie między elektronami zaniedbujemy.
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
800 (\(WT=2{,}55\)), 801 (\(WT=2{,}25\)) z numeru 6/2024
Jacek Konieczny Poznań 41,41 Jan Zambrzycki Białystok 4–39,00 Ryszard Woźniak Kraków 34,00 Andrzej Nowogrodzki Chocianów 3–32,28 Paweł Perkowski Ożarów Maz. 6–29,93 Krzysztof Zygan Lubin 26,89 Tomasz Wietecha Tarnów 18–21,64 Paweł Kubit Kraków 20,30 Marian Łupieżowiec Gliwice 3–14,49 Krzysztof Magiera Łosiów 4–13,42 Zbigniew Galias Kraków 1–12,77 Lista obejmuje uczestników ligi, których stan konta wynosi przynajmniej 10 punktów i którzy przysłali rozwiązanie co najmniej jednego zadania z rocznika 2023, 2024 lub 2025.
W treści zadania 803 w wydrukowanej wersji numeru wrześniowego pojawił się oczywisty błąd – ładunek kuli nienaładowanej nie mógł zmaleć dwukrotnie, bo wynosił zero.
Rozwiązania zadań z numeru 9/2025
Przypominamy treść zadań:
802. Podróżny stał obok początku wagonu z numerem porządkowym \(k.\) Pociąg ruszył z miejsca, po czym okazało się, że wagon o numerze \(m\) mijał pasażera przez \(t\) sekund. Ile czasu przejeżdżał obok tego pasażera wagon o numerze \(n\)? Pociąg poruszał się ruchem jednostajnie przyspieszonym, długości wagonów są jednakowe, odległości między wagonami zaniedbywalne. Podróżny nie poruszał się względem peronu.
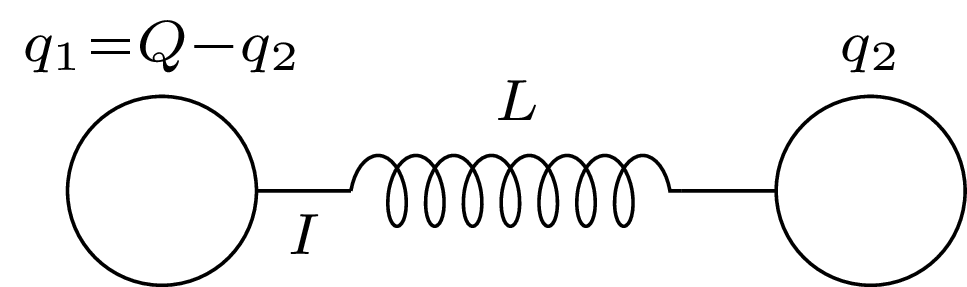
803. Dwie metalowe kule o promieniach \(R\) znajdują się w bardzo dużej odległości od siebie i połączone są cienkim przewodnikiem, w którego rozcięcie włączona jest cewka o współczynniku samoindukcji \(L.\) W chwili początkowej jedna z tych kul naładowana jest ładunkiem \(Q,\) druga nienaładowana. Po jakim czasie ładunek kuli naładowanej zmaleje dwukrotnie?
802. Oznaczmy przez \(\Delta t_i\) czas, w którym \(i\)-ty wagon przejeżdża obok podróżnego (\(i \geq k\)). Wtedy \[\tag{1} \label{1} l = {a \Delta t_k^2\over 2} \ \ \ \Rightarrow \ \ \ \Delta t_k = \sqrt{{2l\over a}},\] gdzie \(a\) jest przyspieszeniem pociągu, \(l\) długością wagonu. Zgodnie z treścią zadania \[\tag{2} \label{2} \Delta t_m = t.\] Oznaczmy przez \(t_i\) czas, w którym przejechały obok podróżnego wagony, zaczynając od numeru \(k,\) a kończąc na numerze \(i.\) Zachodzą związki: \[\tag{3} \label{3} \Delta t_i = t_i - t_{i-1}.\] W czasie \(t_i\) obok podróżnego przejechało \(i-k+1\) wagonów, zatem \[\tag{4} \label{4} (i+1-k)l = {a t_i^2\over 2} \ \ \ \Rightarrow \ \ \ t_i = \sqrt{{2l(i+1-k)\over a}},\] stąd zgodnie z (1) \[t_i = \Delta t_k \sqrt{i+1-k}, \ \ \ t_{i-1} = \Delta t_k \sqrt{i-k}.\] Uwzględniając (2) i (3): \[\begin{gathered} \Delta t_m = \Delta t_k \left( \sqrt{m+1-k} - \sqrt{m-k} \right) \\ \Rightarrow \ \ \ \Delta t_k = {t\over\sqrt{m+1-k} - \sqrt{m-k}}. \end{gathered}\] Szukany czas wynosi: \[\Delta t_n = t {\sqrt{n+1-k} - \sqrt{n-k}\over\sqrt{m+1-k} - \sqrt{m-k}}.\]
803. Oznaczmy przez \(q_2\) ładunek, który przeszedł do chwili \(t\) na kulę nienaładowaną (rys.), ładunek na pierwszej kuli wynosi w tym momencie \(q_1 = Q - q_2,\) a napięcie na cewce \[U = \phi_1 - \phi_2 = {Q-q_2\over 4 \pi \varepsilon_0 R} - {q_2\over 4 \pi \varepsilon_0 R} = {Q-2q_2\over 4 \pi \varepsilon_0 R}.\] Natężenie prądu w cewce \(I = {\mathrm d q_1\over\mathrm d t} = -{\mathrm d q_2\over\mathrm d t}\) zmienia się zgodnie z wzorem \[U = -L {\mathrm d I\over\mathrm d t} \ \ \ \Rightarrow \ \ \ {Q-2q_2\over 4 \pi \varepsilon_0 R} = L {d^2q_2\over dt^2}.\] Wprowadzając nową zmienną \(q = {Q\over 2} - q_2,\) otrzymujemy: \[{d^2q\over dt^2} + {q\over 2 \pi \varepsilon_0 R L} = 0.\] Jest to równanie oscylatora harmonicznego z warunkami początkowymi \[q(0) = {Q\over 2}, \ \ \ I(0) = 0.\] Częstość drgań wynosi \(\omega = \sqrt{{1\over 2 \pi \varepsilon_0 R L}},\) okres drgań \(T = 2 \pi \sqrt{2 \pi \varepsilon_0 R L}.\) Ładunek na pierwszej sferze \(q_1 = {Q\over 2} + q\) różni się od \(q\) tylko stałą, czyli drga z takim samym okresem. Zmaleje więc dwukrotnie po czasie \[\tau = {T\over 4} = {\pi\over 2} \sqrt{2 \pi \varepsilon_0 R L}.\] Po tym czasie ładunki na obu sferach wyrównają się do wartości \({Q\over 2},\) a napięcie między sferami spadnie do zera.