Afiliacja: Wydział Chemiczny, Politechnika Śląska w Gliwicach
O manewrze Hohmanna słyszał każdy, kto oglądał film lub czytał książkę Marsjanin. Tym właśnie sposobem odbywały się tamtejsze przeloty między Ziemią i Marsem. Manewr ten polega na przeniesieniu pojazdu kosmicznego z jednej orbity kołowej na inną z wykorzystaniem „transferowej” orbity eliptycznej. Takiej drogi nigdy nie pokonuje się, lecąc w linii prostej i hamując dopiero u celu – byłoby to marnotrawstwo energii. Jak się zaraz przekonamy, w manewrze Hohmanna czasami w ogóle nie ma potrzeby hamowania (w najprostszej wersji tylko się przyspiesza).
O manewrze Hohmanna pisał również Grzegorz Derfel w \(\Delta^8_{20}\). Ciekawemu Czytelnikowi polecamy zajrzeć do wspomnianego artykułu, który opisuje również manewr dwueliptyczny.
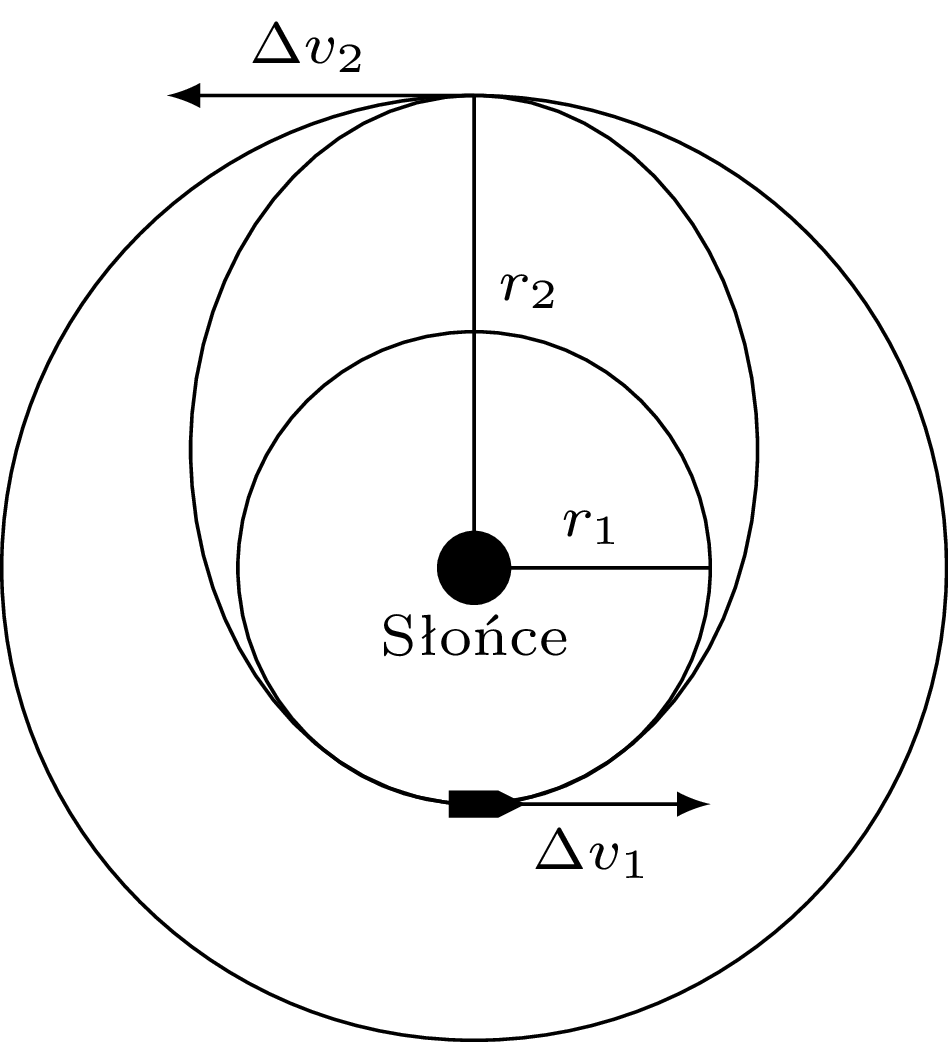
W manewrze Hohmanna wykorzystuje się dwie sekwencje włączania silników, generujące przyrosty prędkości \(\Delta v_1\) w perycentrum oraz \(\Delta v_2\) w apocentrum (rysunek obok). Aby określić wielkości skoków \(\Delta v_1\) i \(\Delta v_2,\) skorzystamy z zasady zachowania energii na orbicie: \[E = \frac{mv^2}{2} - \frac{GMm}{r}.\] Równanie to szczególnie łatwo jest analizować w apocentrum i perycentrum orbity eliptycznej – punktach największego zbliżenia do ogniska i największego oddalenia (aphelium \(r_2\) i peryhelium \(r_1\) dla ciał krążących wokół Słońca). Z zasady zachowania energii: \[\frac{mv_1^2}{2} - \frac{GMm}{r_1} = \frac{mv_2^2}{2} - \frac{GMm}{r_2}.\] Ponadto w tych punktach (na rysunku: punkty, w których zadaje się impulsy prędkości) prędkość jest prostopadła do promienia, dzięki czemu można łatwo obliczyć iloczyn wektorowy dla momentu pędu: \[mv_1 r_1 = mv_2 r_2.\] Z podstawienia powyższego równania do poprzedniego (w celu wyeliminowania \(v_1\)): \[v_2^2 \left(1 - \frac{r_2^2}{r_1^2} \right) = 2GM \left( \frac{1}{r_2} - \frac{1}{r_1} \right)\] \[\Rightarrow \ \ \ v_2^2 \cdot \frac{(r_1 - r_2)(r_1 + r_2)}{r_1^2} = 2GM \cdot \frac{r_1 - r_2}{r_1 r_2}.\] Ponieważ dla elipsy \(r_1 + r_2 = 2a\) (dwukrotna wielkość półosi wielkiej), po skróceniu \((r_1-r_2)/r_1\) mamy: \[v_2^2 = \frac{GM r_1}{a~r_2} = \frac{GM(2a - r_2)}{a~r_2} = \frac{2GM}{r_2} - \frac{GM}{a}.\] Korzystając z powyższego równania, możemy wyznaczyć wartość całkowitej energii ciała na orbicie o danej długości wielkiej półosi: \[E = \frac{mv_{2}^2}{2} - \frac{GMm}{r_2} = \frac{GMm}{r_2} - \frac{GMm}{2a} - \frac{GMm}{r_2} = -\frac{GMm}{2a}.\] Podstawiając tę wartość do zasady zachowania energii przytoczonej na początku i skracając masę, uzyskujemy tzw. równanie vis-viva (w języku polskim tłumaczone niekiedy jako „całka siły żywej”): \[v^2 = GM \left( \frac{2}{r} - \frac{1}{a} \right). \tag{$*$}\] Za pomocą tego równania można łatwo znaleźć przyrosty prędkości potrzebne do zmiany orbity. Jeżeli początkowo jesteśmy na orbicie kołowej, to \(a = r = r_1.\) Potem przechodzimy na orbitę eliptyczną, gdzie \(a = (r_1 + r_2)/2.\) W końcu docieramy do perycentrum elipsy (ew. apocentrum, jeśli planujemy obniżyć orbitę), gdzie znowu promień równy jest półosi: \(a = r = r_2.\)
Transfer z orbity ziemskiej na marsjańską
Policzmy przykładowe przyrosty prędkości podczas transferu na orbitę Marsa (orbita kołowa o promieniu \(r_2 = 229\) mln km) z orbity ziemskiej o promieniu \(r_1 = 150\) mln km). Orbity liczone są wokół Słońca, więc \(GM_\odot = 1{,}3 \cdot 10^{11} \, \text{km}^3/\text{s}^2.\) Z równania \((*)\) mamy: \[\begin{aligned} v_1 & = \sqrt{ \frac{1{,}3 \cdot 10^{11}}{10^6} \cdot \frac{1}{150} } = 29{,}4 \, \text{km/s}, \\ v_{12}(r_1) & = \sqrt{ \frac{1{,}3 \cdot 10^{11}}{10^6} \left( \frac{2}{150} - \frac{2}{150 + 229} \right)} = 32{,}4 \, \text{km/s} \ \ \ \Rightarrow \Delta v_1 = 3{,}0 \, \text{km/s}, \\ v_{12}(r_2) & = \sqrt{ \frac{1{,}3 \cdot 10^{11}}{10^6} \left( \frac{2}{229} - \frac{2}{150 + 229} \right)} = 21{,}2 \, \text{km/s}, \\ v_2 & = \sqrt{ \frac{1{,}3 \cdot 10^{11}}{10^6} \cdot \frac{1}{229} } = 23{,}8 \, \text{km/s} \ \ \ \Rightarrow \Delta v_2 = 2{,}6 \, \text{km/s}, \end{aligned}\] przy czym \(v_{12}\) to prędkość na orbicie eliptycznej łączącej orbity Ziemi i Marsa.
W praktyce transfer rzadko jest wykonywany z orbity ziemskiej poza polem grawitacyjnym Ziemi i rzadko wejście na orbitę marsjańską zachodzi daleko od Marsa. Rozpoczynając misję na niskiej orbicie okołoziemskiej (Low Earth Orbit – LEO), \(v_\text{LEO} = 7{,}9\) km/s, musielibyśmy się po pierwsze wyzwolić z pola grawitacyjnego Ziemi (\(M = 5{,}97 \cdot 10^{24}\) kg, \(r_\text{LEO}=6371\) km), a po drugie nadać sondzie prędkość transferową względem Ziemi. Uwzględniając, że dysponujemy już częścią energii kinetycznej, związanej z ruchem po orbicie LEO, możemy rozpisać zachowanie energii: \[\begin{gathered} \Delta E = \frac{m(v_\text{LEO} + \Delta v)^2}{2} - \frac{mv_\text{LEO}^2}{2} = \frac{GMm}{r_\text{LEO}} - \frac{mv_\text{LEO}^2}{2} + \frac{m(v_{12} - v_1)^2}{2}, \\ v_\text{LEO} + \Delta v = 11{,}5 \, \text{km/s} \ \ \ \Rightarrow \Delta v = 3{,}6 \, \text{km/s}. \end{gathered}\] Powyższą zależność energetyczną można wyrazić w bardziej typowy sposób, mianowicie: aby uzyskać prędkość \(v_\infty\) po uwolnieniu się z pola grawitacyjnego planety, przy założeniu prędkości ucieczki \(v_{\textup{II}} = \sqrt{2GM/R},\) trzeba nadać pojazdowi kosmicznemu prędkość: \[v = \sqrt{v_{\textup{II}}^2 + v_\infty^2}. \tag{$**$}\] Prędkości mierzymy tu względem planety – energia najpierw jest wykorzystywana na pokonanie pola grawitacyjnego (w wielkości \({v_{\textup{II}}}^2\)), a pozostała część pozostaje zachowana w postaci energii kinetycznej. Jest to ten sam wzór, który mamy wyżej dla \(\Delta E.\) Zaniedbujemy tutaj efekty oddziaływania ze Słońcem i w tym przybliżeniu zajmujemy się orbitą hiperboliczną (w odległościach pojedynczych milionów kilometrów od planety możmy zaniedbać zakrzywienie trajektorii związane z oddziaływaniem ze Słońcem, co upraszcza analizę!).
Załóżmy teraz, że docieramy w okolice Marsa i zastanawiamy się, jak skorygować prędkość, aby zostać przez niego przechwyconym i wejść na jego orbitę. Skorzystamy z równania \((**)\) łączącego prędkość orbitalną z prędkością ucieczki i prędkością \(v_\infty,\) tym razem dla danej prędkości zbliżenia do planety, \(v_\infty = v_2 - v_{12}(r_2) = 2{,}7\) km/s. Prędkość ucieczki z Marsa, którego masa wynosi \(M_{mars} = 6{,}39 \cdot 10^{23}\) kg, a promień \(r_{mars} = 3390\) km, to: \[v_{\textup{II},mars } = \sqrt{ \frac{2GM_{mars} }{r_{mars} } } = 5{,}0 \, \text{km/s}.\] W efekcie, po przechwyceniu przez grawitację planety, przy założeniu maksymalnego zbliżenia aż do odległości \(r_{mars} ,\) prędkość na orbicie hiperbolicznej (w przybliżeniu zaniedbującym oddziaływanie ze Słońcem) wyniesie: \[v = \sqrt{5{,}0^2 + 2{,}7^2} = 5{,}7 \, \text{km/s}.{}\] Odejmując od tego wyniku prędkość orbitalną Marsa (\(3{,}6\) km/s), uzyskujemy wartość drugiego skoku prędkości: \[\Delta v_2 = v - v_{\textup{I},mars } = 2{,}1 \, \text{km/s}.\] W konsekwencji całkowity „budżet delta-v” dla wyprawy na Marsa wynosi: \[3{,}6 + 2{,}1 = 5{,}7 \, \text{km/s}.\]
Jako pożyteczne ćwiczenie dla Czytelników proponujemy obliczenie przyrostu \(\Delta v_2\) z wykorzystaniem orbit hiperbolicznych, omówionych w \(\Delta^{10}_{25}\). Wystarczy wyznaczyć parametr zderzenia dla minimalnego zbliżenia do samej powierzchni planety, a następnie wyznaczyć prędkość mijania planety z zachowania momentu pędu.
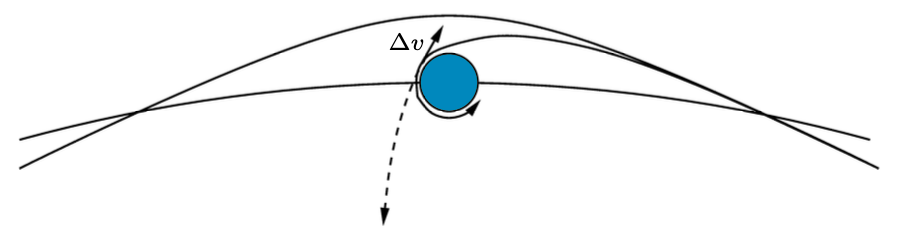
Aby bliżej uświadomić sobie związek modelowania wejścia na orbitę z orbitami hiperbolicznymi, warto spojrzeć na powyższy rysunek, gdzie Mars orbituje po okręgu, a kołową orbitę przecina elipsa Hohmanna. Pod wpływem grawitacji Marsa w pobliżu planety elipsa (tak naprawdę w tej skali i elipsa Hohmanna, i koło orbity Marsa wyglądają jak linia prosta!) ugina się i przypomina lokalnie hiperbolę. Dzięki impulsowi prędkości z hiperboli wchodzimy na orbitę kołową wokół Marsa.
Zamiast takich obliczeń łatwiej jest wykorzystać tzw. mapy delta-v – tabele skoków prędkości niezbędnych do dotarcia z punktu startowego do docelowego. Na takiej mapie rozpoczynamy sumowanie czynników, np. od orbity LEO na Ziemi, a kończymy na LMO nad Marsem.
Strefy oddziaływań planet
Mapy delta-v są dość czytelne, ale wątpliwości może wzbudzić pojęcie „przechwycenia” czy „wejścia w sferę oddziaływania” planety. Sfera oddziaływania definiowana jest jako miejsce, gdzie pojazd kosmiczny – pomiędzy planetą a Słońcem (czy ogólniej: pomiędzy mniejszym ciałem niebieskim a dominującym ciałem niebieskim) – odczuwa zerową siłę wypadkową grawitacji oraz odśrodkową: \[\frac{GMm}{R^2} + m\omega^2(r_1 - R) - \frac{GM_\odot m}{(r_1 - R)^2} = 0,\] \(r_1\) oznacza tu promień orbity planety, a \(R\) to odległość strefy oddziaływania od planety.
Ponieważ orbitalna prędkość kątowa planety wynika z równowagi siły odśrodkowej z przyciąganiem Słońca: \[\omega^2 r_1 = \frac{GM_\odot}{r_1^2}.\] Jednocześnie różnica dwóch ostatnich członów względem punktu równowagi w \(r_1\) jest mała, i aby uprościć rachunki, można skorzystać z następującego przybliżenia: \[\frac{1}{(r_1 - R)^2} \approx \frac{1}{r_1^2} -R \left[ \frac{d}{d r_1} \left( \frac{% 1}{r_1^2} \right) \right] = \frac{1}{r_1^2} + 2 \frac{R}{r_1^3}.\] Mamy zatem: \[\frac{GMm}{R^2} + \frac{GM_\odot m}{r_1^2} -\frac{GM_\odot m}{r_1^3}R = \frac{GM_\odot m}{r_1^2} + 2\frac{GM_\odot m}{r_1^3}R.\] I stąd możemy wyznaczyć promień sfery oddziaływania dla Ziemi: \[R = r_1 \sqrt[3]{\frac{M}{3M_\odot}} = 1{,}5 \, \text{mln km}.\]
Literatura
RR Bate, DD Mueller, JE White, Fundamentals of Astrodynamics, Dover, 1971.
W. Hohmann, Attainability of Celestial Bodies, NASA, 1925. (równania (41), (45), rys. 25)
JE Marsden, SD Ross, New Methods in Celestial Mechanics and Mission Design, Bulletin of the AMS, vol. 43, s. 43, 2005.
RD Johnson, Ch Holbrow, Space Settlements, NASA, 1977.
Kalkulator trajektorii transferowych:
https://trajbrowser.arc.nasa.gov/Mapa „delta-v”: https://upload.wikimedia.org/wikipedia/commons/9/93/Solar_system_delta_v_map.svg