Afiliacja: Instytut Fizyki Teoretycznej, Wydział Fizyki Uniwersytetu Warszawskiego
Spontaniczny przepływ ciepła zachodzi od ciała o wyższej temperaturze do ciała o niższej temperaturze. Jest to jedno ze sformułowań drugiej zasady termodynamiki według Clausiusa. Nie można uzyskać pracy w procesie cyklicznym, pobierając energię jedynie z jednego rezerwuaru. Jest to sformułowanie tej samej zasady termodynamiki, ale według Kelvina. Oba sformułowania są równoważne, patrz \(\Delta^3_{20}\). Można je też zapisać matematycznie: Istnieje funkcja stanu \(S\) zwana entropią, patrz \(\Delta_{19}^4\), która w układzie izolowanym, w którym zachodzi proces termodynamiczny, nigdy nie maleje: \(\Delta S\geq 0.\) Gdy zachodzi równość, to taki proces, z definicji, nazywamy odwracalnym.
Pozorna sprzeczność drugiej zasady termodynamiki z odwracalnymi w czasie prawami dynamiki Newtona w mechanice klasycznej pobudzała wyobraźnię uczonych, patrz \(\Delta_{19}^1\). Już w 1867 roku James Maxwell zaproponował eksperyment myślowy mający obalić bezwzględną słuszność drugiej zasady termodynamiki. Rozwiązanie tego paradoksu zajęło 115 lat, a temat ten jest nadal żywy i interesujący. Doczekał się też weryfikacji doświadczalnej.
James Clerk Maxwell (1831–1879) – szkocki fizyk i matematyk, laureat Medalu Rumforda (1860).
Maxwell
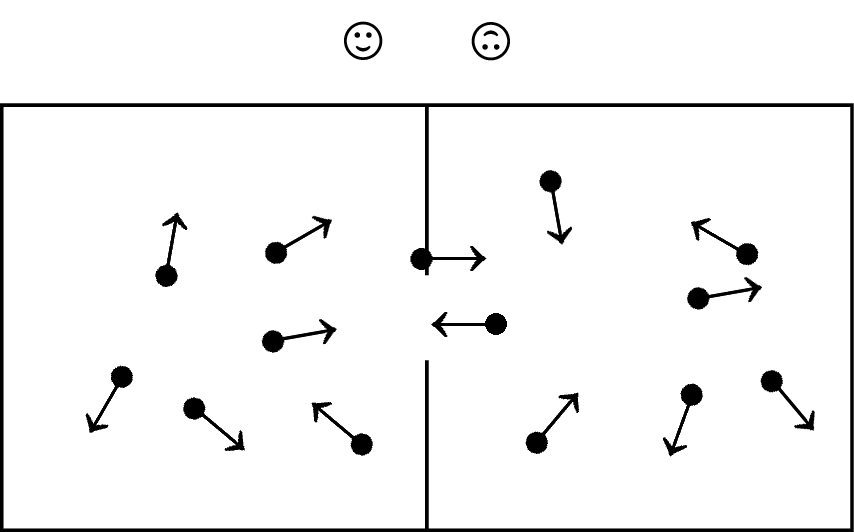
W eksperymencie myślowym James Maxwell zaproponował, aby podzielić przegrodą na dwie części pudło z gazem znajdującym się w równowadze termodynamicznej. Temperatury gazu w obu połówkach są identyczne, średnia energia kinetyczna cząsteczek również. Oznacza to jednocześnie, że w obu połówkach są cząsteczki zarówno szybsze, jak i wolniejsze . Maxwell wprowadził niewielki otwór w przegrodzie, otwieranie i zamykanie którego nie wymaga pracy. I na koniec wprowadził super-stworka, który ma mierzyć prędkości cząsteczek, i jeśli cząsteczka lecąca w stronę otworu z prawej strony ma prędkość większą od średniej prędkości, otwiera przegrodę i pozwala jej polecieć na lewą stronę. Odwrotnie, z lewej strony przepuszcza na prawo jedynie te cząsteczki, których prędkości są mniejsze od średniej. W efekcie po upływie pewnego czasu lewa strona ma więcej szybszych cząsteczek niż prawa i jej temperatura jest wyższa niż temperatura prawej strony. Teraz wystarczy podłączyć silnik cieplny pomiędzy tak stworzonymi rezerwuarami i uzyskać pracę. Powstało perpetuum mobile drugiego rodzaju. Oczywiście jest to sprzeczne z drugą zasadą termodynamiki w sformułowaniu Clausiusa. Ciepło nie może przepływać bez początkowej różnicy temperatur. Parę lat później, w 1874 roku, Kelvin nazwał tego wyimaginowanego stworka demonem Maxwella. Choć w literaturze demon Maxwella był przedstawiany jako ktoś obdarzony inteligencją, to w istocie jest to odpowiednio zaprojektowane urządzenie pomiarowe.
Rys. 1. Schemat ilustrujący działanie demona Maxwella. Przegroda otwiera się tak, aby przepuścić szybkie cząstki lecące z prawego pudła do lewego i wolne cząstki lecące z lewego pudła do prawego. Po upływie pewnego czasu temperatury w obu pudłach będą różne. Lewe pudło będzie miało wyższą temperaturę, a prawe niższą.
Demon (stgr. \(\delta\alpha\iota\mu\omega\nu,\) daimon, nadprzyrodzona potęga, dola; łac. daemon) – istota występująca w wielu wierzeniach ludowych, mitologiach i religiach, która zajmuje pozycję pośrednią między bogami a ludźmi, między sferą ziemsko-ludzką, materialną a sferą boską, czysto duchową; istota o cechach na wpół ludzkich, na wpół boskich; najczęściej nieprzyjazny człowiekowi duch, związany pierwotnie z pojęciem nieczystości sakralnej. (Wikipedia)
Szilárd
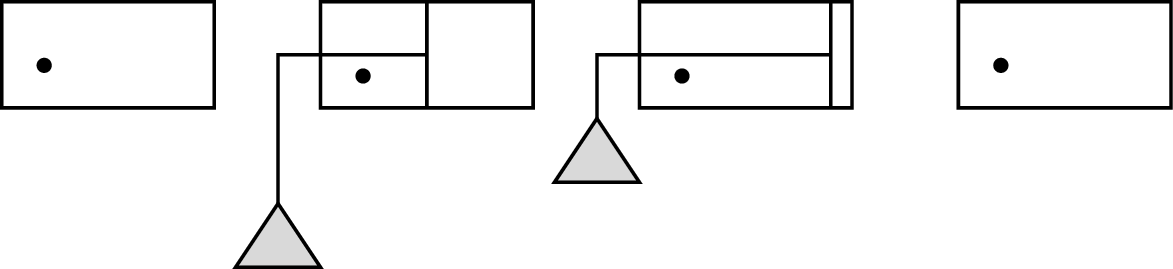
Mimo gorących dyskusji żaden postęp w zrozumieniu problemu (paradoksu) demona Maxwella nie nastąpił – aż do 1929 roku. Wtedy to Leó Szilárd (czytaj Silard) zaproponował uproszczoną wersję rozumowania Maxwella, znaną obecnie pod nazwą silnika Szilárda. W swoim eksperymencie myślowym rozważył on pojemnik o objętości \(V\) z jedną cząsteczką (lub atomem) spełniającą równanie stanu gazu doskonałego \(pV=k_BT\) (\(k_B\) jest to stała Boltzmanna). W wyniku zderzeń ze ściankami cząstka może wymieniać energię z otoczeniem i po każdym takim zderzeniu jej energia kinetyczna wraca do wartości odpowiadającej temperaturze otoczenia \(T.\) Demon umieszcza dokładnie po środku ruchomą nieważką przegrodę i sprawdza, po której stronie znajduje się cząsteczka. Po tej stronie, po której jest cząsteczka, umieszcza nieważką nić przewiniętą przez nieważki bloczek, a na końcu nici zawieszona jest masa. Wszystkie czynności zrobione przez demona nie wymagały wykonania pracy. Teraz, gdy cząsteczka uderzy (wielokrotnie) w przegrodę, spowoduje jego kwazistatyczne (odwracalne) przemieszczenie się i podniesienie masy na pewną wysokość. Tłok wykonał pracę, podniósł masę, a wykonana praca jest zgromadzona w postaci energii potencjalnej grawitacji. Wykonana praca nad układem przy maksymalnym przesunięciu się tłoka wynosi \[W=-\int_{V/2}^Vp(V)dV = - k_BT \ln 2<0,\] czyli układ wykonał pracę równą \(\bar{W}=k_BT\ln 2.\) Mamy sprzeczność z drugą zasadą termodynamiki w sformułowaniu Kelvina. Dla utrzymania stałej temperatury (proces izotermiczny) układ pobrał z rezerwuaru ciepło w ilości \(Q=k_BT \ln 2,\) które zostało w całości zamienione na pracę. Entropia rezerwuaru zmalała o \(\Delta S=Q/T=k_B\ln 2.\) Szilárd i jego następcy błędnie uważali (bez podania dowodu), że proces pomiaru położenia cząsteczki musi produkować entropię nie mniejszą niż \(k_B\ln 2,\) aby uratować drugą zasadę termodynamiki.
Leó Szilárd (1898–1964) – węgiersko-amerykański fizyk i biolog molekularny.
Rys. 2. Schemat ilustrujący eksperyment myślowy opisujący działanie silnika Szilárda. Po lewej stronie ciśnienie gazu \(p\) wytwarzane przez jedną cząsteczkę poruszającą się chaotycznie i uderzającą w ścianki, po prawej stronie próżnia. Ponieważ energia wewnętrzna gazu doskonałego się nie zmieniła, \(U=\frac{3}{2}k_BT,\) gaz pobrał ciepło z otoczenia, aby utrzymać stałą temperaturę \(T\) i wykonać pracę \(\bar{W},\) co jest zgodne z pierwszą zasadą termodynamiki \(\Delta U=Q+\bar{W}.\)
Landauer
Rolf Wilhelm (William) Landauer (1927–1999) – amerykański fizyk, znany z tzw. zasady Landauera. Zajmował się informatyką teoretyczną.
Najważniejszy krok w kierunku wyjaśnienia paradoksu demona Maxwella dokonał się w 1961 roku wraz z przełomową pracą Rolfa Landauera. Tematem pracy Landauera nie był jednak paradoks demona Maxwella per se, lecz problem przetwarzania logicznego, zapisywania i kasowania informacji. Sama matematyczna koncepcja informacji logicznej powstała w 1948 roku. Claude Shannon powiązał informację z prawdopodobieństwem otrzymania danego przekazu \(p_i.\) Im mniejsze jest to prawdopodobieństwo, tym większa musi być ilość informacji zawarta w tym przekazie. Wiadomość, której treść jest wcześniej znana, \(p_i=1,\) nie zawiera żadnej informacji. Dla danego rozkładu prawdopodobieństwa \(\{p_i\}\) Shannon wprowadził średnią informację \({H=-\sum_i p_i \log_2 p_i} ,\) znaną obecnie jako entropia informacji. Logarytm przy podstawie \(2\) nawiązuje do układu binarnego i bitu informacji, stanu logicznego \(0\) lub \(1.\) Podobno na pomysł, aby nazwać wielkość \(H\) entropią, wpadł John von Neumann, w konwersacji z Shannonem stwierdził, że i tak nikt nie rozumie, czym jest entropia, więc ta nazwa będzie dobra.
Landauer podzielił logiczne procesy przetwarzania informacji na odwracalne i nieodwracalne. Przykładem operacji odwracalnej jest operacja jednobitowa NOT lub dwubitowa CNOT. Jak widać z tabelki działania, znajomość bitu (bitów) końcowego pozwala jednoznacznie określić bit (bity) początkowy. Operacje odwracalne są iniekcją, odwzorowaniem jeden na jeden. Są też operacje nieodwracalne, na przykład operacja OR. Na podstawie znajomości bitu końcowego nie umiemy ustalić, jakie były bity początkowe.
\(p\) \(\lnot p\) 0 1 1 0
Odwracalna operacja logiczna NOT
\(p\) \(q\) \(p'\) \(q'\) 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 0
Odwracalna operacja logiczna CNOT
\(p\) \(q\) \(p \lor q\) 0 0 0 0 1 1 1 0 1 1 1 1
Nieodwracalna operacja logiczna OR
Ponadto Landauer powiązał proces przetwarzania informacji z procesem fizycznym. Nośnikiem informacji zawsze jest jakiś układ fizyczny, a przetwarzaniu informacji musi towarzyszyć zjawisko fizyczne, zgodne z prawami fizyki. W szczególności zgodne z prawami termodynamiki. Na przykład stanowi logicznemu \(0\) odpowiada cząsteczka znajdująca się w lewej połówce pudełka, w stanie \(L,\) a stanowi logicznemu \(1\) odpowiada cząsteczka w prawej połowie, w stanie \(R.\) Oczywiście możliwych realizacji stanu jednego bitu jest bardzo wiele. Nośnikiem może być polaryzacja fotonu, magnetyzacja domeny magnetycznej, spin elektronu, stan ładunkowy bramki MOSFET i wiele innych możliwości.
Odwracalnym procesom logicznym odpowiadają w przyrodzie odwracalne procesy fizyczne, niezmieniające całkowitej entropii układu. Na przykład proces zapisywania czy zapamiętywania informacji jest procesem odwracalnym i polega na kopiowaniu jeden do jednego stanu pierwszego układu na drugi. Nie ma tutaj jakiejś minimalnej pracy, która byłaby potrzebna, aby skopiować stan jednego bitu na stan drugiego.
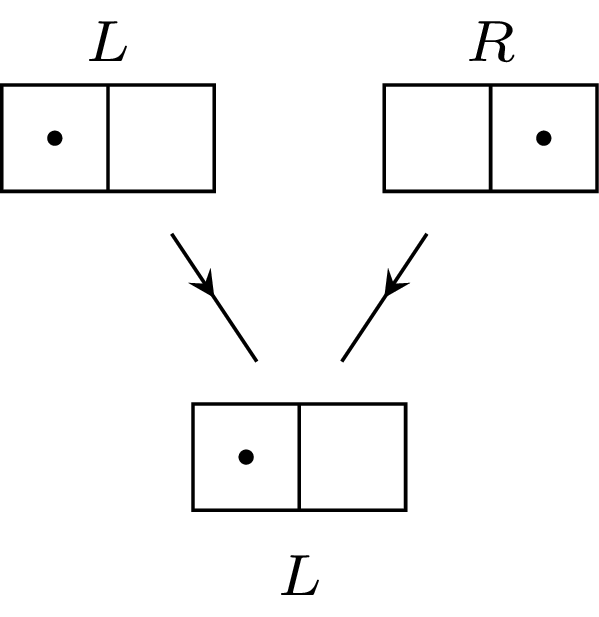
Najważniejszym spostrzeżeniem Landauera jest jednak obserwacja, że proces wymazywania pamięci jest nieodwracalny i tym samym odpowiadający mu proces fizyczny jest też nieodwracalny, generujący ciepło czy dyssypację energii i zwiększający całkowitą entropię układu. Faktycznie, jeśli umówimy się, że standardowym stanem odniesienia, nieniosącym informacji, jest stan, w którym cząsteczka jest w lewej połowie, to zarówno stan logiczny \(0,\) jak i \(1,\) którym odpowiadało położenie cząsteczki \(L\) i \(R,\) jest przekształcany w stan \(L,\) czyli logiczne \(0.\) Po wymazaniu pamięci nie możemy już sprawdzić, jaki był stan początkowy bitu. Taki proces jest nieodwracalny i musi generować ciepło.
Rys. 3. Nieodwracalna operacja wymazania (skasowania) pamięci. Stany \(L\) i \(R\) są mapowane na ten sam stan odniesienia, zgodnie z naszą umową \(L.\) Znając tylko stan końcowy, nie wiemy, w jakim stanie początkowym był układ. Tej operacji nie można odwrócić.
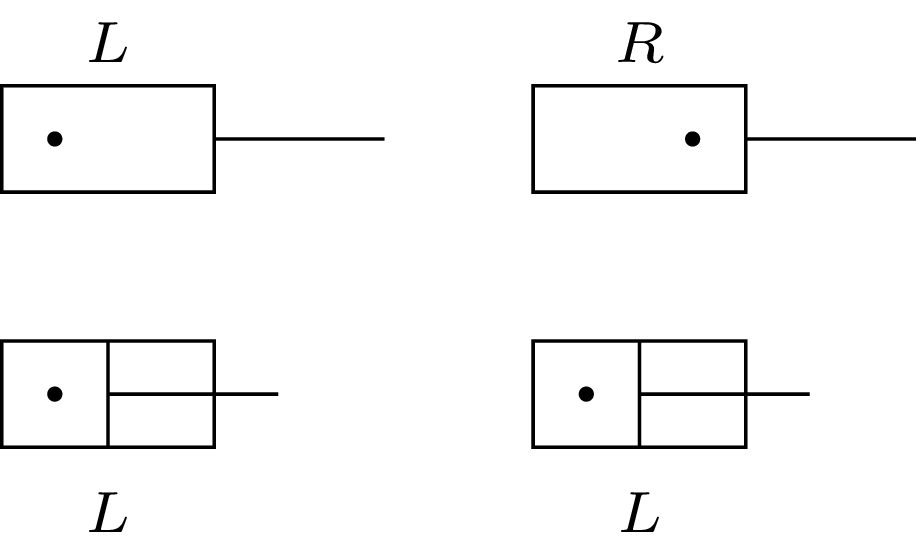
Pracę potrzebną do wymazania jednego bitu pamięci znajdziemy, biorąc pudełko o objętości \(V\) z jedną cząsteczką pozostajacą w kontakcie z rezerwuarem o temperaturze \(T,\) znajdującą się z lewej, \(L,\) lub prawej, \(R,\) strony. Teraz od prawej strony przesuwamy bardzo powoli i bez tarcia (kwazistatycznie) tłok, redukując objętość z \(V\) do \(V/2.\) Niezależnie od tego, w jakim stanie początkowym była cząsteczka, po tej operacji znajduje się ona w standardowym stanie odniesienia \(L.\) Wykonana praca nad układem wynosi \(W=k_BT\ln 2.\) Praca ta przekazana jest do otoczenia w postaci ciepła \(Q.\)
Rys. 4. Fizyczna realizacja wymazania pamięci
Prawo Landauera stwierdza, że minimalna praca potrzebna do wymazania jednego bitu informacji z pamięci w danej temperaturze \(T\) wynosi \(k_BT\ln 2.\) O ile uczenie się, zapamiętywanie, teoretycznie nie wymaga pracy, to niestety zapominanie zawsze związane jest z pewną pracą. Dość przewrotna konkluzja.
Bennett
Wróćmy do drugiej zasady termodynamiki i demona Maxwella. W 1982 roku Charles Bennett powiązał odkrycia Landauera z ponadstuletnim paradoksem Maxwella. Nawiasem mówiąc, do podobnych wniosków doszedł już w 1970 roku Oliver Penrose. Aby demon Maxwella czy silnik Szilárda działały w sposób cykliczny, pamięć demona, w której zapisany był stan cząsteczki, musi być wymazana (zresetowana). Jedynie wtedy operacja pomiaru stanu cząsteczki mogła zostać powtórzona. Tak więc nie pomiar stanu cząsteczki, nie otwieranie przegrody lub mocowanie nitki i bloczka, jak błędnie zakładali Szilárd i inni, lecz proces kasowania pamięci prowadzi do dyssypacji energii i sprawia, że druga zasada termodynamiki jest nadal prawdziwa. Egzorcyzmy nad demonem Maxwella zostały dopełnione.
Charles H. Bennett (ur. 1943) – amerykański fizyk, filozof.
Największym chyba zaskoczeniem jest jednak powiązanie dwóch z pozoru zupełnie różnych światów, teorii informacji i termodynamiki. Z punktu widzenia teorii informacji bit w stanie \(0\) lub \(1\) ma entropię informacji równą \(\log_2 2=1,\) gdyż są dwie możliwości z tym samym prawdopodobieństwem \(1/2.\) Stan standardowy bez informacji \(0\) ma entropię \(\log_2 1=0,\) gdyż prawdopodobieństwo wystąpienia tego stanu wynosi jeden. Mamy więc zmianę entropii informacyjnej o jeden w nieodwracalnym logicznie procesie kasowania pamięci.
Zakładając teraz, za Landauerem, że procesom logicznym odpowiadają procesy fizyczne, możemy przyrównać entropię informacji i entropię termodynamiczną: \[S=c H,\] gdzie \(c=k_B /\log_2 e\) jest związane ze zmianą podstawy logarytmu z \(2\) na \(e\) oraz z tym, że entropia termodynamiczna ma wymiar \(J/K.\) Tym samym zmiana entropii wynosi \(\Delta S=k_B\ln 2\) i ilość energii oddanej jako ciepło \({Q=T\Delta S=k_BT\ln 2}\) wynosi dokładnie tyle co poprzednio.
Postscriptum
Literatura
1. R. Landauer, Information is physical, „Physics Today”, May 1991, str. 23–29.
2. Ch. Bennett, Notes on Landauer’s principle, reversible computation, and Maxwell’s demon, „Studies in History and Philosophy of Modern Physics” 34, (2003), str.501–510.
3. E. Lutz, S. Ciliberto, Information: From Maxwell’s demon to Landauer’s eraser, „Physics Today”, September 2015, str. 30–35.
4. K. Robertson, The demons haunting, „Physics Today”, November 2021, str. 44–50.
5. R. Feynman, Przetwarzanie informacji, PWN, 2022.
Po rozwiązaniu eksperymentu myślowego naukowcy rozpoczęli prawdziwe eksperymenty z demonem Maxwella w laboratoriach. Na przełomie XX i XXI wieku stały się możliwe eksperymenty, w których manipuluje się pojedynczymi atomami, elektronami czy fotonami. To otworzyło drogę do skonstruowania demona Maxwella. Na przykład w 2007 roku naukowcy wykorzystali bramkę zasilaną światłem, aby zademonstrować działanie demona Maxwella. W 2010 roku inny zespół opracował sposób wykorzystania energii wytworzonej przez informacje demona do wprawienia kulki w ruch, w górę, a w 2016 roku naukowcy zastosowali koncepcję demona Maxwella do dwóch komór zawierających nie gaz, ale światło. Wykorzystano też aparat mechaniki kwantowej do sformułowania termodynamiki kwantowej i badania kwantowego odpowiednika demona Maxwella.
Jak widać, problem zamiany energii w pracę, pochodzący jeszcze z XIX wieku, jest nadal żywy i aktualny.