Wielomian \(x^3 + px^2 + qx + r\) ma trzy pierwiastki w przedziale \((0,2).\) Udowodnić, że \[-2<p + q + r<0.\]
Dana jest liczba całkowita dodatnia \(n\) taka, że \[\gcd(n, n+1)<\gcd(n, n+2)<\ldots < \gcd(n, n+35).\] Udowodnić, że \[\gcd(n, n+35)<\gcd(n, n+36).\]
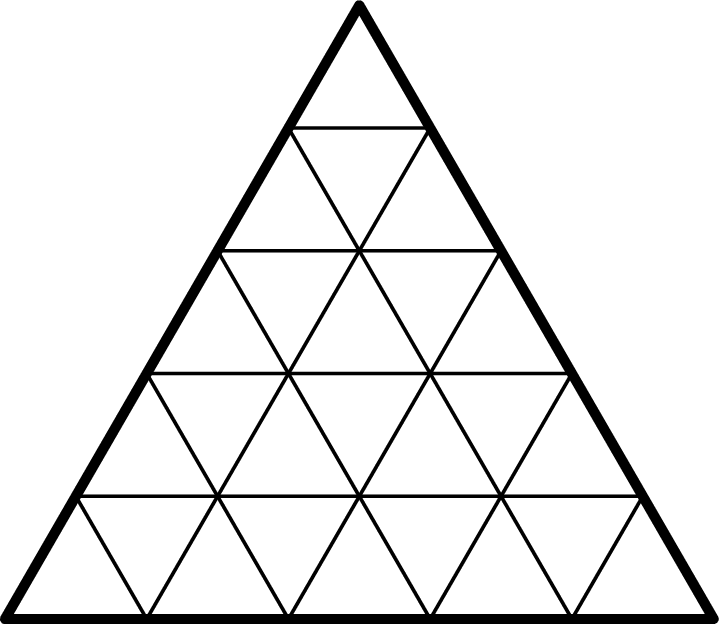
Tabliczka czekolady w kształcie trójkąta równobocznego o boku długości \(p\) składa się z \(p^2\) kostek, czyli kawałków w kształcie trójkąta równobocznego o bokach długości \(1,\) równoległych do boków tabliczki czekolady. Dwóch graczy na zmianę może odłamać kawałek w kształcie trójkąta (łamiąc wzdłuż jednej z linii podziału czekolady na kostki). Gracz, który nie ma ruchu lub zostawi przeciwnikowi dokładnie jedną kostkę, przegrywa. Załóżmy, że \(p\) jest liczbą pierwszą. Który z graczy ma zwycięską strategię?
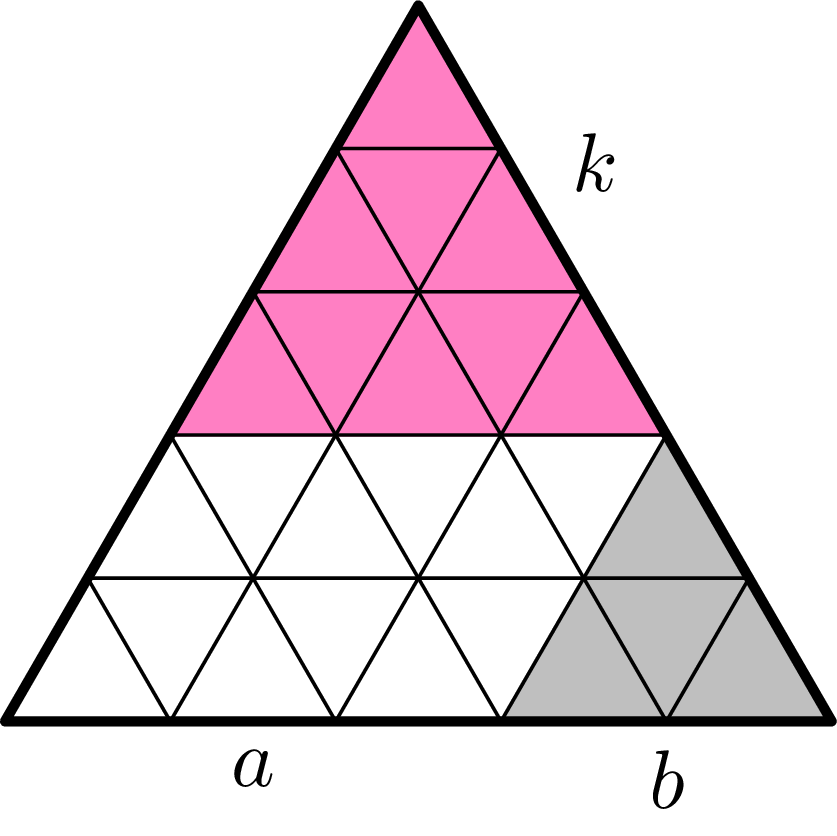
Pierwszego gracza oznaczmy przez \(A,\) drugiego przez \(B.\) Opiszemy teraz strategię wygrywającą dla \(B.\) Przypuśćmy, że \(A\) zjada kostkę wymiaru \(k,\) pozostawiając trapez o bokach \(k,\) \(p-k,\) \(p,\) \(p-k.\) Niech \(a=\max (k, p-k),\) \(b=\min (k, p-k).\) Ponieważ \(\gcd(a,b)=\gcd(k, p-k)=1,\) więc \(a\neq b.\) Gracz \(B\) zjada zatem trójkąt o boku \(p-k,\) pozostawiając równoległobok o wymiarach \(a\) na \(b.\) Teraz rozpatrzmy dwa przypadki:
Załóżmy, że \(A\) zjada kawałek o wymiarach mniejszych niż \(b,\) wtedy \(B\) zjada kawałek symetryczny względem środka równoległoboku i wygrywa, gdyż \(A\) w tym momencie nie ma ruchu.
Jeśli zaś \(A\) zjada trójkąt o boku \(b,\) pozostawia trapez o bokach \(a-b,\) \(b,\) \(a,\) \(b,\) gdzie znowu \(\gcd(a-b,b) = \gcd(a,b) = 1.\) Gracz \(B,\) kontynuując swoją strategię, doprowadzi do sytuacji, w której \(a = b = 1\) (gdyż \(\gcd(a,b) = 1\)), co oznacza, że po ruchu \(A\) pozostaje ostatnia kostka, stąd \(B\) wygrywa.
Pytanie: Który z graczy ma wygrywającą strategię, jeśli bok czekolady jest liczbą złożoną?
Cząstka jest wyrzucona pionowo w górę z powierzchni Ziemi z prędkością wystarczającą, aby osiągnąć nieskończoną wysokość (zaniedbując opór powietrza). Udowodnij, że czas potrzebny do osiągnięcia wysokości \(h\) dany jest wzorem:
\[t = \frac{1}{3}{\sqrt{\frac{2R}{g}}} \left[ \left(1 + \frac{h}{R} \right)^{3/2} - 1 \right],\]
\(R\) to promień Ziemi, a \(g\) przyspieszenie grawitacyjne na jej powierzchni.
[Źródło: Newtonian Dynamics, Richard Fitzpatrick.]
Zamiast tego dzielimy ruch na nieskończenie małe odcinki drogi \(dr\), w których prędkość \(v(r)\) można uznać za prawie stałą. Dla każdego takiego odcinka czas przebycia wynosi właśnie \(dt = \frac{dr}{v(r)}\). Sumując te małe czasy dla wszystkich odcinków od \(r = R\) do \(r = R + h\), otrzymujemy całkowity czas ruchu jako właśnie całkę: \[\begin{aligned} t & = \int_{R}^{R+h} \frac{dr}{v(r)} = \int_{R}^{R+h} \frac{dr}{\sqrt{\frac{2gR^2}{r}}} = \frac{1}{\sqrt{2gR^2}} \int_{R}^{R+h} \sqrt{r} \, dr \\ & = \frac{1}{\sqrt{2gR^2}} \cdot \left[ \frac{2}{3} r^{3/2} \right]_{R}^{R+h} = \frac{2}{3\sqrt{2gR^2}} \left( (R + h)^{3/2} - R^{3/2} \right) \end{aligned}\] Zauważmy, że \((R + h)^{3/2} = R^{3/2} \left(1 + \frac{h}{R} \right)^{3/2},\) więc: \[t = \frac{1}{3}{\sqrt{\frac{2R}{g}}} \left[ \left(1 + \frac{h}{R} \right)^{3/2} - 1 \right].\]
Hydroniusz Kranowski postanowił wykonać w ogrodzie ciekawe doświadczenie. Zamierzał zmierzyć przepływ wody z kranu ogrodowego z wykorzystaniem jedynie linijki.
Ustalił, że średnica przy miejscu wypływu ma
\(d_1 = 10\,\mathrm{mm}\), a w odległości \(\Delta L = 0{,}5\,\mathrm{m}\) od tego miejsca średnica strumienia wynosi \(d_2 = 6\,\mathrm{mm}\). Pomóż Hydroniuszowi obliczyć natężenie przepływu wody \(Q\) w jednostkach \(\mathrm{m}^3/\mathrm{s}\).
[Zadanie oraz grafika zaczerpnięte z książki: 100 prostych doświadczeń z wodą i powietrzem Ryszarda Błażejewskiego.]
\(v_{2}\) \(d_{1}\) \(d_{2}\) \(\Delta L\) \(v_{1}\)
Schemat strumienia wody wypływającego z kranu
Choć dzisiaj równanie \(\eqref{eq:przeplyw}\) wydaje się oczywiste, zostało ono sformułowane dopiero w XVII wieku.
Dla cieczy idealnej (czyli takiej, w której można pominąć straty energii) równanie Bernoulliego zastosowane do przepływu między punktami 1-1 i 2-2 przyjmuje postać: \[\frac{v_1^2}{2g} + \frac{p_1}{\varrho_w g} + z_1 = \frac{v_2^2}{2g} + \frac{p_2}{\varrho_w g} + z_2.\] Zakładając, że ciśnienia w obu punktach są równe (\(p_1 = p_2 = p_a\)) oraz że różnica wysokości \(z_1 - z_2 = \Delta L,\) powyższe równanie upraszcza się do postaci: \[\frac{v_1^2 - v_2^2}{2g} = -\Delta L.\] Uwzględniając związek między prędkością a przepływem: \(Q = vA = v \pi d^2 / 4,\) ostateczny wzór na strumień objętościowy przyjmuje postać: \[Q = \frac{\pi d_2^2 \sqrt{2g\Delta L}}{4 \sqrt{(d_1/d_2)^4 - 1}}.\] Zatem aby wyznaczyć natężenie przepływu, wystarczy zmierzyć trzy wielkości geometryczne: średnice strumienia w dwóch przekrojach oraz odległość między tymi przekrojami. Po podstawieniu danych liczbowych otrzymujemy natężenie \(3,4\cdot 10^{-5}\mathrm{m}^3/\mathrm{s}.\)