* Redaktor Delty w roku 1974, pełniący wówczas funkcję zastępcy redaktora naczelnego.
Ile przekątnych może mieć wielościan wypukły?
Może ich nie mieć wcale. Na przykład ostrosłup nie ma przekątnych. Jeśli natomiast do jednej ściany bocznej ostrosłupa \(({n}+2)\)-kątnego tak dokleimy czworościan, aby otrzymany wielościan był wypukły i miał \(n+5\) ścian, to ten wielościan będzie miał \({n}\) przekątnych. Tak możemy w szczególności otrzymać wielościan z jedną przekątną oraz wielościan z dwiema przekątnymi.
Czy istnieją inne wielościany wypukłe z jedną przekątną? A z dwiema przekątnymi?
Wiemy, że istnieją co najmniej 3 wielościany wypukłe z jedną przekątną oraz co najmniej 8 wielościanów z dwiema przekątnymi. Poniżej podajemy ich opis. Wszystkie prezentowane wielościany otrzymujemy z graniastosłupa trójkątnego po odcięciu od niego jednego lub dwóch czworościanów.
Prawdopodobnie są to już wszystkie takie wielościany. Nie znamy dowodu, że nie ma ich więcej.
Podanie opisu wszystkich wielościanów z jedną i wszystkich wielościanów z dwiema przekątnymi wraz z dowodem, że to są rzeczywiście wszystkie takie wielościany, mogłoby być treścią ciekawej pracy, godnej zgłoszenia na Konkurs Uczniowskich Prac z Matematyki, którego 46. edycja zapowiadana jest na tylnej okładce niniejszego wydania Delty.
Wielościany wypukłe z jedną przekątną
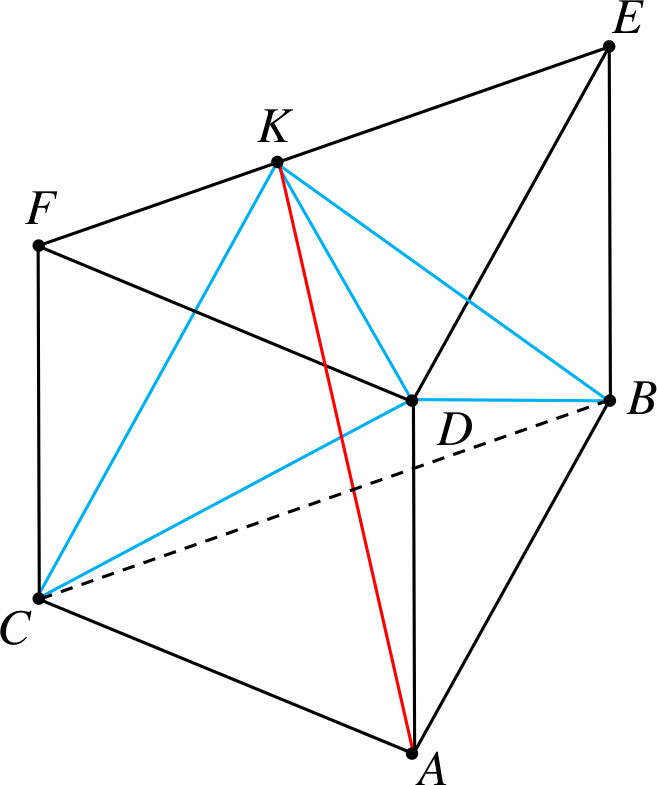
Przykład 1
Od graniastosłupa trójkątnego odcinamy
czworościany \({CDKF}\) i \({BDKE}\).
Przekątna to \({AK}\).
Uwaga: Na wielościan ten można także patrzeć jak na dwa czworościany, \({BCDA}\) i \({BCDK}\), o wspólnej ścianie \({BCD}\).
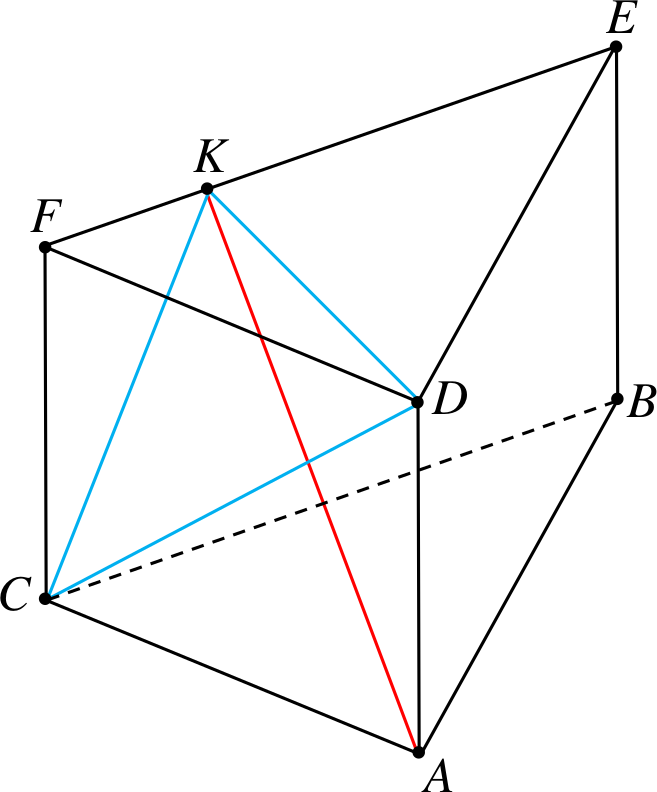
Przykład 2
Od graniastosłupa trójkątnego odcinamy
czworościan \(CDKF\).
Przekątna to \(AK\).
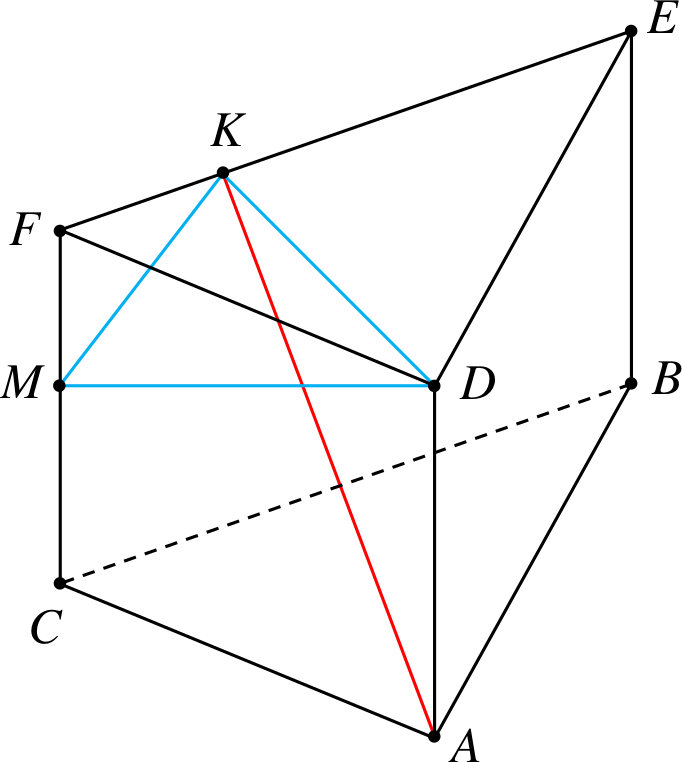
Przykład 3
Od graniastosłupa trójkątnego odcinamy
czworościan \(MDKF\).
Przekątna to \(AK\).
Przyjmujemy oznaczenia:
\(k\): liczba krawędzi wielościanu,
\(w\): liczba wierzchołków,
\(w_n\): liczba wierzchołków, w których schodzi się \(n\) krawędzi,
\(s\): liczba ścian,
\(s_n\): liczba ścian \(n\)-kątnych.
Zestawienie parametrów trzech wielościanów wypukłych z jedną przekątną.
| przykład | \(w\) | \(w_{3}\) | \(w_{4}\) | \(k\) | \(s\) | \(s_{3}\) | \(s_{4}\) | \(s_{5}\) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 2 | 3 | 9 | 6 | 6 | ||
| 2 | 6 | 4 | 2 | 10 | 6 | 4 | 2 | |
| 3 | 7 | 6 | 1 | 11 | 6 | 3 | 2 | 1 |
| ? |
Wielościany wypukłe z dwiema przekątnymi
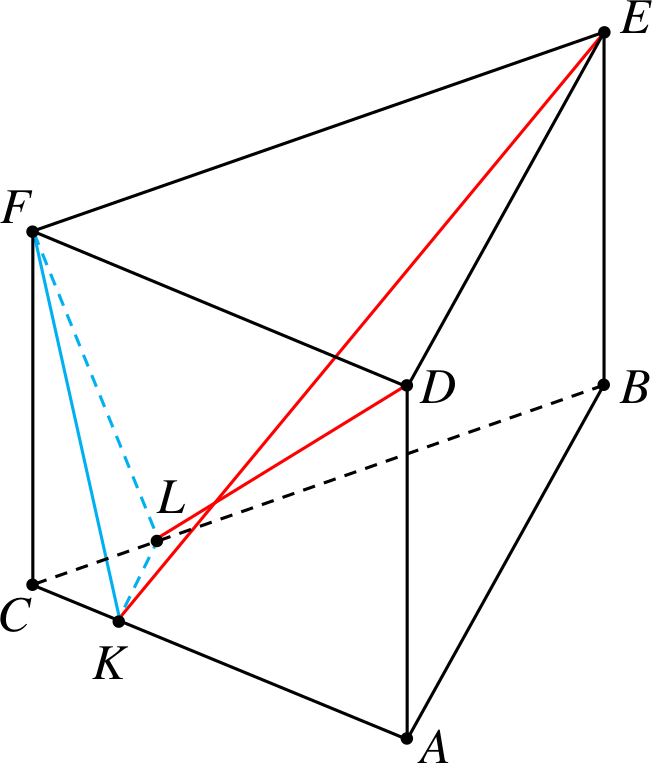
Przykład 4
Od graniastosłupa trójkątnego odcinamy
czworościan \(CKLF\).
Przekątne to \(KE\) i \(LD\).
Przykład 5
Od graniastosłupa trójkątnego odcinamy
czworościan \(CKLM\).
Przekątne to \(KE\) i \(LD\).
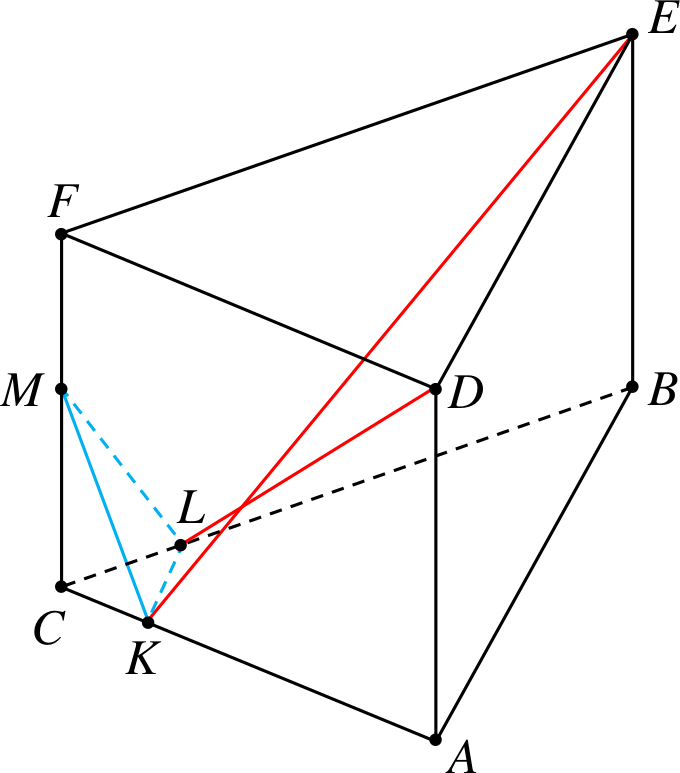
Przykład 6
Od graniastosłupa trójkątnego odcinamy
czworościany \(CALF\) i \(DBEK\).
Przekątne to \(KA\) i \(LD\).
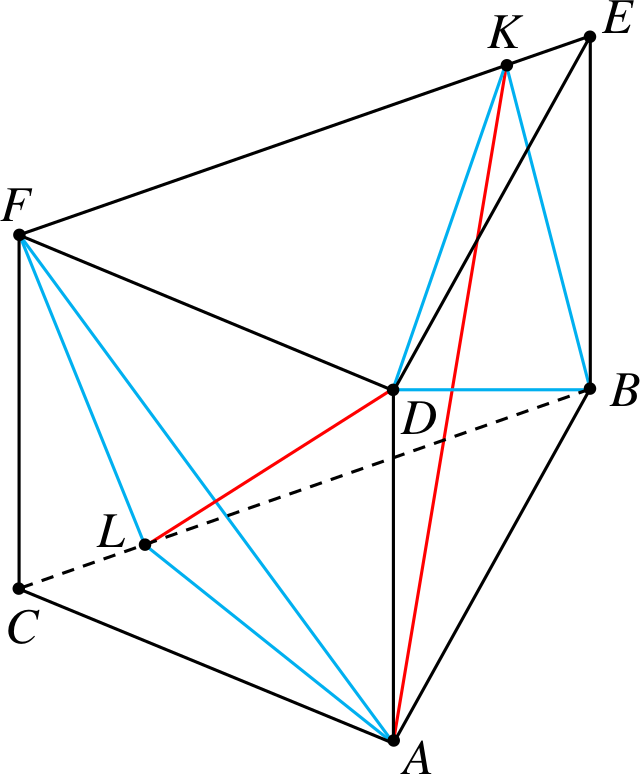
Przykład 7
Od graniastosłupa trójkątnego odcinamy
czworościany \(CALF\) i \(DMEK\).
Przekątne to \(KA\) i \(LD\).
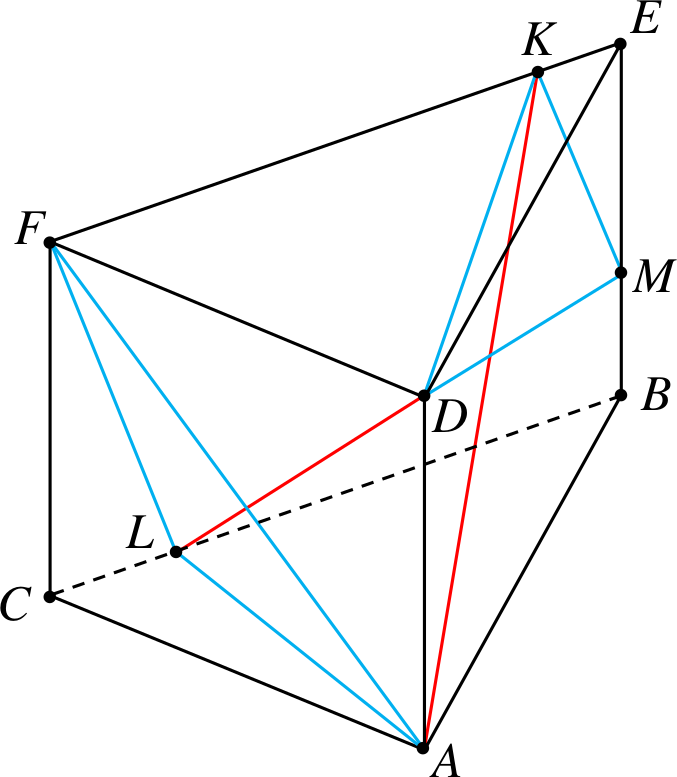
Przykład 8
Od graniastosłupa trójkątnego odcinamy
czworościany \(CALN\) i \(DMEK\).
Przekątne to \(KA\) i \(LD\).
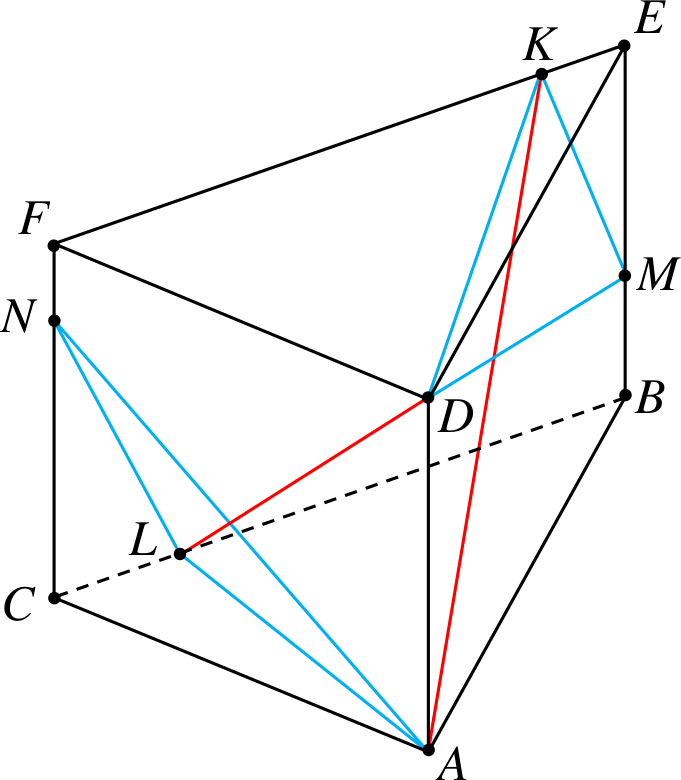
Przykład 9
Od graniastosłupa trójkątnego odcinamy
czworościany \(CDLF\) i \(DBEK\).
Przekątne to \(KA\) i \(LA\).
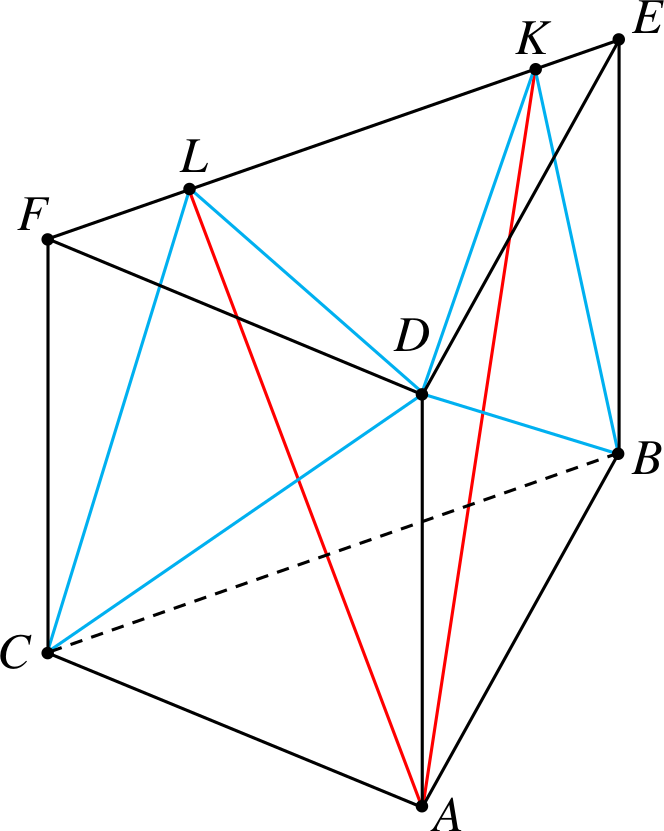
Przykład 10
Od graniastosłupa trójkątnego odcinamy
czworościany \(CDLF\) i \(DMEK\).
Przekątne to \(KA\) i \(LA\).
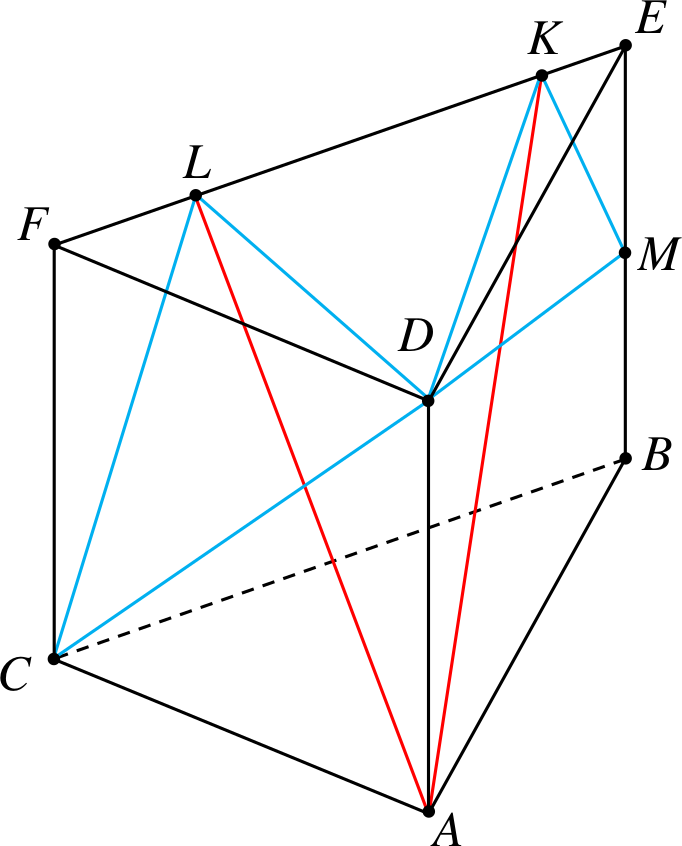
Przykład 11
Od graniastosłupa trójkątnego odcinamy
czworościany \(NDLF\) i \(DMEK\).
Przekątne to \(KA\) i \(LA\).
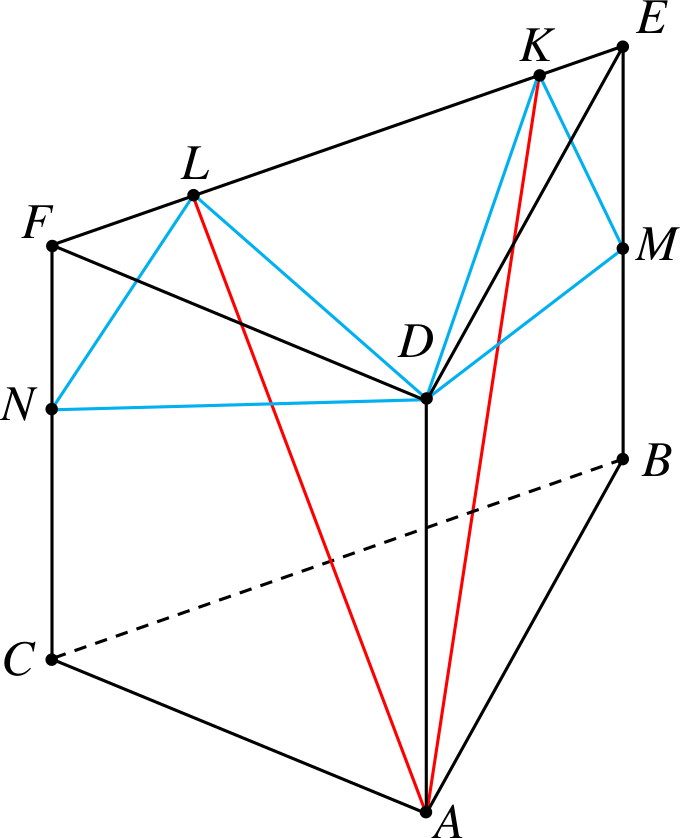
Poniżej zestawienie parametrów ośmiu wielościanów wypukłych z dwiema przekątnymi.
Typ X to taki wielościan, że dwie jego przekątne nie mają wspólnego wierzchołka, typ V to taki wielościan, że dwie jego przekątne mają wspólny wierzchołek.
| przykład | \(w\) | \(w_{3}\) | \(w_{4}\) | \(w_{5}\) | \(k\) | \(s\) | \(s_{3}\) | \(s_{4}\) | \(s_{5}\) | \(s_{6}\) | typ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 7 | 6 | 1 | 11 | 6 | 2 | 4 | X | |||
| 5 | 8 | 8 | 12 | 6 | 2 | 2 | 2 | X | |||
| 6 | 6 | 2 | 4 | 11 | 7 | 6 | 1 | X | |||
| 7 | 7 | 4 | 3 | 12 | 7 | 5 | 1 | 1 | X | ||
| 8 | 8 | 6 | 2 | 13 | 7 | 4 | 2 | 1 | X | ||
| 9 | 6 | 3 | 2 | 1 | 11 | 7 | 6 | 1 | V | ||
| 10 | 7 | 5 | 1 | 1 | 12 | 7 | 5 | 1 | 1 | V | |
| 11 | 8 | 7 | 1 | 13 | 7 | 4 | 2 | 1 | V | ||
| ? |