Babo, babo, udaj się!

…bo jak nie, to cię zjem! Od kiedy moja córeczka zaczęła odwiedzać place zabaw, a w szczególności piaskownice, regularnie słyszę to dziecinne zaklęcie.${}^{†}$ Podczas jednej ze wspólnych zabaw zdarzyło mi się bezwiednie wsypywać do odwróconych foremek suchy piasek. Ten materiał słabo nadaje się do tworzenia większych konstrukcji. Chociaż dokładałem go do oporu z każdej strony, piasek bezlitośnie przesypywał się przez krawędzie foremki i pozostawiał jedynie niewysoki kopczyk.

Zauważyłem jednak, że kształt kopczyka zależy w nieoczywisty sposób od kształtu foremki (przykłady widać na rysunkach 1–4). W okrągłej foremce naturalnie tworzył się piaskowy stożek, charakteryzujący się gładką powierzchnią z każdej strony oraz czubkiem w najwyższym punkcie. Foremka kwadratowa pozwalała utworzyć piramidę na wzór tych egipskich – ma ona cztery krawędzie zbiegające się u szczytu. W piaskownicy miałem też dostęp do imponującej wieży, której podstawą był kwadrat o zaokrąglonych kantach. Kopczyk nadal przypominał piramidę, ale jego krawędzie ,,urywały się” przed dojściem do brzegu. Dało mi to do myślenia i wypróbowałem jeszcze kilka foremek, co potwierdziło moje przypuszczenia – jeśli badana foremka miała gładki fragment brzegu, to krawędzie kopczyka tam nie sięgały.

Dlaczego tak jest? Dla weteranów piaskownic odpowiedź być może jest oczywista, dla mnie jednak nie była. Zapraszam więc Czytelnika, by razem ze mną przeszedł przez wyjaśnienie, do którego doszedłem. Okazuje się, że oprócz rozwiązania Zagadki Kanciastych Kopczyków pozwala też ono z nietypowej strony obejrzeć ciekawe zakątki analizy matematycznej.

Kopczyki a funkcja odległości. Opis kształtu kopczyka zacznijmy od podstaw: przyjmijmy, że foremka ma kształt dwuwymiarowej figury $F\subseteq {\mathbb{R}}^2,$ a powierzchnia kopczyka jest wykresem funkcji $d:F\to \mathbb{R}$ mierzącej wysokość n.p.b.f. (nad poziomem brzegu foremki). Z definicji wynika więc, że $d(\mathbf{x})=0$ dla punktów $\mathbf{x}$ leżących na brzegu foremki (oznaczanym odtąd przez $\partial F$) oraz $d(\mathbf{x})>0$ dla punktów wewnątrz. Skłonność piasku do osypywania się daje ograniczenie na to, jak stromy może być kopczyk. Dla uproszczenia przyjmiemy, że maksymalne nachylenie to ${45}^{\circ },$ a więc dowolne dwa punkty na wykresie $(\mathbf{x},d(\mathbf{x})),$ $(\mathbf{y},d(\mathbf{y}))$ są odległe w pionie nie więcej niż w poziomie. Sprowadza się to do warunku Lipschitza na funkcję $d$: $$|d(\mathbf{x})-d(\mathbf{y})|\le |\mathbf{x}-\mathbf{y}|\text{dla }\mathbf{x},\mathbf{y}\in F.$$ Funkcji spełniających te warunki jest oczywiście dużo. Nas interesuje ta, która odpowiada największemu możliwemu kopczykowi, rozpatrujemy bowiem sytuację, w której piasek dosypany w dowolnym miejscu obsypuje się poza foremkę. Do rozwiązania mamy więc problem optymalizacyjny z więzami: $$\begin{array}{c}d(\mathbf{x})=max\text{ dla }\mathbf{x}\in F\\ \text{wśród funkcji spełniających }\{\begin{array}{ll}|d(\mathbf{x})-d(\mathbf{y})|\le |\mathbf{x}-\mathbf{y}|& \text{ dla }\mathbf{x},\mathbf{y}\in F,\\ d(\mathbf{x})=0& \text{ dla }\mathbf{x}\in \partial F.\end{array}\end{array}$$ Rozwiązanie można zacząć od obserwacji, że dla $\mathbf{y}$ z brzegu i $\mathbf{x}$ dowolnego z przyjętych więzów i nierówności trójkąta wynika nierówność: $$d(\mathbf{x})\le d(\mathbf{y})+|\mathbf{x}-\mathbf{y}|=|\mathbf{x}-\mathbf{y}|.$$ Otrzymana nierówność daje najwięcej informacji, gdy $\mathbf{y}$ jest punktem brzegu najbliższym punktowi $\mathbf{x}$; możemy więc skonkludować, że $d(\mathbf{x})$ nie przewyższa $min\{|\mathbf{x}-\mathbf{y}|:\mathbf{y}\in \partial F\}.$ Tę ostatnią wielkość nazwiemy odległością $\mathbf{x}$ od brzegu i oznaczymy przez $d_{\partial F}(\mathbf{x}).$

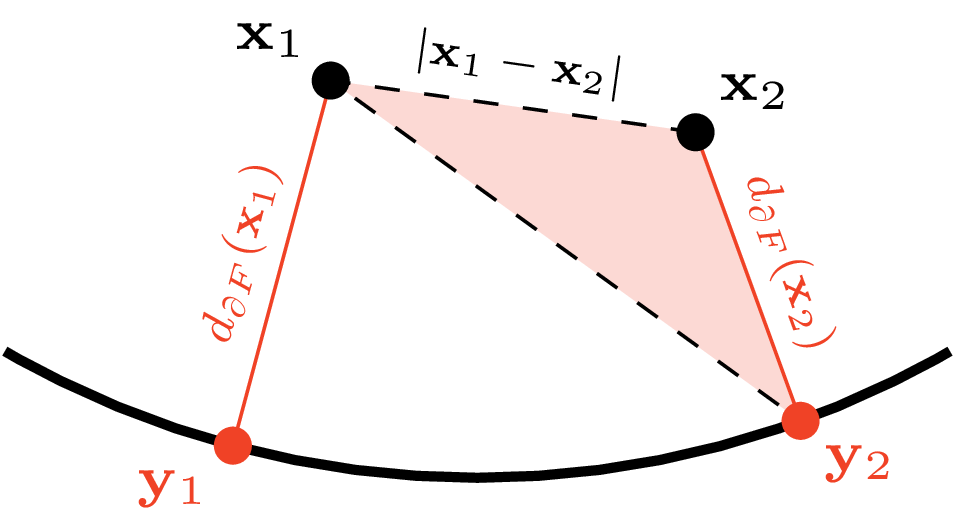
Pozostaje sprawdzić, że funkcja $d_{\partial F}$ również spełnia nałożone ograniczenia – wówczas będziemy mieli pewność, że to właśnie jest szukana funkcja odpowiadająca największemu możliwemu kopczykowi. Warunek $d(\mathbf{x})=0$ dla $\mathbf{x}$ z brzegu jest spełniony automatycznie, gdyż minimum jest przyjmowane dla $\mathbf{y}=\mathbf{x}.$ Natomiast jeśli dane są dwa punkty ${\mathbf{x}}_1,{\mathbf{x}}_2\in F$ oraz najbliższe im punkty ${\mathbf{y}}_1,{\mathbf{y}}_2\in \partial F$ (jak na rys. 5), to z nierówności trójkąta mamy: $$\underset{d_{\partial F}({\mathbf{x}}_1)}{\underbrace{|{\mathbf{x}}_1-{\mathbf{y}}_1|}}\le |{\mathbf{x}}_1-{\mathbf{y}}_2|\le |{\mathbf{x}}_1-{\mathbf{x}}_2|+\underset{d_{\partial F}({\mathbf{x}}_2)}{\underbrace{|{\mathbf{x}}_2-{\mathbf{y}}_2|}},$$ a więc $d_{\partial F}({\mathbf{x}}_1)-d_{\partial F}({\mathbf{x}}_2)\le |{\mathbf{x}}_1-{\mathbf{x}}_2|.$ Po połączeniu z analogiczną nierównością, w której ${\mathbf{x}}_1,{\mathbf{x}}_2$ są zamienione miejscami, daje to warunek Lipschitza dla $d_{\partial F}.$ Wniosek: szukaną funkcją $d$ jest $d_{\partial F}.$

Krawędzie kopczyków w języku analizy. Okazuje się, że analiza matematyczna dysponuje właściwym językiem do opisu gładkich i niegładkich fragmentów kopczyków – kluczem jest tu pojęcie różniczkowalności funkcji $d.$ Zacznijmy od obserwacji, że cechą odróżniającą gładkie fragmenty od krawędzi i wierzchołków jest możliwość określenia płaszczyzny stycznej (przydatna, gdy zdecydujemy się ozdabiać kopczyk fragmentami muszelek). Ogólne równanie na płaszczyznę przechodzącą przez wybrany punkt wykresu $(x_1,x_2,d(x_1,x_2))$ to: $$(z_1,z_2,z_3):z_3=d(x_1,x_2)+a_1\cdot (z_1-x_1)+a_2\cdot (z_2-x_2),$$ natomiast płaszczyznę taką nazywamy styczną, gdy dobrze przybliża ona wykres funkcji $d,$ a więc gdy $z_3$ wyliczone ze wzoru wyżej jest blisko wartości $d(z_1,z_2).$ Warunek ten można ściśle sformułować poprzez zbieżność: $$\begin{array}{}\text{(}\star \text{)}& \frac{d(x_1,x_2)+a_1\cdot (z_1-x_1)+a_2\cdot (z_2-x_2)-d(z_1,z_2)}{\sqrt{(z_1-x_1{)}^2+(z_2-x_2{)}^2}}⟶0\end{array}$$ przy $(z_1,z_2)\to (x_1,x_2).$

Czytelnik mający za sobą kurs analizy matematycznej wielu zmiennych rozpozna w powyższym warunku definicję różniczkowalności. Konkretnie, funkcję $d$ uznajemy za różniczkowalną w punkcie $(x_1,x_2),$ jeśli istnieją liczby $a_1,a_2$ spełniające warunek $\text{(}\star \text{)}$. Pojęcie różniczkowalności jest kluczowe dla tej dziedziny i wypada poświęcić mu kilka słów, ale pozostawmy je na marginesie obok.

Dla wyrobienia lepszej intuicji wróćmy na chwilę do rysunku 2. Jeśli przyjmiemy, że kwadrat na rysunku to zbiór zadany nierównościami $|x_1|,|x_2|\le 1,$ to funkcja odległości od brzegu $d$ jest dana wzorem $1\pm x_{1,2},$ zależnie od części kwadratu. Na przykład w trójkącie zadanym przez $-x_1\le x_2\le x_1$ mamy $d(x_1,x_2)=1-x_1,$ a więc sama funkcja $d$ jest liniowa! Nie jest więc zaskakujące, że w każdym punkcie wewnętrznym tego trójkąta para $a_1=-1,$ $a_2=0$ spełnia warunek $\text{(}\star \text{)}$ – po prostu licznik się zeruje dla $\mathbf{z}$ dostatecznie bliskich $\mathbf{x}.$ Z kolei w punktach leżących na przekątnych $(x_1=\pm x_2)$ par $a_1,a_2$ spełniających $\text{(}\star \text{)}$ po prostu nie ma.

Zagadka Kanciastych Kopczyków. Wyjaśnienie zagadki opiera się na następującym twierdzeniu, które tutaj przytoczymy bez dowodu:

Twierdzenie. Jeśli $C\subseteq {\mathbb{R}}^2$ jest gładką zamkniętą krzywą, to funkcja odległości $d_C$ jest różniczkowalna w każdym punkcie $r$-otoczki $C,$ czyli zbioru $$C_r:=\{\mathbf{x}\in {\mathbb{R}}^2:|\mathbf{x}-\mathbf{y}|<r\text{ dla pewnego }\mathbf{y}\in C\},$$ o ile $r>0$ jest odpowiednio małe (mniejsze od odwrotności krzywizny w każdym punkcie $C).$)

Jest to szczególny przypadek twierdzenia o otoczeniu tubularnym, które stali Czytelnicy Delty mogą znać z artykułu o obwarzankach w ${\mathrm{\Delta }}_{22}^9$. W naszym przypadku wystarczy za krzywą $C$ przyjąć brzeg $\partial F,$ by przekonać się, że gładki brzeg gwarantuje różniczkowalność $d$ w pewnym otoczeniu $\partial F,$ a więc krawędzie (składające się z punktów nieróżniczkowalności) do tego brzegu nie mogą dochodzić. Jest możliwa nawet bardziej ilościowa analiza: jeśli na rysunku 3 przyjmiemy, że zaokrąglone kanty to łuki okręgu o promieniu $r,$ to krzywizna brzegu jest ograniczona z góry przez $1/r.$ I rzeczywiście, krawędzie kończą się dokładnie w odległości $r$ od brzegu.

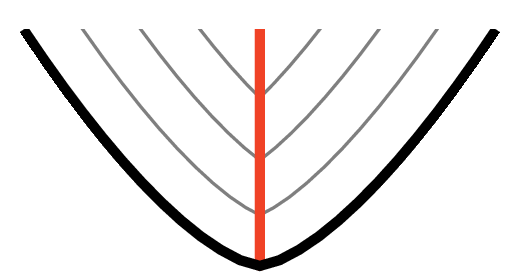
Co dalej? Dalsza zabawa piaskiem prowadzi do wniosku, że sytuacja jest jeszcze ciekawsza. Są kształty, jak na rysunku 6, gdzie foremka ma kant, ale kopczyk jest gładki mimo to. Kluczowe jest tutaj, że kant jest skierowany do wewnątrz; powoduje on, że funkcja odległości nie jest różniczkowalna na zewnątrz foremki, ale tego już nie widzimy. Podobny efekt uzyskamy, jeśli nasypiemy sobie piasku na stopę.

Są też foremki jak ta na rysunku 7, która wydaje się gładka, ale kopczyk ma krawędź aż do brzegu. Tu diabeł tkwi w szczegółach – okazuje się, że brzeg foremki nie jest dostatecznie gładki. Owszem, ma wszędzie określoną prostą styczną, ale jego krzywizna jest nieograniczona. W języku analizy: funkcja $|x{|}^{3/2}$ jest rożniczkowalna, ale tylko raz, a dwukrotnie już nie.

Wreszcie, ciekawy jest przypadek, gdy usypujemy kopczyk na zewnątrz foremki – w następnym numerze ukaże się artykuł Sławomira Dinewa poświęcony temu zagadnieniu. Trudno sobie wyobrazić, jak taki kopczyk wykonać w piaskownicy – na plaży być może byłaby szansa – ale sam problem okazuje się całkiem bogaty od strony czysto matematycznej. Foremki, dla których ,,zewnętrzne kopczyki” są gładkie, całkowicie charakteryzuje twierdzenie Motzkina… ale o tym za miesiąc!