Afiliacja: Instytut Fizyki PAN
W artykule \(\Delta^{4}_{22}\) pisałem o interwałach i rachowaniu na nich, czyli analizie interwałowej (przedziałowej). Niniejszy esej ma na celu zbadanie użyteczności metod analizy interwałowej do rozwiązywania dowolnych równań algebraicznych, względnie układów takich równań.
Matematycy od dawna zajmowali się sposobami rozwiązywania równań. Znaleziono na przykład wzory na pierwiastki równań kwadratowych, wielomianowych trzeciego i czwartego stopnia – ale nie wyższego. Jednak skoro nie da się rozwiązać danego równania analitycznie, to konieczne staje się użycie metod numerycznych. Powstały więc całkiem liczne algorytmy pozwalające znajdować dobre przybliżenia poszukiwanych pierwiastków. Można tu wymienić metodę znaną pod łacińską nazwą regula falsi czy szybciej zbieżną metodę Newtona. Problem w tym, że rozwiązanie równania polega na znalezieniu wszystkich jego pierwiastków lub wykazaniu, że takowe nie istnieją. Tymczasem wynik metody Newtona zależy od wyboru pierwszego przybliżenia (punktu startowego), a bywa, że procedura okazuje się rozbieżna. Co więcej, nawet jeśli uzyskamy zbieżność, to do jednego rozwiązania – bez żadnych wskazówek, czy jest ono jedyne.
Tu proponujemy metodę opartą na prostym spostrzeżeniu. Otóż jeśli potrafimy obliczyć przedziały wartości lewej \((L)\) i prawej \((P)\) strony naszego równania \(L(x) = P(x)\) dla badanego przedziału wartości poszukiwanej niewiadomej \(x\) i część wspólna owych dwóch przedziałów okaże się zbiorem pustym, to w badanym przedziale \(x\) z całą pewnością nie ma rozwiązania. Oczywiście w przeciwnym wypadku nie mamy gwarancji, że testowany przedział \(x\) zawiera choć jedno rozwiązanie. O tym, jak wyliczamy wspomniane przedziały \(L(x)\) i \(P(x)\) w przypadku, gdy są to jakieś wyrażenia algebraiczne, lub nawet bardziej skomplikowane funkcje, pisaliśmy w \(\Delta^{4}_{22}\).
Na początku startujemy z przedziału, w którym spodziewamy się
znaleźć rozwiązanie. Jeśli nasze informacje (czy przypuszczenia)
co do lokalizacji rozwiązania są mało precyzyjne, to nie ma
przeszkód, aby przedział startowy powiększyć.
Będziemy pracować na liście przedziałów \(\mathcal{L},\) której
początkowo jedynym elementem będzie nasz
przedział startowy. Poza tym musimy jeszcze zdefiniować
dokładność \(\varepsilon,\) z jaką chcemy znaleźć poszukiwany
pierwiastek (pierwiastki). Ciąg dalszy jest prosty.
Pierwszy etap:
Jeśli lista \(\mathcal{L}\) jest pusta, to przechodzimy do drugiego etapu.
Pobieramy najszerszy przedział z listy \(\mathcal{L}.\) Jeśli jego szerokość nie przewyższa \(\varepsilon,\) to przechodzimy do drugiego etapu. W przeciwnym razie usuwamy pobrany element z listy \(\mathcal{L}.\)
Pobrany przedział dzielimy na dwie połówki i zaokrąglamy górną granicę lewego podprzedziału w górę, a dolną granicę prawego w dół.
Wykonujemy wcześniej opisany test na obecność rozwiązania kolejno na obu podprzedziałach. Jeśli test nie wyklucza obecności rozwiązania, to dany podprzedział dopisujemy do listy \(\mathcal{L}\); w przeciwnym razie testowany podprzedział idzie w zapomnienie.
Wracamy do punktu 1.
Drugi etap:
Jeśli lista \(\mathcal{L}\) jest pusta, to znaczy, że w startowym
przedziale badane równanie nie ma żadnego rozwiązania.
Ta wiadomość jest pewna, choć zapewne nie na taką liczyliśmy.
Jeśli jednak lista \(\mathcal{L}\) zawiera więcej niż jeden element,
to mamy co robić. Trzeba mianowicie wykryć wszystkie grupy
przedziałów wzajemnie przekrywających się (to możliwe,
bo przecież zaokrąglaliśmy granice podziałów!). A już na pewno
tak się zdarzy, jeśli nasze równanie ma kilka różnych rozwiązań
zlokalizowanych w przedziale startowym. Możliwe jednak, że
nawet w przypadku pojedynczego rozwiązania na liście
\(\mathcal{L}\) pozostanie nam więcej niż jeden przedział.
Jako wynik końcowy wypisujemy powłoki wypukłe (patrz dalej)
kompletnych grup wzajemnie połączonych małych przedziałów.
A jak poradzimy sobie z układem kilku równań? Właściwie tak samo jak z pojedynczym równaniem. Różnica polega na tym, że zamiast przedziałów na osi liczbowej testujemy wielowymiarowe kostki interwałowe opisujące zakresy wszystkich poszukiwanych niewiadomych. W literaturze takie obiekty zwykle nazywane są kostkami lub pudełkami. Kostka odpada z dalszych rozważań, jeśli choć jedno równanie na pewno nie może być w niej spełnione. No dobrze, ale która kostka na liście \(\mathcal{L}\) jest największa, czyli pierwsza w kolejności do testowania? To proste: ta o największej średnicy. A średnica interwałowej kostki jest zdefiniowana jako długość jej najdłuższej krawędzi. Tylko jak porównać długości krawędzi wyrażonych w różnych jednostkach fizycznych, np. jedna w sekundach, a druga w metrach? Sposób jest nieskomplikowany: mierzymy te długości w ustalonych wcześniej żądanych dokładnościach, czyli posługujemy się wielkościami bezwymiarowymi.
No dobrze, ale jak podana metoda działa w praktyce?
Wikipedia (\(\tt{en.wikipedia.org/wiki/Regula\_falsi},\) ostatnio aktualizowana 26 listopada 2022 r.) podaje rozwiązanie równania \(\cos(x) = x^{3}\) jako: \(x = 0,865~474~033~101~614\) z dokładnością \(5\times 10^{-15}.\) Tymczasem nasza metoda, z nieco gorszą dokładnością \(\varepsilon=10^{-14},\) wyprodukowała interwał: \([ 0,865~474~033~101~523, ~0,865~474~033~101~690 ]\) (startując z przedziału \([0,~1]\)). Otrzymaliśmy ten wynik po przeanalizowaniu \(356\) przedziałów. W drugim etapie okazało się, że \(45\) ,,małych” przedziałów tworzy pojedynczą grupę. Wynik końcowy otrzymaliśmy po \(4\) milisekundach. Jak widać, nie osiągnęliśmy żądanej dokładności, ale jednocześnie widzimy, że wynik z Wikipedii mieści się w naszym (gwarantowanym) przedziale. A nie próbowaliśmy powtórzyć wyniku z Wikipedii? Owszem, próbowaliśmy, ale w pierwszym podejściu skończyła nam się pamięć przeznaczona na listę \(\mathcal{L}.\) Kiedy zarezerwowaliśmy na listę \(\mathcal{L}\) dużo więcej, bo \(4~096~000\) pozycji, to i tak okazało się za mało, a czas obliczeń wyniósł \(155~231\) sekund, czyli ponad \(43\) godziny! Wszystkie ,,małe” przedziały tworzyły pojedynczą grupę o sumarycznym rozmiarze tylko nieznacznie mniejszym od tego otrzymanego przy raptem dwukrotnie gorszej dokładności. Cóż to znaczy? Ano tyle, że wynik podziału niewielkiego przedziału (po niezbędnych zaokrągleniach) to dwa nowe przedziały praktycznie identyczne z wyjściowym. W każdym razie warto zapamiętać, że komputerowe liczby podwójnej precyzji zawierają co najwyżej \(13\) poprawnych dziesiętnych cyfr znaczących, a nie \(15\)–\(16,\) jak podają niektórzy autorzy.
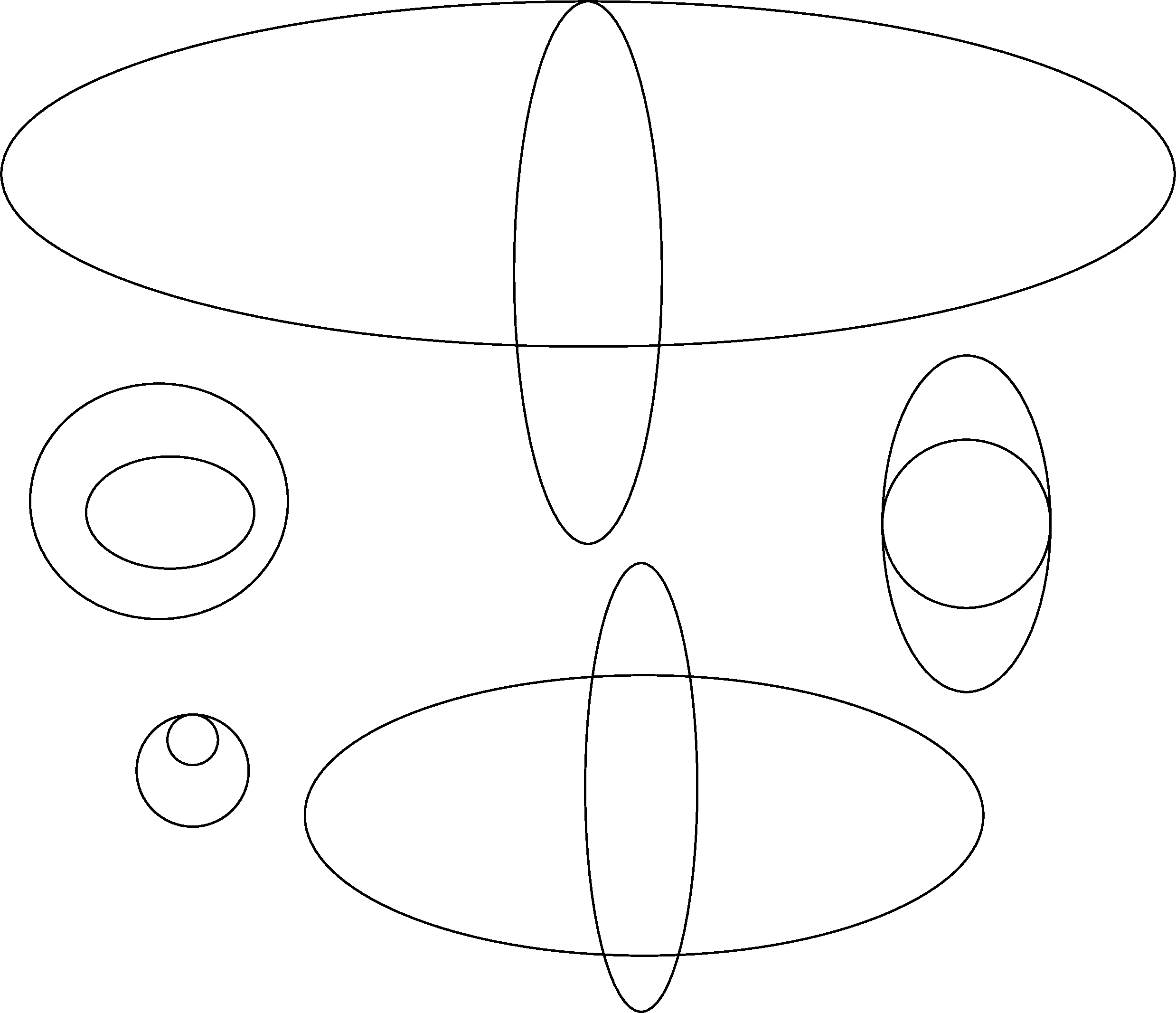
Eksperymenty z układami dwóch równań, każde oddzielnie opisujące elipsę (patrz rysunek), okazały się jeszcze bardziej zaskakujące. O ile przypadki zawierające 0, 1, 2 czy 4 rozwiązania były łatwe, to 3 rozwiązania (patrz rysunek) okazały się kłopotliwe. Nie dość, że zabrakło miejsca na liście \(\mathcal{L}\) (ponad 2 miliony pozycji), to znaleźliśmy na niej 7 rozłącznych grup, każda zawierająca prawie 300 tysięcy kostek. Dalsza analiza każdej z tych grup oddzielnie wykazała, że cztery z nich na pewno nie zawierają żadnego rozwiązania.
Dwie elipsy mogą mieć 0, 1, 2, 3 lub 4 punkty wspólne
Wady i zalety
Niewątpliwą zaletą jest znalezienie wszystkich rozwiązań w rozważanym
przedziale. Ale bądźmy szczerzy: to nie są rozwiązania, a jedynie kandydaci
na rozwiązania. Nie możemy też mieć pewności, że konkretna grupa
połączonych przedziałów zawiera tylko jednego takiego kandydata.
Z drugiej strony metoda jest uniwersalna, gdyż nie wymaga, aby funkcje
występujące po obu stronach równania były gładkie (różniczkowalne).
A nawet mogą być nieciągłe. Trudno jest też rzetelnie przewidzieć
złożoność obliczeniową prezentowanej metody.
Z pewnością w pierwszym podejściu nie warto upierać się przy zbyt dużej dokładności.