Afiliacja: CWI, Amsterdam i Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
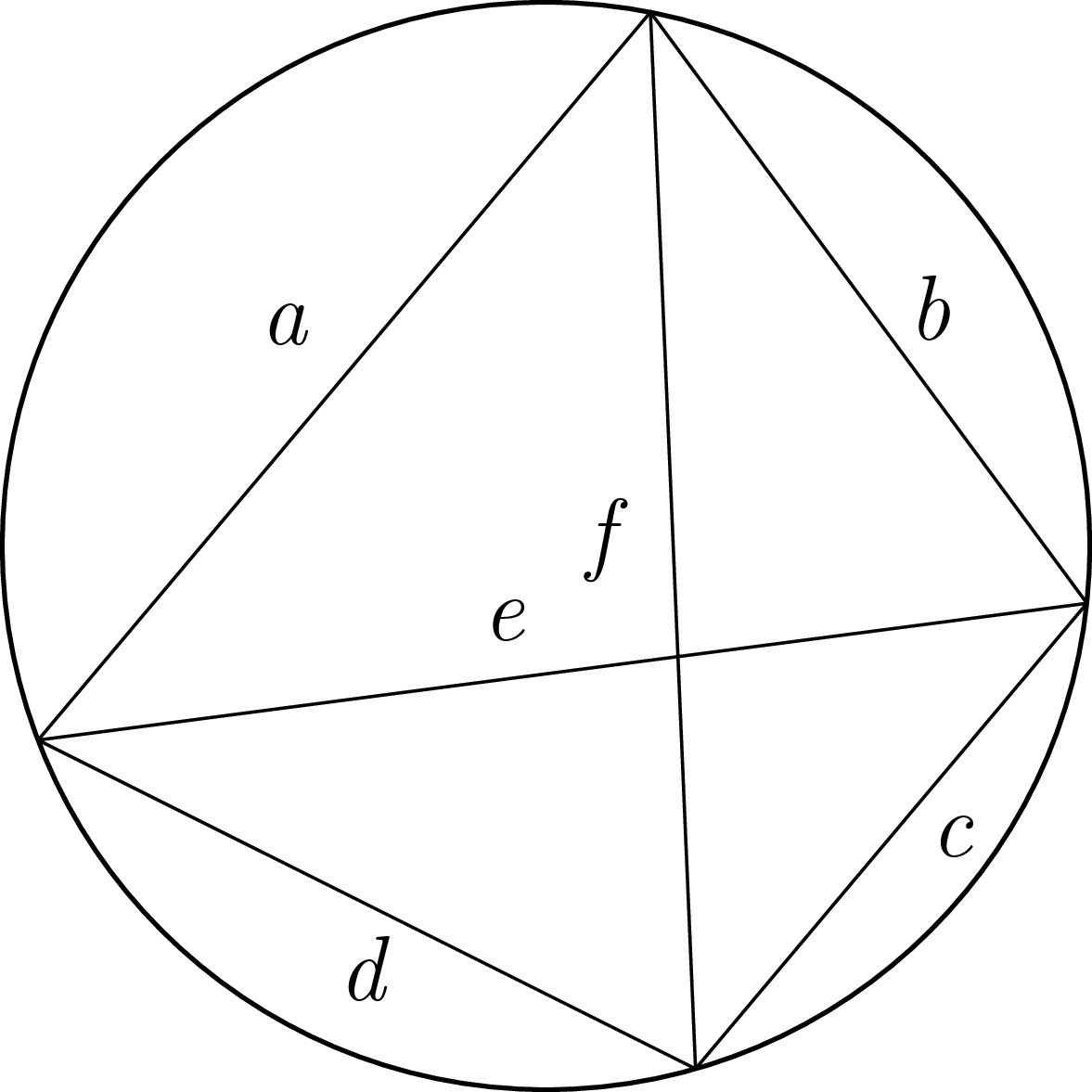
Twierdzenie Ptolemeusza: \(ac+bd=ef.\)
Twierdzenie Ptolemeusza, udowodnione przez Klaudiusza Ptolemeusza (100 – około 168), ma następującą postać:
W czworokącie wpisanym w okrąg iloczyn długości przekątnych jest równy sumie iloczynów długości przeciwległych boków (patrz rysunek na marginesie).
Twierdzenie to ma wiele znanych dowodów, niektóre z nich można znaleźć w Wikipedii. Celem tej notki jest zaprezentowanie pięknego dowodu, autorstwa W. Derricka i J. Hersteina, który został przedstawiony jako ,,dowód bez słów”, zawierający jedynie dwa z poniższych rysunków: pierwszy i trzeci. Aby wyjaśnić szczegóły, dodaliśmy jeszcze jeden rysunek.
W. Derrick and J. Herstein, Proof without words: Ptolemy’s theorem, The College Mathematics Journal, 43(5), p. 386, November 2012.
Dowód ten został spopularyzowany przez stronę A. Bogomolny, https://www.cut-the-knot.org/.
W dowodzie wykorzystujemy następujące twierdzenie.
Twierdzenie. Kąty wpisane w okrąg oparte na tej samej cięciwie są równe.
Oznaczmy kąty jak na
rysunku poniżej. Podwójne wystąpienia \(\alpha, \beta, \gamma\) i \(\delta\) są uzasadnione przez powyższe twierdzenie.
Na przykład oba kąty wpisane oznaczone przez \(\alpha\) są oparte na boku długości \(a.\)
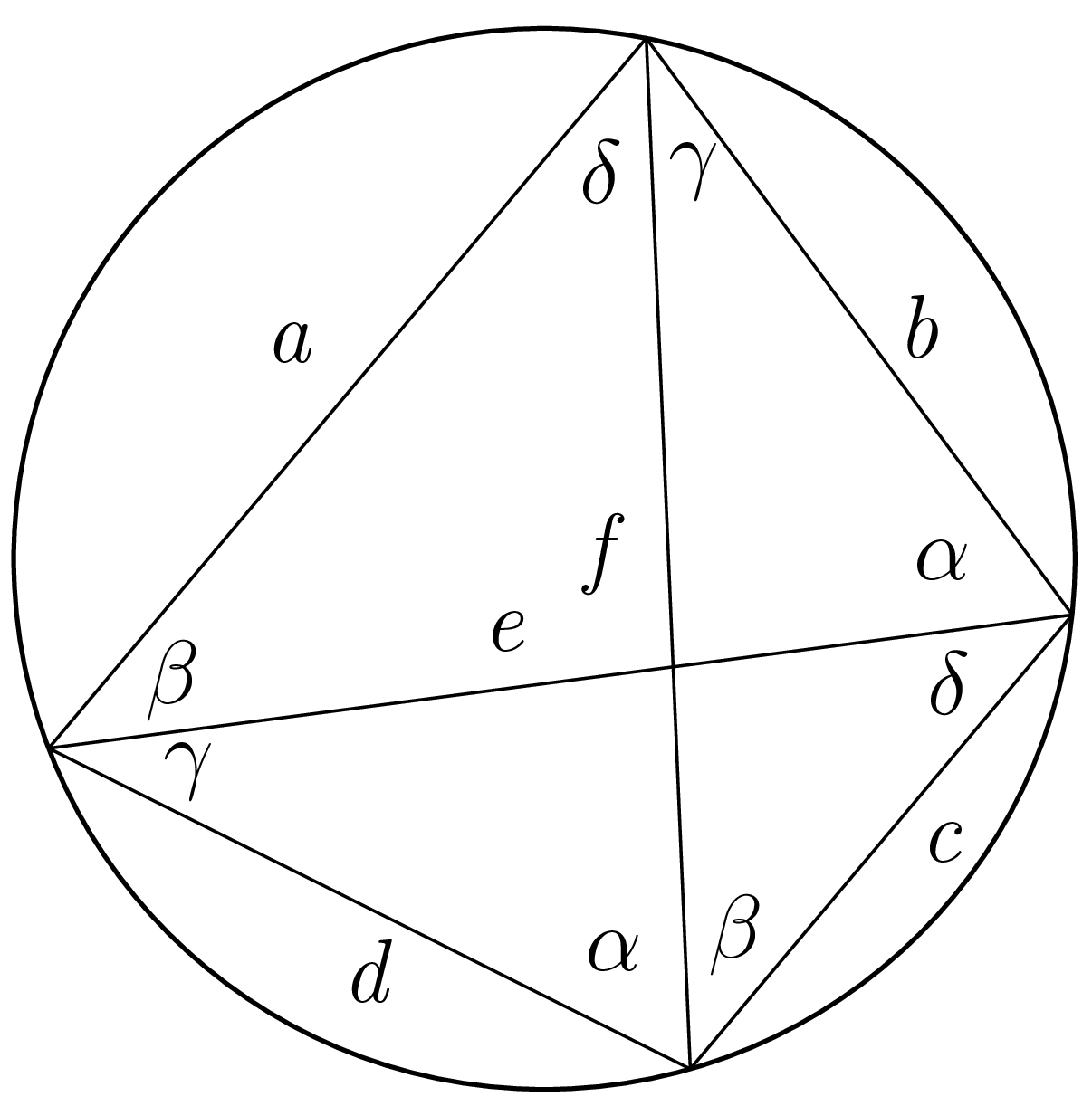
Aby udowodnić twierdzenie Ptolemeusza, wybierzemy teraz z oryginalnego rysunku trzy trójkąty, które odpowiednio obrócimy.
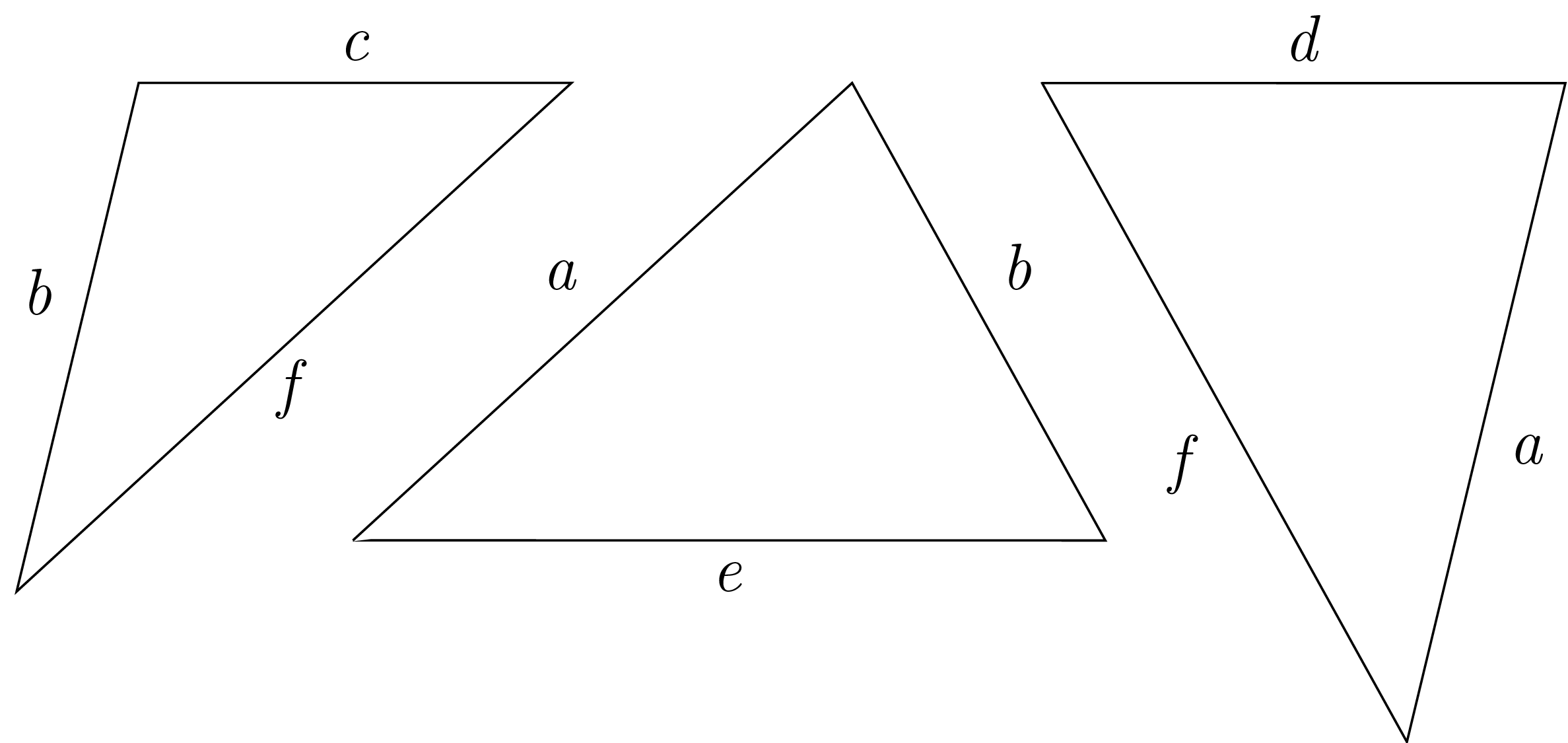
Następnie przeskalujemy je odpowiednio przez \(a,\) \(f\) i \(b,\) aby mogły być ułożone obok siebie i aby utworzyć poniższy rysunek, w którym ponownie wykorzystujemy oryginalne oznaczenia kątów.
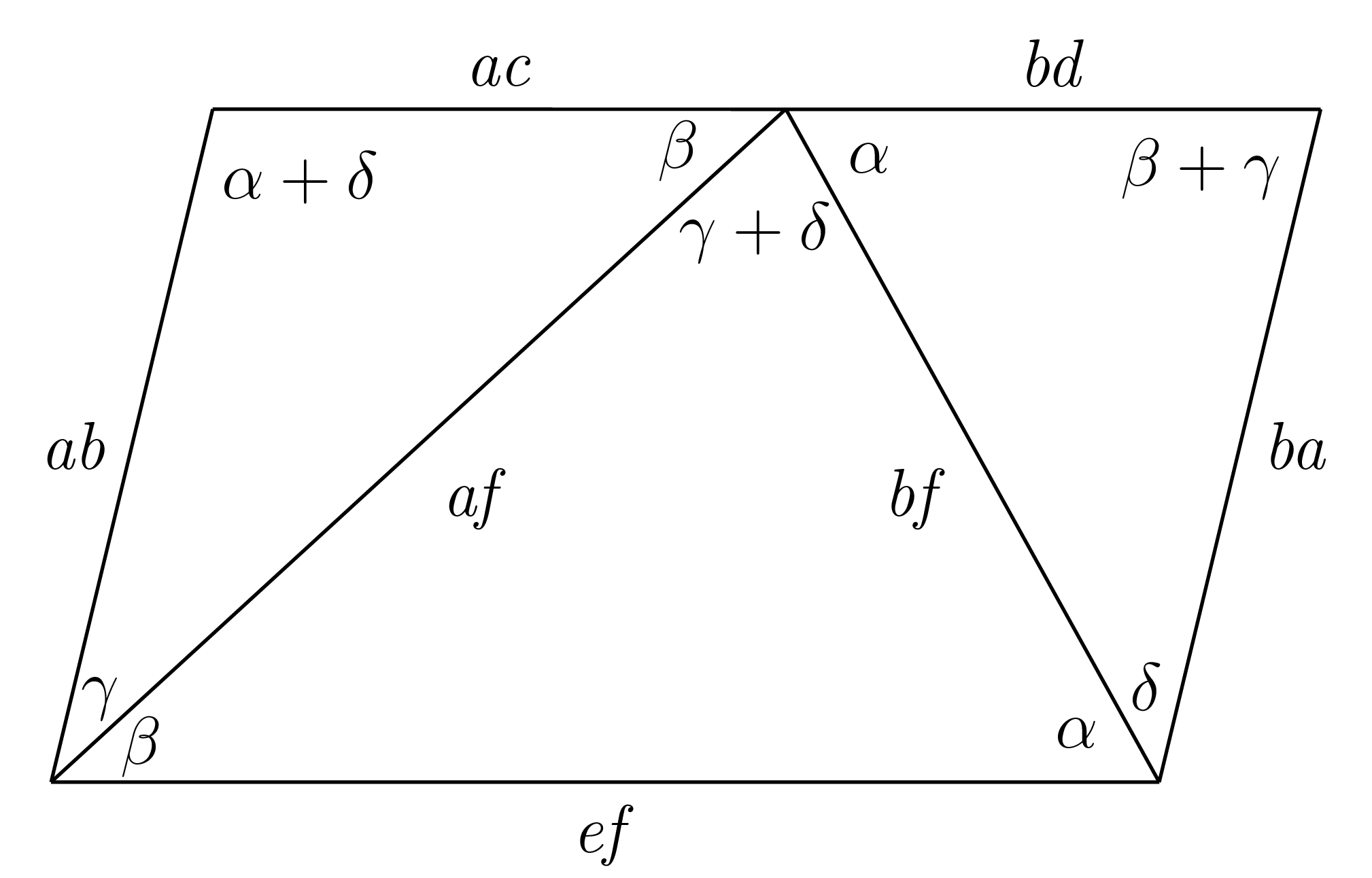
Zauważmy, że \(ac\) i \(bd\) leżą na tej samej linii, ponieważ \(\beta + \gamma + \delta + \alpha = 180^{\circ},\) co wynika z tego, że suma kątów oryginalnego czworokąta to \(2 (\alpha + \beta + \gamma + \delta) = 360^{\circ}.\) Zatem powyższy rysunek przedstawia czworokąt.
Oznaczenia kątów również ujawniają, że pary przeciwległych kątów czworokąta są równe: oba są równe \(\alpha + \delta\) lub \(\beta + \gamma.\) Zatem ten czworokąt jest równoległobokiem. Jego przeciwległe boki są równej długości, zatem \(ac + bd = ef.\)
Ciekawą, prostą konsekwencją tego twierdzenia jest następująca obserwacja.
Twierdzenie. W pięciokącie foremnym z bokami o długości \(a\) i przekątnymi o długości \(b,\) zachodzi \(\frac{b}{a} = \phi,\) gdzie \(\phi = \frac{1+\sqrt{5}}{2}\) jest tzw. złotą liczbą.
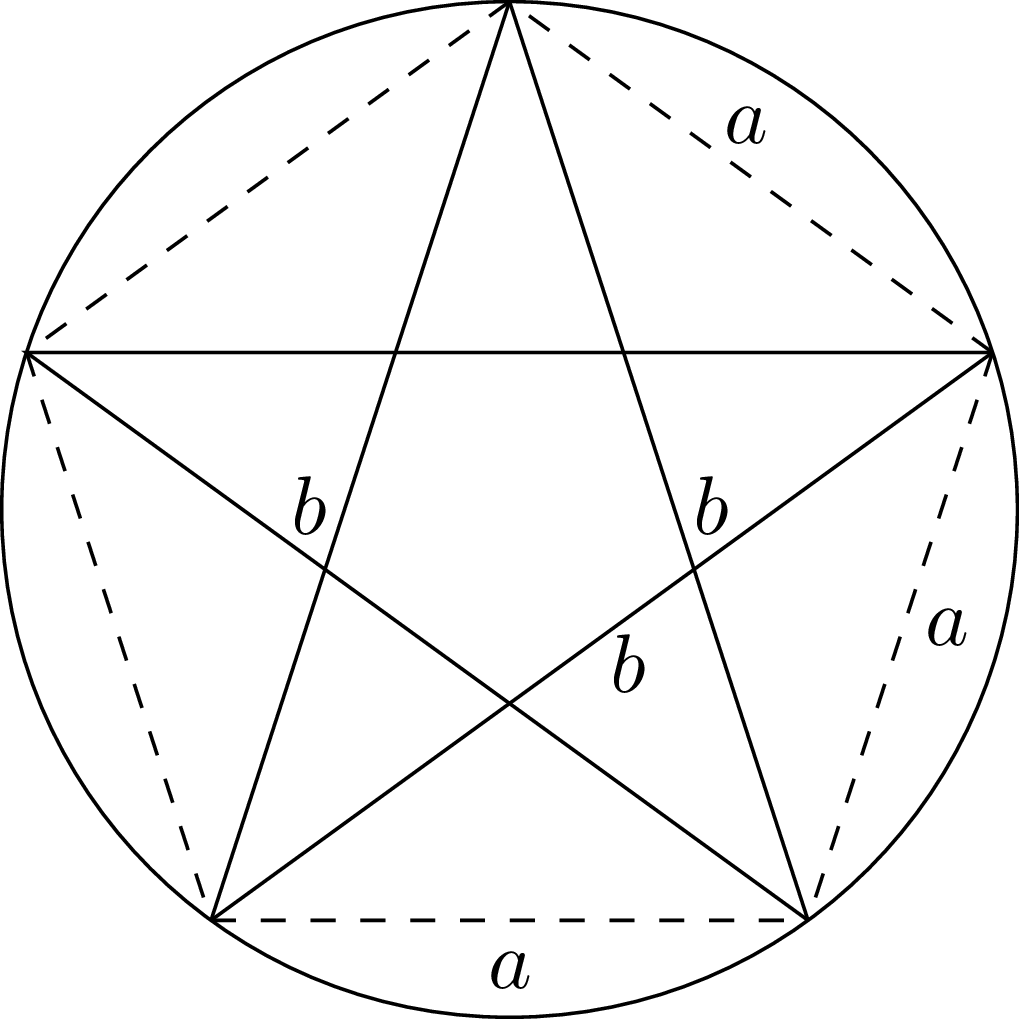
Aby udowodnić to twierdzenie, przypomnijmy, że złota liczba \(\phi\) spełnia równanie \(1 + \phi = \phi^2,\) i rozważmy czworokąt z bokami \(a, a, a,\) i \(b\) (z przekątnymi \(b\) i \(b\)). Z twierdzenia Ptolemeusza \(a^2 + ab = b^2.\) Dzieląc obie strony przez \(a^2,\) otrzymujemy równanie: \[1 + \frac{b}{a} = \bigg{(}\frac{b}{a}\bigg{)}^2.\] To oznacza, że \(\frac{b}{a}\) spełnia to samo równanie co złota liczba. Ponieważ to równanie kwadratowe ma tylko jedno dodatnie rozwiązanie, zachodzi \(\frac{b}{a} = \phi.\)
Tekst oparty na załączniku 7 z książki: Krzysztof R. Apt, “A Brief History of Mathematics for Curious Minds”, World Scientific, 2024. Rysunki zostały stworzone przez Magdalenę Kycler i Piotra Sitka.